基于模型优化的广义自由表面多次波压制技术在印度洋深水海域的应用

王小杰，颜中辉，刘俊，刘欣欣，杨佳佳

1. 中国地质调查局青岛海洋地质研究所，青岛 266237

2. 青岛海洋科学与技术试点国家实验室海洋矿产资源评价与探测技术功能实验室，青岛 266237

1 研究背景

在海洋资料中，多次波干扰非常发育并且种类也较多，有海水的鸣震、强海底尤其是崎岖海底产生的海底相关多次波、强反射界面产生的层间和长周期多次波等，这些多次波会造成地震记录中有效反射能量被压制，信噪比降低。因此，多次波的压制一直是海洋地震数据处理中的难点问题，也是海上资料处理的主要任务[1]。

深水海域地震资料数据处理是深水油气勘探的重要环节，其中多次波的压制又是重中之重，它直接影响到地震资料的品质，因此在偏移之前，尽可能地压制或衰减多次波。在深水海域，存在的多次波主要是自由表面多次波，该类多次波定义为地下介质反射的地震波到达自由表面后，至少发生一次下行反射，然后经一定传播路径后重新返回自由表面所接收的地震波[2-3]。可以说，在深水海域，如果能够压制自由表面多次波，也就压制了大部分的多次波干扰，因此自由表面多次波的压制是整个多次波压制的重点。针对此类多次波，学者们提出了很多压制的方法，有CMP叠加、f-k滤波法、Radon变换、聚束滤波法、预测反褶积和基于波动理论的多次波预测相减法等，其中目前最为广泛应用的是广义自由表面多次波预测技术（General-Surface Multiple Prediction，GSMP），相比于传统的二维自由表面多次波压制技术（Surface-Related Multiple Elimination，SRME），该技术预测的多次波模型更准确。同时，海上二维采集过程中电缆中—远偏移距难免受海流影响而偏离设计测线方向形成羽角，这是海上二维地震资料采集的固有特点。羽角的存在使共反射点发散无法满足SRME技术对规则化采集的要求，从而影响后续的多次波预测。因此，在本次多次波压制中，我们采用的是GSMP技术，但是在印度洋深水海域，海底相关多次波能量强，频带宽，常规的GSMP技术也不能得到很好的压制，因此，本文利用曲波变换，将多次波模型进一步优化，得到更加精确的多次波模型，从而使多次波的压制效果更好[4-9]。

2 方法原理

2.1 广义自由表面多次波预测技术

广义自由表面多次波预测技术是近几年来逐渐兴起并广泛应用于海洋地震资料数据处理中的一项新技术。在理论上，该技术可以预测并衰减所有与地表相关的多次波，并且无需地下任何的先验信息，如速度、地层和构造等信息，是基于数据驱动的。广义自由表面多次波预测是通过模型建立和自适应减去法实现的，具体的实现途径为波动方程建模法，是在地表一致性褶积法的基础上进行改进的，通过波动方程外推来实现对多次波的模拟，该技术能适应任意观测系统，并且不受炮检点位置的约束。具体过程如下：首先对单炮数据进行时间反转，然后再向下外推，并与海底的反射系数进行褶积，再做向上的外推处理，最后完成整个单炮的多次波建模[6-8]。

2.2 曲波域多次波模型优化

广义自由表面多次波预测产生多次波模型，然后将地震数据和模型数据转换到曲波域，对多次波模型进一步优化，最后利用原始数据与多次波模型相减，对多次波进行压制。曲波变换使用的是第二代曲波变换，解决了第一代曲波变换大量数据冗余的问题，使曲波变换的实现更简单，运算效率更高。第二代曲波变换的公式为

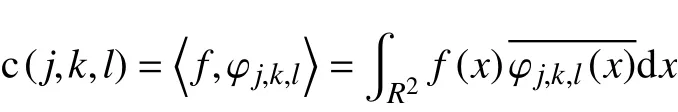
其中，f（x）表示输入的原始地震信号或者多次波模型数据；φj,k,l为曲波函数，c（j,k,l）为曲波系数，其中j为尺度，l为方向，k为尺度j在l方向上的矩阵系数[10-13]。

具体的模型优化流程见图1，将地震数据和广义自由表面多次波预测产生的模型数据分为两部分，一部分是低频数据，一部分是高频数据，其中低频数据利用常规自适应减的方法得到低频多次波模型；高频数据动校后转换到曲波域，在曲波域中，比较不同尺度、不同角度的信号与多次波的振幅和相位差异（图2），具体的做法是：当信号与多次波的模型比较大于门槛值时，认为是信号，小于门槛值时，认为是多次波，依次来优化高频多次波模型，从而得到更加精确的多次波模型，再进行反动校（图3），最后用地震数据减去多次波模型，达到压制多次波的目的[14-17]。分高低频的主要原因是，在曲波域中，低频部分无法分角度和尺度对数据进行比较，见图4（分三个尺度）中Scale1，对低频模型无法进行优化，因此低频数据采用常规的自适应减，在高频数据中采用曲波变换对模型进行优化。高低频分界点的选取要稍大于Scale1的频率，低于Scale2的频率。

3 实例分析

选取印度洋某深水海域的地震资料，该地区海底地形总体较为平坦，最大水深为5258 m。从原始炮集（图5）上可以看出，多次波主要是海底相关的多次波，图6是有效波与多次波频谱图的对比，其中红色是有效波频谱图，蓝色是多次波的频谱图，从图中可以看出，多次波能量强，频带宽，与有效波频谱基本一致。首先利用常规的广义自由表面多次波压制方法对其压制，图7是利用广义自由表面多次波压制方法得到的多次波模型，图8是压制后的炮集，可以看出多次波压制不干净，仍有较多残留。图9是利用本文方法，分4个尺度进行曲波变换，计算Scale1的频率为15.75 Hz，因此本文将原始数据和模型数据以20 Hz为界分为高频数据和低频数据，低频数据利用常规的自适应减的方法优化低频多次波模型，高频数据转到曲波域，在曲波域中根据不同尺度不同角度的信号与多次波的振幅和相位差异来优化高频多次波模型，然后将低频模型和高频模型相加得到优化后的多次波模型。为了更清晰地比较优化前后的多次波模型，将原始炮集的多次波与优化前后的多次波模型放大并进行比较，图10可以明显地看出，由浅至深，优化后的多次波模型与原始炮集的多次波更吻合，多次波模型的精确度更高。最后利用原始数据直接减去多次波模型，得到压制后的炮集，可以看出压制后炮集更干净，信噪比更高（图11）[18-21]。

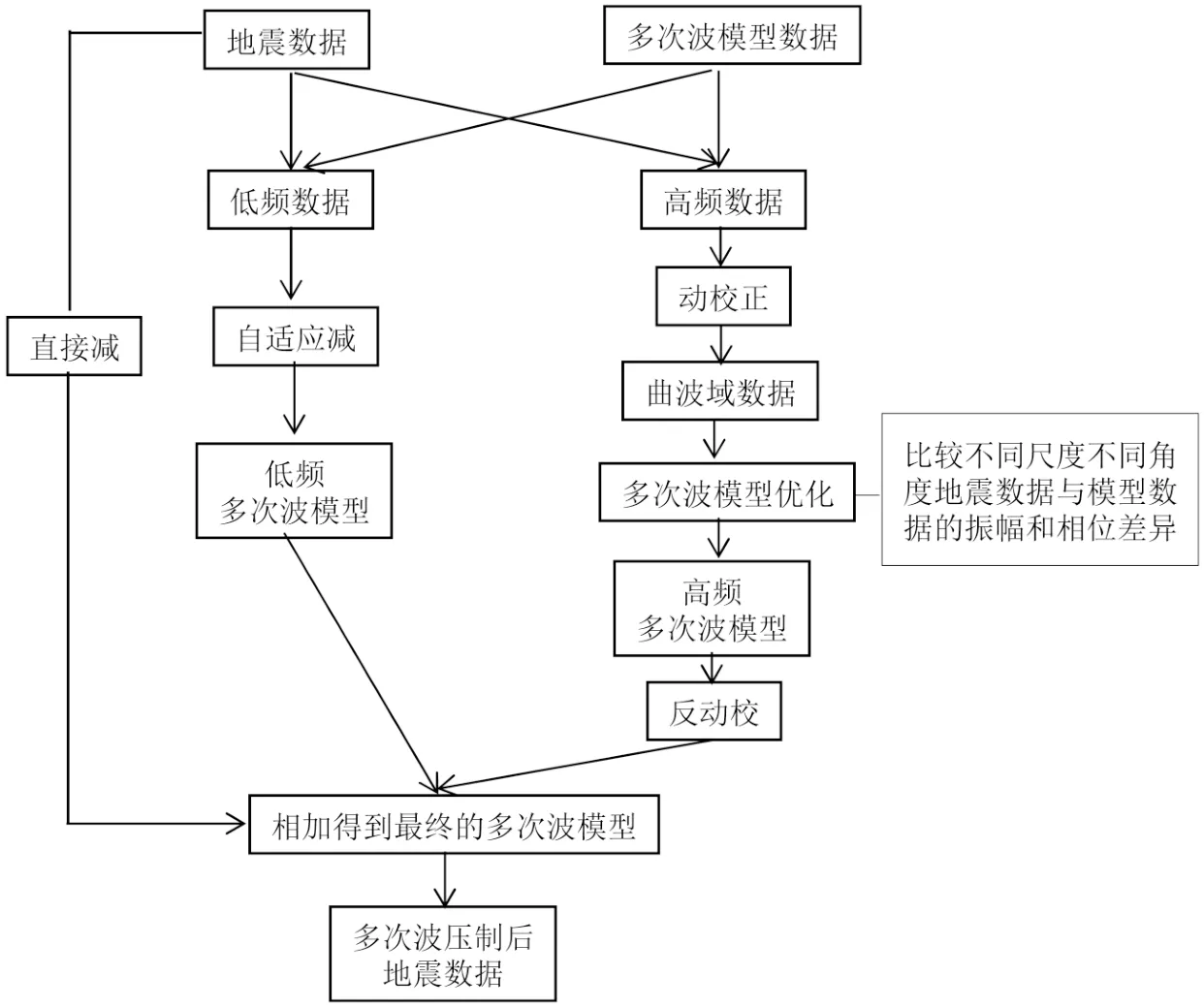
图 1 模型优化及多次波压制流程Fig.1 Model optimization and multiple suppression process

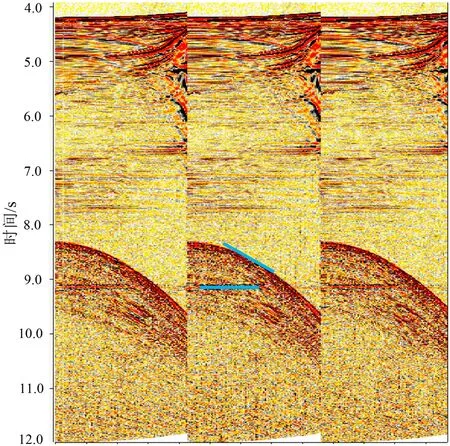
图 2 多次波与有效波角度的差异Fig.2 Angle difference between multiple and effective waves

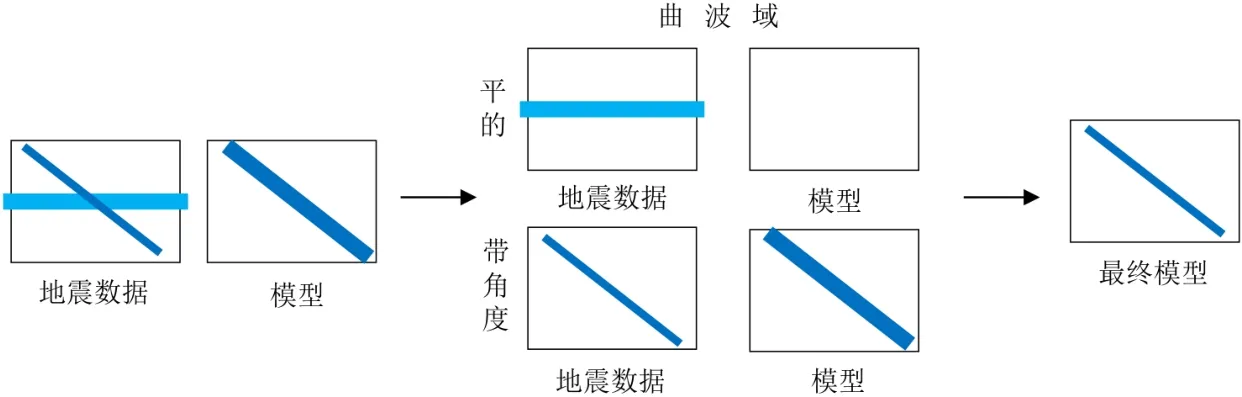
图 3 曲波域多次波模型优化思路Fig.3 Optimization of multiple-wave model in curvelet domain

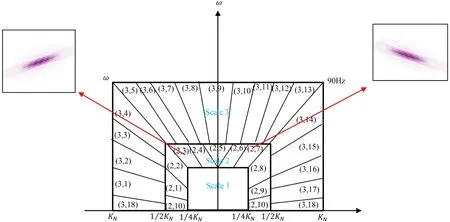
图 4 曲波变换示意图ω为频率，KN为空间奈奎斯特频率，N为尺度。Fig.4 Schematic diagram of curvelet transformωis the frequency, KNis the space Nyquist frequency, Nis the scale.

图 5 原始炮集Fig.5 Original gun set

图 6 有效波与多次波频谱图对比红色是有效波频谱，蓝色是多次波频谱。Fig.6 The spectrum of the effective wave compared with that of the multiple wave where red is the spectrum of the effective wave and blue is the spectrum of the multiple wave.

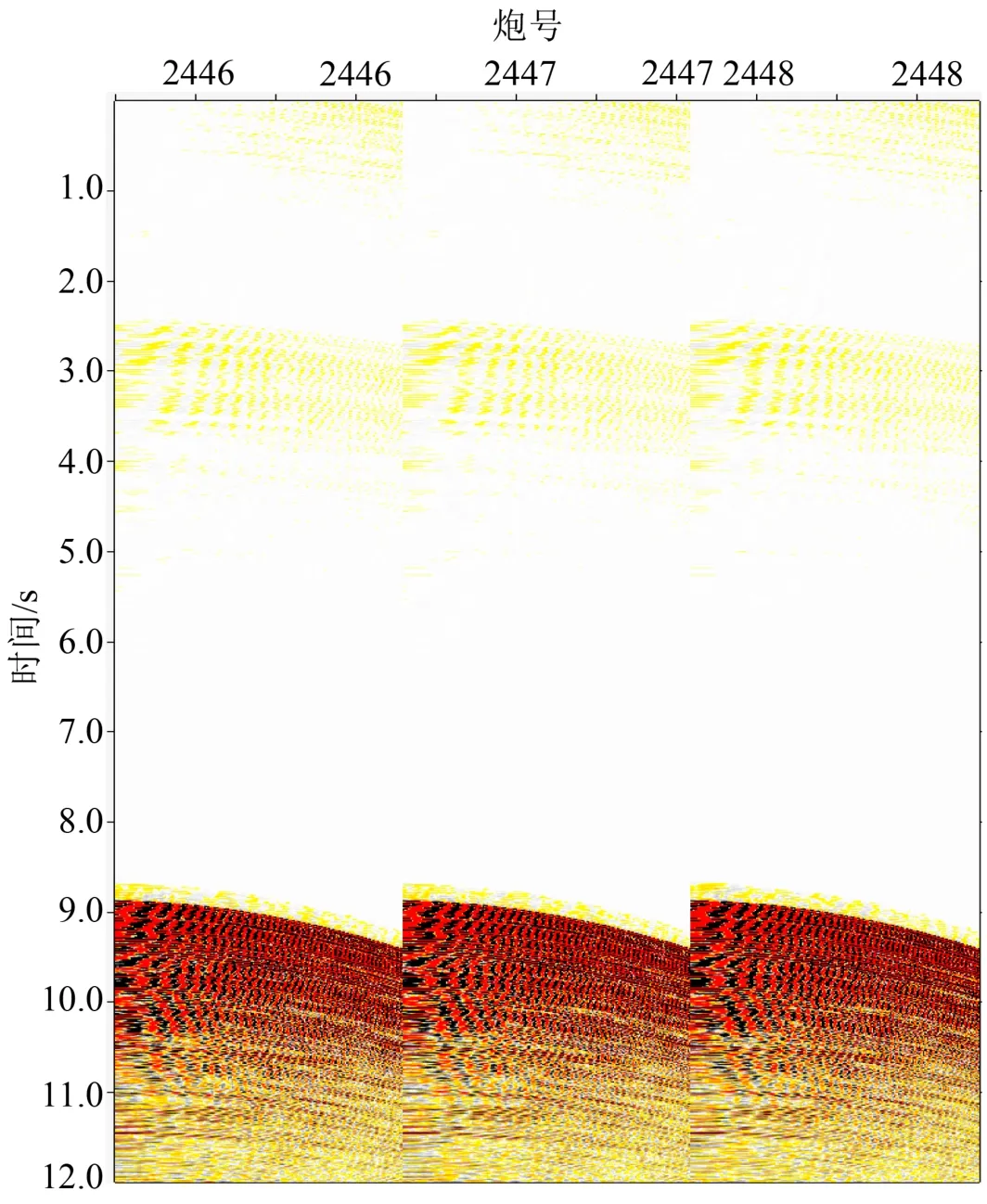
图 7 常规方法得到的多次波模型Fig.7 Multi-wave model obtained by conventional method

图 8 常规方法压制后的炮集Fig.8 A shot set after suppression by conventional method

图 9 曲波域优化后多次波模型Fig.9 Optimized multiple wave model in curved wave domain

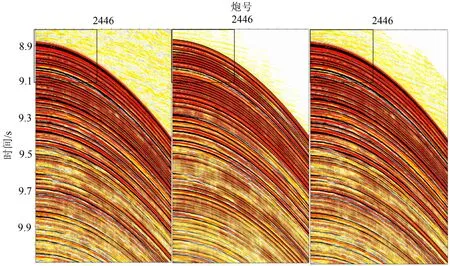
图 10 多次波模型对比图从左到右依次为：原始数据多次波，常规方法得到的多次波模型，曲波域优化后的多次波模型。Fig.10 Multiples model comparison chartFrom left to right: multiples of raw data, multiples model obtained by conventional method, multiples model obtained by curvelet transform.

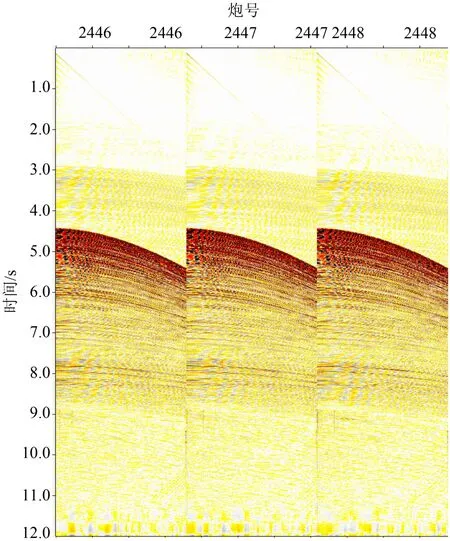
图 11 利用优化后模型多次波压制效果Fig.11 Suppression of multiple waves using the optimized model

下面从叠加剖面上看常规方法和本文方法的压制效果。选取印度洋该深水海域两条测线，图12是A测线原始剖面，图13是利用常规方法压制后的效果，可以看出压制效果不理想，多次波残留较为严重（图中箭头所指的地方）；图14 是利用本文方法压制后的效果，可以看出，压制效果较好，多次波去除的较为干净，剖面信噪比高，并且未损害有效信号，时间10.2 s的位置波组特征更加清晰，有利于后期地震资料的偏移和解释[22-25]。图15—17是B测线的原始剖面及利用常规方法和本文方法压制后的效果图，同样可以看出，利用本文方法压制多次波的效果更好，压制后的剖面信噪比更高，说明本文方法更适用于深水海域海底相关多次波的 压制。

图 12 A测线原始叠加剖面Fig.12 The original profile of line A

图 13 A测线常规方法压制后的叠加剖面Fig.13 The superimposed profile after conventional method of line A

图 14 A测线利用曲波域优化模型压制的叠加剖面Fig.14 The stacked profile after optimization model in curved wave domain of line A

图 15 B测线原始叠加剖面Fig.15 The original profile of line B

图 16 B测线常规方法压制后的叠加剖面Fig.16 The superimposed profile after conventional method of line B

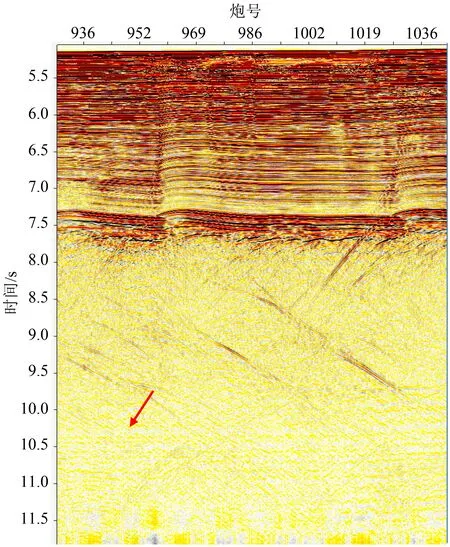
图 17 B测线利用曲波域优化模型压制后的叠加剖面Fig.17 The stacked profile after optimization model in curved wave domain of line B

4 结论

本文通过在实际资料中的应用可以看出，多次波的压制效果较好，剖面的信噪比得到了较大的提高，同时压制后有效信号得到了凸显，波组特征更加清晰，有利于后期层位的识别和追踪。

该技术适用于海底地形较为平坦的深水海域，同时值得注意的是，本文方法在曲波域中对高频模型进行优化时，是根据信号和模型数据在不同尺度、不同角度上的振幅和相位差异，即当信号与多次波的模型比大于门槛值时，认为是信号，小于门槛值时，认为是多次波，因此门槛值的选择非常重要，直接决定优化后模型的精确度。门槛值的选择是选取有代表性的炮集，计算不同尺度、不同角度的振幅和相位差异，从而确定门槛值。