稳杠杆和稳增长目标下最优货币政策规则

赵米芸

(长安大学 经济与管理学院，陕西 西安 710064)

借贷对经济活动至关重要，但是杠杆与风险有着千丝万缕的联系。诸如20世纪80年代拉美债务危机、1997年东南亚金融危机、2008年美国次贷危机以及2009年欧洲主权债务危机等系统性风险的爆发皆与杠杆攀升相伴而生。杠杆率波动影响货币政策传导机制与金融经济稳定已经成为新的共识[1-2]。过度负债不但为危机的发生奠定了基础，而且持续阻碍着经济复苏。也就是说，高杠杆在影响危机长度与深度的同时还影响着经济复苏过程与程度。中国为应对全球金融危机，2013年“三期叠加”重要战略判断、2015年供给侧结构性改革、2016年金融去杠杆、2017年三大攻坚战以及2019年金融供给侧结构性改革等各种调控措施紧密出台。很显然，宏观政策调控的重心逐渐转向了稳杠杆(防风险)。当前中国货币政策更加注重风险防范和经济稳定，“稳杠杆”和“稳增长”成为了中国货币政策调控的重点和现实目标[3]。

各国中央银行防范化解金融风险、确保经济稳定的方式迥异。美联储选择“善意忽视”，仅在资产价格泡沫破灭后“收拾残局”(1)Mishkin F S.Monetary policy strategy:lessons from the crisis.NBER Working Papers,2011,No.16755.；欧洲央行奉行“双支柱策略”，考虑经济因素的同时赋予信贷走势等货币因素更高权重；日本央行按照“缺口学”，重点盯住产出缺口，严格限制信贷债务规模。可见，政策调控实践中将金融变量引入中央银行政策目标体系已经在一定范围内成为共识。

弹性通胀目标制作为全球金融危机前的最优货币政策框架，危机后毋须全盘否定[4]。在弹性通胀目标制下，中央银行应尽可能地通过信贷债务、资产价格等金融变量波动来形成产出缺口和通胀率，避免忽视物价稳定下金融过度繁荣所累积的潜在风险。这说明描述中央银行货币政策反应函数可能包含损失函数中不存在的变量。同时，Bordo et al.主张央行“逆风操作”[5]，这是因为过度债务可能积累产出通胀的未来问题，温和的经济环境往往易于滋生“非理性繁荣”，从而加速信贷繁荣和过度负债下经济高杠杆化[6]。2009年欧洲主权债务危机后，欧洲央行于2011年已经开始监测其成员国宏观杠杆率与其长期趋势偏离值。货币政策若忽略宏观杠杆率这一金融因素，甚至拒绝该因素进入货币当局的政策制定和调整过程，则可能使货币政策反映的相关信息出现失真，货币政策的实践效果也会大打折扣。因此，稳杠杆和稳增长目标下中国央行货币政策是否应当以及如何对宏观杠杆率予以反应值得进一步展开研究。

一、文献综述

著名的“规则对相机抉择”之争中，“规则行事”强调央行制定货币政策时应该遵循事先确定的量化规则，“相机抉择”则强调根据实时经济状态不断重新优化决策[7]。货币政策的“相机抉择”存在动态非一致性，会产生通胀性偏差和稳定性偏差，使社会福利产生损失，政策规则称为“最优规则”和“预先承诺”的解决方案，从而产生动态优化问题。相应地，“相机抉择”政策被称之为“不一致”“欺骗”和“目光短浅”的解决方案。根据政策工具分类，货币政策规则包括数量规则和利率规则。最优货币政策规则，是指在既定的决策约束(技术约束、资源约束及信贷约束)下，中央银行为实现最小化经济波动或者最大化社会福利而具体实施的明确规定货币政策干预对象和干预能力的货币政策调控规则。按照最优货币政策规则的演化发展脉络，其求解方式主要归纳为两种：一是总需求和总供给(IS-Phillips)模型框架下，以最小化由产出缺口和通胀波动二者加权之和所刻画的中央银行二次损失函数为目标，利用动态最优控制技术获得最优货币政策规则[8]；二是NK-DSGE模型框架下，以最大化社会福利为目标，从一般均衡理论出发通过动态最优化方法刻画经济主体的跨期优化问题，选择最优货币政策规则。幸运的是，在二阶近似范围内最小化中央银行损失函数等同于最大化社会福利目标函数，即中央银行二次损失函数和社会福利目标函数的最终目标相一致[9]。

需要注意的是，评价不同货币政策规则，首要问题是货币政策的目标应该是什么？货币政策的重点在于价格稳定，但是仅以通胀和产出为政策目标的宏观政策已难以适应金融稳定要求[10]。除了通胀和产出，央行损失函数还应该纳入金融稳定指标。宏观杠杆率作为金融风险的有效先行指标，Hallett et al.将其(债务与GDP的比值)纳入泰勒规则，使用实时数据估计欧洲央行泰勒规则表明利率对债务水平有显著反应，货币政策在预期债务与GDP比率每上升2.5个百分点时将会收缩25个基点[11]。Angeloni et al.采用嵌入银行中介的标准新凯恩斯主义DSGE模型研究银行挤兑风险后发现，货币政策不仅可以应对产出波动和通胀，还能应对杠杆作用[12]。货币政策通过风险承担渠道和利率渠道作用于银行信贷杠杆[13]，低利率政策抬升银行杠杆的同时会增加银行风险[14]。此外，陈创练等研究表明，数量型和价格型货币政策盯住杠杆周期的政策偏好皆具适时调整性，前者调控杠杆率时更为有效[15]。藉此本文在包含异质性代理人和金融摩擦的NK模型框架内，通过自然利率内生决定方程间接地将宏观杠杆率引入动态IS曲线，同时采用Calvo价格设定方式下的后顾型Phillips曲线，赋予总需求和总供给微观基础。在中央银行二次损失函数、动态IS-NK-Phillips曲线、宏观杠杆缺口作用下的自然利率内生决定方程构成的宏观经济约束环境下，求解中国双目标下不同规则的最优反应函数和政策效果，寻找当前中国最优利率规则、数量规则稳杠杆、稳增长的政策优势。

二、双重目标下最优货币政策规制理论推演

理论上，在IS-Phillips模型框架下运用央行二次损失函数获得最优货币政策规则已成为最优货币政策研究中的主要手段[8]。本文对Svensson理论框架作出改进，参照Benigno et al.关于债务水平引入自然利率内生决定方程的做法(2)Benigno P,Eggertsson G B,Romei F.Dynamic debt deleveraging and optimal monetary Policy.CEPR Discussion Paper,2016.，通过将宏观杠杆率引入自然利率内生决定方程后得到与标准新凯恩斯模型形式相类似的动态IS曲线，以刻画货币政策反映宏观杠杆率波动的事前干预观与事后反应观的整体框架。

(一)宏观杠杆率与动态IS曲线

遵循Benigno et al. 研究思路①，假定经济体中存在无限期存活经济行为人，包括χ占比储蓄者(saver)和1-χ占比借款者(borrower)，分别用上标s和b表征。代表性经济行为人的效用函数、预算约束和借贷利率分别为

(1)

(2)

(3)

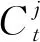
为简化处理过程，本文设定βs→βb=β。在预算约束和最优借贷上限约束下家庭效用函数最大化，储蓄者和借款者的欧拉方程分别为

(4)

(5)

(6)

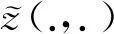
(7)

(8)

当产品市场均衡时，储蓄者和借款者的消费总额与经济体的实际产出相等。稳态附近线性化得出动态线性方程，整理后得到与标准新凯恩斯模型形式相类似的动态IS曲线

yt=Etyt+1-σ(it-Et(πt+1-π*)-rt)

(9)

rt=-χ(λ+φ)(bt-dt)

(10)

式中：yt、πt和rt分别表示t时期的产出缺口、通胀率和自然利率，σ为贴现因子，π*为目标通胀率，λ≡zb(1)>0，φ≡φb(1)>0，且zb(·)、φb(·)分别是函数z(·)和φ(·)关于bt的一阶导函数。不同于标准新凯恩斯模型中自然利率rt是外生给定的，该模型中rt是内生决定的。这表明即使总需求仍然取决于预期收入和实际利率，但私人债务水平也会影响标准总需求关系。特别是如果私人实际债务水平bt高于目标债务水平dt时，过高私人债务将触发对自然利率的负向冲击，从而对总需求产生负向冲击；同样如果私人实际债务水平bt低于目标值dt时，债务人仍有举债空间，等同于正向总需求冲击。

进一步，选取宏观杠杆率leveraget和可持续宏观杠杆率leverage*分别表征实际债务水平bt、目标债务水平dt，则式(10)可表述为

rt=-ω(leveraget-leverage*)

(11)

式中：ω=χ(λ+φ),ω>0。

(二)最优利率和数量规则推演

结合央行二次损失函数和宏观经济环境约束方程，央行货币政策行为决策描述为下述系统方程组

(12)

πt+1=πt+αyt+εt+1

(13)

yt+1=β1yt-β2(it-Et(πt+1)-rt)+ηt+1

(14)

rt=-ω(leveraget-leverage*)+υt

(15)

式中：L(.,.)代表央行损失函数，δ表示贴现因子，κ衡量实际产出和通货膨胀损失的相对权重，其他变量含义与上述相同。系数α、β1、β2均大于0，且β1<1，因而当实际产出受到冲击时，产出缺口将会收敛于0。εt+1、ηt+1和υt分别代表通胀率、总需求以及自然利率的外生冲击，三者均服从均值为0、方差为常数的正态分布。

本文所构建的理论模型有两点创新：式(14)、(15)通过自然利率内生决定方程间接地将宏观杠杆缺口加入动态IS曲线，力图把货币政策如何反映宏观杠杆率波动的事前干预观与事后反应观融合在一个框架中。央行损失函数式(12)未包含宏观杠杆率，但约束条件式(13)～(15)引进了宏观杠杆率，推导出的货币政策规则包含了宏观杠杆率，因而体现了直接反应观；此外，式(12)～(15)构成的系统模型能够评估宏观杠杆率波动对产出缺口、通胀率的影响，因此体现了间接反应观。需要强调的是，式(14)是结合中国投资率偏高呈现上升态势、消费率偏低呈现下降态势，以及经济增长波动主要由投资引起的经济事实修正而得到的后顾型总需求方程，这一做法与郑挺国等研究保持一致[16]。

采用动态规划方法并利用值函数求解上述无限期动态最优化问题，理论推演得出最优利率规则；进一步结合货币需求方程所刻画的名义利率it、货币增长率mt和产出缺口yt间的关系

it=r1yt-r2mt+νt

由于执法团队建设质量会对保障体系落实与农产品质量监管效果形成直接影响，所以各基层组织应做好执法团队建设工作，打造出一支综合素质过硬的保障体系执法团队。

(16)

式中：r1、r2为参数，νt为名义利率外生冲击。

得最优数量规则

(17)

(18)

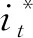
顾及资本市场扰动、政策反复信誉鸿沟和各方面支持政策调整，央行货币政策实践中通常不会对政策利率和货币供应量进行“突变式”的矫正，而是基于上期政策利率和货币供应量渐进式调整至目标水平，即政策利率和货币供给往往具有惯性、存在平滑行为[17-20]。遵循上述做法，引入央行货币政策调整动态平滑机制后得最终估计方程

(19)

(20)

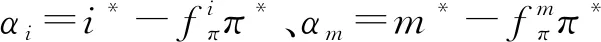
三、双重目标下最优货币政策规则特征检验

(一)数据选取与统计描述

本文选取1996年第一季度至2020年第四季度共100个季度时间序列数据对上述理论推演得来的最优利率规则和最优数量规则实证检验。变量包括宏观杠杆缺口(levgapt)、产出缺口(yt)、通胀率(πt)、名义利率(it)、货币供应量增长率(mt)。数据来自Wind资讯和中国人民银行网站。

宏观杠杆缺口由中国宏观杠杆率HP滤波退势后得到。实际产出由名义GDP除以平减指数得到，即实际产出=名义GDP/同期CPI，并对实际产出季节调整后HP滤波处理得到潜在产出，计算产出缺口=100 (实际产出-潜在产出)/潜在产出。此处，平减指数由消费者价格指数CPI环比数据经过统一量纲处理后计算得到定基物价指数(1996年取值100)。考虑到消费者价格指数CPI能较为全面地反映物价总水平变动，且与国内生产总值GDP关系紧密，故选取CPI来衡量通胀率。选取7天银行间同业拆借利率作为市场利率的代理变量，广义货币供应量M2增长率作为货币供应量增长率的代理变量。相关变量的统计描述如表1所示。

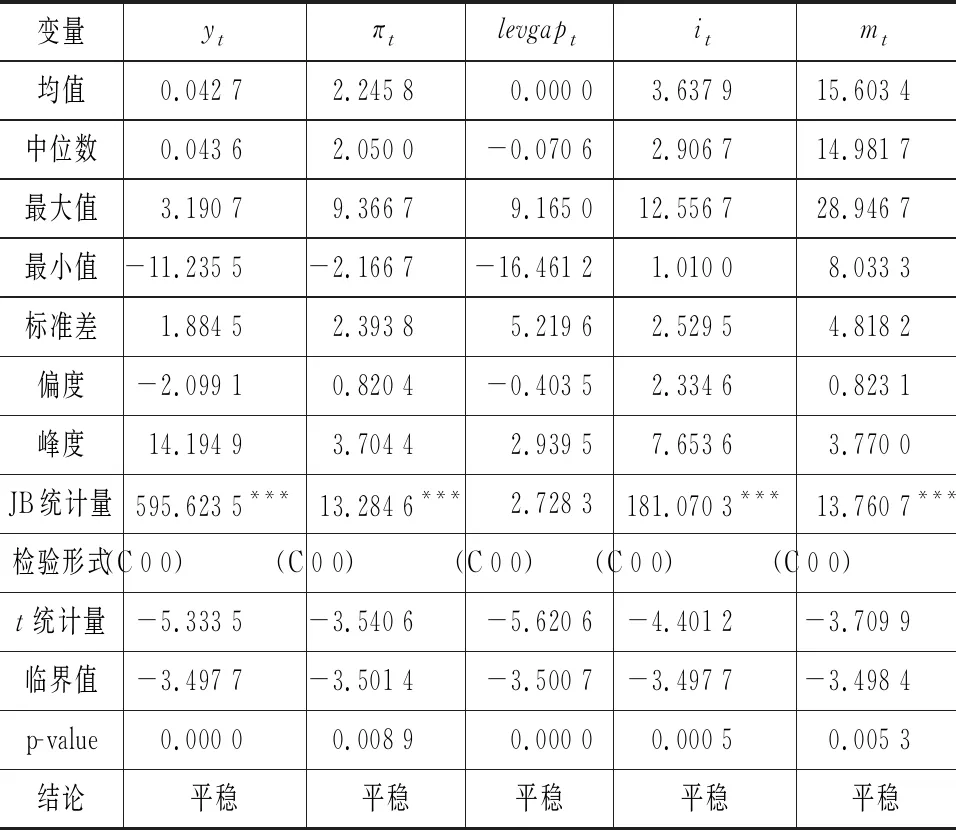
表1 样本各个时间序列数据的统计描述

(二)固定参数的最优货币政策规则估计结果

表2 GMM方法估计结果

(三)时变参数的最优货币政策规则估计结果

现实经济受外部冲击和内部扰动影响总处在不断变化之中，央行货币政策对物价水平、实体经济和宏观杠杆可能持有阶段性立场，货币政策反应系数可能在样本期间发生转变。为捕捉经济环境和政策规则的动态演变，采用状态空间模型(state space model)研究中国货币政策设定结构的时变特征。状态空间模型量测方程为

(21)

(22)

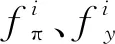
由图1(a)可知，利率政策盯住通胀目标的时变系数在绝大部分样本期都小于1，表明利率政策对通货膨胀反应有待进一步加强。具体地，名义利率在2006年前关注通胀力度较大，2007年至2008年进入调整期，盯住通胀系数在2008年第三季度达到最低位。2009年第二季度后盯住通胀力度逐渐加大，尤其是2015年经济步入新常态后盯住通胀系数明显上升，2017年至2020年呈平稳走势，一直处于0.67左右。M2增长率盯住通胀目标系数的动态变化如图1(b)所示，2000年盯住通胀目标的系数为正，货币供给出现短暂顺周期调节状态，这可能是亚洲金融危机后为稳经济、促增长实施的正向刺激，在一定程度上容忍通胀压力。此后时变系数基本均为负，货币供给政策开始逆周期调控通货膨胀，2001年至2004年第一季度时变系数绝对值均小于1，货币供给政策较弱关注通胀；2004年第二季度开始时变系数绝对值均大于1，调控通胀力度逐步增强，但2008年第二季度盯住通胀系数达到2004年以来最低位，央行减弱关注通胀；短暂调整后，盯住通胀系数绝对值从2010年第四季度的2.58逐渐上升至2020年第四季度的5.09。从时变系数均值看，通胀率每提高1个百分点，名义利率平均上调0.719个百分点，M2增长率下降2.438个百分点。可见，最优数量规则稳价格力度更强，央行关注稳增长同时容忍温和通胀偏好较强。

最优利率规则中，盯住产出缺口的系数动态演变呈现两轮先降后升态势，见图1(c)：第一轮是从2000年第一季度的1.28下降至2003年第四季度的0.23后逐步回升，这一时期国内处于后危机时期的通缩阶段，利率政策较弱盯住产出缺口。第二轮是从2006年第一季度的0.73下降至2007年第一季度的0.15后迅速回升至2009年第一季度的1.27。此后盯住产出缺口系数进入持续下降通道，2020年处在0.66左右，名义利率调控实体经济力度明显减弱。在最优数量规则中，盯住产出缺口的时变系数，见图1(d)，2000年至2008年呈正负切换逐渐收敛于零。2009年开始，盯住产出缺口的系数均为负，受全球金融危机影响中国经济增速放缓，央行开始刺激经济增长，且在2009年达到极大值，此后调控力度逐渐下降至2020年第四季度的-5.62。可见，时变系数路径很好地刻画了2008年全球金融危机爆发前后中国经济增速放缓、“四万亿”刺激政策实施以及经济转向高质量发展等阶段性重大调整。从时变系数均值看，产出缺口每提高1.000个百分点，名义利率平均上调0.813个百分点，M2增长率下降4.693个百分点，可见，最优数量规则稳增长强度较大。

名义利率盯住宏观杠杆缺口的时变系数分层明显，见图1(e)：2008年第四季度以前均小于零，表明顺周期下调利率，加剧杠杆高企；2008年第四季度以后均大于零，表明逆周期上调利率，抑制杠杆攀升。从数值大小看，2008年金融危机使经济增速放缓同时导致高杠杆问题凸显，时变系数转负为正、数值持续增大，从2008第四季度的0.03逐渐增加至2013年第二季度的0.16后小幅波动，2017年后稳定维持在0.17左右直至2020年新冠肺炎疫情冲击出现小幅下降。M2增长率盯住宏观杠杆缺口的时变系数，见图1(f)，2005年第二季度前皆为正，表明宏观杠杆率增加时，央行会增加货币供给，使宏观杠杆率进一步攀升。此后时变系数基本均为负，反映出宏观杠杆率增加时，央行下调货币供给，稳杠杆目标明确。从数值大小看，2005年第三季度至2009年第四季度时变系数波动剧烈且绝对值均小于1，说明货币供给政策稳杠杆意图较弱；2010年以来调控力度逐渐增强，时变系数稳定在-1.3左右，尤其是2016年开始反应力度攀升，时变系数基本维持在-1.75左右，但2020年呈减弱态势。这是由于全球金融危机后，高杠杆和经济下行蕴含较大的金融风险，为防范化解重大风险，央行增强对宏观杠杆逆周期反应力度，稳杠杆意图非常明显，但面对诸如全球金融危机和新冠肺炎疫情等重大经济冲击时更加注重稳增长，包容宏观杠杆率适度抬升，偏好适宜杠杆率水平。从时变系数均值看，宏观杠杆缺口每上升1.000个百分点，名义利率平均调高0.013个百分点，M2增长率下降0.542个百分点，可知最优数量规则对宏观杠杆率反应更为剧烈。

图1 状态空间方法估计的时变参数序列趋势

上述时变参数序列表明央行货币政策调节通货膨胀、实体经济和宏观杠杆的反应力度动态演变，既与理论更加贴近，又与中国货币政策实践以及宏观经济运行状况相一致，在一定程度上体现出货币政策对各经济变量的重视程度以及稳杠杆和稳增长的本质意图。首先，名义利率和M2增长率在2010年后盯住实体经济力度有所减弱，盯住通胀和杠杆力度逐渐增强。其次，2008年全球金融危机前后，时变参数分层非常明显，而后经济迈入新常态，政策取向趋于稳健。最后，面对诸如2008年全球金融危机和2020年新冠肺炎疫情等重大经济冲击时，央行通常更加偏好实际产出，包容宏观杠杆率适度抬升和温和通胀。

四、结语

经济增速放缓和杠杆攀升并存，为防控金融风险，稳杠杆和稳增长成为当前中国货币政策调控的现实目标。货币政策如何对宏观杠杆率作出反应成为亟待解决的问题。本文理论推演了包含宏观杠杆率的最优利率与数量规则，并利用GMM和State-Space方法分别估计了中国货币政策对通胀目标、实体经济、宏观杠杆的固定和时变反应关系，从而回答货币政策是否盯住宏观杠杆率以及如何盯住宏观杠杆率，以及央行稳杠杆和稳增长的本质意图是否出现了转变的问题。

实证结果表明，中国最优利率政策操作相比最优数量政策更具主动性。最优利率规则盯住通胀目标的反应参数大多数小于1，是一种内在不稳定的规则，需要进一步拓宽优化中国利率政策框架，延伸名义利率调控通货膨胀、实体经济和宏观杠杆的宽度，由不稳定规则转变为稳定规则。尽管如此，仍然能够从最优利率规则和数量规则中把握央行货币政策调控的本质意图。具体地，最优利率规则和数量规则均具有显著盯住宏观杠杆的政策取向，稳杠杆意图显著。名义利率对产出缺口反应较为充分，M2增长率对实际产出反应较为强烈。最优利率规则促增长同时宏观杠杆率较为稳定，而最优数量规则熨平经济波动同时容易引发宏观杠杆率大幅波动。2008年全球金融危机前后，中国货币政策对实际产出、通货膨胀和宏观杠杆的调节转变较大，时变系数分层明显。随着中国经济持续高质量发展，货币政策取向趋于稳健，但是面对重大经济冲击时央行更加注重稳增长的同时包容温和通胀和适度杠杆。可见，央行应对宏观杠杆率予以关注，发挥利率政策促增长的同时把好货币供应总闸门才是有效遏制宏观杠杆快速攀升、助力稳杠杆和稳增长动态平衡的根本策略。同时，央行也需要进一步增强利率政策对宏观杠杆目标的调节功效，从而促进宏观经济可持续高质量发展。