点云库在兼容系统中的编译及邻域搜索

董路通 朱留存 张恒艳

（扬州大学信息工程学院 江苏省扬州市 225127）

三维激光扫描技术源自于上世纪九十年代，它采用高速激光扫描测量方式，大面积高分辨率地快速获取被测对象表面的三维坐标数据（点云数据），可以快速、大量的采集空间点位信息，较传统单点测量方法，它速度更快精度更高抗干扰性更强。随着社会的发展，利用三维激光扫描仪快速高效获取目标物体的点云数据集越来越庞大，但所采集的数据集中通常无明显的几何拓扑信息。由于数据集的庞大，所以提前建立点云拓扑关系，高效的有组织的管理点云，是对海量点云数据处理的前提。

在处理众多点云数据时，我们需要对某一点进行邻域查找，我们首先应该对原始的散乱的点云建立一定的拓扑关系，准确的建立邻域拓扑关系后不仅在目标点的搜索查找范围会缩小，而且更为后期的有效压缩配准提供了保障。基于K-D 树的近邻搜索是二进制空间分割树的特殊的情况，且具有有很高的搜索效率，K-D 树可以使用在多种应用场合，如多维键值搜索、K 近邻搜索，该数据结构建树速度快，可以很快地知道目标物体在3D 场景中的位置，或侦测目标节点是否在可视范围内。本文结合PCL 开源库，针对海量点云数据建立K-D 树数据结构，实现点云的快速邻域搜索。

1 PCL

PCL 是在吸收前辈点云相关研究的基础上建立起来的大范围、独立的、跨平台的开源C++编程库，主要用于二维或三维的图像和点云处理，可以在Windows、Linux、Android 和部分嵌入式实时系统上运行。PCL 起初主要应用于机器人研究，后来与全球3D 信息获取、处理的研究者们一起，组建了强大的开发维护团队，发展异常迅速。如同OpenCV 在2D 信息处理的地位一样，PCL 主要运用在3D 信息的获取与处理[1]。

为了简化开发，PCL 被分成一系列较小的代码库，这些代码库可以单独编译。这种模块化对于在计算或者大小限制较少的平台上发布PCL 非常重要。如图1所示。

图1：PCL 功能模块

2 Windows系统

在PCL 官网中列出的在Windows 下安装PCL 教程分为两步：安装PCL 依赖库和编译PCL 文件，介于操作的复杂性，也同时便于初学者安装，暂不采用此方法安装。本文介绍的编译环境是Visual Studio 2019，操作系统为64 位 Windows 10。

2.1 PCL安装包的下载

在Github 中下载PCL 最新版本的PCL-1.12.0-AllInOnemsvc2019-win64.exe 和pcl-1.12.0-rc1-pdb-msvc2019-win64.zip， 下载完成后安装.exe 文件。pdb 文件是程序的数据库文件，是VS 编译的生成文件，要想正常运行PCL 文件必须要有pdb 文件。将pdb文件解压后的文件移动到PCL 安装目录中的bin 文件中，如图2所示。

图2：配置PCL 文件

2.2 配置环境变量

右键此电脑，找到高级系统设置中的环境变量。如图3所示。

图3：环境变量

首先配置在环境变量中系统变量的Path 变量，将以下路径添加到Path 变量中后确定。如图4所示。

图4：Path 变量

2.3 包含目录配置和库目录

在VS2019 中新建空项目，在其配置属性界面中找到包含目录，将第三方包含目录和库目录分别添加到相应目录中。包含目录的意思就是在编译的过程中引用的头文件一定要被工程所包含，否则的话是无法确定头文件的位置，所以我们需要在目标地址中包含我们安装好的库的头文件。库目录就是动态链接库所存在路径，如图5、图6所示。

图5：包含目录

图6：库目录

2.4 输入附加依赖项

在“配置属性-链接器-输入”中编辑路径，将本文安装的几个第三方依赖库静态链接库名称全部添加进去，此库目录可以在相应的安装目录下找到[1]。部分静态链接库如图7所示。

图7：部分静态链接库

2.5 运行测试代码

此时在VS2019 中新建C++文件，在Github 官网中获取一段代码添加到VS 中即可运行。

3 Linux系统

本文的Linux 安装平台为Ubuntu 20.0，运行在虚拟机中，和Windows 系统一样，我们首先去Github 官网中下载PCL 安装包，根据PCL 官网安装教程，我们下载的PCL 安装包版本为pcl-1.11.0，格式为tar.gz。首先打开下载的安装包界面的终端界面，输入命令，将其解压。如图8所示。

图8：解压命令

3.1 安装依赖库

在Ubuntu 中安装PCL 时需要大量依赖库，为了保证能正常安装PCL，我们首先下载所需要的各种依赖库。在Ubuntu 系统中输入图9 命令并顺利完成后，即可继续完成后续操作。如图9所示。

图9：PCL 外部依赖库

3.2 运行cmake ..

在解压后的文件夹中新建build 文件夹，可以通过执行mkdir build 命令来完成操作。根据官网提示，接下来运行cmake 命令，cmake 是make system 的一个指令，编译他的上一级到我们当前的目录里面，然后在新建完成的build 终端下执行 cmake..命令，运行完成后如图10所示。

图10：运行完成的cmake

3.3 运行 make-j4

在虚拟中运行速度比较慢，所以在编译的过程中需要点时间，图11 是运行此命令常见的错误，此错误的解决办法只需要将虚拟机的内存配置更大一下，就完美解决，命令运行完毕如图12。

图11：运行过程中出现的错误

图12：运行完成

3.4 安装PCL库

在build 终端中输入命令 make-j4 install，如果没有改变PCL安装位置的变量的话可能没有权限，则需要运行sudo make-j4 install 命令，使用管理员身份进行安装。安装完成后，我们所需要的PCL 在Linux 系统中的平台已经搭建完成。

相较于在Windows 中，在Ubuntu 下的搭建操作更为简单，用户如果在初级学习PCL 阶段可以安装虚拟机Linux 系统，但由于虚拟机中的显卡是虚拟出来的，所以运行一写代码速度相对比较慢，内存占用比较多。如果是在高级学习阶段或者相关职业从事者建议使用双系统或者双机独立系统。

4 近邻搜索

在点云配准或其它点云处理过程中，有时需要以点云中的某个点为中心，寻找它的邻域，所以我们需要对原始的散乱无序的点云建立一定的拓扑关系，方便我们对其邻域的搜索。现阶段常用的建立点云拓扑关系的方法有许多，如Octree 法、K-D 树法和三维栅格法，其中基于K-D 树的方法由于其高效的搜索性能和良好的储存空间被广泛应用。

4.1 构建K-D树

K-D 树是一种树状数据结构，将实例点存储在k 维空间中，便于快速检索，主要应用于多维空间关键数据的搜索（如：范围搜索和最近邻搜索）。K-D 树是二进制空间分割树的特殊的情况，其基本原理是根据某一维度的值确定的超平面将原k 维空间分割成两个k 维子空间，而这两个子空间里的点分别构成根节点的两棵子树[2]，K-D 树的三维空间构建模型如图13所示。

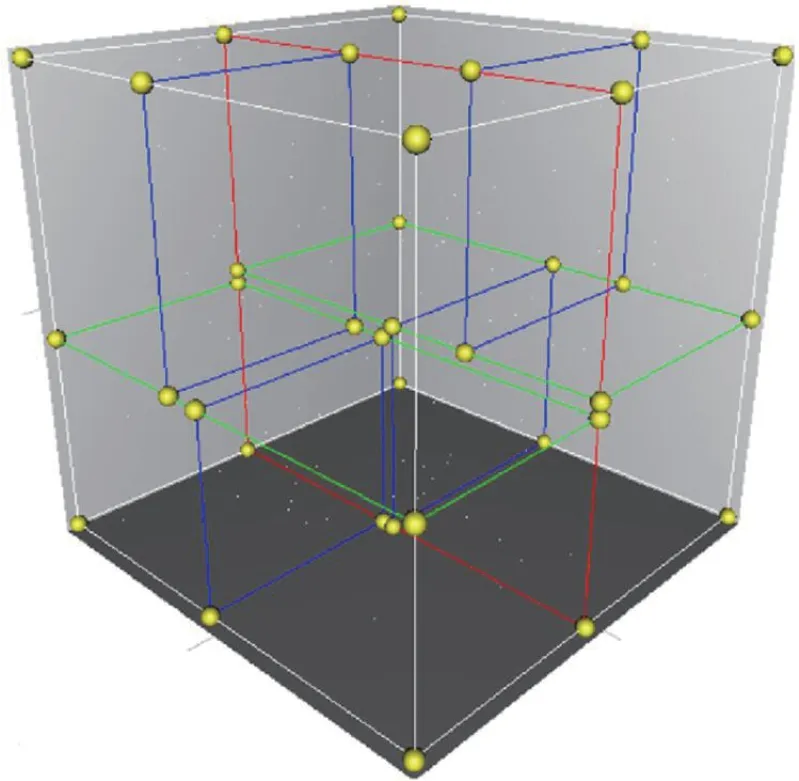
图13：K-D 三维空间模型

图中红色线部分就是沿着红色线轴做个垂直分割面，同理，绿色和蓝色也是根据其颜色线做垂直分割面，其实K-D 树就是在三维平面XYZ 三个轴上轮流做了一次二叉树。

K-D 树建树过程为：

（1）首先建立一个根节点；

（2）在X,Y,Z 三个轴上找出方差最大的值，其所在维度就作为分割数据的参考维度，这样就可以将所在维度的数据点分散开来，可以最大程度的保证K-D 树的平衡；

（3）将全部的数据点根据上述步骤中设置的参考维度进行排列，并选择位于中间的点，然后将中间点作为根节点，与分裂维度上所有的数据进行比较，比中值小的点划为左子树，比中值大的点划为右维度；

（4）构成的左子树和右子树中的数据点按照上述步骤分别再进行划分，直到所有数据都被建立到K-D 树的节点上为止。

自此，一个K-D 树就建立完成。

4.2 搜索最邻域

建立完K-D 树后，对于确定已知的数据目标点，我们利用K-D树来完成邻域搜索[3]。我们首先拿到根节点S1，因为目标节点的X值小于根节点，所以们搜索左边部分，来到S2 区域，目标节点的Y 值大于S2 故继续搜索S4 区域，我们一直搜索，直到找到最末端节点。此时最末点节点为g，我们以目标节点为圆心，以节点g 为半径画一个圆，此时我们已经找到了一个节点g，此节点为目标节点的最快距离，正是因为最快节点的存在所以我们可以直接跳过一些区域，提高运算效率，圆内的区域为最快区域。因为圆内与S4区域有交集，所以继续寻找S4 区域，S4 区域存在园内点e，且比最快距离要小，所以有可能是最近距离，故将圆半径变为e，此时的圆与S5 左边区域已无交集，故不在此区域进行搜索直接丢弃。来到S1 右边区域，直接搜索S6 部分，但交集部分无最末端节点，搜索结束。如图14、图15所示。

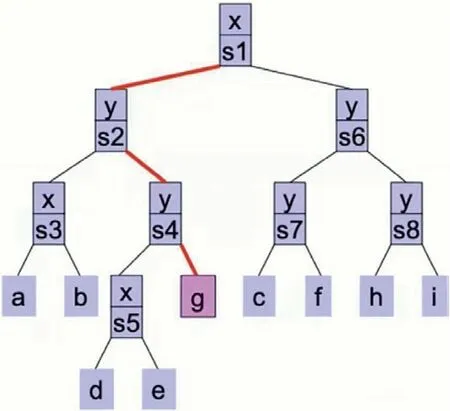
图14：K-D 树图

图15：最近距离图

利用K-D 树查找最近距离的流程为：

（1）在构建好的K-D 树中找出包含目标点的叶节点：从根结点出发，递归地向下访问K-D 树。若目标点当前维的坐标小于切分点的坐标，则移动到左叶子结点，否则移动到右叶子结点，直到子节点为叶节点为止；

（2）以目标点为圆心，以目标点到叶子节点样本实例的距离为半径，得到一个超球体，最近邻的点一定在这个超球体内部；

（3）归地向上进行回溯操作，在每个结点进行查询，检查另一个子节点包含的超矩形体是否和超球体相交，如果相交就到这个子节点寻找是否有更加近的近邻，如果有则以该实例点为“当前最近点”；

（4）持续查找，直到搜寻完所有节点。

本文利用基于半径查找最邻近的点，此方法半径是可以随着距离的变化而变化，所以比KNN 更容易实现。

5 结束语

本文针对不同平台搭建PCL 所需要的运行平台，结合配置中出现的错误提出了相对应的解决方法，给广大点云学者们提供了有效的数据参考。也针对海量数据集，结合开源C++点云库创建了K-D树的空间数据结构，实现了快速的邻域搜索。