铺缆船用电缆埋设犁整机拖曳力学分析
吴富生 吴占阳 王 赟 许素蕾
(上海振华重工(集团)股份有限公司 上海200125)
0 引 言
电缆埋设犁在铺缆船拖绳的作用下边挖沟边铺缆, 海底电缆埋设犁挖掘铺缆过程中受到铺缆船拖绳的拖曳力。目前,铺缆船在施工时,对于确定拖曳力大小和角度,更多起依靠施工经验,缺乏理论指导。郭飞和李经纬研究了基于悬链线方程的海上横向补给高架索静态受力情况,为研究悬链式受力提供了理论参考。张太佶和胡晓为研究了海底电缆在敷设中的受力分析,为悬链式缆绳受力进行理论研究。但由于铺缆拖曳钢丝绳与电缆受力情况不同,不能将电缆悬链受力工况直接应用到铺缆钢丝绳。本文从埋设犁整机受力分析得到埋设犁所需的拖曳力大小和合理角度;在此基础上,利用悬链线公式和力学原理,推导出拖绳各项参数;并通过表格和曲线图分析拖绳各项参数变化趋势。为合理选用拖绳和合理选取参数提供了理论方法。
1 埋设犁整机受力分析
1.1 埋设犁受力模型
埋设犁在海底挖沟铺设电缆时,主要受力包括:自身重力、浮力、水流力(含粘性阻力)、滑靴支撑力、滑靴摩擦力、犁刀支撑力、犁刀摩擦力、拖绳拖曳力和挖掘阻力。其中,为建模方便,拖曳力分解为水平拖曳力和竖直拖曳力;挖掘阻力分解为水平挖掘阻力和竖直挖掘阻力(因整机主体钢结构全部为非密封中空结构,为简化计算,近似认为重心与浮心相同)。
如图1所示,根据力学平衡原理,水平和竖直方向合力均为0,若以整机重心为支点,则力矩合成为0(假设绕重心逆时针力矩为正);拖曳钢丝绳与水平方向夹角定义为α
,得到力学平衡公式以非齐次矩阵方程表示如下:
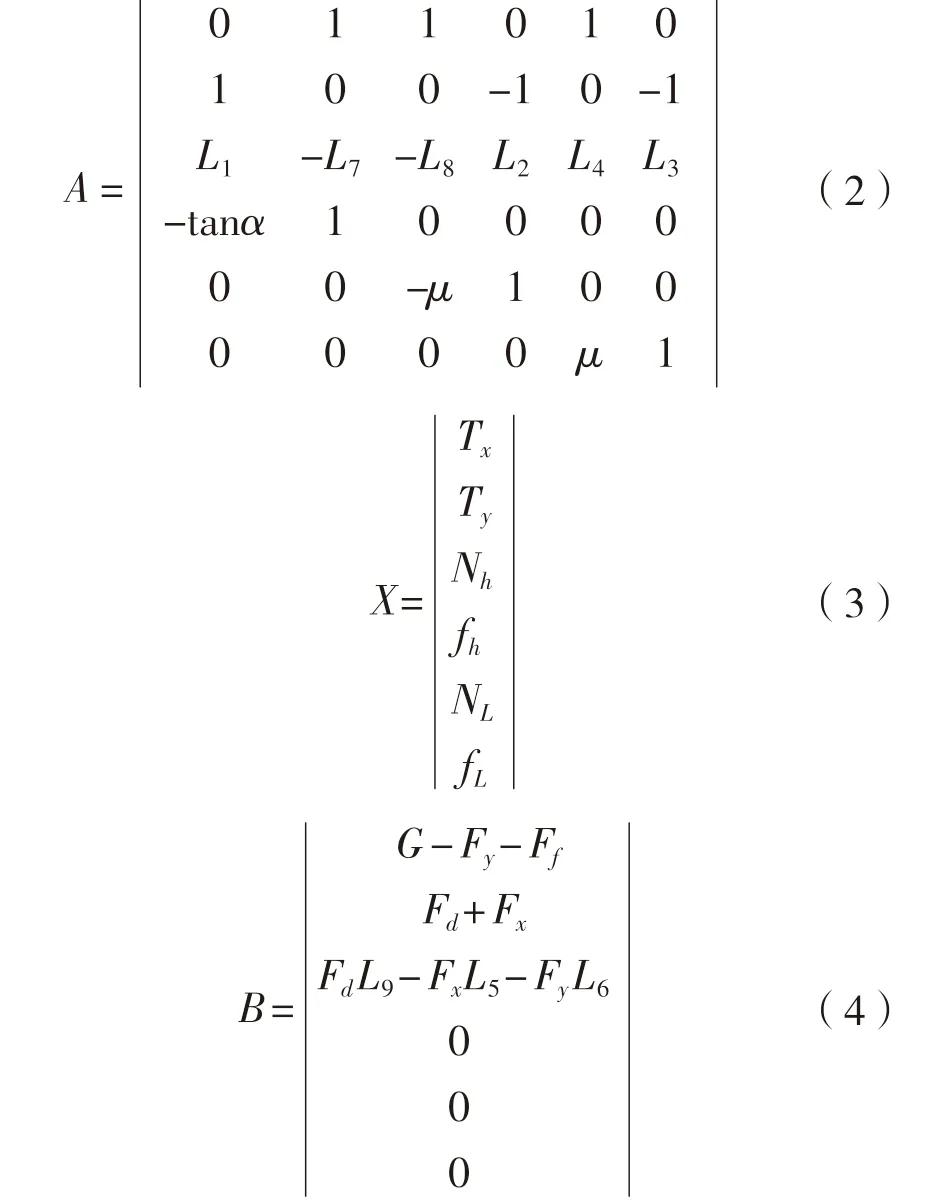
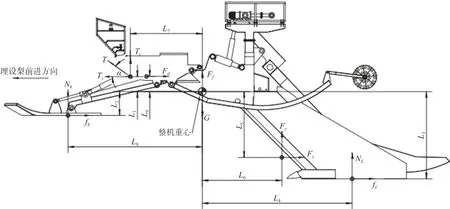
图1 埋设犁整机受力示意图
其中:上述方程式中:T
为水平拖曳力即埋设犁拖曳力T
的水平分力,kN;T
为竖直拖曳力即埋设犁拖曳力T
的竖直分力,kN;G
为埋设犁自身重力,kN;F
为埋设犁受到的水下浮力,kN;F
为埋设犁受到的水流力,kN;F
为埋设犁水平挖掘阻力,kN;F
为埋设犁竖直挖掘阻力,kN;N
为埋设犁滑靴支撑反力,kN;f
为埋设犁滑靴摩擦力,kN;N
为埋设犁犁刀体支撑反力,kN;f
为埋设犁犁刀体摩擦力,kN;α
为拖绳水平夹角即埋设犁犁拖曳力T
与水平方向的夹角,°
;μ
为埋设犁与土壤间摩擦系数;L
~L
为埋设犁各受力点到埋设犁重心位置的垂直距离,mm。1.2 埋设犁整机受力分析
以某型埋设犁在最大挖深工况下受力情况为实例,进行埋设犁整机受力分析。图1中,水平方向定义与埋设犁行进方向的反方向为正方向;竖直方向定义垂直向上方向为正方向。上述公式(1)~(4)中,L
~L
、拖绳水平角α
为已知数据,水平和竖直挖掘阻力F
、F
根据摩尔-库伦理论和土的极限平衡条件进行理论计算,水流力F
根据莫里森公式和水流粘性阻力原理,通过CFD软件计算得到,海水浮力F
和埋设犁重力G
通过三维建模得到,限于篇幅,此处不再赘述。所获得的数据见表1。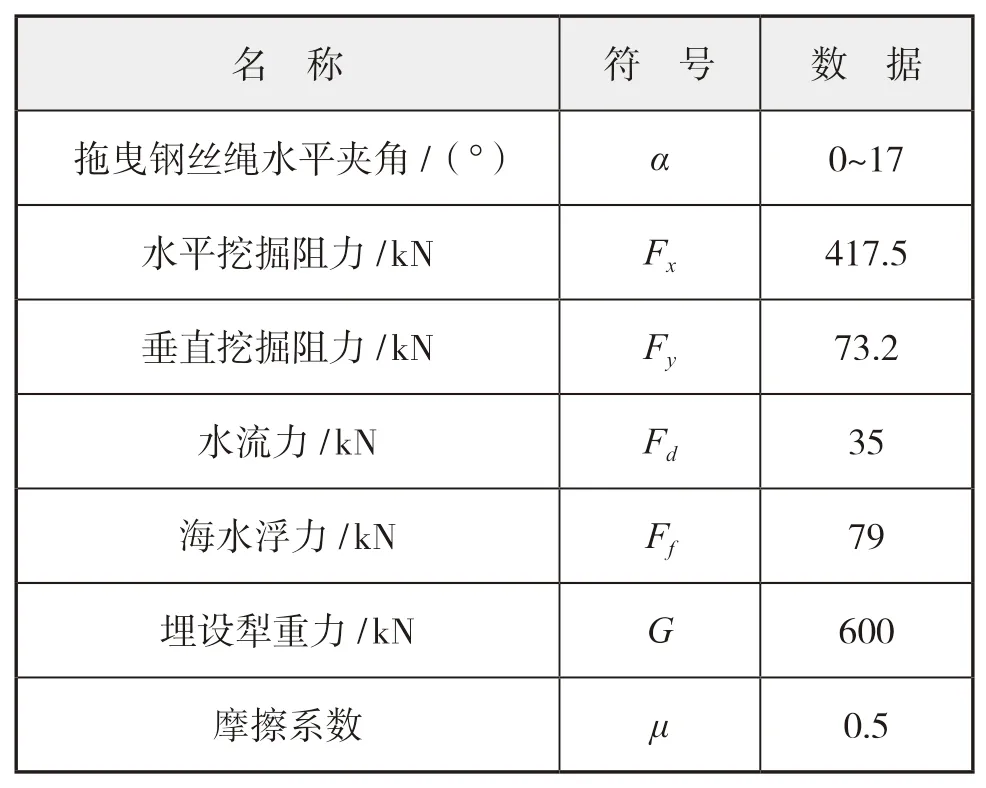
表1 某型埋设犁整机受力已知数据
将这些数据代入上述式(1)~(4),用Matlab软件计算得到数据如表2所示。
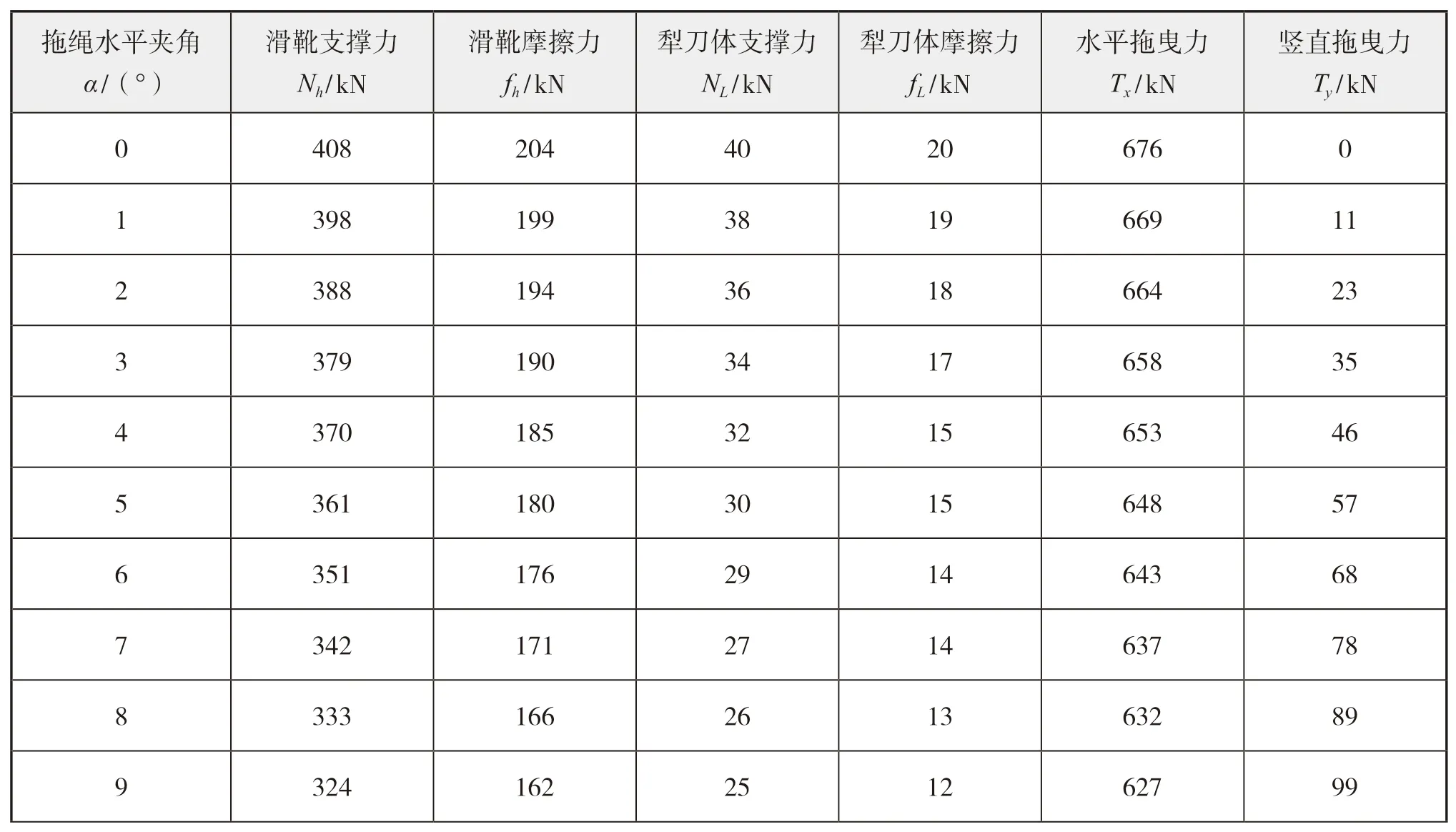
表2 埋设犁受力计算结果
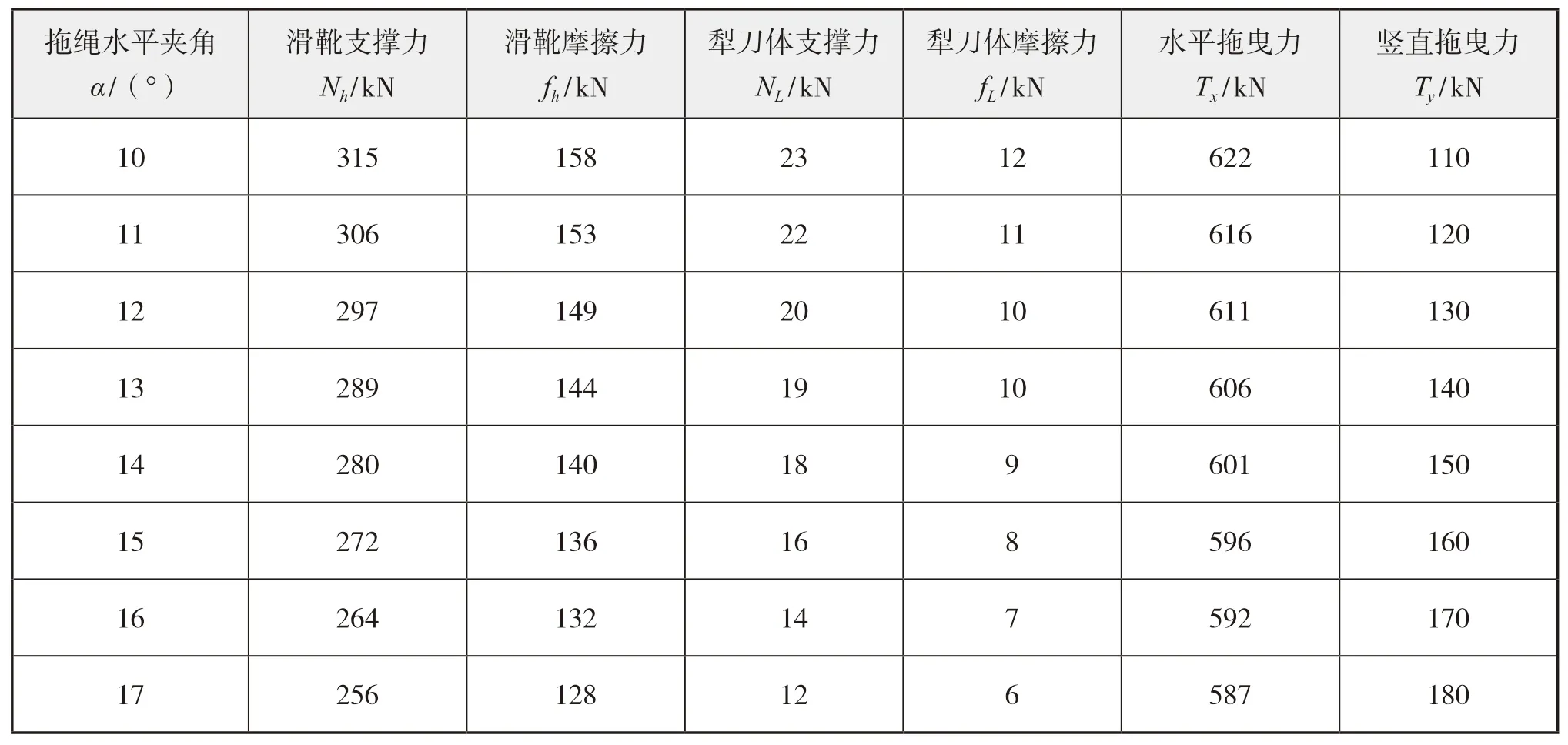
续表2
从表2可知,随着拖绳水平夹角α
的变化,相应的计算结果呈现一定的变化。为更清晰得到拖绳水平夹角α
对埋设犁各个作用力的影响,我们根据表2的计算结果,得到如图2所示的数据曲线。当埋设犁拖绳水平角α
从0°
逐渐增大时,除了竖直拖曳力逐渐增大外,其余受力均是逐渐减小。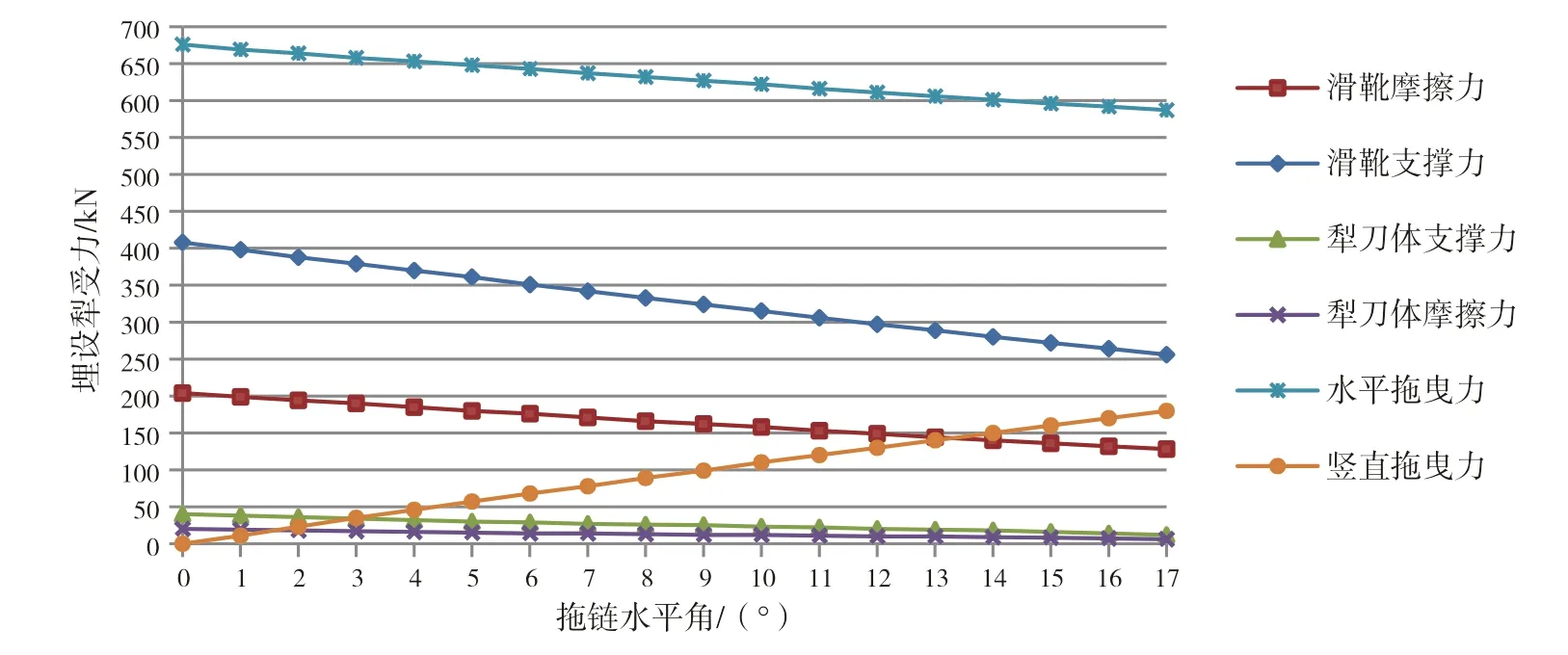
图2 埋设犁受力变化曲线图
埋设梨受力变化曲线如图2所示。图2可知,当拖绳水平夹角增大时,埋设犁后端犁刀体支撑力逐渐减小且趋于0。为了使埋设犁能有效挖沟,理论上埋设犁后端犁刀体支撑力需大于0。根据图2,可以得出结论:为了保证埋设犁有效挖沟,埋设犁拖绳水平角范围定义在0°
~15°
较为合理,且在此水平拖绳角度范围内,埋设犁都不会发生前倾或后仰,保证了埋设犁的整机稳定性。2 埋设犁拖绳受力分析
2.1 埋设犁拖绳受力模型
埋设犁是在铺缆船拖曳下进行挖掘工作,埋设梨拖绳受力如下页图3所示。
在埋设犁与铺缆船之间用拖绳相连接,拖绳在O
点与埋设犁连接,在B
点与铺缆船连接。拖绳两端分别与埋设犁O
点水平方向成一定夹角α
和船尾B
点水平方向成一定夹角β
。图3中以埋设犁与拖绳连接点O
为坐标原点。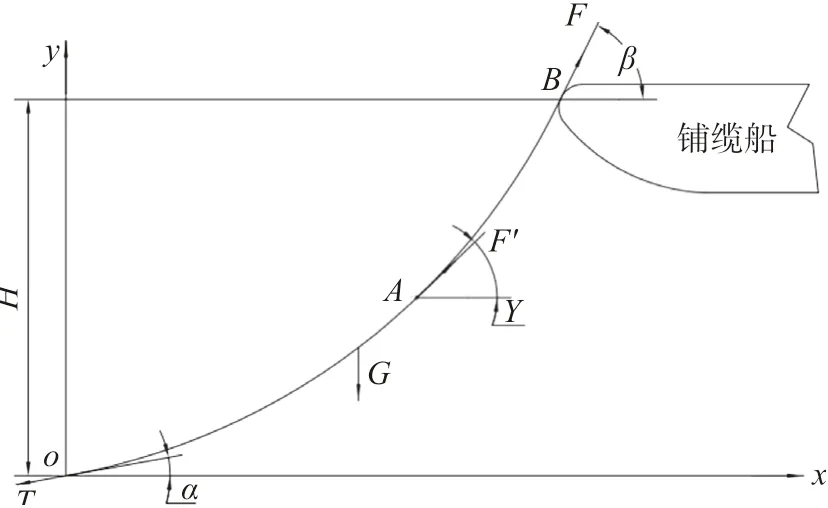
图3 埋设犁拖绳受力示意图
根据力学平衡原理,可以得到:
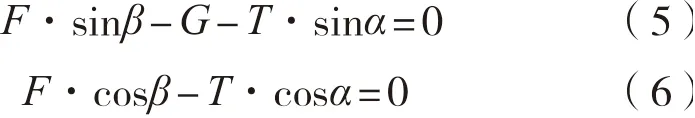
根据前面所述可知,上述公式(5)~(6)中:

T
为埋设犁O
点拖曳力,kN;F
为拖绳在船尾入水点B
处所受的拉力,kN;G
为拖绳水中自身重力,kN;α
为拖绳水平夹角,即埋设犁犁拖曳力T
与水平方向的夹角,°
;β
为铺缆船B
点处拖绳拉力与水平方向夹角,°
。2.2 埋设犁拖绳受力计算
如图3所示,在拖绳O
点和B
点之间任一位置取一点A
,分析拖绳在A
点位置受力情况,为分析拖绳点A
处的受力情况,现将图3中拖绳从点O
到点A
处的拖绳单独分析,受力情况显示如图4所示,其中G′
为拖绳从点O
到点A
处的重力。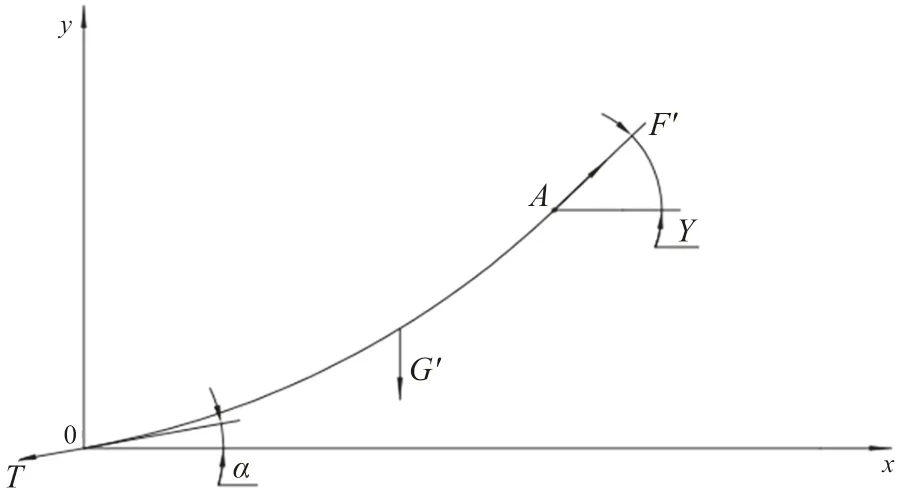
图4 拖绳点A处受力示意图
在图4中,根据力学平衡条件,得到如式(9):

F′
为拖绳任意点A
处所收拉力,kN;γ
为拖绳任意点A
处所收拉力与水平方向夹角,°
;得到:

α
<γ
<β
,根据式(6)和式(10),可知: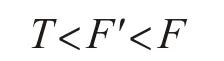
O
到点B
处,拖绳在点B
处受到的拉力F
最大。要计算拖绳在点B处的拉力F
的大小,必须要求出β
。埋设犁拖绳可以视为悬链形式,根据悬链线方程,可以得到如式(11):
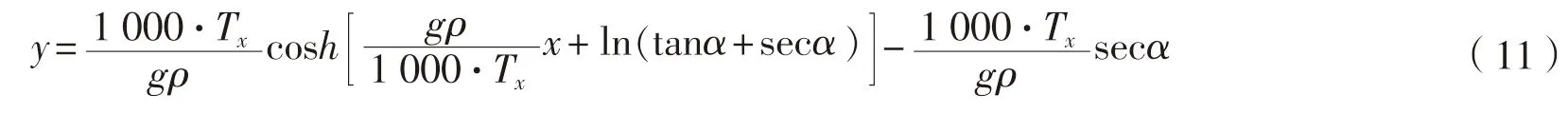
g
为重力加速度,取9.8 m/s;ρ
为拖绳在水中单位质量,kg/m;y
为水深,m;x
为埋设犁拖绳连接点O
到拖绳在船尾受力点B
的水平距离,m。在既定水深为H
情况下,图3拖绳点B
处,公式(11)中y
=H
,代入公式(11)经过求解得到点O
到拖绳在船尾受力点B
的水平距离x
,单位为m: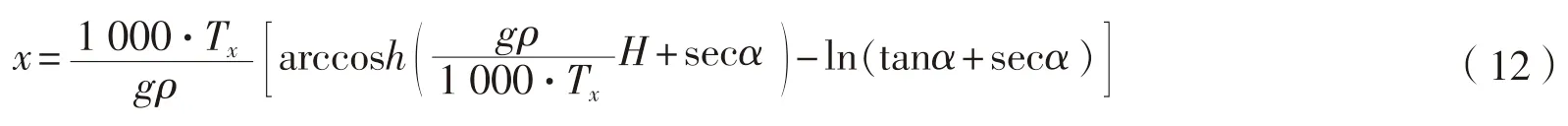
B
点斜率为:
且由式(11)可得到:
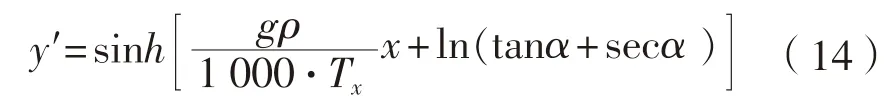
联立公式(12)~(14),求解得到:
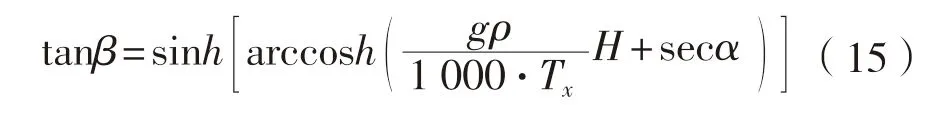
β
<90°
,所以根据三角函数性质,由式(15)可得到: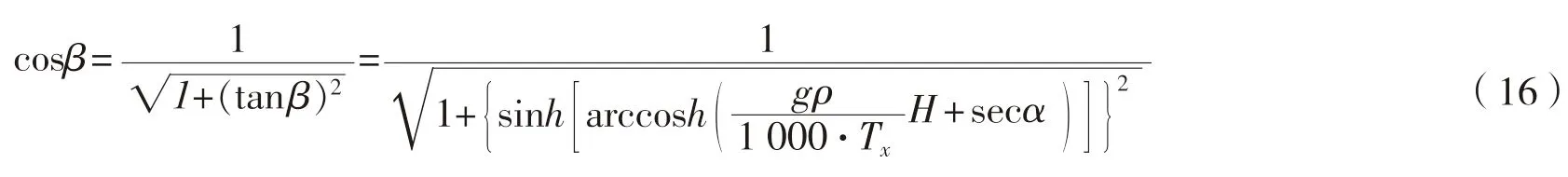
B
的拉力F
,单位为KN: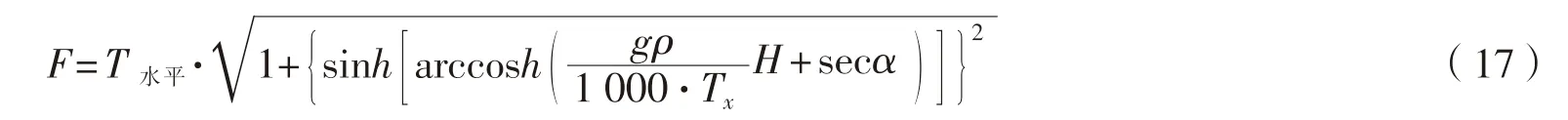
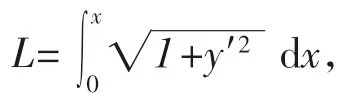
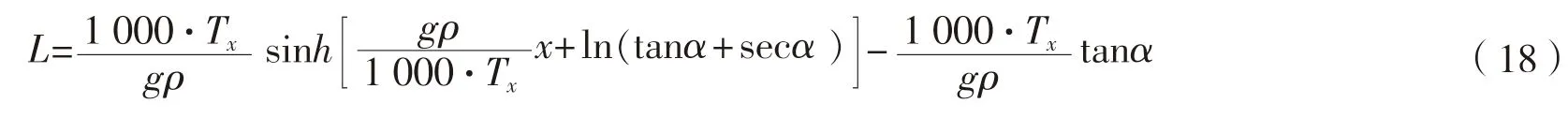
将式(12)代入式(18)中,得到埋设犁拖绳长度公式如下,单位为m:
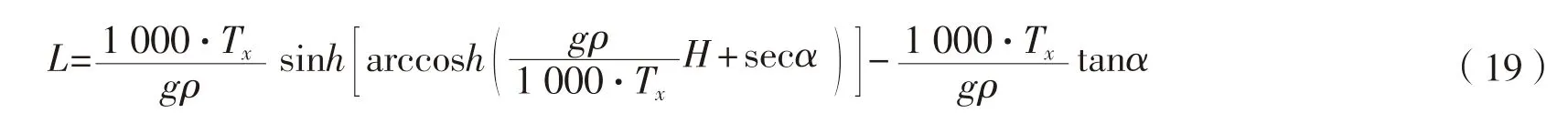
2.3 埋设犁拖绳受力分析
从上述埋设犁及拖绳受力情况分析可知:当埋设犁在最大挖深工况下,拖绳与埋设犁连接点O
处的拖绳水平夹角α
、拖绳的单位长度质量ρ
、工作水深H
,对拖绳在点B
处的受力F
、角度β
、长度L
和水平距离x
的取值大小有影响。根据前面表2的计算结果和公式(5)~(20),分别进行如下计算和分析:
(1)拖绳的单位长度质量ρ
、工作水深H
不变,拖绳水平夹角α
在0°
~15°
范围内对拖绳各参数的影响。如表3所示。
表3 埋设犁拖绳参数计算表(ρ = 10 kg/m,H = 500 m)
(2)拖绳水平夹角α
、工作水深H
不变,拖绳的单位长度质量ρ
变化对拖绳各参数的影响。如下页表4所示(为表达各参数变化趋势,仅以α
=0°
为例进行计算)。(3)拖绳水平夹角α
、拖绳的单位长度质量ρ
不变,工作水深H
变化对拖绳各参数的影响。如下页表5所示(为表达各参数变化趋势,仅以α
= 0°
为例进行计算)。为了更清晰分析各变化参数对埋设犁拖绳的影响,将上述表3、表4和表5以曲线图形式表示,如下页图5、图6和图7所示。分别以拖绳水平角α
、拖绳单位长度质量ρ
、埋设犁工作水深为变量,得到拖绳对应水平距离x
、拖绳长度L
和拖绳在点B
处的最大拉力F
的变化趋势。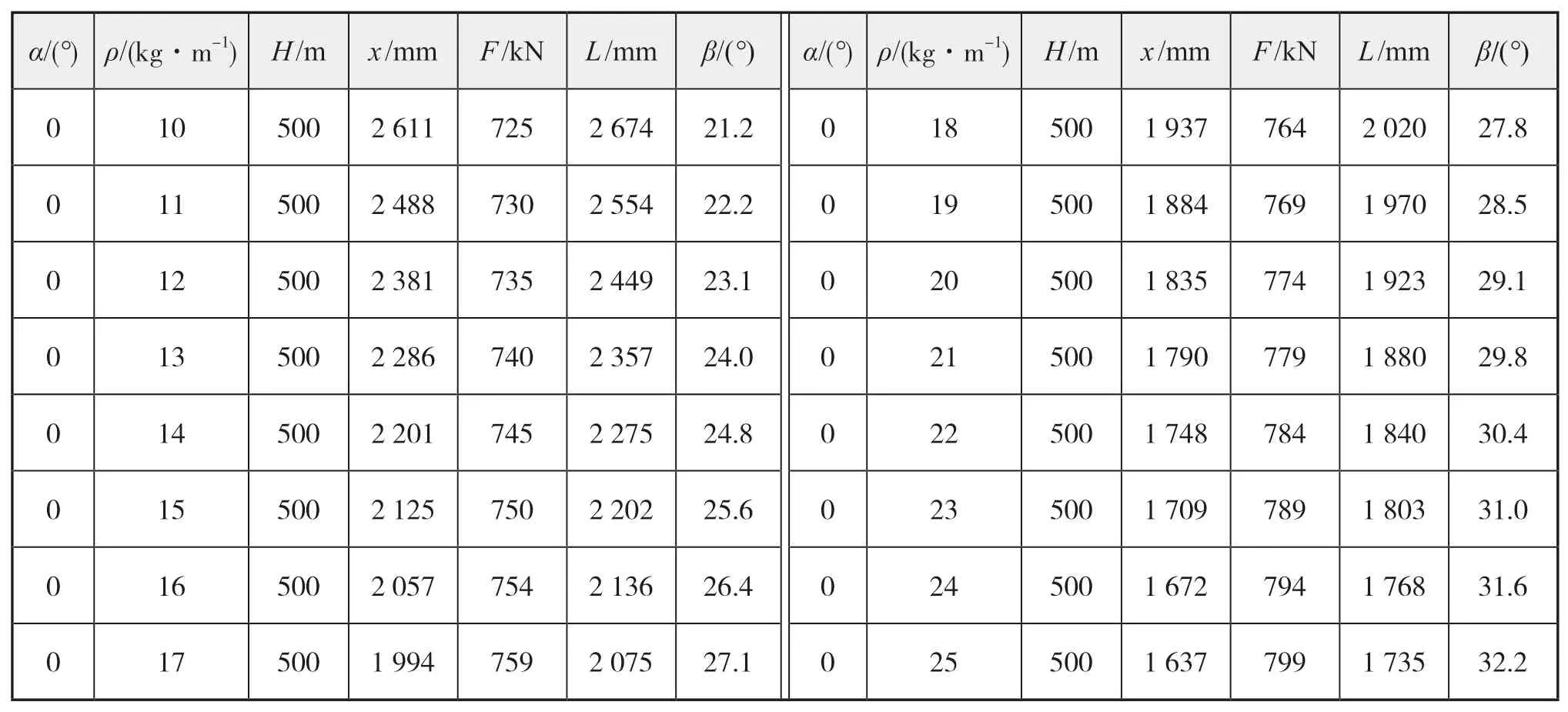
表4 埋设犁拖绳参数计算表(α = 0°,H = 500 m)
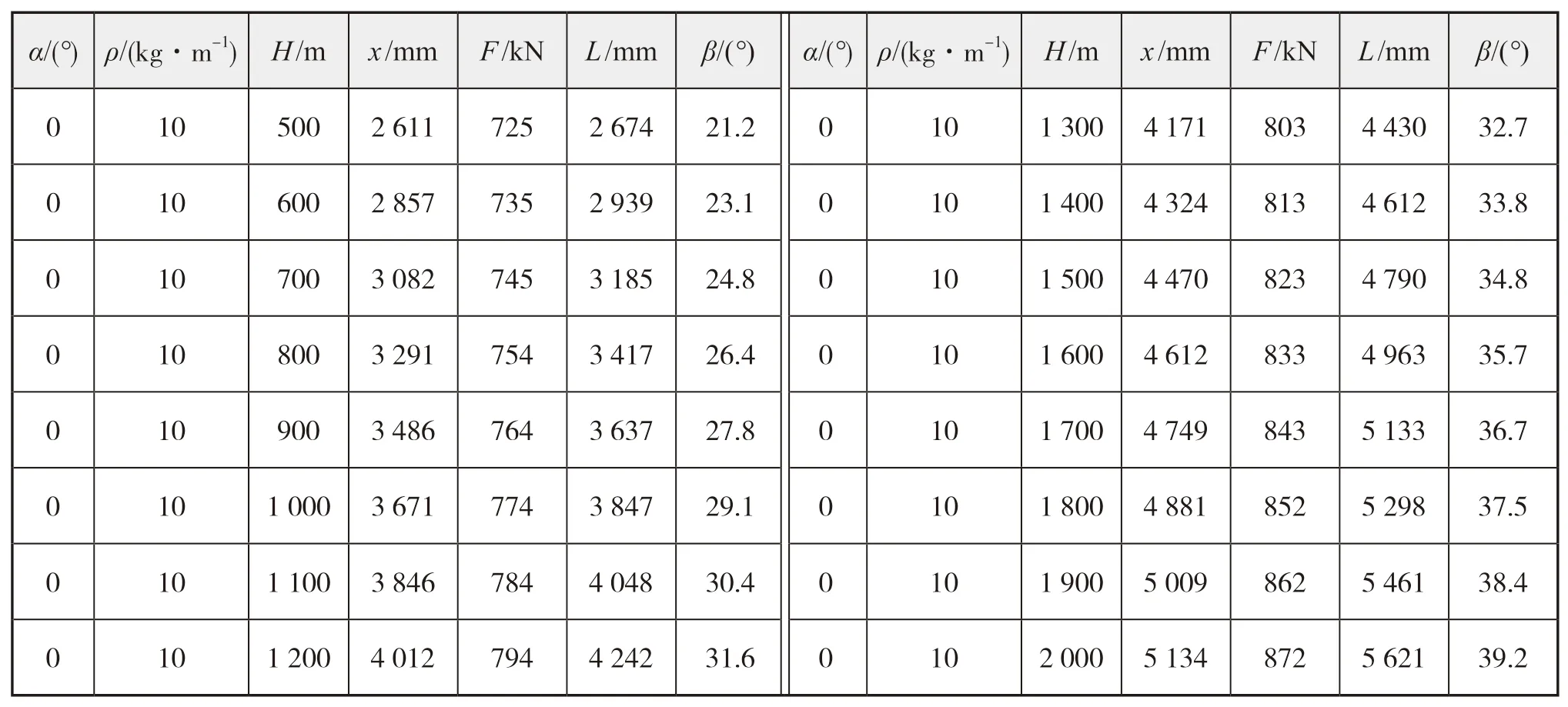
表5 埋设犁拖绳参数计算表(α = 0°,ρ = 10 kg/m)
根据表3、表4和表5的数据,结合图5、图6和图7综合分析,可得到如下结论:
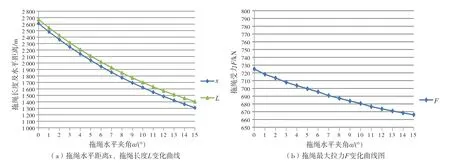
图5 埋设犁拖绳参数随拖绳水平夹角α变化曲线图:ρ = 10 kg/m,H = 500 m

图6 埋设犁拖绳参数随拖绳单位质量ρ变化曲线图:α = 0°,H = 500 m
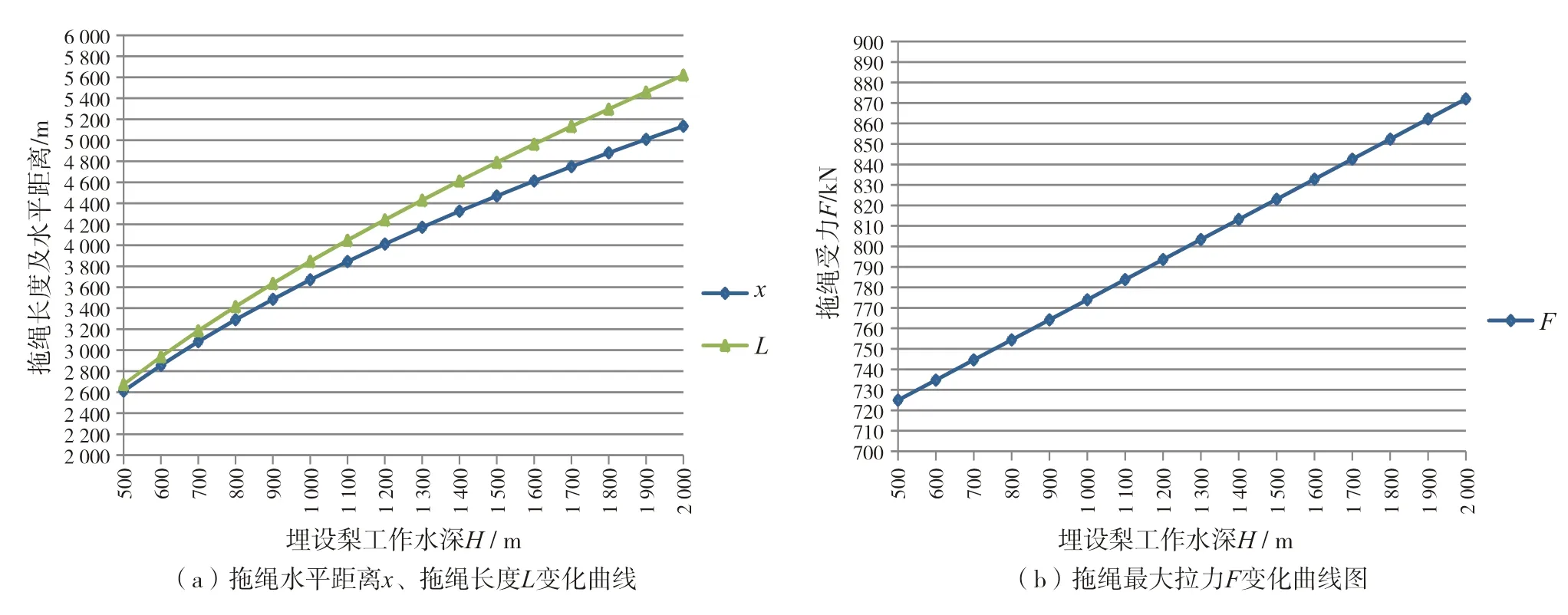
图7 埋设犁拖绳参数随工作水深H变化曲线图:α = 0°,ρ = 10 kg/m
(1)在拖绳单位质量ρ
、埋设犁工作水深H
不变情况下,随着拖绳水平夹角α
的增大,埋设犁与铺缆船的水平距离x
、拖绳长度L
和拖绳所受最大拉力F
均逐渐减小,同时拖绳在船尾的入水角度β
逐渐增大。但结合前述埋设犁整机受力分析可知,为保证埋设正常挖掘和稳定性,并不意味着拖绳水平夹角α
越大越好,在0°
~15°
范围内比较合适。(2)在拖绳水平夹角α
、埋设犁工作水深不变情况下,随着拖绳单位质量ρ
的增大,埋设犁与铺缆出的水平距离x
、拖绳长度L
逐渐减小;拖绳所受最大拉力F
和拖绳在船尾的入水角β
逐渐增大。这样在保证拖绳强度条件下,尽量选取单位质量小的拖绳。(3)在拖绳水平夹角α
、在拖绳单位质量ρ
不变情况下,随着埋设犁工作水深H
的增大,埋设犁与铺缆出的水平距离x
、拖绳长度L
、拖绳所受最大拉力F
和拖绳在船尾的入水角β
均逐渐增大。这样随着埋设犁工作水深的不同,可根据需要合理更换拖绳,以保证拖绳强度要求。3 结 语
本文根据力学平衡原理,通过对某型电缆埋设犁在既定工况下的整机受力分析,得到埋设犁在保持正常挖掘和稳定性前提下其受力状况和需满足的拖曳力大小,并在此基础上确定拖绳在埋设犁作用点的合理水平夹角;同时,结合拖绳在水中工作时的受力模型,用悬链方程推导出拖绳与铺缆船距离、拖绳长度、拖绳所受最大拉力和拖绳在船尾入水角度;并运用表格和曲线图,具体分析在不同条件下,拖绳各参数的变化趋势。本文为拖绳合理选型及合理调节埋设犁与铺缆船距离以及拖绳在船尾入水角度等数据提供了理论指导方法。

