中央扣对人行悬索桥抗风性能的改善

王宜航 周丹丹

摘 要：以国内某山区人行悬索桥为研究对象，针对其柔度大，抗风性能差的特点，利用有限元软件分析了增设中央扣以及不同中央扣布置方案对结构抗风稳定性的改善效果。研究结果表明：增设中央扣，提高了结构整体刚度，而且不同类型的设置方式，对主梁约束作用不一样，对结构抗风稳定性的提高有所差异，刚性比柔性中央扣对结构抗风稳定性的改善更有利，其中，单联刚性中央扣对结构抗风最有利。

关键词：人行悬索桥;柔度大;中央扣;抗风性能

中图分类号：U448.25文献标识码：A

0 引言

本文结合工程实例，借助有限元分析软件建立了空间结构模型，然后在主跨跨中分别布置单联、三联、五联柔性和刚性中央扣，通过研究设置中央扣对结构扭转刚度的改变，来分析中央扣对所研究的人行悬索桥抗风稳定性的改善效果，同时对比了柔性和刚性中央扣及其布置方式在改善效果方面存在的差异性。

1 研究背景

人行悬索桥自重轻、结构柔，抗风稳定性差，在极端大风环境中容易发生失稳现象。近年来，国内外专家学者针对悬索桥抗风措施进行了大量研究，并取得了一些成果。白桦等[1]通过数值计算和风洞试验研究了45°抗风缆、一联中央扣、降低矢跨比等抗风措施对国内某人行悬索桥抗风性能的改善效果。葛耀君[2]通过有限元分析和节段模型风洞试验探讨了润扬长江大桥和舟山西堠门大桥的颤振性能及其控制措施。何晗欣等[3]通过有限元计算和风洞模型试验，分别研究了抗风缆、桥面开孔、中央扣等抗风措施对新疆赛吾迭格尔大桥颤振性能的改善。廖海黎等[4]研究了固定翼板和主动控制翼板，结果表明，附设空气动力扰流板可以有效改善悬索桥抗风稳定性。陈政清等[5]研究了舟山西堠门大桥长细吊索风振问题抗风减振方法。巩明等[6]利用ANSYS有限元软件通过不断迭代的方法研究了某人行悬索桥主缆及抗风缆找形方法，对其设置抗风缆后有效改善了该悬索桥抗风性能。宋锦忠等[7]探讨了改善桥梁抗风性能的几种气动措施及其作用机理。姜天华[8]从空气动力学措施、机械措施、结构措施三方面，针对大跨度桥梁抗风措施数十年来的研究进展，进行了系统性回顾。

2 工程背景

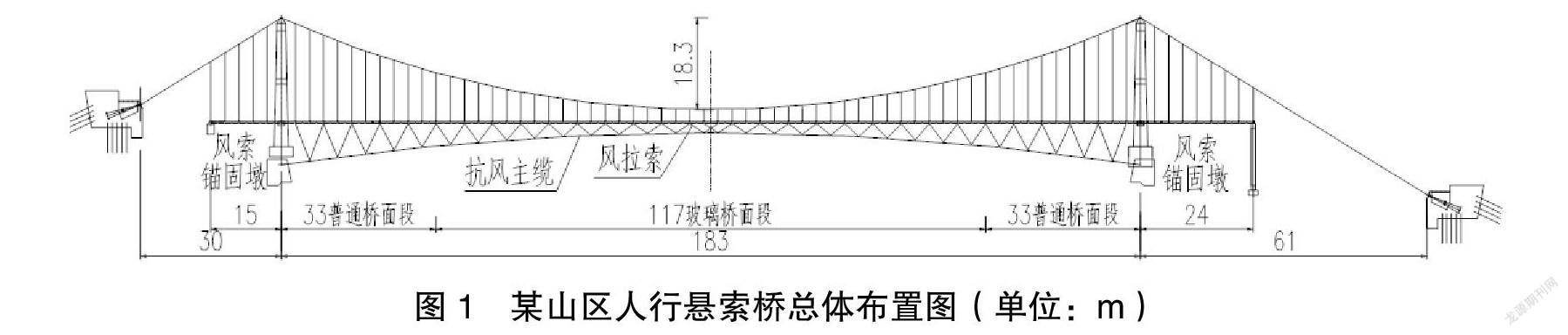
某山区人行悬索桥，结构形式双塔三跨，桥跨布置（30+183+61）m，桥面宽4.4 m。加劲梁采用纵横梁体系，由纵梁、横梁、斜撑连接而成，材料均为Q345钢，按每3 m为一个标准节段，与吊杆相连。吊杆钢丝绳Φ40 mm，材料为Wire 1 770，吊杆间距顺桥向3 m。空间索面主缆垂跨比1/10，塔顶处间距6.0 m，跨中处间距4.4 m，材料为Φ50 mm的ZAA6-37WS-IWR1870钢丝绳，每根索布置7根平行钢丝束。门架式桥塔为变截面结构，塔顶尺寸1 m×1.8 m，塔底尺寸1 m×3 m，按线性规律变化，为混凝土实心结构，高度25 m。总体布置见图1。

3 有限元模型建立

3.1 材料参数

结构模型材料参数取值见表1。

3.2 边界条件

不改变结构力学性能的同时，简化模型边界条件，具体处理方式见表2。在实际结构中，两桥塔下横梁位置处的加劲梁并不连续，因此，建模时将其分成三片，每片按照简支梁来考虑，边界条件处理为：一边固定，一边铰接。

（2）×：约束该方向自由度;○：放松该方向自由度;※：在刚性连接中约束该方向自由度。

3.3 模型建立

简化处理模型边界条件，确保实际结构的结构形式、设计要点两方面不发生改变。以中跨跨中的外侧点位作为坐標原点，依据材料、荷载参数，建立有限元空间结构模型。全桥模型如图2所示。

4 动力特性计算

借助Midas/Civil 2015有限元软件进行模态分析，采用一致质量矩阵模式，提取结构前10阶模态，前10阶频率值、振型分布特点见表3。

由表3计算结果，可以发现：

该人行悬索桥第一阶自振频率为0.245 2 Hz，表明结构柔度较大，侧向抗弯刚度较弱;结构正对称扭弯频率比（一阶正对称扭转频率与一阶正对称竖弯频率的比值）较低，数值为1.38，说明结构抗扭刚度弱，抗风性能差，需要对其采取抗风措施。

5 中央扣对抗风性能改善

5.1 中央扣布置方案

在主跨跨中分别布置单联、三联、五联柔性和刚性中央扣，以验证中央扣对所研究的人行悬索桥抗风稳定性的改善效果，同时比较柔性和刚性中央扣及其布置方式对该桥抗风稳定性的改善效果，工况一到工况六分别为：单联柔性中央扣、单联刚性中央扣、三联柔性中央扣、三联刚性中央扣、五联柔性中央扣、五联刚性中央扣，其中单联、三联、五联中央扣布置位置和布置形式如图3～图5所示。

5.2 不同方案抗风性能分析

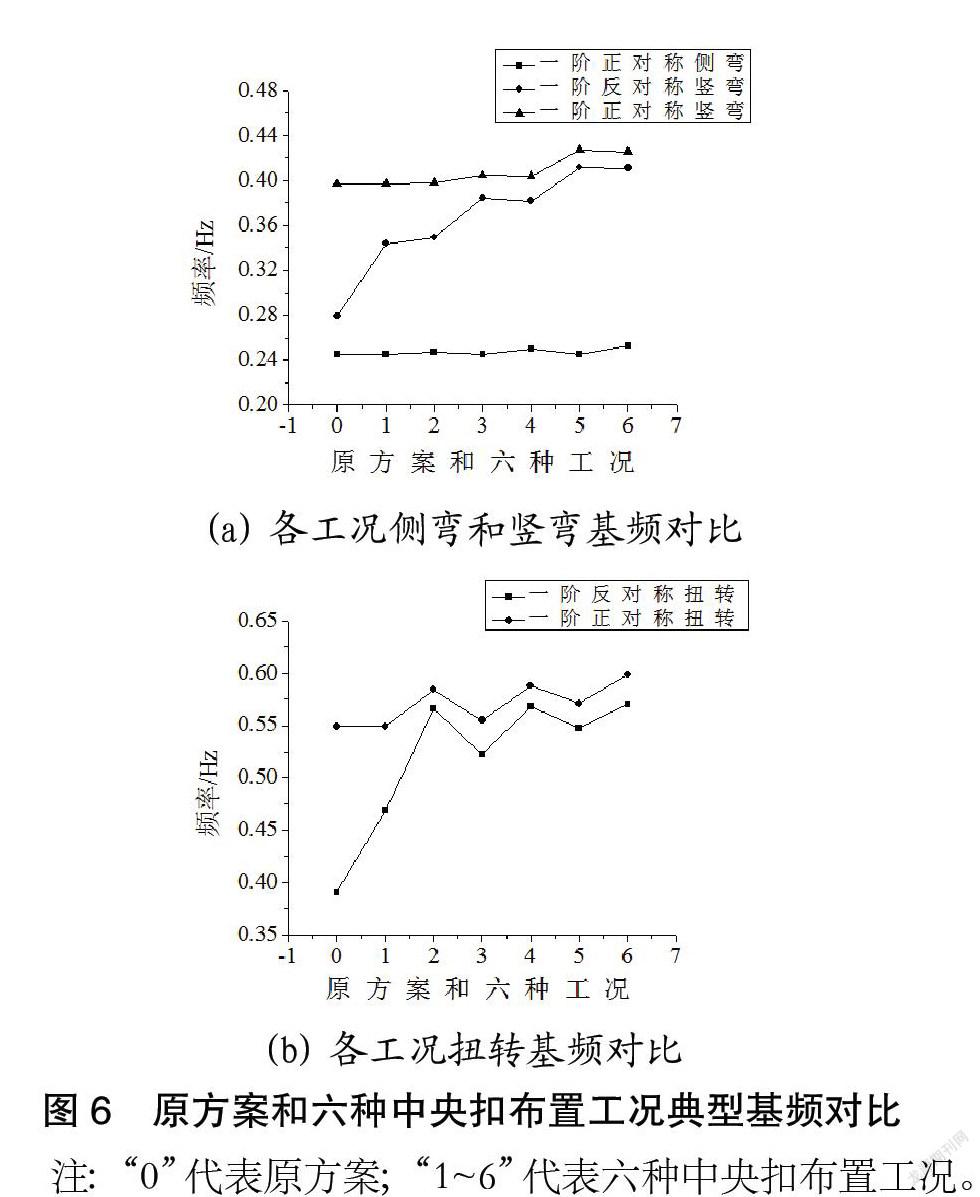
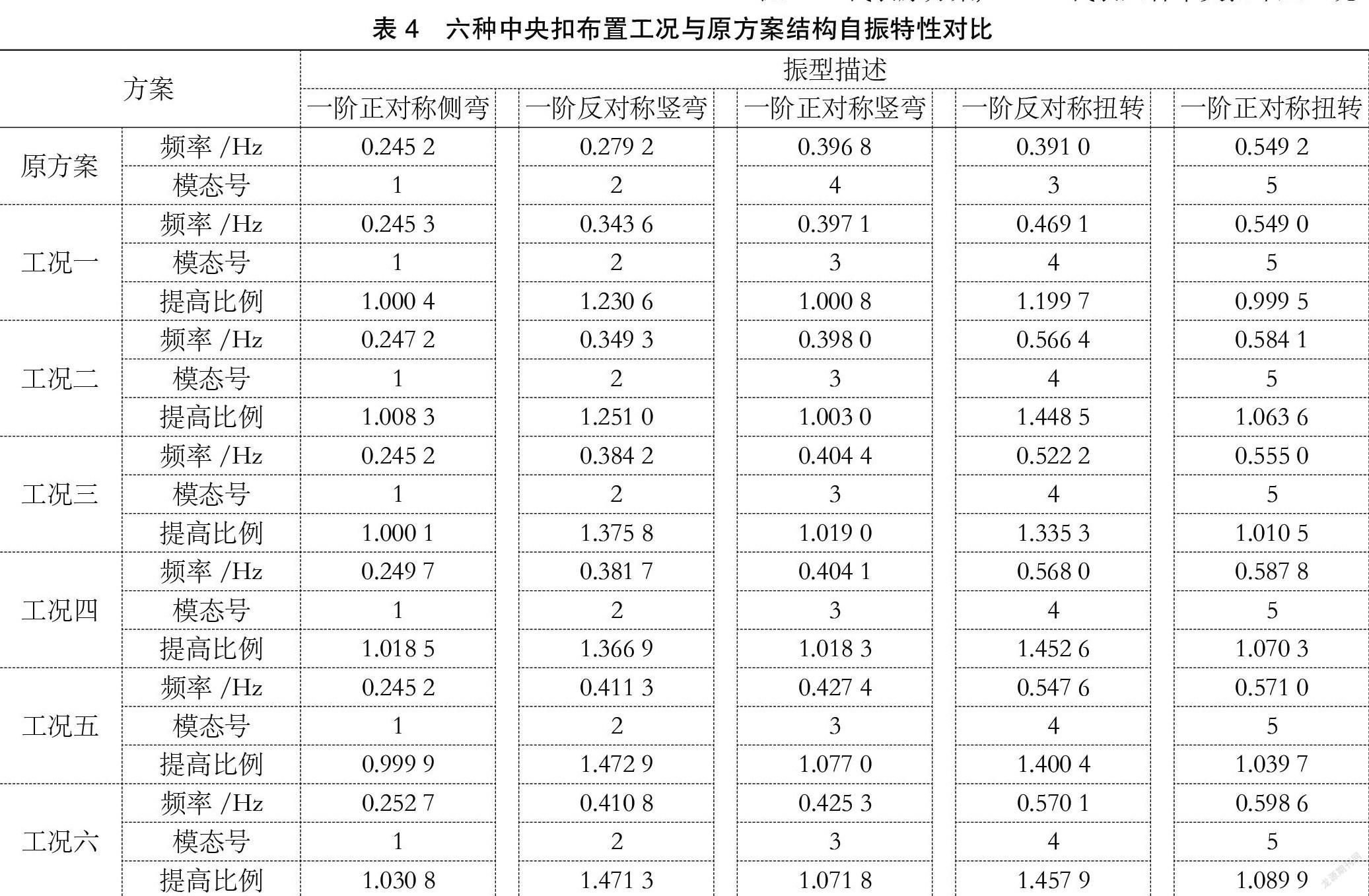
利用有限元软件计算并提取结构前30阶频率和振型，六种中央扣布置工况下结构自振特性与原方案对比见表4。原方案和六种中央扣布置工况典型基频对比见图6。

由表4和图6可知：

（1）增设中央扣较原方案而言，一阶反对称竖弯频率提高明显，工况一增加最少，增加23.1%，工况五增加最多，增加47.3%，且基本呈现上升趋势，原因在于中央扣使得主缆和加劲梁于跨中连接，起到限制纵向位移的作用，结构整体刚度因此得到提高。

（2）设置中央扣后，结构反对称抗扭刚度增加，一阶反对称扭转振型晚一阶出现，一阶反对称扭转频率较原方案增加明显，工况六增加最多，增加45.8%，工况一增加最少，增加20%。

（3）设置中央扣后，除工况一外，结构一阶正对称扭转频率略有提高，工况六提高最大，提高近9%。

（4）在低阶模态中，不同振型对中央扣敏感程度不一样，一阶反对称扭转振型最为敏感，一阶反对称竖弯振型次之，一阶正对称侧弯振型最不敏感。

（5）设置中央扣会使得结构频率有所提高，对结构抗风有利。而且，不同类型的设置方式，对主梁约束的作用不一样，对结构抗风稳定性的提高有所差异。

正对称扭弯频率比和反对称扭弯频率比能够正确反映出结构的抗风稳定性，二者取值越大，对结构抗风越有利。原方案和六种工况扭弯频率比见表5。原方案和六种工况扭弯频率比变化趋势见图7。

由表5和图7可知：

（1）工况二的正对称扭弯频率比和反对称扭弯频率比最大，工况五的正对称扭弯频率比和反对称扭弯频率比最小，表明工况二单联刚性中央扣对结构抗风最有利，同时节约材料。

（2）工况四的三联刚性中央扣正对称扭弯频率比和反对称扭弯频率比次之，工况六的五联刚性中央扣正对称扭弯频率比第三，反对称扭弯频率比略小于原方案，表明刚性中央扣相较柔性中央扣而言，对结构抗风稳定性的提高更有利，建议在提高人行悬索桥抗风稳定性时，相较柔性中央扣而言优先选用刚性中央扣。

6 结论

（1）增设中央扣的各工况结构一阶反对称竖弯频率和一阶反对称扭转频率明显提高，而且一阶反对称扭转振型晚一阶出现;在低阶模态，不同振型对中央扣敏感程度不一样。

（2）设置中央扣能够改善人行悬索桥抗风性能，并且不同的布置方式，提高效果不同，刚性比柔性中央扣在改善抗风性能上更有利，单联刚性中央扣改善效果相较而言最佳。

参考文献：

[1]白桦，李德锋，李宇，等.人行悬索桥抗风性能改善措施研究[J].公路，2012（12）：1-6.

[2]葛耀君.大跨度橋梁抗风的技术挑战与精细化研究[J].工程力学，2011（S2）：11-23.

[3]何晗欣，刘健新.大跨窄悬索桥抗风措施及其优化研究[J].公路交通科技，2010（3）：93-97+102.

[4]廖海黎，奚绍中.改善大跨度桥梁抗风稳定性的建议[J].国外桥梁，1999（3）：60-63.

[5]陈政清，雷旭，华旭刚，等.大跨度悬索桥吊索减振技术研究与应用[J].湖南大学学报（自然科学版），2016（1）：1-10.

[6]巩明，刘玉辉，张彦玲，等.基于ANSYS的人行悬索桥主缆及抗风缆找形方法研究[J].国防交通工程与技术，2018（5）：26-29+11.

[7]宋锦忠，林志兴，徐建英.桥梁抗风气动措施的研究及应用[J].同济大学学报（自然科学版），2002（5）：618-621.

[8]姜天华.大跨度桥梁风致振动控制研究[D].武汉理工大学，2009.