400 km/h高速铁路隧道洞口微气压波特征及其缓冲结构设计方法研究
胖 涛 杨伟超 王田天 罗禄森 何 洪
(1.中铁二院工程集团有限责任公司, 成都 610031;2.中南大学, 长沙 410083)
隧道洞口微气压波效应会对周边环境产生不良影响,严重时会造成隧道洞口附近玻璃等脆性构筑物破坏。自1964年日本东海新干线开通以来,国外学者对隧道洞口微气压波开展了大量研究,小沢[1]等研究了压缩波在隧道内板式无砟轨道传播压力变形的问题,建立了压缩波从隧道入口传播到出口产生微气压波之间的关系;Mashimo S[2]通过现场测试,对高速铁路隧道洞口微气压波的形成机制进行了深入分析,并指出隧道进口段形成的初始压缩波在出口端的辐射造成了洞口微气压波,且此微气压波的峰值与初始压缩波的变化速率直接相关。随着我国高速铁路的发展,国内学者针对350 km/h及以下速度的高速铁路隧道洞口缓冲结构进行了大量研究,宋军浩[3]等采用动模型试验对隧道壁面压力波和出口微气压波展开研究,得到了车头形状和车速对微气压波的影响规律;吴剑[4]等以隧道内的试验为根据,提出了考虑微气压波作用下的缓解率,并提出了对应的设计参数;Zhang[5]指出帽檐斜切式缓冲结构是减缓微气压波最有效的形式;黄兆国[6]研究了高速磁浮列车快速通过隧道时的气动特性,得到了阻塞比与微气压波的关系;陶伟明[7]研究了不同形式缓冲结构对微气压波的减缓效果;舒信伟[8]等对5种不同头型列车进行分析,得出增加流线型头部长度是减小气动阻力的有效途径,并可减缓洞口微气压波效应。
目前,国内对于高速铁路隧道洞口微气压波的研究主要是针对350 km/h及以下速度进行的,对400 km/h 速度条件下隧道洞口微气压波特征及其合理缓冲结构型式等问题的研究相对较少。本文对400 km/h 列车通过隧道时洞口的微气压波特征开展研究,并在此基础上提出合理的缓冲结构型式及其设计参数,相关研究成果可为新建400 km/h高速铁路或提速铁路隧道洞口缓冲结构的设计提供依据。
1 研究方法
本文基于FLUENT软件,采用三维可压缩动模型特征线数值方法,建立了隧道-列车-空气的气动仿真计算模型,分析400 km/h速度下的隧道洞口微气压波变化特征。同时,依据轨道交通安全教育部重点实验室的列车空气动力学效应动模型实验平台,开展 400 km/h及以上速度下的高速铁路隧道空气动力学动模型实验,采用模型试验、现场测试和数值模拟相结合的方法验证数值计算结果的可靠性。
1.1 计算理论基础
高速列车突入隧道时,列车周边及隧道之间的流场为三维、粘性、可压缩、非稳态湍流流场。本文选用RNGκ-ε湍流模型。
湍流动能k方程为:
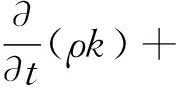
(1)
湍流耗散率ε方程为:
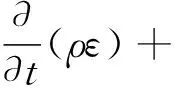
(2)
式中:υ——空气运动粘度,υ=μ/ρ;
υl——层流运动粘度;
υt——湍流运动粘度;
C1、C2、σk、σε——经验常数,参考近几年已发表的文献,本文计算时取C1=1.47,C2=1.92,σε=1.0,σε=1.33。
1.2 隧道及列车模型
为准确分析隧道洞口的微气压波变化特征,隧道和列车均以我国现行高速铁路的运行条件为基础进行实体建模,隧道选取100 m2和110 m2两种断面,其中,100 m2隧道断面严格按照现行350 km/h速度条件下双线隧道标准断面建模,110 m2隧道断面则在标准隧道断面的基础上,采用同比例放大的方法得到。由于隧道洞口微气压波峰值主要与初始压缩波的变化率有关,而初始压缩波的变化率则主要受隧道断面和列车车头长度影响,与列车编组数量的相关性并不显著。为提高计算效率,列车选取流线型较好的3节编组CRH380B型列车进行数值仿真,如图1所示。

图1 计算几何模型图
1.3 计算网格模型及边界条件
模型采用结构化网格和非结构化网格进行划分,隧道及两端大气部分采用结构化网格,缓冲结构区域采用非结构化网格。网格区域分为静止网格区域和动网格区域,动网格区域包括列车及附近空气部分,运用铺层法实现列车与隧道之间的相对运动。
列车表面网格及动网格区域内部的网格均设置为Ragid,即这部分网格会整体向前移动,不会出现网格重建和网格尺寸变化的情况。动网格两端设置成Stationary,保证动网格部分不会运动到边界以外。动网格与静网格部分通过Interface进行信息交换。两端大气设置成压力出口边界条件,地面、缓冲结构表面及隧道壁面为壁面。
1.4 数值仿真可靠性验证
为验证本文数值仿真结果的准确性,将计算结果与中南大学高速列车动模型试验结果进行对比,洞口外20 m处的对比结果如表1所示。
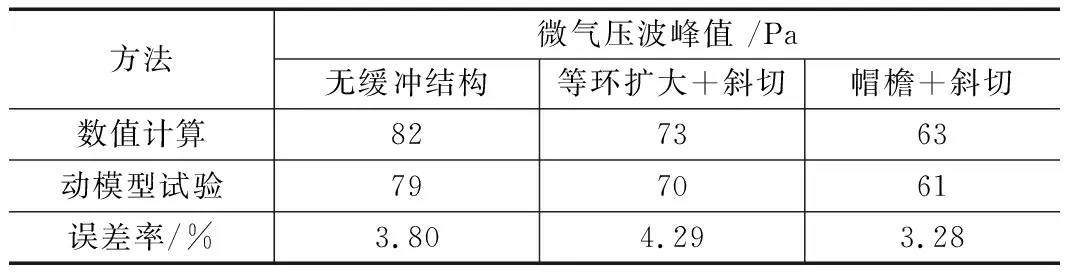
表1 计算结果与试验结果对比表
从表1可以看出,数值仿真结果的误差率不超过4.5%,且多工况的计算结果与试验结果均保持了很好的一致性,说明本文采用的数值仿真方法是正确的,模型的参数选取是合理的,仿真结果可靠。
2 400 km/h速度下洞口微气压波特征及其影响因素
以400 km/h速度的3节编组CHR380B列车在长 1 000 m、断面面积为100 m2的高速铁路隧道中运行为例,分析微气压波的变化特征。
2.1 洞口外微气压波峰值衰减规律
隧道出口外不同位置的微气压波变化时程曲线如图2所示,该计算工况下微气压波峰值随洞口外距离的衰减规律如图3所示。
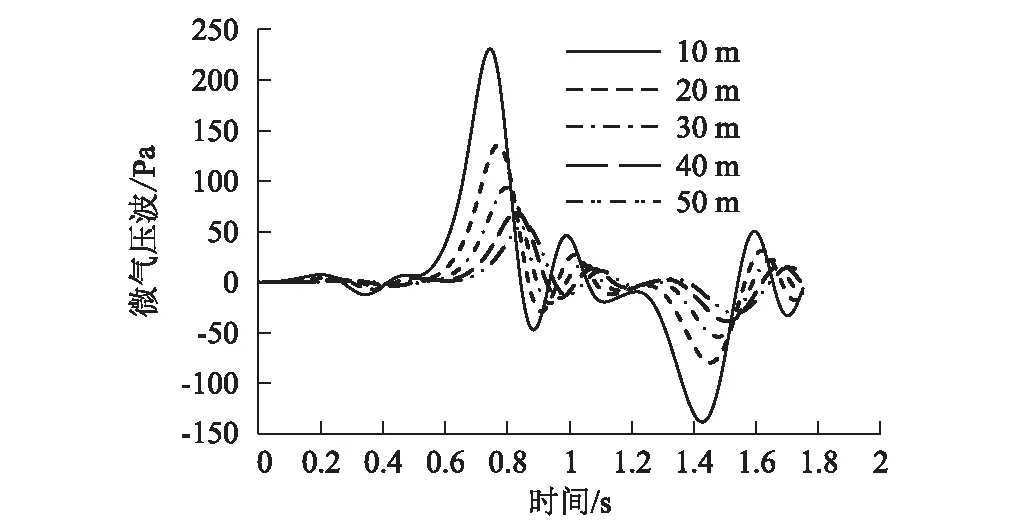
图2 隧道洞口微气压波时程曲线图
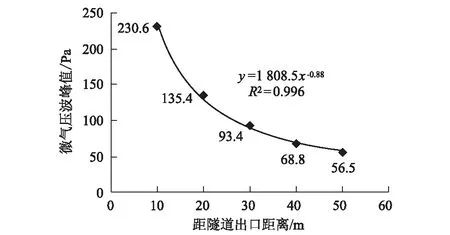
图3 微气压波峰值随洞口外距离的衰减规律图
从图2、图3可以看出:
(1)高速铁路隧道洞口微气压波随洞内压缩波的传播而不断变化,其中,压缩波使微气压波出现正峰值,膨胀波使洞口微气压波出现负峰值,而最大峰值则是由车头进入隧道进口时形成的初始压缩波引起。
(2)洞口微气压波峰值随距洞门出口距离的增大而迅速衰减,距出口10 m、20 m、30 m、40 m和50 m的微气压波峰值分别为230.6 Pa、135.4 Pa、93.4 Pa、68.8 Pa和56.5 Pa,微气压波峰值与距离的对应关系近似为y=1 808.8x-0.88。洞口微气压波不满足规范距洞口20 m和50 m处的微气压波分别小于 50 Pa和20 Pa的要求。
2.2 车速对微气压波的影响
列车速度是影响洞口微气压波的主要因素,本文对不同速度条件下隧道洞口20 m处微气压波峰值的变化进行对比。350 km/h和400 km/h速度下洞口20 m 处微气压波时程曲线如图4所示,车速与微气压波峰值之间的拟合曲线如图5所示,350 km/h和400 km/h 速度下隧道洞口微气压波峰值如表2所示。
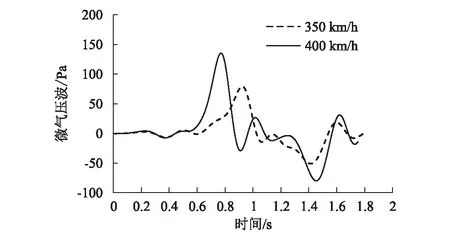
图4 隧道洞口微气压波时程曲线图
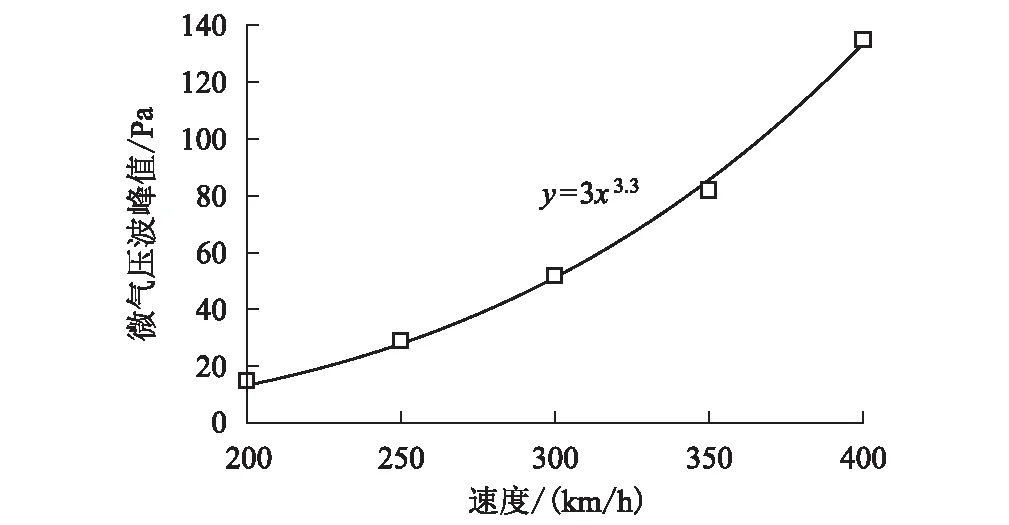
图5 列车速度与微气压波峰值之间的关系图
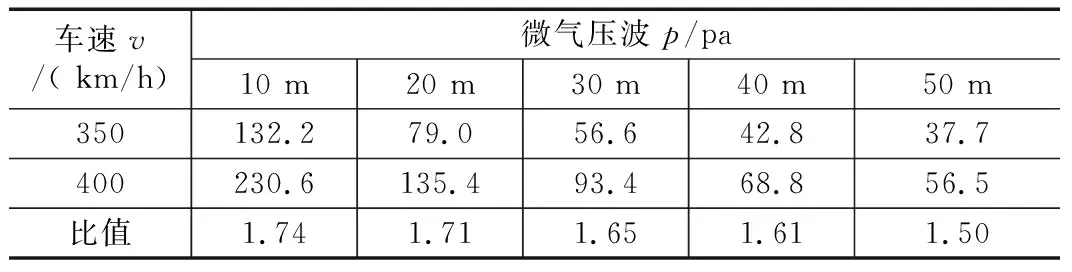
表2 隧道洞口微气压波峰值对比表
从图4、图5可以看出,受初始压缩波的影响,350 km/h 和400 km/h速度下隧道洞口微气压波均表现出压力突增、突降现象,且变化规律基本一致。当列车速度低于300 km/h时,隧道洞口20 m处的微气压波峰值均低于50 Pa,满足规范要求。当列车速度为300 km/h 和350 km/h时,微气压波峰值分别达到52 Pa 和79 Pa,均超过规范值,车速与微气压波峰值之间呈现超3次方(y=3x3.3)的正比关系,即当列车速度由 350 km/h 提升至400 km/h时,洞口微气压波峰值会出现大幅增加,洞口20 m处的微气压波峰值将由超出规范值约30 Pa增加到85.4 Pa,即超标率由58%增大到171%。洞口50 m处微气压波峰值由超出规范值约17.7 Pa增加到36.5 Pa,即超标率由89%增大到183%。
2.3 隧道长度对微气压波的影响
除了列车速度,隧道长度对微气压波也有一定程度的影响, 350 km/h和400 km/h两种速度条件下不同长度隧道洞口微气压波峰值对比如图6所示。

图6 不同隧道长度下隧道洞口微气压波峰值图
从图6可以看出:
(1)当列车速度为350 km/h时,隧道洞口微气压波峰值随隧道长度的增大而减小,二者呈负线性相关关系,隧道洞口20 m处和50 m微气压波峰值与隧道长度的拟合方程分别近似为y=-0.012 1x+90.86和0.004 2x+37.79,这一规律与参考文献[9]是一致。
(2)相反地,当列车速度为400 km/h时,隧道洞口微气压波峰值随隧道长度的增大而增大,二者呈正线性相关关系,隧道洞口20 m处和50 m微气压波峰值与隧道长度的拟合方程分别近似为y=0.017 7x+115.09和0.007 9x+47.65。
发生上述现象的原因可能在于:当列车速度由 350 km/h 提高到400 km/h时,对应的Ma由0.285提高到0.327,而根据空气动力学的基本分析理论,对于Ma>0.3的中亚音速流动,空气压缩热将逐渐显现,因此,针对400 km/h+速度条件下的隧道洞口微气压波有必要继续进行深入研究。
3 400 km/h速度下洞口缓冲结构设计
已有研究表明,洞口微气压波峰值与初始压缩波的变化梯度呈现5~8次方关系[10],而消减初始压缩波的方法包括改善车头流线型(主要是提高长细比)、降低列车速度、增大隧道断面和在洞口加设缓冲结构等,本文主要结合增大隧道断面和增设缓冲结构两种方法进行分析。
3.1 增大隧道断面
列车以400 km/h速度通过100 m2和110 m2两种隧道断面的微气压波峰值对比如图7所示。

图7 100 m2和110 m2隧道断面洞口微气压波时程曲线图
从图7可以看出,对于400 km/h的高速铁路隧道,当隧道断面由100 m2增大到110 m2时,洞口外20 m 处微气压波峰值将由135.4 Pa降低到120.1 Pa,即由规范允许值的271%降低到240%,降低效果有限。同时,隧道断面面积增大必将引起线路建造成本及技术难度大幅的增加,因此,通过在洞口加设缓冲结构来降低微气压波峰值的方法更为适宜。
3.2 增设洞口缓冲结构
对于350 km/h的高速铁路隧道,主要洞口缓冲结构型式主要有喇叭型、等截面扩大、明洞斜切和洞周开孔等。考虑到400 km/h速度下高速隧道洞口微气压波值远超规范和350 km/h速度下的相应值,对各种缓冲结构及其组合方式的缓冲效果进行对比分析。以断面面积100 m2、长度 1 000 m 的隧道为例,分析缓冲结构及其组合方式下洞口微气压波峰值的缓冲效果,结果如表3所示。
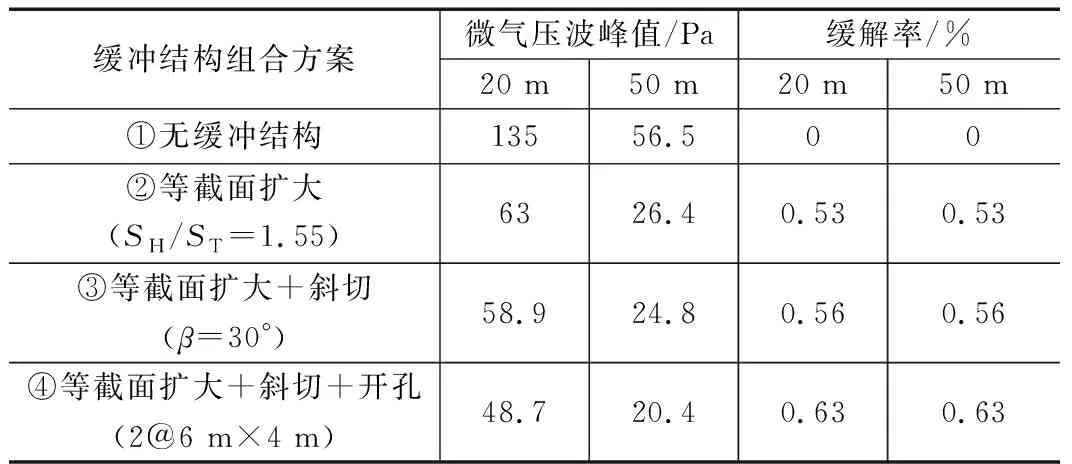
表3 不同洞口结构组合型式的缓冲效果对比表
从表3可以看出,对于400 km/h的高速铁路隧道, 采用单一的缓冲结构无法将洞口微气压波峰值降低到规范允许值以下,采用等截面扩大+斜切+开孔的组合型缓冲结构则可取得较好的降压效果。因此,建议400 km/h速度高速铁路隧道洞口采用等截面扩大+斜切+开孔的组合型缓冲结构。
3.3 缓冲结构形式及其设计参数分析
鉴于隧道洞口微气压波峰值与隧道长度存在一定相关性,以等截面扩大+斜切+开孔的组合型缓冲结构为基础,分析隧道长度400~6 000 m范围内缓冲结构的设计参数,结果如表4所示。
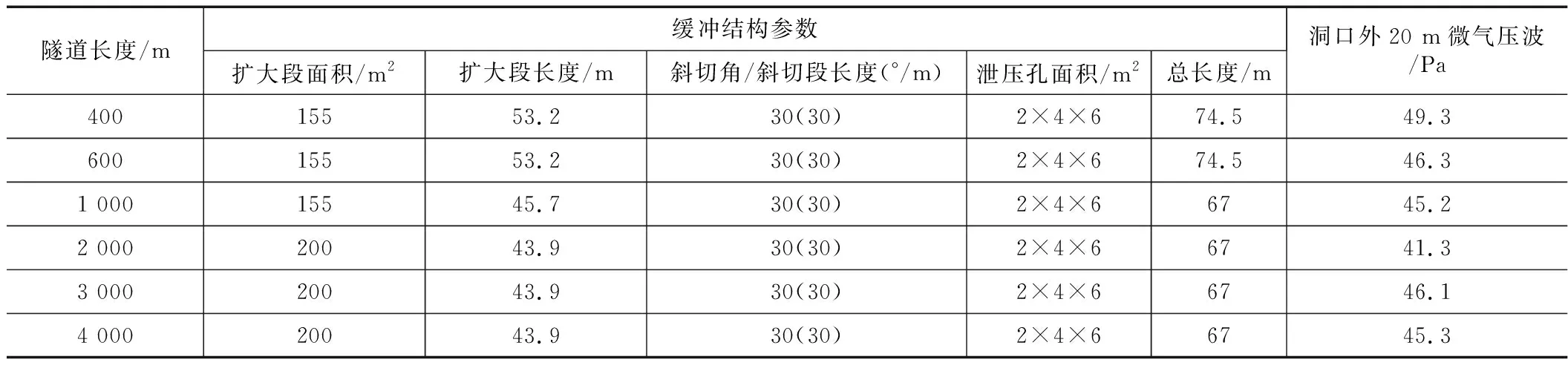
表4 不同隧道长度条件下洞口缓冲设计参数建议值表
4 结论及建议
本文采用室内动模型试验和数值计算相结合的方法,研究了400 km/h速度条件下高速铁路隧道洞口的微气压波特征,并基于国内外主要缓冲结构型式,对400 km/h速度条件下高速铁路隧道洞口的缓冲结构型式及其设计参数进行了量化分析,得到以下主要结论:
(1)隧道洞口微气压波峰值随列车速度的增大而急速增加,二者呈现超3次方(y=3x3.3)的正比关系, 400 km/h速度下隧道洞口微气压波峰值为 350 km/h速度下的1.61~1.74倍,且均远超规范要求。
(2)400 km/h速度下,洞口微气压波随隧道长度的增加而线性增加;350 km/h速度下,洞口微气压波随隧道长度的增加而线性降低。
(3)对于400 km/h的高速铁路隧道,单纯增大隧道断面或加设单一缓冲结构均不能满足现有规范要求,采用等截面扩大+斜切+开孔的组合型缓冲结构可将洞口微气压波降低到规范允许值以内。
(4)对于400 km/h的高速铁路隧道,隧道洞口微气压波峰值与隧道长度存在一定的相关性,应根据隧道长度对缓冲结构设计参数进行针对性优化分析。
本文主要是基于室内动模型试验和数值仿真两种研究方法进行的研究,最终实施效果应根据实测结果进一步验证。此外,对于更高速度下隧道洞口的结构型式及其微气压波特征,有必要结合空气动力学中等亚音速流的基础分析理论进行深入研究。

