降雨条件下不同黏粒含量土体的非饱和入渗特性

陈 亮， 司朋举， 张 赏

（1.河海大学岩土力学与堤坝工程教育部重点实验室，南京 210098； 2.河海大学土木与交通学院，南京 210098）

非饱和土体在自然界中大量存在，是饱和度大于0小于100的固、液、气三相混合体系，具有特殊的物理力学性质［1］，初始含水率较低，具有较高的基质吸力，稳定性好. 但是当遇到降雨天气时，雨水入渗非饱和土体后势必会引起土体含水率的增加，土壤基质吸力减小，从而引发相应的自然地质灾害，例如滑坡、泥石流等［2-3］. 大量工程实践经验表明，地基液化、边坡流滑等灾害现场土体中都含有一定含量的黏粒，黏粒对砂土液化等工程特性影响较大. 且在土壤学中，有些农作物在过砂或者过黏的土体中生长较差，一般采用客土的方法进行土壤改良，即砂掺黏. 据统计，我国现有耕地中，因耕层土壤质地过砂或者过黏而需要改良的土壤各在一亿亩以上［4］. 因此，研究降雨条件下不同黏粒含量土体非饱和入渗特性具有重要的现实意义.

前人对土体的入渗过程及其变化规律做了大量室内和室外的研究，也取得了颇为丰硕的研究成果. 王永义等［5］基于山西气象站的实测资料，从雨强、潜水面深度、岩性等方面分析和总结了降雨入渗补给规律. 朱伟和山村和也［6］使用降雨入渗试验来测量土壤水分和湿润锋的运动规律，并用有限元方法进行了饱和—不饱和入渗分析. 张士林［7］研究了强降雨条件下干土缓坡的入渗规律，并基于Green-Ampt入渗模型提出恒定雨强下的实际入渗关系式. 白盛元［8］在野外观测了10 m深的土柱的土壤水分动态变化，分析了自然降雨条件下土壤水分的入渗深度和补给量，水分入渗受到多种因素的影响，因而入渗过程持续时间不同. 陈洪松等［9］利用室内人工降雨试验，研究了初始土壤含水量对坡面降雨入渗的影响，结果表明，初始含水率越高，产流越快，再分布过程中湿润锋运移速率越大，且土体水分有沿坡向下运移趋势. 曾铃等［10］设计了一种可以测量土体吸力和含水量的降雨入渗装置，通过降雨试验研究了砂土和粉质黏土在不同雨强以及底部排水条件下含水率和吸力随时间的变化规律. 朱伟等［11］通过室内降雨入渗土柱试验，探究了降雨入渗的过程和入渗规律，并研究了能够准确反映降雨入渗量的有限元计算方法. 钟佩文等［12］在室内进行垂直一维降雨入渗过程，观察了土体内湿润锋和含水率的迁移规律，采用FLAC3D并结合实际参数模拟了该降雨过程，并分析了边坡的安全稳定性. 张世斌等［13］开发了一种可以测量土体电阻率和体积含水率的试验装置，并进行了降雨条件下重塑黄土水分迁移模型试验，研究结果表明，重塑黄土的水分迁移特征跟雨型有较大关系，小雨、大雨以及暴雨状态下入渗线分别呈现出“Y”型、“D”型以及“Λ”型的特点. 李达等［14］使用了土体瞬时渗透特性测试仪，对非饱和砂质紫色土进行了不同雨强条件下的一维垂直渗透试验，得到了砂质紫色土的非饱和渗透系数与雨强无关的结论. 包含等［15］利用TDR采集水分数据，通过室内人工降雨试验，从土壤含水率和湿润锋运移探讨了不同雨强对水分入渗以及土壤水分再分布情况. 孙媛等［16］采用了有限差分法，模拟了降雨及降雨停止后砂壤土水分运动的全过程，结果表明降雨强度对土壤水分再分布有较大影响，中层含水率变化较小，持水能力较强，有利于植物生长.

上述研究对非饱和土体入渗规律的分析具有重要的现实意义. 但是，目前大多数研究是考虑雨强、雨型、分层土及初始含水率等因素对降雨入渗规律的影响，而对于含有不同黏粒含量的非饱和土柱在降雨条件下的垂直入渗规律的研究相对较少. 本文自主设计加工了一套一维垂直土柱入渗模型试验装置，基于该试验装置研究了不同黏粒含量非饱和土柱的入渗规律，对保护和改良土壤、防止土壤侵蚀、防止水土流失、预防边坡失稳等工程问题具有十分重要的理论和实践意义.

1 试验装置及方案

1.1 试验装置的设计

降雨入渗试验仪器的主体部分为一维垂直土柱，采用厚度为5 mm厚的透明有机玻璃管制造，竖直一维土柱试验仪器高度为1 m，内径为14 cm，外径为15 cm，中间用一个法兰结构连接，便于土柱的安装和拆卸，土柱下端设置有排水口，便于排水.降雨入渗试验装置仪器结构示意图如图1 所示，图中结构示意图代表了整个降雨入渗过程试验装置的主要组成部分.

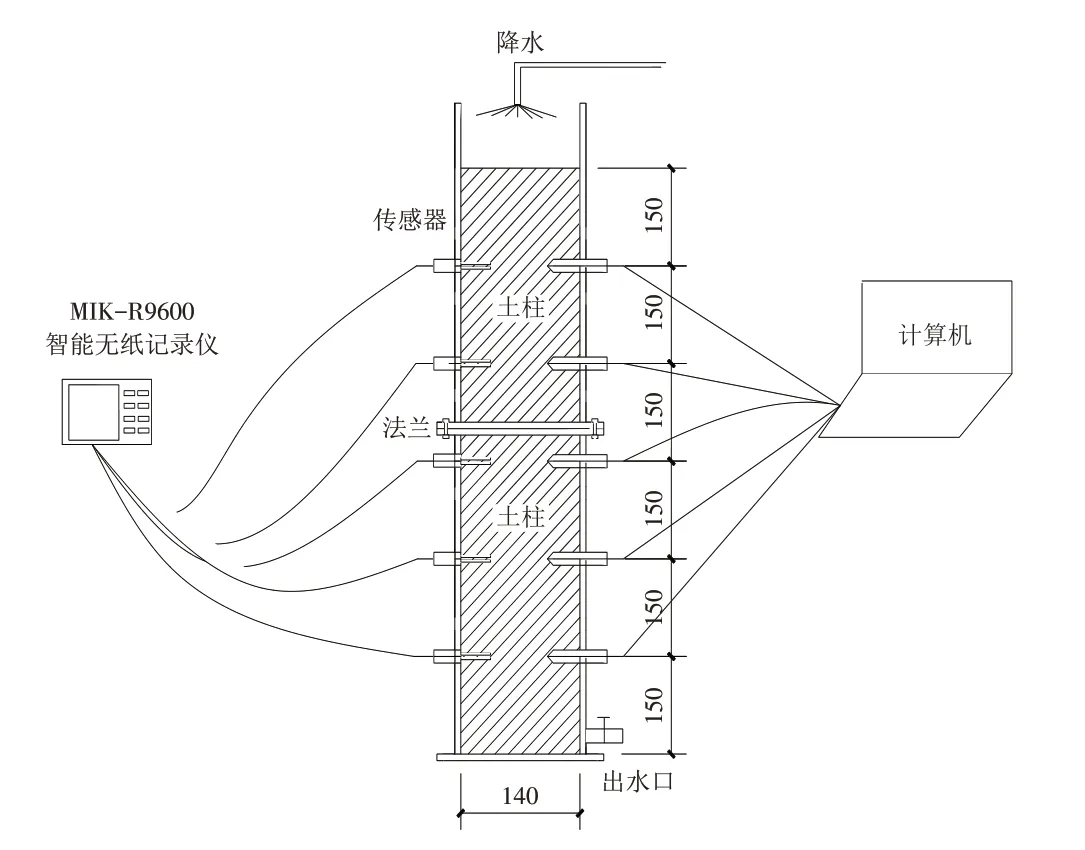
图1 降雨入渗室内试验仪器图（单位：mm）Fig.1 Indoor test instrument diagram of rainfall infiltration

一维垂直土柱上方有降雨装置，由降雨器和蠕动泵组成，蠕动泵可调节进入降雨器的水量，通过旋转开关调节每分钟的出水量，从而换算成相应的雨强，降雨器可以用来形成均匀降雨，二者联合共同构成降雨系统，如图2和图3所示. 土柱的左右两侧分别插入5个土壤水分传感器和5 个张力计，分别从土柱上端到底部依次编号为1#、2#、3#、4#、5#，用以监测土壤的体积水分含率和基质吸力. 每个水分传感器和张力计的间距为15 cm，填土高度为90 cm，以供积水存留. 在土柱侧边贴上刻度尺以供读取积水高度，从而可测得入渗量及入渗率的大小.

图2 蠕动泵Fig.2 Peristaltic pump

图3 降雨器Fig.3 Rainfall instrument

1.2 试验仪器

试验中使用EC-5土壤水分传感器来测量土体含水率［17-18］，土体是由固、液和空气组成的三相体系，土体介电常数受土体含水率影响很大. 该测试仪器使用Decagon公司开发的EC-5土壤水分传感器和配套数据记录设备来测量土壤体积含水率，如图4所示.

图4 EC-5土壤水分传感器Fig.4 EC-5 soil moisture sensor

试验所使用的张力计是一种新型的电子张力计［19-22］，目的是测量土壤的基质吸力，量程范围为0～100 kPa，该张力计的饱和程序简单，易操作，具有较高的灵敏度和可靠度，如图5所示.

图5 电子张力计Fig.5 Electronic tensiometer

1.3 EC-5土壤水分传感器标定

从EC-5土壤水分传感器的原理可知，对同一土体，传感器的输出信号值与被测土壤的体积含水率之间具有一一对应的映射关系. 因此，试验前需要对所用的5 支传感器分别编号为1#、2#、3#、4#、5#，然后配置7%、15%、23%、31%体积含水率的试样，将不同编号的土壤水分传感器分别插入到配置好的土样当中，测得土壤水分传感器所显示出的电压值，最后对不同编号的土壤水分传感器进行标定，得到含水率与输出信号电压值之间的关系. 5支传感器的输出信号值与体积含水率如图6所示.

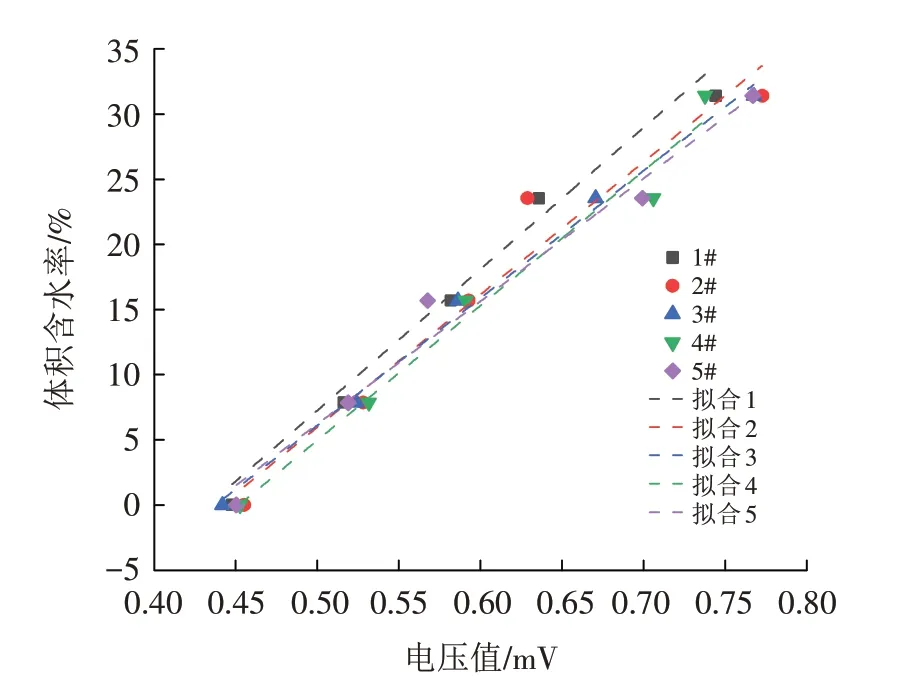
图6 土壤水分传感器标定曲线Fig.6 Calibration curve of soil moisture sensor

由图可知，1#、2#、3#、4#、5#传感器的输出信号值与体积含水率具有较好的线性关系，即随着含水率的增大，电压值也就越高. 通过线性拟合发现，R2基本都在0.95 以上. 通过拟合得到的电压与体积含水率关系曲线，可求出不同电压值所对应的体积含水率θW.

1.4 试验土样

为研究黏粒含量对非饱和土壤降雨入渗的影响，本试验选用砂土和高岭土作为研究对象. 为排除土体非均质性的影响，经过振筛机筛选粒径≤2 mm的砂样. 为减少土样中的杂质对试验结果的干扰，装样之前使用清水洗涤试样土，经过风干再进行试验. 试验砂样的级配曲线如图7所示，从图中级配曲线看出，粒径大于0.25 mm的颗粒超过全重的50%，根据《建筑地基基础设计规范》中砂土的分类标准可知，该试验土样为中砂. Cu=d60/d10=0.5/0.15=3.33＜5，颗粒均匀，为均匀中砂. 用此砂样为试验土样，土样孔隙均匀，不管细观上还是宏观上均可看作为均质土体. 黏土颗粒选用高岭土材料，将所需的黏粒掺配到砂土中，然后击实为干密度1.57 g/cm3的一维垂直土柱.

图7 颗粒级配累积曲线Fig.7 Cumulative curve of particle gradation

1.5 试验方案

试验为模拟不同黏粒质量分数下一维土柱垂直非饱和入渗特性，分别设置了黏粒质量分数为5%、10%、15%、20%、25%的5组模型试验，具体的试验方案如表1所示. 降雨强度为50 mm/h，土柱高度为100 cm，填土高度为90 cm，观测点分别设置在距离填土表面15、30、45、60、75 cm处.

表1 不同黏粒含量下降雨入渗试验方案Tab.1 Rainfall infiltration test schemes under different clay contents

2 实验结果及分析

2.1 不同黏粒质量分数下土柱的入渗率和累积入渗量分析

图8为不同黏粒含量一维垂直土柱入渗时的入渗率时程曲线，表2 为不同黏粒含量一维垂直土柱入渗时积水点和饱和点出现的时间.

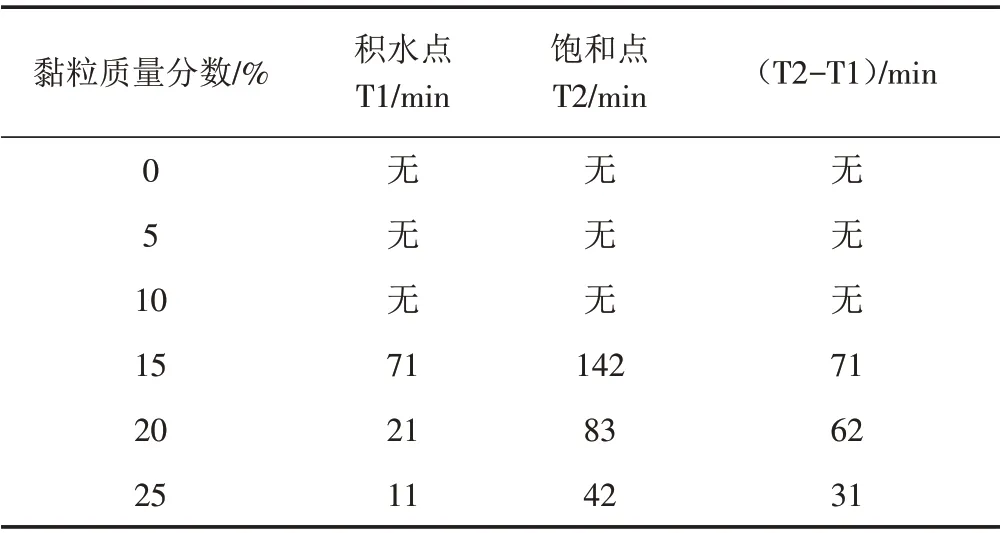
表2 积水点与饱和点出现时间Tab.2 Occurrence time of water accumulation point and saturation point

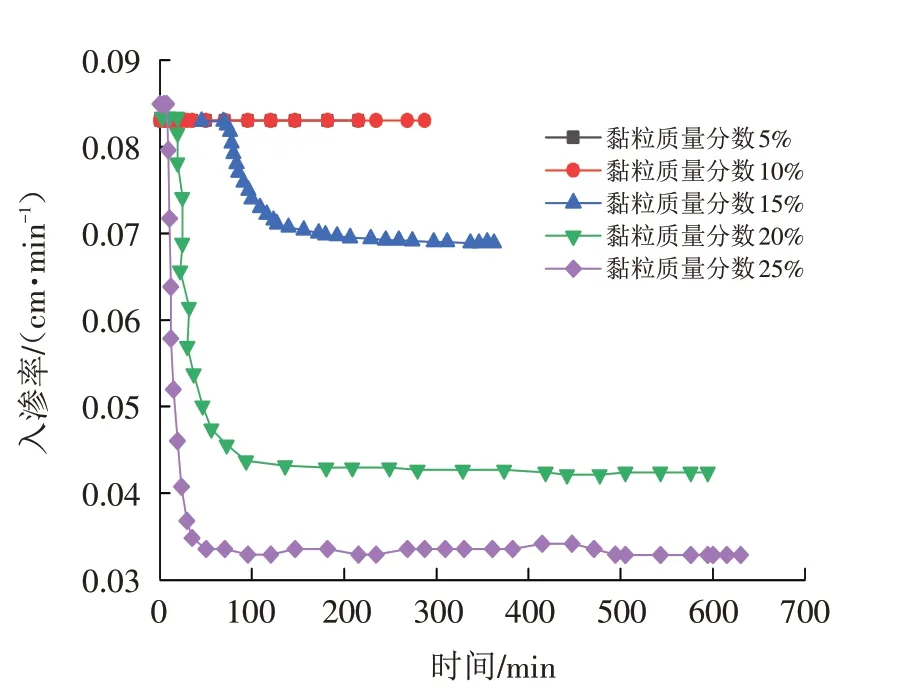
图8 同一雨强、不同黏粒质量分数下入渗率随时间变化关系Fig.8 The relationship of infiltration rate with time under the same rain intensity and different clay contents

分析可知，当降雨强度相同时，不同黏粒含量对土柱入渗率的影响具有如下特点：

1）由入渗率时程曲线可知，降雨强度相同时，对于不同黏粒含量的土体，其入渗率有较大差异. 当黏粒质量分数为5%和10%时，入渗率均为一条直线，且近似重合，土壤表面没有积水产生，说明当黏粒质量分数为5%和10%时，雨强均小于土壤最小入渗能力，入渗率为降雨强度等于0.083 cm/min.

2）当土体黏粒质量分数为15%、20%、25%时，此时的雨强超过土壤最小入渗能力，试验过程当中发现会有积水产生. 由图8和表2 可知，当黏粒质量分数为15%时，在前71 min 时间内，降雨水分入渗过程中无积水产生，此时土壤水分入渗率等于雨强，土体表面在71 min时刻出现积水，此时入渗率开始逐渐减小，在142 min 时刻，入渗率便减小到一稳定值，此后土体入渗率一直稳定保持不变；当黏粒质量分数为20%时，在前21 min 内，降雨入渗过程中无积水产生，此时入渗率等于雨强，土体表面在21 min时刻出现积水，此时入渗率逐渐减小，在83 min时刻，入渗率减小到一稳定值；当黏粒质量分数为25%时，在前11 min时间内，降雨入渗过程中无积水产生，此时入渗率等于雨强，土体表面在第11 min 时刻出现积水，此时入渗率开始逐渐减小，在42 min时刻之后，入渗率便减小至一稳定值.

3）根据之前所述，有积水的降雨入渗过程分为3 个阶段，由图8 和表2 可知，当土体黏粒质量分数处于15%～25%范围时，在第一阶段，黏粒质量分数越高，同一雨强下处于第一阶段的时间也就越短，积水点依次从71 min减为21 min再减为11 min，且此时土壤水分入渗率均为定值且相同，均等于降雨强度0.083 cm/min.在第二阶段非饱和入渗阶段，随着黏粒质量分数增加，入渗率减小的速度也就越快，当黏粒质量分数为15%、20%、25%时，土壤水分入渗率减小至稳定含水率的时间间隔依次为71、62、31 min. 在第三阶段，随着黏粒质量分数依次增加，饱和点出现时间依次减小，且稳定入渗率的值随着黏粒质量分数增大而减小. 这是由于随着黏粒含量增加，黏粒填充了较大土体颗粒之间的孔隙，导致土体颗粒之间孔隙减小，土体渗透性变差，土壤饱和渗透系数越来越低，而稳定入渗率为饱和入渗阶段，所以随着黏粒含量增大，其稳定入渗率越来越低.

图9为同一降雨强度下不同黏粒含量土柱的累积入渗量与时间的变化关系曲线，由图可知：

1）当土体黏粒质量分数分别为5%和10%时，雨强小于土壤的最小入渗能力，降雨过程中所有水分均渗入到土体内部，累积入渗量为一条过原点的直线，直线的斜率为降雨强度，二者累积入渗量曲线近似重合，但是两者达到土柱底端的累积入渗量不一样. 当黏粒质量分数为5%时，水分入渗到土柱底端所需要的时间为202 min. 当黏粒质量分数为10%时，水分入渗到土柱底端所需要的时间为284 min. 即随着黏粒质量分数增加，虽然此时无积水产生，但是水分运移的速度会减慢，水分到达土柱底端所需时间会变长，相应的水分运移到土柱底端时，累积入渗量也会增大.

2）当土体黏粒质量分数为15%、20%、25%时，此时的雨强大于土柱的最小入渗能力，累积入渗量变成了一条上凸的曲线，而不再是一条直线. 这表明随着黏粒质量分数的增加，水分入渗速率增速逐渐减慢. 由图9 可知，在50 min 时刻内，五组不同黏粒质量分数的累积入渗量曲线接近重合，说明在前50 min 之内，其入渗速率接近一致，而在50 min 之后不同黏粒质量分数土体的累积入渗量差距逐渐增大，在同一时刻下，随着黏粒质量分数增加，相应的累积入渗量逐渐降低，但降低的幅度存在差异. 当黏粒质量分数为5%、10%、15%时，相同的时间内累积入渗量降低的幅度比较小；但随着黏粒质量分数继续增加，当黏粒质量分数为20%、25%时，累积入渗量减小幅度较大，其中黏粒质量分数在15%～20%之间时，土体累积入渗量减小幅度最大.

图9 不同黏粒含量土柱的累积入渗量与时间的变化关系Fig.9 Relationship between cumulative infiltration volume of soil columns with different clay contents and time

图10为土体黏粒质量分数与累积入渗量之间的关系图，由图可知，当降雨入渗到土柱底端时，总累积入渗量随着黏粒质量分数的增大而增大，但其增长幅度并不一致，当黏粒质量分数为15%以下时，累积入渗量随着黏粒质量分数的增加而大幅提高，而当黏粒质量分数在15%以上时，累积入渗量随着黏粒质量分数的增加变化不大，原因在于当黏粒质量分数小于15%时，在降雨入渗的过程中并无积水出现，整个土柱的入渗均为非饱和入渗状态，此时土壤的峰值体积含水率比较低，因此累积入渗量较小，且随着黏粒质量分数的增大而增大. 而当黏粒质量分数大于15%时，降雨入渗过程中出现了积水入渗，土壤的峰值体积含水率接近于土壤饱和含水率，而在黏粒质量分数为15%以上时土壤饱和含水率随着黏粒质量分数的增加增幅不是很大，因此总的累积入渗量并不会随着黏粒质量分数而有大幅度提高.

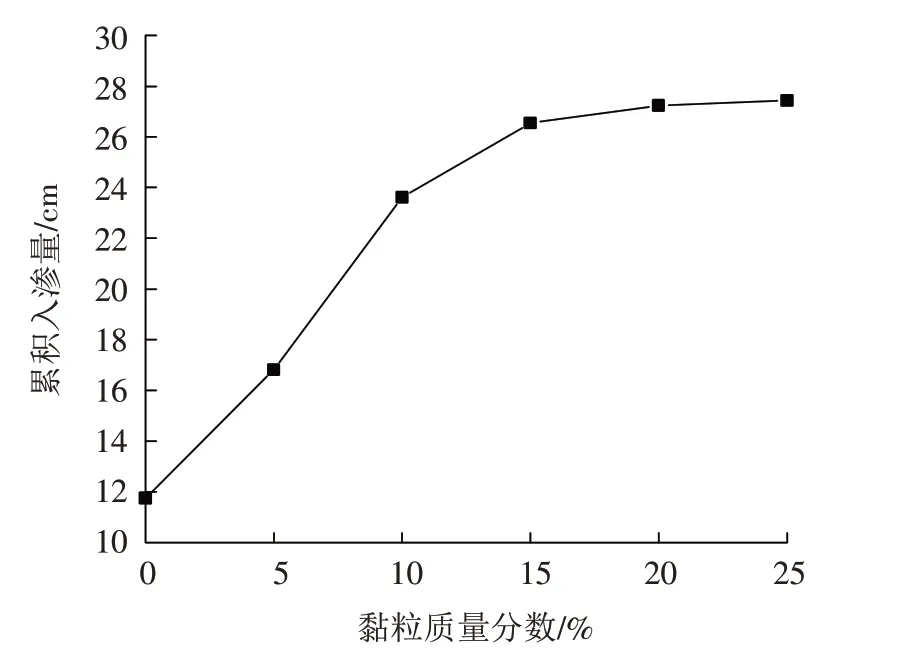
图10 黏粒质量分数与累积入渗量之间的关系Fig.10 The relationship between clay mass fraction and cumulative infiltration volume

2.2 监测点的土壤体积含水率分析

由图11同一降雨强度下的监测点的含水率时程曲线可知，不同黏粒质量分数下的峰值含水率存在差异，当黏粒质量分数分别为0%、5%、10%、15%、20%、25%时，土体的峰值含水率分别为20%、28%、35%、37%、38%、40%，由此可知土体的峰值稳定体积含水率随黏粒质量分数的增加而逐渐增大. 由图12可知，土体黏粒质量分数以10%为分界点，当黏粒质量分数在10%以下时，此时土体峰值体积含水率较低；随着黏粒质量分数增加，峰值体积含水率增量较大；当黏粒质量分数位于10%以上时，峰值体积含水率也随着黏粒质量分数的增加而增加，但其增量较小.

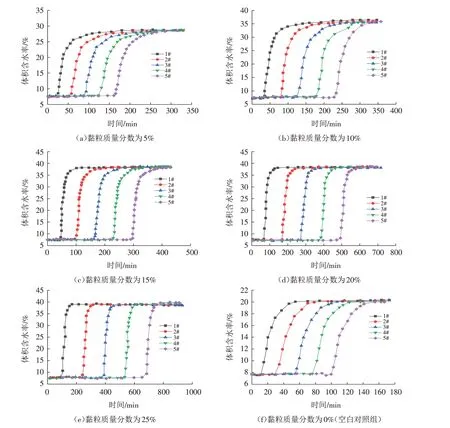
图11 50 mm/h雨强及不同黏粒质量分数下监测点体积含水率随时间的变化关系Fig.11 The relationship between the volumetric water content of monitoring points and time under the conditions of 50 mm/h rain intensity and different clay contents

图12 黏粒质量分数与峰值体积含水率的关系Fig.12 The relationship between the mass fraction of clay particles and the peak volumetric water content

不同黏粒质量分数沙土在相同雨强条件下，湿润锋深度随时间的变化关系趋势如图13所示，在相同降雨条件下，黏粒含量越高，在同一时刻，湿润锋运移的距离也就越短，以黏粒质量分数15%为分界点，当黏粒质量分数小于15%时，湿润锋深度随时间的变化增幅较小；而当黏粒质量分数大于15%时，湿润锋深度随时间变化幅度相对较大.

图13 湿润锋随时间的变化关系Fig.13 The relationship between wetting front and time

图14给出了降雨入渗到土柱底端时，水分入渗到土柱底端所需时间与黏粒质量分数之间的关系，由图可知，随着黏粒含量增加，水分入渗土柱底端的时间相对就越长，以黏粒质量分数15%为分界点，当黏粒质量分数小于15%时，水分入渗到土柱底端的时间增幅较小，而当黏粒质量分数大于15%时（即20%、25%），此时水分入渗到土柱底端所需的时间增幅较大.

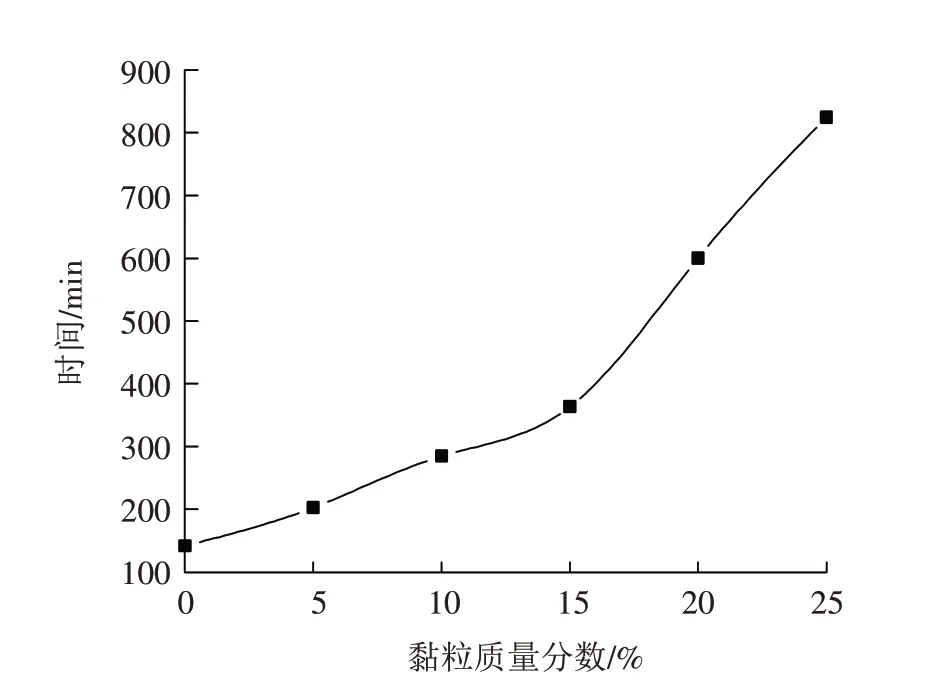
图14 水分运移到土柱底端时间与黏粒质量分数之间的关系Fig.14 The relationship between the time of water migration to the bottom of the soil column and the content of clay particles

2.3 不同黏粒质量分数下土壤水分特征曲线分析

通过与所测得的土壤水分体积含水率和土壤基质吸力进行对应，便得到了土壤体积含水率与基质吸力的关系，将体积含水量与其对应的基质吸力绘制到一张图，便可得不同黏粒含量下砂土的土水特征曲线.

由图15可知，土壤体积含水率与基质吸力整体呈现出负相关关系，土壤体积含水率随着基质吸力增加而逐渐减小，且随着土壤黏粒质量分数增加，体积含水率降低的速率也就越迟缓. 当土壤基质吸力较小时，其土水特征曲线近似重合，说明此时黏粒质量分数对基质吸力影响较小. 而随着基质吸力增大，其土水特征曲线差异性明显增大，当基质吸力为80 kPa 时，10%、15%、20%、25%黏粒质量分数对应的体积含水率分别为7%、10%、13%、16%，说明体积含水率随着黏粒含量增加而逐渐增大，这也表明提高土壤黏粒含量可以增大土壤基质吸力.

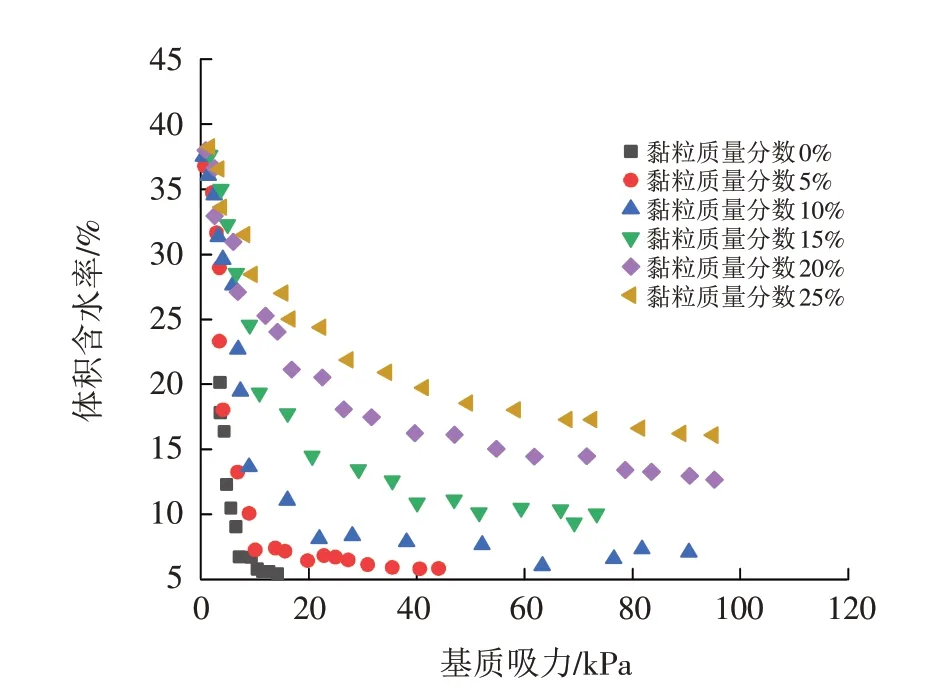
图15 不同黏粒质量分数下的土水特征曲线Fig.15 Soil-water characteristic curves under different clay contents

为得到不同黏粒含量下沙土体积含水率与基质吸力之间的关系，采用VG模型进行拟合，土体残余含水率为7%，饱和含水率按照试验设计容重1.57 g/cm3，将试验用的砂土和黏粒质量分数烘干，利用环刀法测量土体饱和含水量. 结果在容重1.57 g/cm3下，黏粒质量分数分别为0%、5%、10%、15%、20%、25%的饱和含水率θs为36.3%、37.0%、37.5%、37.9%、38.4%、38.9%.

由图16可知，土壤的饱和含水率与黏粒质量分数呈正相关关系，黏粒含量越大，饱和含水率也就越大，即土壤的持水能力随着黏粒含量的增大而增大，通过进行线性拟合，得到拟合公式：

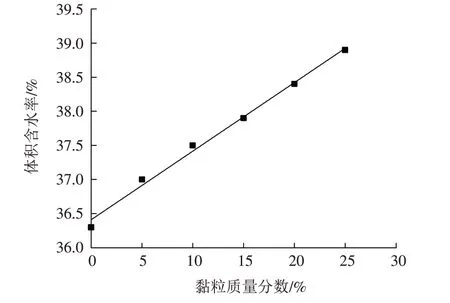
图16 不同黏粒质量分数下的饱和含水率Fig.16 Saturated water content under different clay contents

其中：y为土壤饱和体积含水率；x为土壤黏粒质量分数.

采用VG模型［1］（见公式（2））对不同黏粒含量下的土水特征曲线进行拟合，VG模型里面共有4个参数，已知θr，θs前面已经给出，因此拟合未知量为α.

其中：θs为饱和含水量；θr为残余含水量；α是与进气吸力相关的参数；φ是基质吸力；n和m是形状系数，并且m=1-1/n.

利用公式（2），对所得到的实验数据进行拟合分析，曲线拟合所得的α值、n值、m值结果如表3所示.

表3 不同黏粒质量分数下土壤水分特征参数拟合值Tab.3 Fitting values of soil moisture characteristic parameters under different clay contents

在VG模型当中，土壤水分特征曲线的拟合参数有m、n、α，其中m是与曲线斜率有关的参数，n是与土体孔隙均匀性有关的参数，α是与土体进气状态有关的参数. 由表5可知，α值、n值、m值均随着黏粒质量分数的增大而减小. 这是由于当砂土含有黏粒时，随着黏粒含量增大，以及随着土壤吸力增加时，含水量的减少较为缓慢，因此曲线的斜率坡度越来越缓和. 通过对α进行线性拟合，对n进行二次函数拟合，结果如下：α=-0.005 61CC+0.32，R2=0.96；n=4.947-0.313CC+0.007CC2，R2=0.99，其中CC代表黏粒质量分数.

由此可以得到不同黏粒质量分数条件下的土水特征曲线公式，知道砂土中黏粒质量分数即可以得到其体积含水率与基质吸力之间的关系：

3 结论

降雨入渗过程是土壤水循环的重要过程，也是土质边坡诱发滑坡、泥石流等自然灾害的重要因素. 本实验通过自行设计加工的试验装置对初始体积含水率为7%，土体容重为1.57 g/cm3的一维垂直土柱进行了5组不同黏粒质量分数下的入渗试验研究，得到了如下主要结论：

1）黏粒质量分数对垂直土柱的入渗影响较大，当黏粒质量分数小于10%时，降雨强度小于土体的最小入渗能力，垂直土柱的入渗率时程曲线为一平行于横轴的直线，入渗率等于降雨强度且恒等于0.083 cm/min；当黏粒质量分数大于15%时，降雨强度大于土体的最小入渗能力，垂直土柱的入渗率时程曲线呈现无压入渗、有压入渗和饱和入渗三阶段变化.

2）从不同黏粒含量下积水点和饱和点的时间节点可知，积水点和饱和点随着黏粒含量的增大而减小.

3）累积入渗量和土壤稳定含水率分别以黏粒质量分数15%和10%为拐点，两侧增幅并不一致，左边增幅较大，右边增幅较小.

4）从监测点体积含水率的分布可知，垂直土柱上表面的体积含水率并不是迅速达到饱和，而是经过由非饱和到暂态饱和再到饱和的一个过程，体积含水率随着黏粒含量的增加而线性增加.

5）研究中运用VG模型拟合分析了不同黏粒质量分数下的土水特征曲线，结果显示黏粒质量分数越高，α值、n值和m值都减小，α值与黏粒质量分数是线性关系，n值与黏粒质量分数是二次函数关系.