矩形竹片剖分模型在竹筒开片中的应用1)

刘嘉诚 谢力生 李婷 陶钧

(中南林业科技大学，长沙，410004) (湖南桃花江竹材科技股份有限公司) (中南林业科技大学)

我国竹材资源十分丰富[1-2]，而工业用木材资源非常匮乏[3-4]，用竹材替代木材生产需求日益增长的家居(具)和建筑材料，具有十分重要的意义[5-7]。竹集成材，是将规格竹片顺纤维方向加宽、加厚组坯胶合而成的一种板材或方材[8-10]，广泛应用于地板和家具制造，其中结构用竹集成材还可用作建筑结构的梁或柱使用[11-13]。普通竹集成材的生产已经超过20 a，生产工艺成熟，产量也不断提高。但由于竹筒的开片数及竹片的截面尺寸规格主要由经验决定，出材率始终难以提高，直接影响企业的经济效益。

关于竹筒剖分(开片)的研究很少，2008年王彦斌等[14]对竹筒的剖分进行了研究，将竹筒看作有一定厚度的圆壁筒，建立竹筒内、外径和竹片截面尺寸与开片数三者之间的数学模型，推导出了相应优化剖竹(开片)的计算公式。该研究没有考虑竹片的加工余量，与生产实际存在差距。为此，2012年郝景新等[15]考虑竹片加工余量，重建了竹片剖分的数学模型，研究表明：开片数、加工余量、竹筒直径，对矩形竹片出材率影响显著；加工余量越大，最优(即材料利用率最大)开片数值越小；竹筒直径越大，最优开片数值越大；竹筒直径小于80 mm时，竹材利用率偏低，已不再适合加工成矩形竹片。

前述两次研究，均将竹片的矩形截面形状认定为如图1的(1)所示，且没有研究竹筒直径与壁厚的关系，不能直接由竹筒直径决定合理的开片数。由图1的(2)所示，竹片形状尺寸可知，与(1)相比竹片厚度更大，且更符合实际情况。为此，笔者按图1的(2)的竹片形状开展竹筒剖分(开片)研究，同时研究竹筒直径与竹壁厚度的关系，力求能通过竹筒小头直径，针对规格竹片提出竹筒的最佳开片数，提高竹材利用率。旨在为生产实际提供参考。

图1 矩形竹片制备示意图

1 材料与方法

毛竹(Phyllostachysheterocycle)：产自湖南桃江，竹龄3～4 a，胸高1 m处直径55～115 mm，主干高4～7 m，总计25根。用于求取毛竹直径与壁厚的数学模型。

将毛竹从头至尾截成1 m长的竹筒，共计得到竹筒152根。用数显游标卡尺测量每根竹筒的小头长径、短径及其壁厚，数值精确至0.01 mm，取两者的平均值作为竹筒小头的直径、壁厚。根据152个直径和壁厚值，求取毛竹直径与壁厚的数学模型。

为简化计算，假设竹筒为圆形截面，竹筒剖分及竹片截面几何分析见图2。设竹筒直径为D、壁厚为B、剖分(开片)数为n，矩形(规格)竹片宽度为h、厚度为b及理论截面积为A0，由图2可知：

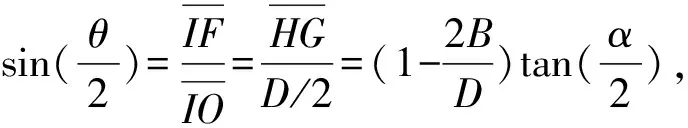
在△EIO中，

设竹片的加工余量为(δ)，则竹片最终截面积A=(b-δ)(h-δ)；在不考虑竹筒尖削度时，竹筒的出材率(等于截面出材率)η=4n(b-δ)(h-δ)/π[D2-(D-2B)]。

图2 竹筒剖分及竹片截面几何示意图

由于矩形(规格)竹片不允许钝棱存在，其截面尺寸(宽度、厚度)和开片数由竹筒的小头直径决定，且考虑尖削度的竹筒的出材率与竹筒截面出材率正相关，即竹筒截面出材率增大或减小，一定长度的带尖削度的竹筒的整体出材率也增大或减小，为此，本研究只讨论竹筒小头截面出材率，并将其作为竹筒截面出材率来间接说明竹筒的整体出材率。

2 结果与分析

2.1 竹筒直径与壁厚的关系

由152根竹筒测得直径、壁厚的平均值(见图3)，毛竹壁厚(B)可由其直径(D)按公式B=0.082 1D+1.594 8计算获得。毛竹直径与其壁厚具有很好的线性正相关(R2=0.870 9)，即竹筒壁厚随其直径的增大而呈线性增大。

2.2 竹筒直径、开片数和加工余量与竹片截面尺寸及出材率的关系

由竹筒小头直径(D)、开片数(n)、加工余量(δ)计算出的矩形竹片的理论截面尺寸(宽度h、厚度b)及截面出材率(η)，表1为部分数据。

图3 竹筒直径与壁厚的关系

表1 竹筒直径、开片数和加工余量与竹片截面尺寸及截面出材率

nD=80mm,B=8.16mmb/mmh/mmη1/%η2/%η3/%η4/%D=60mm,B=6.52mmb/mmh/mmη2/%η4/%75.1030.6746.2833.8322.1311.194.3122.6130.403.6685.9226.3854.2741.5429.6918.694.9019.4536.9610.1596.4423.1859.0146.0033.9622.915.2817.0940.6313.74106.8020.6962.0048.7136.4925.375.5315.2642.7715.76117.0518.7063.9850.3937.9926.795.7213.7944.0016.88127.2417.0665.3151.4338.8527.575.8512.5844.6717.42137.3815.7066.2152.0439.2827.935.9611.5744.9617.59147.4914.5366.8252.3539.4127.986.0410.7244.9917.49157.5813.5467.2252.4639.3327.836.109.9844.8317.22167.6612.6767.4652.4139.1027.526.159.3444.5416.80177.7111.9067.5852.2438.7527.106.208.7844.1516.29187.7611.2367.6251.9938.3126.596.238.2843.6815.70197.8110.6367.5951.6737.8126.026.267.8443.1515.06207.8410.0967.5051.2937.2525.386.297.4442.5814.36217.879.6067.3750.8736.6524.716.317.0841.9613.63227.909.1667.2050.4136.0124.006.336.7541.3212.87237.928.7567.0049.9235.3523.276.356.4540.6512.09247.948.3866.7849.4134.6622.516.366.1839.9511.29

2.2.1竹筒开片数与竹片截面尺寸、理论截面积的关系

由表1可见：竹片厚度(b)随竹筒开片数(n)的增加而增大，开片数较小时增大明显，开片数较大时增大变得平缓；竹片宽度(h)随竹筒开片数(n)的增加而减小，开片数较小时减小很明显，开片数较大时减小的幅度变小。根据表1中的竹片厚度(b)、宽度(h)，可以计算出竹片的理论截面积(A0)。由图4可见：随着开片数的增加，竹片理论截面积(A0)先增后减，竹筒直径越大其增减越明显，开片数(n)为7(竹筒直径D<90 mm)或8(D≥90 mm)时竹片理论截面积(A0)有最大值；开片数(n)较大时，竹片理论截面积(A0)的减小变得缓慢。

图4 竹片理论截面积与竹筒开片数的关系

2.2.2 竹筒开片数与截面出材率的关系

由表1可见：考虑加工余量时，竹筒的截面出材率(η)在某一开片数(n)时有最大值(黑体数字)，该n值随竹筒直径(D)的增大和加工余量(δ)的减小而增大。例如，加工余量(δ)取2 mm，直径(D)为120、100、80、60 mm的竹筒，在开片数(n)分别为17、16、15、14时，有最大截面出材率61.60%、57.69%、52.46%、44.99%。若开片数(n)均取15，则直径(D)为120、100、80、60 mm的竹筒，对应的截面出材率分别为61.26%、57.58%、52.46%、44.83%，比最大截面出材率分别仅减少了0.55%、0.19%、0、0.36%。说明开片数(n)在14～17范围内，其取值对最大截面出材率的影响很小。

以竹筒直径(D)取100 mm为例，加工余量(δ)取1、2、3、4 mm，竹筒在开片数(n)分别为20、16、15、14时有最大截面出材率，分别为70.93%、57.69%、46.15%、35.82%。若开片数(n)均取15，则加工余量(δ)为1、2、3、4 mm时，对应的竹筒截面出材率分别为70.09%、57.58%、46.15%、35.81%，比最大截面出材率仅减少了1.18%、0.19%、0、0.03%。说明开片数(n)在14～20范围内，其取值对最大截面出材率的影响甚微。可见，无论从竹筒直径(D)，还是加工余量(δ)进行考量，竹筒开片数(n)在14～20范围内，其取值对最大截面出材率的影响均很小；为了减少开片刀轮和换刀，获取最大截面出材率的竹筒开片数(n)，统一取15是合理的。

2.2.3 竹筒开片数的取值范围

开片数为7或8时可获得理论截面积(A0)最大的矩形竹片，而开片数为15时可获得最大截面出材率。这说明开片数(n)在8～15的范围内都是可行的，开片数较小时可得到较大截面积的竹片而截面出材率较低，开片数较大时可得到较高的截面出材率而竹片截面积偏小。例如，比较表1中η2的数值可知，n由15减至8时截面出材率下降了1/4～1/5，但单个竹片的截面积增加了一半左右，这说明生产相同截面积的竹集成材或竹层板，其竹片数量可以减少一半左右，竹片的加工数量和组坯工作量均将减少一半左右，生产效率大为提高。因此，适当减少开片数更为有利。

为了不致使竹筒截面出材率太低，建议采用折衷处理，取开片数(n)为12。此时，与开片数为15相比，截面出材率下降不到3.80%，而单个竹片的截面积增加了约20%，则生产相同截面积的竹集成材或竹层板，其竹片数量相应减少约20%，竹片的加工数量和组坯工作量均可减少约20%。因此，开片数取12是较为理想的。此时竹片的具体加工尺寸可参照表1，按竹筒小头直径(D)和加工余量(δ)确定；或根据前述公式进行计算获取。

2.3 依据规格竹片的竹筒开片数的确定

2.3.1 依据宽度的规格竹片

结构用竹集成材，一般使用侧压型竹层板。对于侧压型竹层板，其厚度即为竹片的宽度，因此要求竹片的宽度一致。侧压型竹层板一般采用双向平板热压机压制，从热压传热效率角度考虑，竹层板的厚度(即竹片的宽度(h))一般不应超过25 mm；另外，为了使竹片具有较大的刚度，其厚度(b)不应小于3 mm。目前，规格竹片还没有制定标准，企业常用宽度尺寸多为22 mm左右，厚度尺寸一般在4.5～6.5 mm范围。因此，本研究将规格竹片宽度(h)定为22 mm进行分析讨论，厚度(b)按0.5 mm进级。由计算数据(见表1)，可找出满足竹片宽度(h)的不同直径(D)的竹筒的最佳(竹片厚度大，且竹片数多、截面出材率大)开片数(n)及规格竹片的厚度(b)尺寸(见表2)。

由表2可见：①生产等宽的规格竹片时，竹筒直径(D)越大，最佳开片数(n)越大，竹筒截面出材率(η)也相对越高，且竹片厚度(b)也越大；而竹筒直径(D)越小，最佳开片数(n)越小，竹筒截面出材率(η)也相对越低，且竹片厚度(b)也越小，当竹筒直径小于80 mm时已不能生产出宽度(h)为22 mm的规格竹片。为此，在表2中，竹筒直径(D)较小部分补充了宽度(h)为18 mm的数据，可以看出，当竹筒直径小于80 mm时，同样难以生产满足宽度(h)为18 mm的规格竹片。因此，直径小于80 mm的竹筒不再适合生产依据宽度的规格竹片，该结果与郝景新等[15]的研究结果一致。②竹筒直径(D)对应着相应的最佳开片数(n)，对于常见宽度22 mm的规格竹片，竹筒小头直径(D)为120、110、100、90 mm时，对应的最佳开片数(n)分别为12、11、10、9。其它宽度的规格竹片，可以参照表2进行填补、查找。③加工余量(δ)直接影响竹片的厚度(b)，加工余量每增加1 mm，竹片厚度相应减小1 mm，因此，应尽量提高加工精度、减小加工余量。

表2 不同直径竹筒的最佳开片数及规格竹片厚度尺寸

2.3.2 依据厚度的规格竹片

用于制造地板和家具等的普通竹集成材，一般使用平压型竹层板。对于平压型竹层板，竹单板的厚度即为竹片的厚度，因此要求竹片的厚度一致。将规格竹片厚度(b)按0.5 mm进级，宽度(h)按2 mm进级，开片数取8～15，根据计算数据(部分数据见表1)可找出不同直径(D)竹筒的合理开片数(n)及规格竹片的厚度(b)和宽度(h)的尺寸(见表3)。

表3 不同直径竹筒的开片数及规格竹片宽度尺寸

续(表3)

由表3可见：竹筒直径(D)越大，可生产的规格竹片的厚度(b)和宽度(h)越大，可生产的竹片规格(b×h)也越多；开片数(n)在8～15范围内，取值越大，规格竹片的厚度越大，而宽度越小，单竹片的截面积也越小，但截面出材率越大。相反，竹筒直径越小，可生产的规格竹片的厚度和宽度越小，可生产的竹片规格也越少。当竹筒直径(D)小于80 mm时，已基本上不能生产厚度为5 mm的规格竹片，且竹片的宽度也较小，只能勉强生产厚度3 mm或4 mm的个别小截面规格竹片。考虑生产成本等因素，不建议使用小头直径小于80 mm的竹筒生产规格竹片。依据厚度(b)的规格竹片的竹筒开片数(n)，具体可根据竹筒小头直径(D)、加工余量(δ)和需要的竹片规格(b×h)，参照表3进行选取。因此，表3可视为依据厚度的规格竹片的检索表。

3 结论

毛竹壁厚随其直径的增大而呈线性增大。

竹筒开片数增加，竹片厚度增大而宽度减小，开片数较小时变化较明显，开片数较大时变化很小；开片数取8时，可获得最大截面的矩形竹片。

考虑竹片加工余量时，竹筒的截面出材率随开片数的增加先增后减，开片数取15时可获得最大截面出材率。

竹筒开片数的合理取值范围为8～15。综合考虑各因素，开片数取12较为理想。

对于宽度22 mm的规格竹片，竹筒小头直径为120、110、100、90 mm时，对应的最佳开片数(n)分别为12、11、10、9。

小头直径小于80 mm的竹筒不适合用来生产规格竹片。