碳中和背景下长三角城市绿色全要素生产率再核算

何宇

摘要：基于碳中和背景，借助Malmquist-Luenberger生产率核算方法，使用净碳排放替换碳排放指标，构建碳中和背景下长三角城市绿色全要素生产率核算框架。使用2000—2017年长三角地区26个城市的碳排放和碳捕集数据进行测度，研究发现：调整后的绿色全要素生产率指数能够更科学、准确地反映地区绿色发展效率;长三角地区城市之间的绿色发展效率存在正向的空间关联，绿色发展效率高的城市对邻近城市具有正的溢出效应;长三角地区城市绿色发展效率存在显著的“多核共进”的协同发展特征，省会城市在长三角内部的绿色发展方面发挥了区域性的协同作用。进一步推动长三角地区绿色协同一体化，应建立健全碳排放、碳捕集数据的统计核算体系，优化区域经济空间布局，统筹促进经济发展、保护生态环境与应对气候变化的关系，提升长三角地区的生态韧性与发展韧性。

关键词：碳中和;碳捕集;长三角城市群;绿色全要素生产率;长三角一体化发展;生态韧性

中图分类号：F127  文献标识码：A  文章分类号：1674 .7089（2021）05 .0051 .10

一、引 言

2020年9月，习近平主席在第75届联合国大会一般性辩论中向全世界庄严宣布，中国将力争于2030年前实现碳达峰，在2060年前实现碳中和。2021年3月，习近平总书记发表重要讲话并强调，要把碳达峰、碳中和纳入生态文明建设整体布局，拿出抓铁有痕的劲头，如期实现2030年前碳达峰、2060年前碳中和的目标。碳达峰和碳中和承诺体现了中国作为世界第二大经济体的责任和担当，也对未来中国城市推进低碳、零碳高质量发展指出了政策方向。长三角是中国经济发展最活跃、开放程度最高、创新能力最强的区域之一，在推进低碳、零碳高质量发展方面具有重要示范作用。郑明贵、曾健林、曹天琦：《能源消费结构升级与区域经济高质量发展——基于产业结构的中介作用和人口红利的调节作用》，《阅江学刊》，2021年第3期，第85-101页。在碳达峰和碳中和政策背景下，恰当地对长三角地区城市绿色发展效率进行测度，对于科学准确研究长三角地区绿色协同发展，探索低碳、零碳背景下的绿色一体化政策路径具有重要意义。

近年来，气候变化问题受到学界广泛关注。Root等研究发现，在过去的100年内，全球平均气温上升了0.6℃，并且在很大程度上是人类工业碳排放导致的。 Root T L， Price J T， Hall K R， “Fingerprints of global warming on wild animals and plants”，Nature， vol. 421， no.3（2003）， pp.57-60.气候变化、环境污染等不仅破坏自然生态，也危及人类健康和生存空间。黄栋、王文倩：《气候共同体：后巴黎时代应对气候变化的东盟方式》，《阅江学刊》，2021年第1期，第46-59页。从经济学视角来分析，气候和环境问题会对区域经济发展造成不利影响，任力：《气候变化与经济增长的理论分析》，《经济学动态》，2011年第1期，第137-142页。主要体现在抑制工业产出、抑制投资和减少农业产出三个方面。Dell M L， Jones B， Olken B A， “Temperature shocks and economic growth： Evidence from the last half century”，American Economic Journal： Macroeconomics， vol. 4， no.3（2012）， pp.66-95.

当前，全球范围内大多数国家开始施行环境保护政策，如何兼顾经济产出效率和生态环境保护成为研究焦点。产出效率核算的基本理论分析框架起源于Chung等的开创性研究。Chung Y H， Fare R， “Productivity and undesirable outputs： A directional distance function approach”，Journal of Environmental Management， vol.51，no.3 （1997）， pp.229-240.在传统的基于索洛余值的全要素生产率核算（以下简称TFP）模型中，投入要素包括资本投入和劳动投入，产出则由经济实际总产出表示。王永进、刘灿雷：《国有企业上游垄断阻碍了中国的经济增长？——基于制造业数据的微观考察》，《管理世界》，2016年第6期，第10-21页。该TFP核算模型测度了资本和劳动组合转化为总产出的效率水平。社会经济生产活动的实际产出结果往往与预期存在偏差，徐海红、唐凡：《论绿色发展的内在动力》，《阅江学刊》，2020年第4期，第27-35页。在产生期望产出的同时，也会产生非期望产出（如废气、废水等）。因此，单纯使用期望产出并不能很好地衡量生产过程中污染的负外部性造成的总体社会的效率损失。随着中国经济发展过程中的环境问题不断凸显，基于非期望产出的绿色发展效率核算体系开始广泛应用到中国绿色全要素生产率（以下简称GTFP）的核算研究中。陈诗一：《中国的绿色工业革命：基于环境全要素生产率视角的解释（1980—2008）》，《经济研究》，2010年第11期，第21-34页。虽然现有文献关于GTFP的研究已经比较丰富，但传统GTFP指数核算框架中非期望产出仅包含二氧化碳或二氧化硫的排放量，忽略了该地区主动参与碳汇和碳捕集行为对环境治理效率的影响。因此，传统GTFP核算方法可能已经不适用于碳达峰和碳中和背景下的綠色发展效率测度和评价，并且可能会低估区域绿色发展效率。

总体而言，关于测度气候与环境背景下区域绿色发展水平的文献已经比较丰富，学者们对此问题进行了比较深入的探索，但本文认为仍然可以从两个方面展开进一步研究。第一，中国已经正式向全世界宣布将于2030年前实现碳达峰、2060年前实现碳中和，中国中长期能源政策和环境政策的重点必然包括碳达峰和碳中和目标。相关产业政策的着力点不仅要聚焦碳减排，还应当聚焦碳捕集，这意味着传统的基于期望产出和非期望产出框架的GTFP核算方法已经不能准确测度经济主体（包括微观企业层面和宏观区域层面）的绿色发展效率，缺乏对经济主体碳捕集和碳汇行为的考察。第二，《中华人民共和国国民经济和社会发展第十四个五年规划和2035年远景目标纲要（草案）》提出，深入实施区域重大战略、区域协调发展战略、主体功能区战略，健全区域协调发展体制机制，构建高质量发展的区域经济布局和国土空间支撑体系。在此背景下，长三角地区是中国经济发展最活跃、开放程度最高、创新能力最强的区域之一，将其打造为低碳、零碳绿色高质量一体化发展样板，对于在全国范围推进区域经济高效绿色一体化发展具有重要的示范效应。

因此，本文的贡献主要体现在以下两个方面。第一，在碳达峰和碳中和背景下，根据经济主体兼具碳减排和碳捕集行为的双重政策要求，本文改进了传统GTFP核算框架，将仅包含碳排放的传统非期望产出改进为体现净碳排放的非期望产出，以准确核算经济主体在碳达峰和碳中和政策约束下的绿色发展效率。第二，本文使用空间效率分析方法，对碳达峰和碳中和背景下长三角地区城市GTFP进行测度，并进一步从绿色协同和创新协同双重视角研究长三角地区城市一体化发展问题。后续章节安排如下：第二节为模型设定，探索碳中和背景下的GTFP核算框架，构建Adjusted_GTFP指数;第三节介绍数据来源和数据的处理方法;第四节对长三角地区城市TFP进行测度和评价;第五节为研究结论，并给出政策建议。

二、模型设定

（一）基于碳中和目标调整环境技术函数

假设生产过程中的投入要素为x，x=x1，…，xN∈R+N，产出向量分别为y=y1，…，yM∈R+M和b=b1，…，bI∈R+I，其中y表示期望产出，b表示非期望产出。在传统GTFP核算框架下，学者们普遍使用二氧化碳、二氧化硫、氮氧化物等大气污染排放或污水等水体污染排放作为非期望产出。孙亚男、杨名彦：《中国绿色全要素生产率的俱乐部收敛及地区差距来源研究》，《数量经济技术经济研究》，2020年第6期，第47-69页。党的十八大以来，中国经济社会发展经历了全面绿色转型，环境治理体系建设和生态文明建设取得了很大的成效。高家军：《人类命运共同体视域下全球生态文明建设的系统审视》，《系统科学学报》，2021年第4期，第62-67页。中国在推进全面节能减排、减少温室气体排放的同时，通过植树造林、生态修复等手段提高自然碳汇，推进碳捕集。齐绍洲、柳典、李锴等：《公众愿意为碳排放付费吗？——基于“碳中和”支付意愿影响因素的研究》，《中国人口·资源与环境》，2019年第10期，第124-134页。在国家大力推进碳达峰和碳中和目标的背景下，本文提出调整后的非期望产出（Adjusted Undesirable Output）概念来表示净碳排放量，即b′=b′1，…，b′I∈R+I，其中净碳排放量为b′i=bi-hi，表示碳排放总量bi减去碳汇量和碳捕集量hi。b′i=0表示地区i实现碳中和。

使用Px表示生产可能性集合：

假设投入产出的组合为（xk，t，yk，t，bk，t）。利用数据包络分析（DEA），可得以下带约束条件的生产最大化目标函数：

其中，ztk非负，为每个横截面观测值的权重系数，体现生产技术的规模报酬不变性。

（二）方向性距离函数

方向性距离函数（Directional Distance Function）既可以体现生产可能性集的性质，又能够反映生产过程中产出扩张的方向性。Chung Y H， Fare R， “Productivity and undesirable outputs： A directional distance function approach”，Journal of Environmental Management， vol.51， no.3 （1997）， pp.229-240.基于產出的方向性距离函数可以描述如下：

其中，g=gy，gb是方向向量，表示产出的扩张方向。利用DEA方法求解方向性距离函数，其线性规划方程如下：

当方向性距离函数的值接近于0时，表明该地区的生产正接近生产可能性边界。在生产性距离函数的基础上，可以使用Malmquist-Luenberger指数测度长三角地区城市绿色发展效率。

（三）Malmquist-Luenberger生产率指数

利用Malmquist-Luenberger生产率核算法计算调整后的绿色全要素生产率指数（记为Adjusted_GTFP）：

Adjusted_GTFP指数可以分解为效率变化指数（EFFCH）和技术进步指数 （TECH）：

公式（6）至（8）表明，Adjusted_GTFP指数由两部分构成，其中EFFCH表示在技术条件一定的情况下，实际产出接近生产可能性边界的程度，TECH表示技术水平的变动引起的生产可能性边界的移动。当EFFCH指数和TECH指数大于（小于）1时，表示相对于上一期，生产效率和技术水平提升（降低）。

三、数据来源与数据处理

（一）数据来源

本文研究范围限定为长三角地区的绿色全要素生产率。首先，从空间范围而言，2016年5月国务院发布《长江三角洲城市群发展规划》，明确了规划范围，具体包括上海市，江苏省的南京、无锡、常州、苏州、南通、盐城、扬州、镇江、泰州，浙江省的杭州、宁波、嘉兴、湖州、绍兴、金华、舟山、台州，安徽省的合肥、芜湖、马鞍山、铜陵、安庆、滁州、池州、宣城，共26市。其次，从时间范围而言，本文数据涉及市级层面的GDP、劳动、资本存量、能源投入、二氧化碳排放和二氧化碳吸收多个方面，考虑数据的可获取性，选择2000—2017年为时间窗口期。

城市层面名义GDP、从业人员（劳动）、固定资产投资总额等数据来源于《中国城市统计年鉴》，部分缺失数据参照地方统计年鉴。城市层面的固定资产投资价格指数、国内生产总值指数、居民消费价格指数等数据使用各城市所在省的省级数据进行替代，数据来源于上海、江苏、浙江和安徽相应年份的统计年鉴。城市层面的碳排放和碳吸收数据来自CEADS数据库。感谢CEADS数据库提供支持。CEADS为中国碳核算数据库，专门提供中国及全球其他发展中经济体多尺度能源、排放及社会经济清单，网址为https：//www.ceads.net.cn/。

（二）数据计算与处理

1.要素投入

劳动投入是单位从业人员、私营与个体从业人员的总和，资本投入（资本存量）参考单豪杰使用的永续盘存法进行计算，单豪杰：《中国资本存量K的再估算：1952—2006年》，《数量经济技术经济研究》，2008年第10期，第17-31页。基期的资本存量根据如下公式计算：

2.期望产出

文中期望产出由实际GDP来定义，根据各省市GDP平减指数将各城市GDP调整为2000年不变价格，然后对各市名义GDP进行平减得到实际GDP。

3.调整后的非期望产出

现有文献关于非期望产出的选取指标包括二氧化碳排放、二氧化硫排放、废水排放、固体废料排放等，在相关研究中，还没有统一的标准能够科学全面地反映非期望产出，也没有探讨减排与碳捕集两措并举情形下的净碳排放问题。陈诗一、马倩倩：《基于水污染治理的中国经济转型评估》，《阅江学刊》，2020年第2期，第34-43页。因此，这里使用二氧化碳排放量与自然碳汇、碳捕集的差额来表示调整后的非期望产出。

4.空间权重矩阵

参照经济地理引力模型，假定两地区之间的经济关联不仅受到空间距离的影响，也与各自经济发展水平有关，因此定义Gij=GDPiGDPj d2ij。引力矩阵中的GDP數据是2000—2017年城市实际GDP的平均值，dij表示区域i和区域j之间的地理空间距离。空间权重矩阵Wij构建如下：

5.城市绿色效率中心度

根据长三角地区城市空间权重矩阵Wij和调整后的城市绿色全要素生产率指数向量Adjusted_GTFPi，构建长三角地区城市绿色效率中心度指标Zi如下：

根据公式（10），城市绿色效率中心度指标Zi处于0，1区间。当Zi→0时，表示城市绿色效率中心度较低;当Zi→1时，表示城市绿色效率中心度较高。

四、数据结果

（一）碳中和背景下长三角地区城市Adjusted_GTFP测算

根据Malmquist-Luenberger生产率核算法，使用Stata16.0软件对碳达峰和碳中和背景下长三角地区26个城市的Adjusted_GTFP指数进行计算，并对测算结果按降序排列，如表1所示。

由表1可见，总体而言，长三角地区城市Adjusted_GTFP指数的波动幅度不大，稳定在[0.892，1.042]区间。就单独的城市而言，2000—2017年，上海、扬州、嘉兴、杭州和南京的Adjusted_GTFP指数排名靠前，台州、滁州、宣城、安庆和池州的Adjusted_GTFP指数排名靠后。在地理上靠近上海的城市（如嘉兴、杭州、南京和苏州），其Adjusted_GTFP指数相应较高，而在地理上远离上海市和本省省会（南京、杭州和合肥）的城市（如台州、滁州、宣城、安庆和池州等），其Adjusted_GTFP指数相应较低。这个结果表明，2000—2017年，长三角城市群绿色发展效率表现出空间关联特征，即在绿色发展和创新发展方面具有一定的协同性。

根据调整GTFP的测度理论框架，碳达峰和碳中和背景下长三角地区城市Adjusted_GTFP指数出现差异可能有三个方面的原因：第一，纯技术因素变动，由TFP衡量;第二，绿色发展效率变动，由GTFP衡量;第三，碳达峰和碳中和政策背景下，自然碳汇和碳捕集活动引起的生产效率变动，由Adjusted_GTFP衡量。因此，为了进一步研究碳达峰和碳中和背景下长三角地区城市Adjusted_GTFP指数产生变化的原因，有必要对各个城市基于不同TFP核算口径的数据进行比较，结果如表2所示。

表2表明：首先，综合对比TFP、GTFP和Adjusted_GTFP核算口径下的生产效率指数，发现TFP、GTFP和Adjusted_GTFP核算指数存在很强的一致性，即Adjusted_GTFP指数较高（低）的城市，其TFP和GTFP指数也比较高（低）。这意味着，在碳达峰和碳中和背景下的Adjusted_GTFP指数主要受到纯技术变动和绿色发展效率变动的影响。其次，对比长三角地区26个城市的Adjusted_GTFP指数与TFP指数和GTFP指数的数值，发现总体呈现Adjusted_GTFP>GTFP>TFP的规律。该结果表明，在长三角地区，城市的绿色发展效率普遍为正（由GTFP>TFP可得），长三角地区的城市在推进技术发展的同时，其绿色发展效率也得到了更大幅度的提升;同时，根据Adjusted_GTFP>GTFP可以判断，仅以传统非期望产出作为生产效率的测度标准会低估长三角地区城市绿色发展效率，在碳达峰和碳中和背景下，使用Adjusted_GTFP指数能够更加真实地反映一个地区的实际绿色发展效率。

（二）进一步研究：Adjusted_GTFP视角下的长三角一体化

莫兰指数（Moran Index）是衡量地理单元之间空间关联性的指标。考虑空间序列aiIi=1，空间莫兰指数的计算公式为：

其中，S2表示样本方差，Wij表示空间权重矩阵，表示空间序列aiIi=1的均值。如果莫兰指数为正，则表示各个地理单元之间存在正向的空间关联性。本文使用莫兰指数检验发现，区域全局莫兰指数为0.270，并且在1%的显著性水平下通过检验，说明基于Adjusted_GTFP指数核算的长三角地区城市绿色发展效率存在显著的空间正向关联。因此，本文使用长三角地区26个城市Adjusted_GTFP指数测算结果，制作了长三角地区城市Adjusted_GTFP指数莫兰散点图，如图1所示。

图1表明，长三角地区26个城市样本点基本都聚集在莫兰散点图的第一象限和第三象限，并且表现为显著的正向空间关联，这意味着绿色发展效率高的城市对邻近城市具有正的绿色发展效率溢出，能够带动邻近城市绿色发展效率的提升，即在基于Adjusted_GTFP指数的长三角地区城市绿色发展效率核算框架下，长三角城市群呈现一体化协同发展特征。

很多经验证据和实证研究表明，长三角地区城市表现出较强的一体化协同发展特征，李廉水、周彩红：《区域分工与中国制造业发展——基于长三角协整检验与脉冲响应函数的实证分析》，《管理世界》，2007年第10期，第64-74页。但是对长三角地区一体化协同发展的系统协同机制和协同框架缺少深入的探索。因此，接下来本文使用城市绿色效率中心度指标，利用城市层面数据，分析在长三角地区一体化协同发展中哪些城市扮演了绿色创新发展增长极的角色，哪些城市在一体化协同方面仍然存在不足，如何进一步提升长三角地区的一体化协同水平。

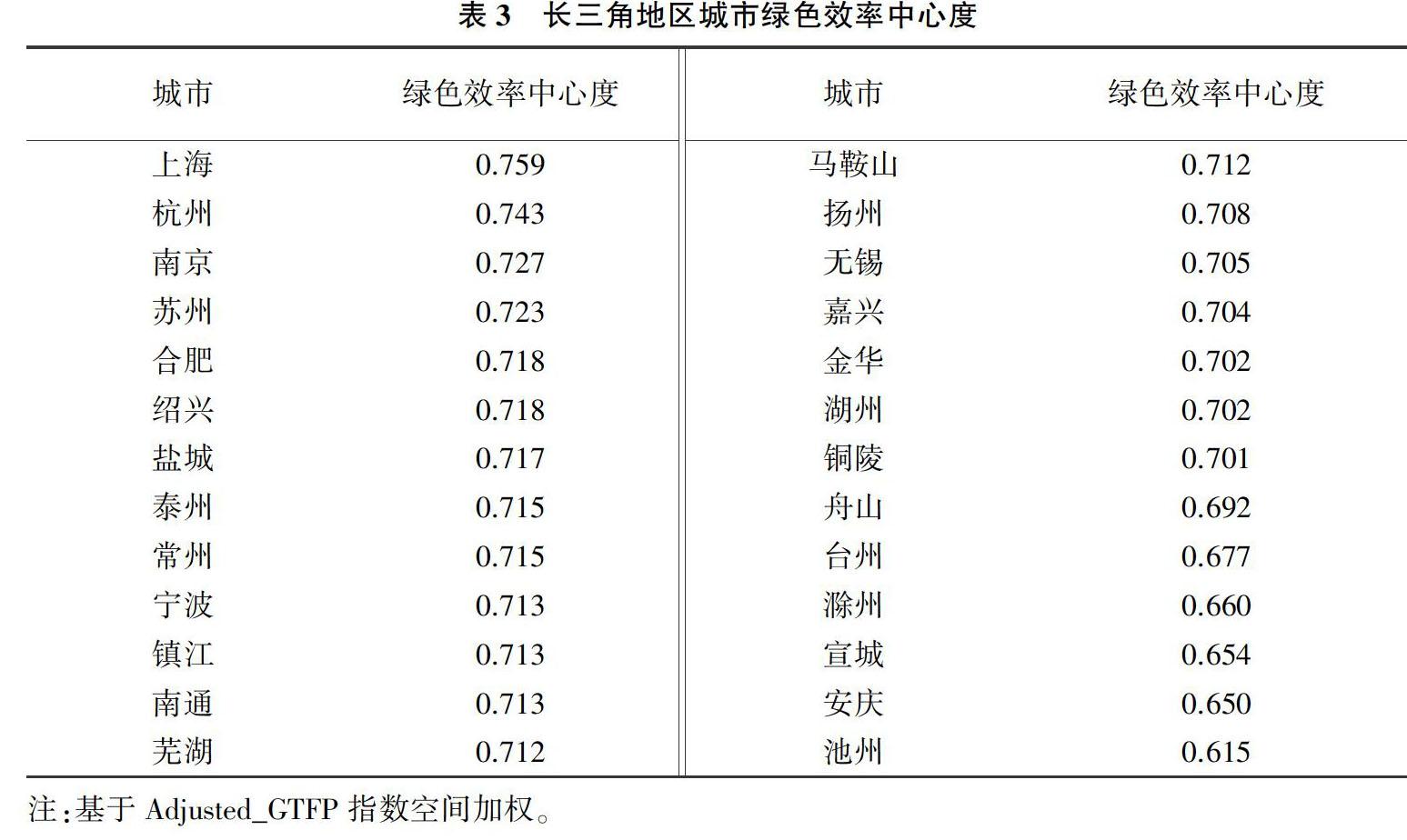
根据公式（10）构建的城市绿色效率中心度指标，本文使用空间权重矩阵Wij和Adjusted_GTFP指数计算得到长三角地区26个城市的绿色效率中心度测算值，按照降序排列，结果如表3所示。

根据表3的数据，上海、杭州、南京、苏州和合肥的绿色效率中心度测算值排名靠前，而台州、滁州、宣城、安庆和池州的绿色效率中心度测算值排名靠后。通过数据分析，可以得到如下结论。第一，区域性中心城市的绿色效率中心度高于其他城市，上海市和浙江、江苏、安徽三省省会城市的长三角地区绿色效率中心度排名较高，意味着在长三角协同一体化过程中，区域性中心城市扮演了绿色创新发展增长极的角色。第二，从区域性结构差异来看，城市绿色效率中心度指标存在显著的省际差异。比较江苏、浙江和安徽三省，江苏省的平均排名高于浙江省，安徽省最低。在各省内部，也存在各自的绿色创新增长极，使整个长三角地区呈现“多核共进”的协同发展特征。

五、结论与政策建议

（一）结论

本文研究碳达峰和碳中和背景下，长三角地区城市GTFP核算和区域经济一体化发展问题。基于Malmquist-Luenberger生产率核算方法，本文改进了非期望产出的传统定义，使用碳排放减去碳捕集（即净碳排放）替换碳排放指标，构建Adjusted_GTFP核算框架。基于 Adjusted_GTFP核算框架，使用2000—2017年长三角地区26个城市的碳排放和碳捕集数据进行测度，主要结论如下。第一，对比Adjusted_GTFP指数，GTFP指数使得长三角地区城市绿色发展效率被低估，说明在碳达峰和碳排放背景下，Adjusted_GTFP指数能够更科学准确地反映地区绿色发展效率。第二，长三角地区城市之间的绿色发展效率存在正向的空间关联，绿色发展效率高的城市对邻近城市具有正的绿色发展效率溢出，能够带动邻近城市绿色发展效率的提升。第三，长三角地区城市绿色发展效率存在显著的“多核共进”的协同发展特征，江苏省、浙江省和安徽省的省会城市在长三角内部的绿色发展方面发挥了区域性协同作用。

（二）政策建议

基于上述研究结果，本文从三个方面提出推进长三角地区绿色协同一体化的政策建议。第一，建立健全碳排放、碳捕集数据的统計核算体系。在中长期范围内，碳达峰和碳中和将是中国产业发展政策关注的重点内容，对企业实行“碳考核”，不仅需要关注企业的碳减排行为，也需要关注企业的碳捕集行为对净碳排放的影响。在健全碳排放、碳捕集数据统计核算体系的基础上，再进一步对全社会的生产活动进行精准化的“碳治理”。第二，优化区域经济空间布局，推进长三角城市一体化发展迈上新台阶。虽然长三角地区城市的绿色发展效率存在正向的空间关联，但仍然具有区域结构性不平衡效应，因此，需要充分挖掘区域性中心城市的辐射带动潜力，促进资源要素跨区域有序自由流动，加强区域之间（尤其是省之间）的政策互补性和协同性。第三，统筹促进经济发展、保护生态环境与应对气候变化的关系，提升长三角地区生态韧性与发展韧性。多渠道建立政府、企业、公众广泛参与应对气候变化的行动机制，探索“链长制”治理模式在碳治理方面的应用，从生态链与产业链层面加强长三角地区的生态韧性和产业发展韧性。〔责任编辑：沈 丹〕