基于Simulink的有限转角电机控制系统建模与研究*

罗文龙，周 骅，赵 麒，朱文龙

（1.贵州大学大数据与信息工程学院，贵阳550025；2.贵州民族大学机械电子学院，贵阳550025）

1 引言

电机作为运动控制中最常用的执行器，广泛应用于工业各个领域以及人们的日常生活中。有限转角电机是在精准定位的情况下可在一定角度范围内驱动负载的无刷直流电机[1]。它利用电子换向装置代替机械换向装置，结构相对于直流电机更为简单，工作更为稳定，同时具有比交流电机更好的调速性能，控制精度更高，因此常被用于高性能的有限角度驱动器，在工业各个领域有着广泛应用，所以对其控制系统的要求也越来越高。在设计控制系统时，既要考虑成本、开发周期等问题，又要对控制性能有较高的要求。对有限转角电机控制系统进行建模和研究，通过模型仿真来测试控制效果，既能节省人力物力，又方便对系统进行优化改进[2]。

2 有限转角电机建模

有限转角电机是一种特殊的无刷直流电机。可以根据无刷直流电机的数学模型得到有限转角电机的数学模型。

2.1 绕组电压方程

在理想条件下，根据基尔霍夫电压原理得到无刷直流电机绕组电压平衡方程[3-4]如下：

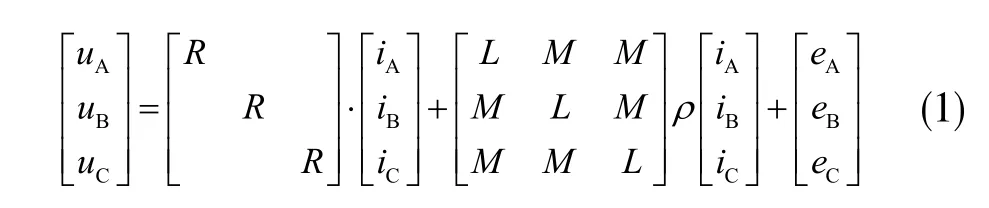
式中：uA、uB、uC为三相电机绕组的端电压；iA、iB、iC为电机的绕组电流；eA、eB、eC为反电动势；R为电机绕组电阻；L为相绕组电感；M为每两相绕组间的互感；ρ为微分算子d/dt。

此处建模的有限转角电机是单项电机绕组，电压电流都只有一项，不存在绕组间的互感M，只存在绕组电感L。可根据式(1)得到有限转角电机的电压平衡方程：

以及电机反电动势表达式：

其中ke为反电动势系数，ω为电机转动角速度。根据上述方程，在Simulink里建立电压方程模块，如图1所示。

图1 绕组电压方程模块

2.2 电磁转矩与电机运动方程

根据电磁转矩方程，可得到电机的电磁转矩：

式中，KT为电磁转矩系数。由此式可见电磁转矩与电流i成正比。在考虑负载转矩的情况下，电机机械运动方程[5-6]为：

式中，J为转子负载的转动惯量；D为粘性阻尼系数；k为弹簧的刚度；T为电磁转矩；ML为负载转矩。可知，电磁转矩与负载转矩经过加、乘运算后再通过积分模块可得到角速度，再对角速度做积分即可得到角度位置信号。再对上述方程在Simulink里建立方程模块，如图2所示。

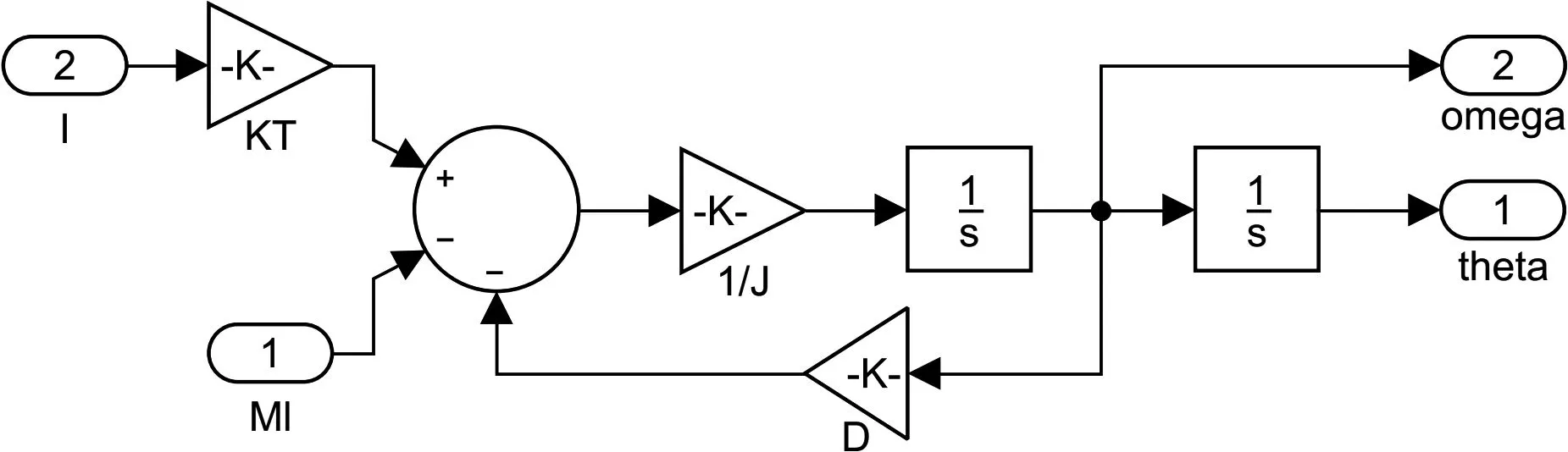
图2 电磁转矩与机械运动方程模块

将图1、图2的两个模块相连，得到电机整体模型，如图3所示。由机械运动模块获得的角速度通过反电动势系统的乘法模块输入到电压平衡模块，并且由电压平衡模块得到的电流通过电磁扭矩的乘法模块得到电磁扭矩。电机模型整体封装后的状态如图4所示。

图3 有限转角电机整体模型

图4 有限转角电机模型封装

3 电机控制系统

电机控制系统主要由三环PID、前馈系统、PWM和电压逆变器模块组成，如图5所示。指令位置与有限转角电机的位置反馈的差值作为位置环输入，而位置环的输出与前馈增益和速度反馈的差值作为速度环的输入。速度环的输出与速度反馈的差值经过速度环PID调节和PWM模块，转化为PWM波形并经过H桥模块来控制调节电机。

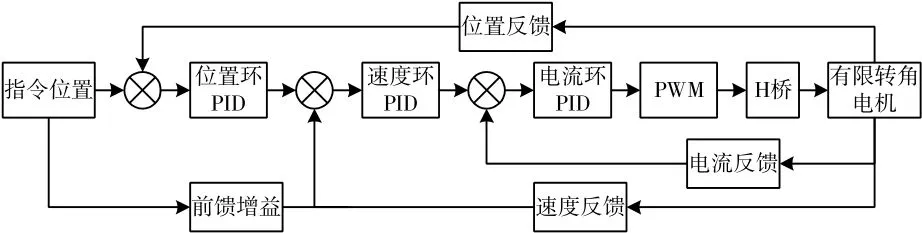
图5 电机控制系统框图

3.1 PID闭环控制

PID控制由比例控制（Proportional）、积分控制（Integral）和微分控制（Derivative）组成。其输入是由电机反馈的值与给定的理想值决定的，而输入经过PID调节后的输出又反过来作用于电机，这个控制过程称为闭环控制。

本电机控制系统采用电流环、速度环、位置环三闭环控制系统。电流环作为第一环，是由于PID的调节即是根据电动机反馈的电流进行的，电动机输入电流接近设定的理想值，在转矩模式下，由电流环控制电动机的转矩，因此该环的运算最小且动态响应最快；速度环作为第二环，其输入为第一环的输出与反馈电流的差值；位置环作为最外环，其输入为给定的理想位置，在位置环控制模式下，系统执行了所有三个环计算，所以其运算响应的时间较长[7-8]。

3.2 PWM生成模块

电动机的调速可以通过控制电枢电压实现。电压容易做到连续调节，便于实现无级调速，平滑性好，调速损耗小，电机运行效率高。PWM波就是通过改变电压大小来控制直流电机转速的调制电波，通过改变一个方波在一个给定周期中占有的时间长度，可以得到一个可变的有效电压输出。占空比是指导通时间（即高电平时间）在整个周期所占的百分比，即：

式中t为高电平持续时间；T为波形的周期。平均电压为：

式中，通常情况下，VL取0。平均电压与占空比成正比。由于信号在高电平与低电平之间切换非常快，所以负载仅能识别电压的平均值。本系统得到占空比输出公式为：

其中Vref是输入电机两端的电压；Vmin为最小参考电压；Vmax为最大参考电压。当Vref=Vmin时，占空比最小为0；当Vref=Vmax时，占空比最小为100。

3.3 前馈系统

有限转角电机要求系统具有高增益，以保证系统具有良好的快速性、稳定性、准确性，以及抗干扰能力。然而，增益过高可能引起不稳定，特别是PID控制器中的积分控制器增益。而在传统PID控制中，仅当出现一个位置跟踪误差，就给电机发送一个运动指令，即系统仅会在以及落后于期望轨迹之后才会采取行动。这就导致电机的上升时间、超调量等动态响应性能不够理想，因此此处根据期望轨迹计算需要的速度，将其直接送到速度环而不必等待先产生一个误差，即加入前馈系统对控制进行优化。

当速度前馈增益为Kvff时，前馈方程为：

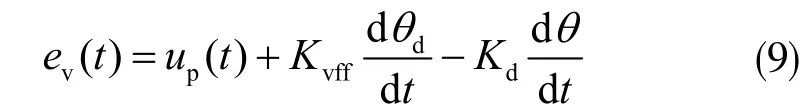
式中，up(t)是位置环的输出，Kd为电机反馈回来的电流增益。

速度前馈可以消除跟踪误差，然而，如果Kvff增益值设置得太高，速度前馈会引起超调，因为Kvff增益值设置得太高，在速度曲线的加/减速区间会产生大的误差尖峰；而Kvff增益值过低，则会导致跟踪误差过大，即超调量较大，所以需要进行多次仿真实验来整定Kvff前馈增益值。

除了包含如前所述各模块以外，还利用switch模块实现H桥的功能来决定控制电机的电压的方向。根据上述原理，在Simulink里建立电机控制系统模块，如图6所示。

图6 电机控制系统模块

4 仿真分析

在Simulink上搭建有限转角电机及三环PID控制系统。其中电机模型里驱动线圈电阻为0.52Ω；线圈电感为7.68mH；反电动势常数为0.181；给定的理想位置响应为初始值为1s时间内由0变为1的阶跃响应。在经过大量仿真调试后，三环PID控制系统最终控制参数确定为：

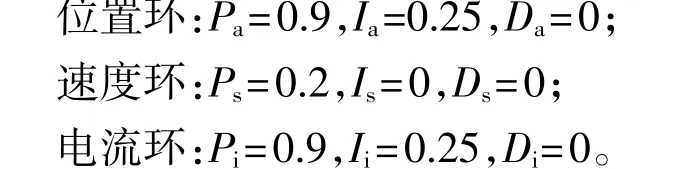
仿真结果如图7所示。经分析可知，相比于传统三闭环PID控制系统，加入前馈的三闭环PID控制系统提高了系统的动态性能。调节时间即上升时间为0.7s，远小于传统PID的3.5s，相当于传统PID最大超调量的15.8%。前馈消除了跟踪误差，没有产生超调现象，电机系统能更快地将电机调节至稳定状态。可见，具有前馈系统优化的三闭环PID控制系统控制性能良好，明显优于传统PID的表现。

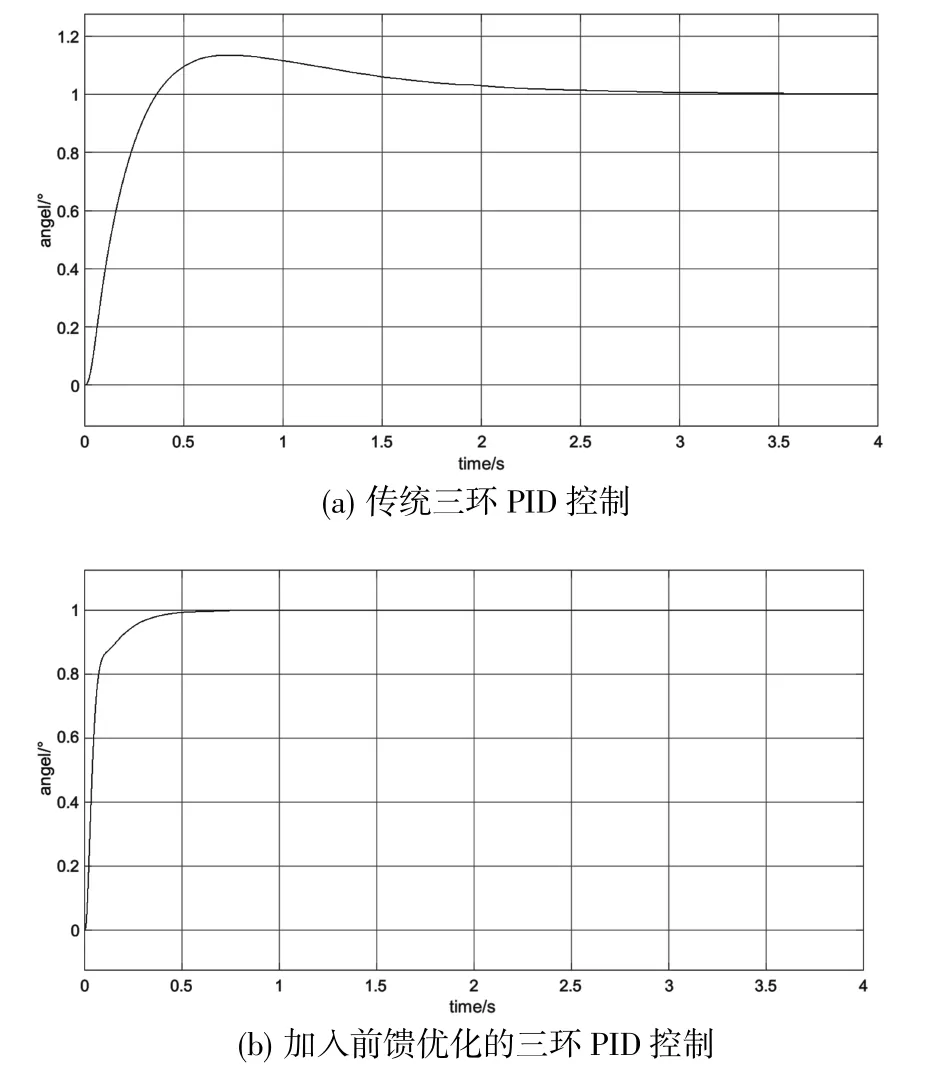
图7 仿真结果对比

5 结束语

根据有限转角无刷直流电机工作原理和特点，分析了无刷直流电机的数学模型，依据PID控制原理，在MATLAB的Simulink模块里完成对有限转角电机的建模，加入前馈系统对三环PID控制系统进行了优化。在调整参数并进行仿真后，该控制系统不仅没有出现超调现象，而且控制性能稳定，动态指标良好，控制效果已超越了传统三闭环PID控制系统。该设计目前已应用于某些有限转角电机控制的实际应用中。