强夯荷载作用下填土地基的动力特征分析

邱玉航

(福建工程学院，福州 350001)

1 概 述

随着我国经济的快速发展，我国的基础建设也日益完善，但随之而来的问题是土地资源短缺。因此在城市化的进程中，一些工程不可避免的会在性质较差的地基上修建。为了保证施工的安全进行和后期的正常使用，必须先对这些不良地基进行加固。迄今为止，能够对不良地基进行加固的方法有很多种，但其适用条件都大不相同。强夯法是由法国工程师L. Menard率先提出的[1]，强夯法起初只用来加固砂土和碎石土地基。因为强夯法具有设计简单、施工简便、经济性强等优点，并且随着人们对强夯法加固机理的认识日益完善，其适用的范围也扩大到湿陷性黄土、低饱和度粉土、黏土等地基。目前，已有大量学者对强夯法的加固机理进行了研究。王成华[2]采用等效静力法对强夯作用下土体中的应力分布情况进行了研究，并总结了其分布的规律。Q. Gu等[3]运用有限元方法，对强夯法加固地基土时土中复杂的应力分布情况进行了有效的预测，并在此基础之上，综合分析了影响强夯法加固效果的主要因素，进而总结出相应的图表，用来指导以后的施工。朱继永等[4]、李本平[5]、吴铭炳等[6]编制了有限元程序，对强夯法加固地基土时土中的动应力分布进行了模拟。宋修广等[7]运用修正的动态有限单元计算程序，准确得出强夯作用下地基土中的动力响应。

综上所述，强夯法无论是在理论研究还是工程实践方面都有较好的发展，但强夯法的理论发展还是要落后于工程实践的，强夯法的施工参数都是根据类似的施工经验来确定的，不够系统和完整。因此，本文运用有限元方法对强夯时地基土中的动应力、位移等特性进行系统分析，以期为强夯法加固类似填方地基工程提供参考和依据。

2 计算模型的建立

2.1 数值模型

根据强夯影响范围的经验值，选取模型的尺寸为30 m×30 m×20 m，夯锤直径为2 m。考虑到模型的对称性，取四分之一模型进行建模，并在两个对称面上施加对称约束，顶面为自由界面，底部为固定约束，其余两个侧面只约束水平向的位移，在两倍夯锤直径的范围内对网格进行加密处理，以保证计算结果的准确性，模型示意图见图1。在ABAQUS有限元软件中，一阶单元能够更好地模拟应力波在土体中的传播[8]，因此地基土采用线性的三维八节点实体减缩积分单元(C3D8R)，本构模型采用Mohr-Coulomb理想弹塑性模型，具体的土体参数见表1。在实际工程中，每一次的夯击都会使土体的弹性模量有所提高，因此本文在模拟土体弹性模量随夯击次数的变化规律按照以下经验公式[9]来确定。

表1 地基土材料参数表

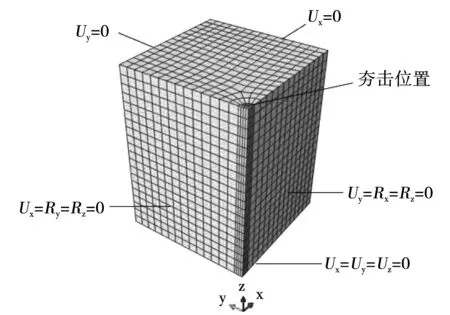
图1 模型示意图

E=E0×N0.516

(1)

式中：E为土体夯击N次之后的弹性模量；E0为土体的初始弹性模量；N为夯击次数。

2.2 强夯荷载的确定

现有研究结果表明[10-12]，夯锤夯击地面过程中产生的应力波只有一个波峰，作用时间仅为0.04～0.2 s。本文主要目的是研究动应力在地基土中的分布，因此本文忽略夯锤的自由下落过程及夯锤与土体的相互作用，将强夯荷载简化为三角形荷载直接施加在地基土表面，以此来模拟夯击的过程，见图2。

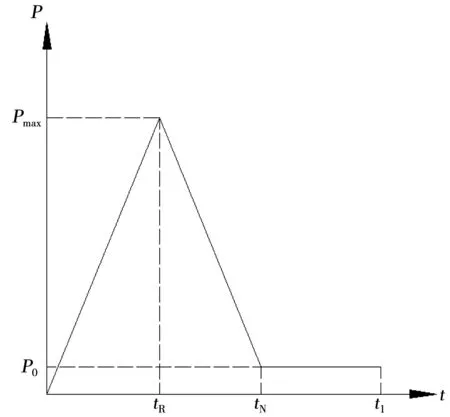
图2 强夯冲击荷载示意图

图2中各参数按照以下公式计算：

(2)

(3)

(4)

(5)

式中：Pmax为峰值应力；P0为夯锤的自重应力；tN为冲击荷载作用时间；v为夯锤冲击地面时的速度；m为夯锤的质量；r为夯锤半径；S为弹性常数。

3 计算结果分析

3.1 地基土中的动应力变化

本文描述了地基土在第一次夯击之后土中应力和位移等动力特性的变化情况，夯击能的大小为2 000 kN·m。为了直观展现出动应力在地基土中的传播过程，图3展示了2 000 kN·m夯击能作用下，不同时刻竖向应力的分布云图。从图3中可以看出，动应力的分布呈现出梨形，地基土中的动应力以夯锤为中心，逐渐向四周扩散，这与目前一些学者的研究结果类似。随着时间的推移，动应力沿水平方向扩散的速度要大于沿竖向扩散的速度，而且动应力的最大值始终位于夯锤作用位置的中心线上。

图3 地基土中的竖向应力变化云图

图4和图5分别为位于夯点中心下不同深度和地表距离夯点中心不同距离处的动应力变化曲线。

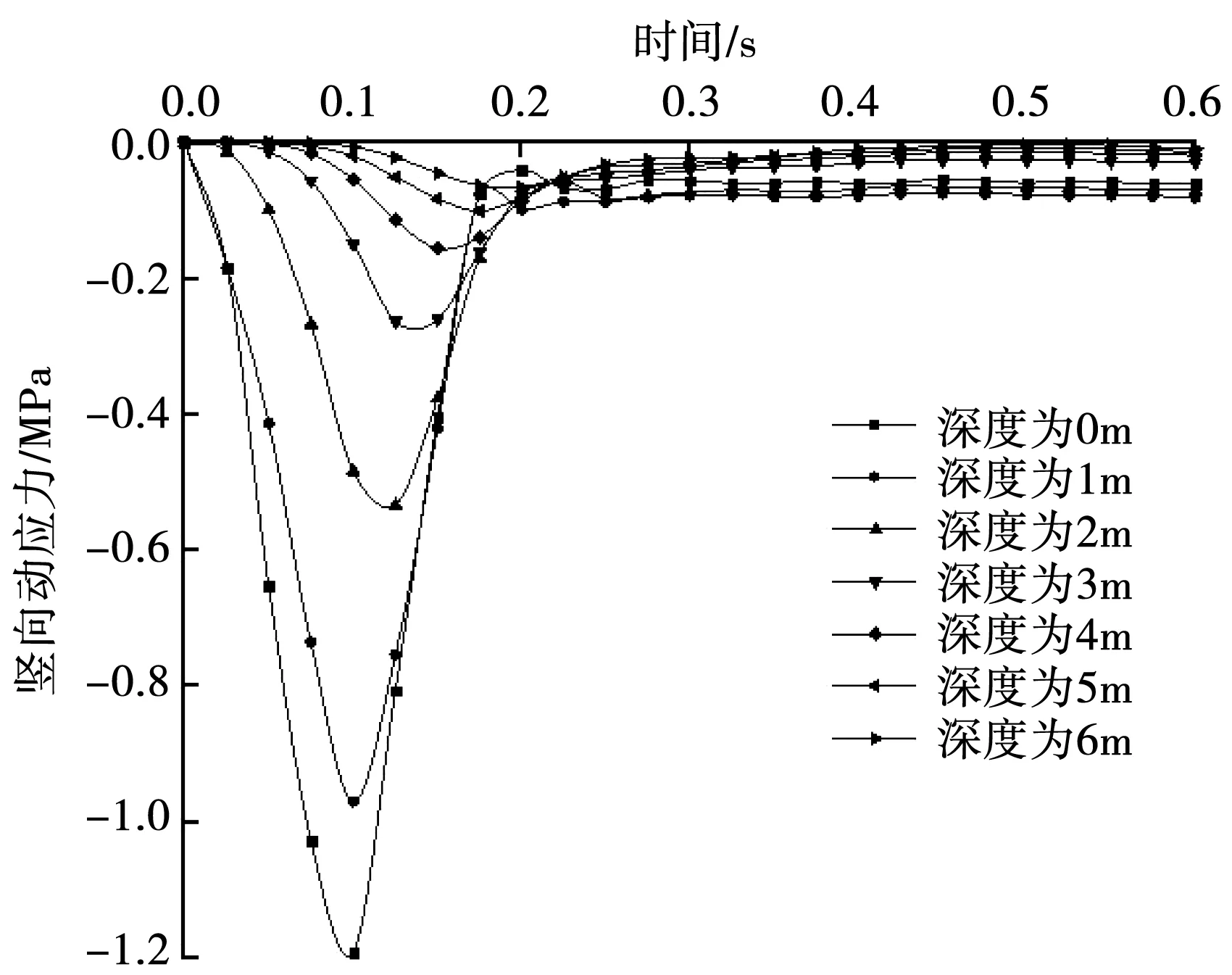
图4 不同深度处土中的竖向应力变化曲线

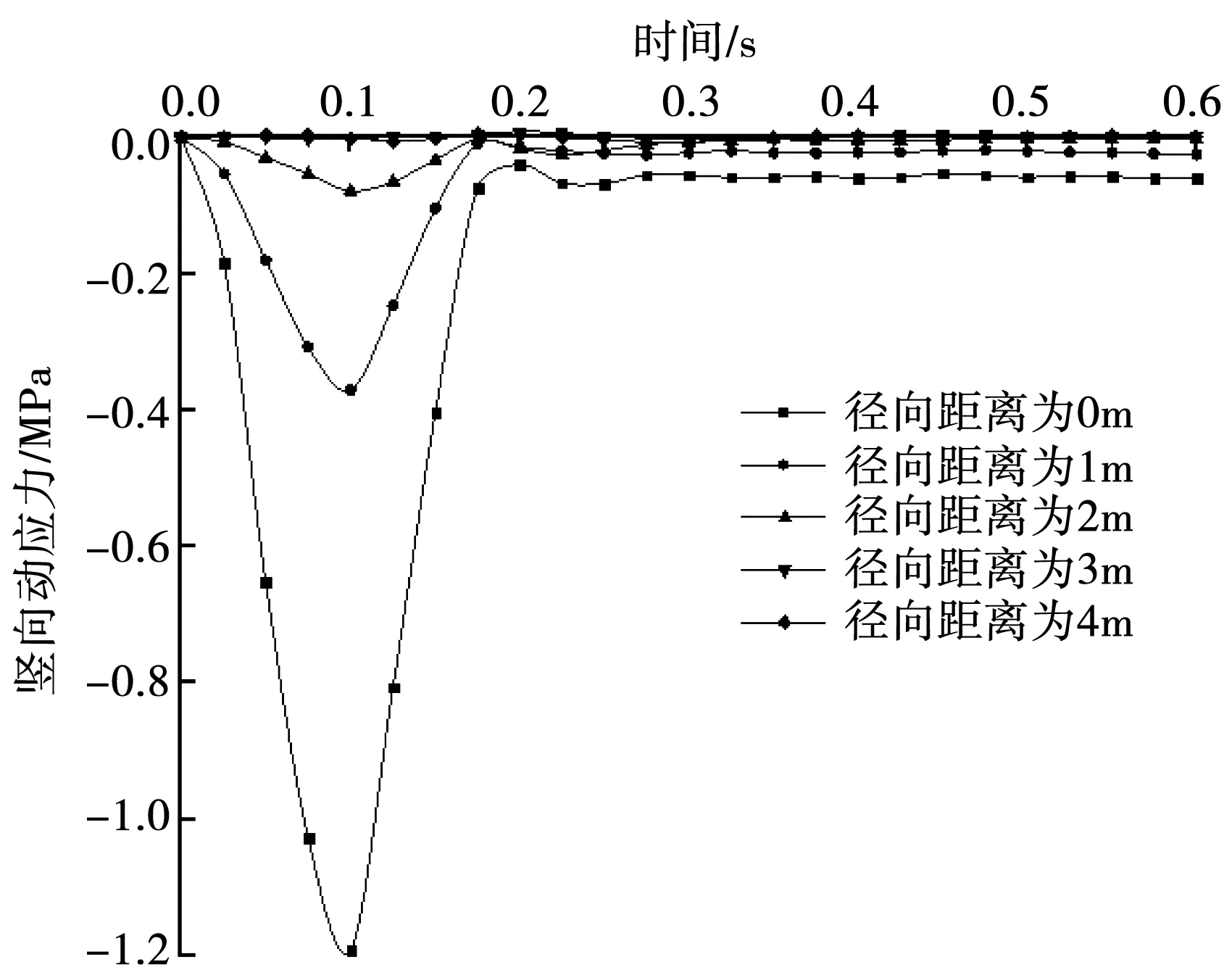
图5 不同径向距离处土中的竖向应力变化曲线

从图4和图5中可以看出，强夯产生的应力波只有一个波峰且持续的时间较短，在0.4 s左右地基土中的应力已不再发生变化，这要远小于实际工程中的夯击间隔时间，因此不用考虑动应力的叠加问题。在不同深度处应力波峰的出现时间也不相同，并且会随着深度的增加而向后推迟，相邻深度处波峰出现的时间差约为0.02 s。然而在地表距离夯点中心不同距离的地方，其应力波峰基本上在同一时间点出现，该现象再一次说明动应力沿水平方向扩散的速度要大于沿竖向扩散的速度。从动应力的衰减速度上看，仍然是水平向的衰减速度要更快一下，这意味着强夯法对夯锤下方土体的加固效果要优于对侧面土体的加固效果。此外，从图4和图5中还可以看出，当深度为6 m时，地基土中的动应力随时间的变化已经不是很明显；当地表与夯点中心的距离超过3 m时，动应力同样不会随着时间的推移而产生波动，这说明2 000 kN·m夯击能在第一次夯击后，其竖向影响范围约为6 m，水平向的影响范围约为2～3 m。

3.2 地基土中的位移变化

图6为强夯法作用下不同时刻地基土的竖向位移变化云图。在夯锤所产生的冲击力作用下，土体产生了较大的竖向位移，使较为松散的土颗粒区域密实，从而起到加固地基的效果。从竖向位移云图中可以看出，土体的竖向和水平向都得到加固，其形状也接近梨形，但竖向加固范围要大于水平向的加固范围，第一击时竖向加固深度约为5～6 m，而水平加固范围约为2倍垂径，即为2 m。

图6 地基土中的竖向位移变化云图

图7为夯点中心以下不同深度处的竖向位移随时间变化的曲线。从图7中可以看出，随着深度的增加，土体的竖向位移也会逐渐减小，土体的竖向位移在达到峰值之后会有一定的回弹，而且不同深度处土体的位移峰值和动应力的峰值几乎同时出现。这说明土体竖向位移达到最大值的时间同样会随着深度的增加而推后，也说明了地基土中存在脉冲应力波，符合动应力在土中的传播特性。此外，在深度为6 m时，地基土的最终位移约为18 mm，位移的变化情况也不够明显，说明传播到该深度处的夯击能较少，夯击能在迅速衰减。

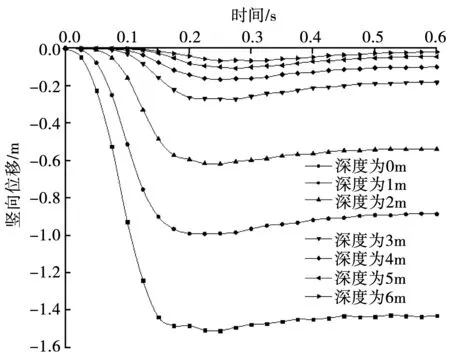
图7 不同深度处竖向位移变化曲线

图8为地基表面距夯点中心不同距离处的竖向位移变化曲线。从图8中可以看出，在距离夯点中心3 m位置处，地基土有轻微隆起，这也是符合工程实际的，说明本文模拟方法的可行性。通过与图6进行对比，再次印证夯击能沿水平向衰减的速度更快，在水平距离达到2 m时，竖向位移的变化相对微小。

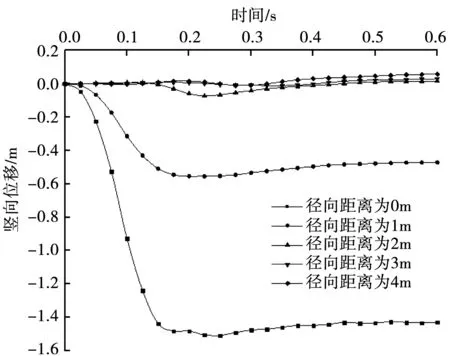
图8 不同径向距离处竖向位移变化曲线

图9为不同径向距离处水平位移随深度的变化曲线。从图9中可以看出，深度为0～3 m范围内的水平位移较大，并且在该深度范围内水平位移的下降速率也较大。这说明夯锤产生的夯击能量大部分被该深度处的土体所吸收，因此0～3 m深度处的土体加固效果最好。当深度大于3 m之后，不同径向距离处的水平位移变化速率趋于一致。在径向距离为5 m的位置，其最大的水平位移约为0.04 m，该值相对较小，因此可以认为夯击位置的水平间距不应大于5 m。

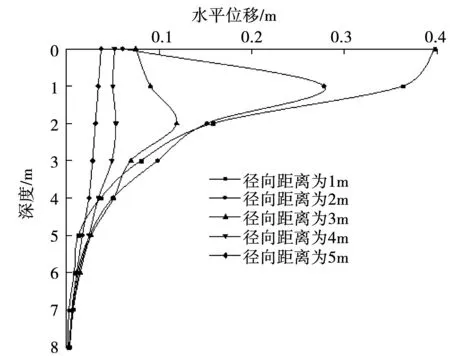
图9 不同径向距离处水平位移变化曲线

3.3 地基土中的振动速度和加速度分析

图10-图13为地基土不同位置处的地基竖向速度和竖向加速度随时间变化曲线。从图10-图13中可以看出，地基土的振动速度和振动加速度的变化规律相似。随着深度的增加，地基土竖向速度和竖向加速度的峰值也有明显的衰减，并且不同深度处的峰值也不是在同一时间点出现，这与动应力的变化曲线类似。在深度为6 m的位置竖向速度和竖向加速度值较小，说明深度在6 m之内的土体受到主要的冲击振动作用。另一方面，随着径向距离的增加，土体的振动时间也会有所增加；地基土的竖向速度沿径向衰减效果要更加明显。

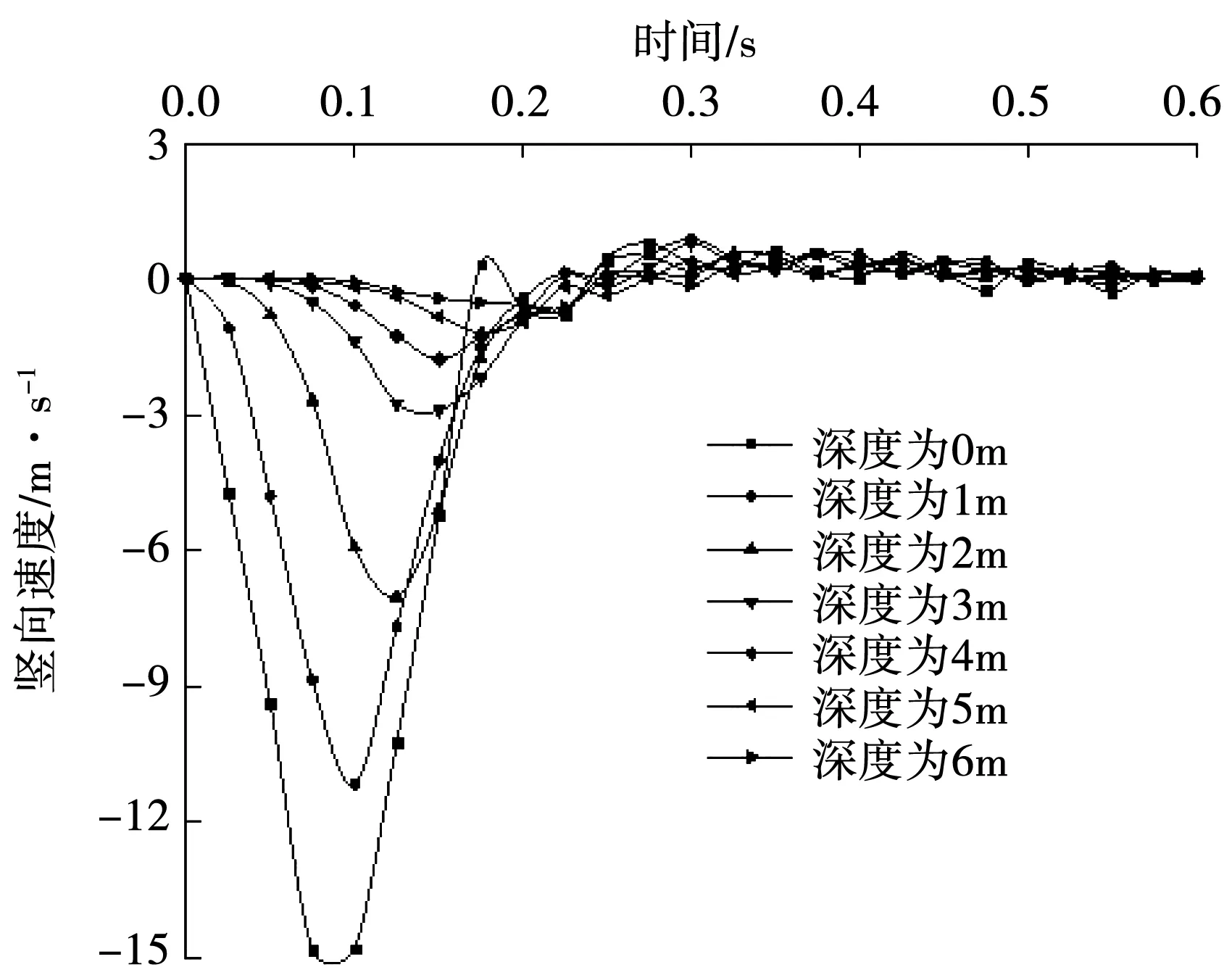
图10 不同深度处竖向速度变化曲线

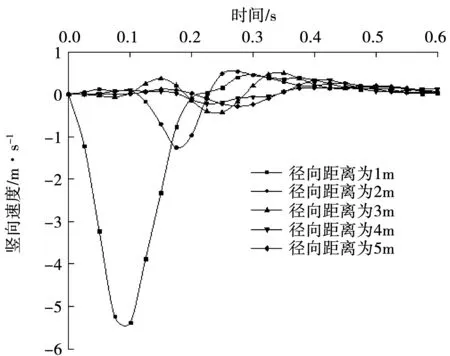
图11 不同径向距离处竖向速度变化曲线

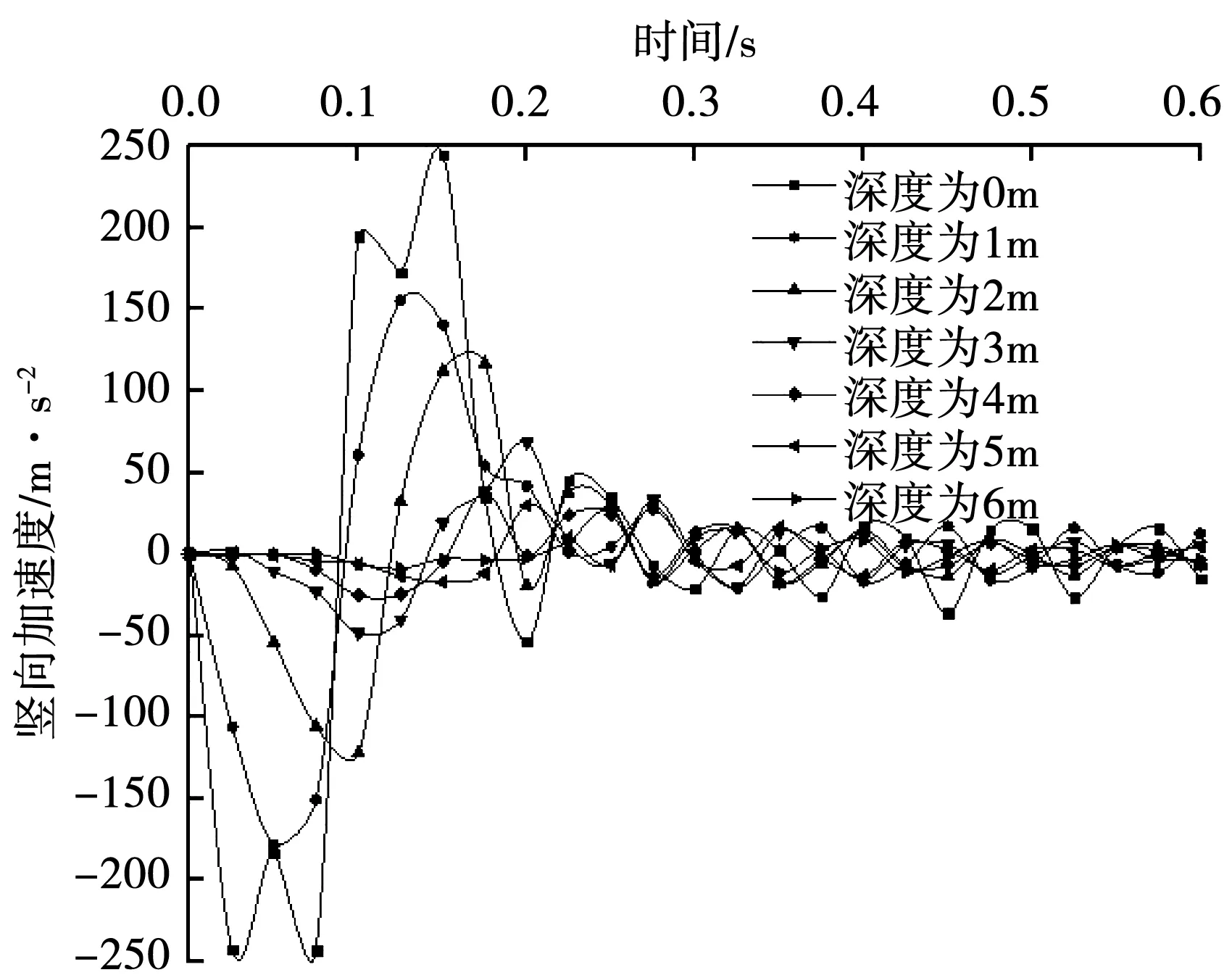
图12 不同深度处竖向加速度变化曲线

图13 不同径向距离处竖向加速度变化曲线

图14是距离夯击中心6 m处，分别在3种不同夯击能的作用下土体竖向振动速度峰值随夯击次数的变化曲线，夯击能的大小分别为2 000、3 000和4 000 kN·m。随着夯击能的增加，土体竖向速度的峰值也会增加，并且振动速度的峰值也会随着夯击次数的增加而增加。但在前6次夯击过程中，土体的振动速度峰值提升较快；当夯击次数超过6次之后，振动速度的峰值趋于稳定。这说明在前6次的夯击中，地基土吸收了大部分的夯击能，导致土体产生塑性变形，随着土体不断被加固，其吸收的夯击能逐渐减少，也就导致了土体的振动速度峰值会随着夯击次数的增加而增加。从另一方面来说，采用强夯法加固地基土时，并不是夯击次数越多越好，而是存在一个临界值。

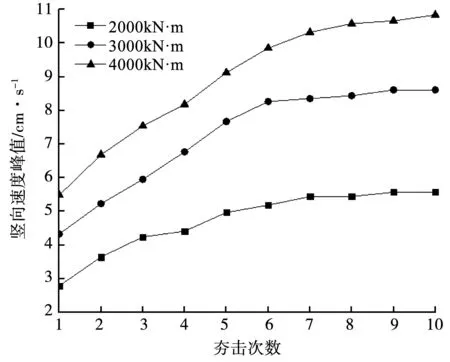
图14 竖向速度峰值随夯击次数的变化曲线

4 结 论

本文运用有限元软件ABAQUS对填土地基强夯过程中土体的动应力、位移、速度和加速度的变化规律进行了分析，得到的结论如下：

1) 强夯作用下土体的动应力分布云图和竖向位移分布云图显示，强夯法的加固范围呈梨形，根据动应力的分布和竖向位移的变化情况可以有效估算强夯的加固范围和夯点间距。

2) 土体的振动速度、振动加速度均会随着土体的深度和径向距离的增加而减小，并且随着夯击次数的增加，振动速度的峰值先增高，随后会趋于一稳定值，该变化规律可以用来确定最佳夯击次数。

3) 强夯所产生的能量是以波的形式在土中传播，夯击能沿径向衰减的速率要大于沿深度衰减的速度。强夯时，土体的动应力、位移、振动速度和振动加速度的峰值出现时间均会随着深度的增加而有所推迟，峰值大小减小。