改进的DDPG算法在机器人路径规划中的应用①

张 宁, 葛 斌

(安徽理工大学计算机科学与工程学院,安徽 淮南232001)

0 引 言

随着机器人技术和自动化的发展,移动机器人被广泛应用于工业、农业和家庭环境中[1]。路径规划问题是移动机器人技术的一个重要环节。在许多实际应用场景下,路径规划往往是在未知环境中进行,如矿井救援、水下机器人控制、资源勘探等。在未知环境下无法获知障碍物的全部信息,只能感知环境的部分信息,所以机器人在未知环境下的路径规划比已知环境更为困难。对于路径规划有一些传统的方法,粒子群算法[2],蚁群算法[3]。这些算法虽然可以实现路径规划,但是不具备环境适应性,需要事先搭建环境模型。强化学习不需要环境模型,它的学习方式是不断的进行试错。在路径规划中,移动机器人学会了如何制定一系列动作来获得最大的回报[4-5]。近年来许多研究学者对强化学习在机器人路径规划上的应用进行了研究Ee Soong Low等人用FPA算法来改进Q-learning的初始化,加快了Q-learning的收敛速度[5]。徐哓苏等人将人工势场的引力势场引入到Q值初始化的过程中加快了收敛速度[6]。董瑶等人提出了基于竞争网络结构的改进深度双Q网络,使机器人到达目标点成功率得到了提高[8]。但是这些方法都没有解决连续动作空间的问题。用DDPG算法来规划机器人路径。针对DDPG算法在机器人路径规划上存在收敛速度慢等问题,对DDPG算法做如下改进:(1)引入改进的人工势场,加快DDPG算法的收敛速度和机器人到达目标点的速度。(2)根据移动机器人运动的实际情况,增加了直走奖励,避免机器人陷入局部最优。

1 基于深度强化学习的移动机器人路径规划框架

1.1 移动机器人模型

Pioneer3移动机器人的模型如图(1)所示,后驱轮和前驱轮是该机器人的主要组成部分,后驱轮的速度为v,q(x,y,θ)表示移动机器人位姿,(x,y)为后轴点的参考点,θ为移动机器人坐标位置和空间坐标位置的夹角,φ为转向角;L1为前后轮的轴距。

移动机器人运动学模型为:

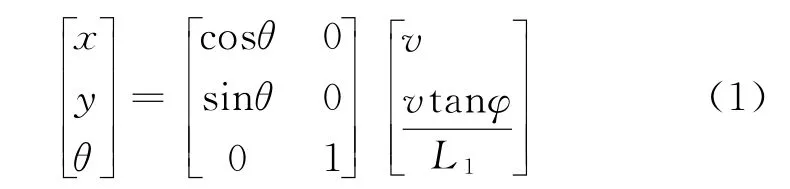
1.2 基于DDPG算法的路径规划策略

DDPG是TP Lillicrap等人在2016年对深度神经网络和DPG算法进行融合,并根据DPG算法和AC算法提出了一个无模型的强化学习算法[8]。DDPG算法做到了在连续空间选取动作的方法,而DQN算法只可以在离散动作空间选取动作。基于DDPG算法机器人路径规划框架图如图(2)所示。DDPG算法利用Actor网络产生路径规划策略,加入探索噪声后送入移动机器人进行执行。通过传感器获的当前状态信息s t,执行动作a,接着通过事先回报函数计算当前回报值。算法训练得到的经验轨迹(s t,a t,r t,s t+1)存入经验缓冲池里,进行随机抽取,这样可以避免时间的关联性和依赖性。然后利用梯度下降法对神经网络进行训练。DDPG算法的基本框架为Actor-Critic算法。在DDPG算法中,分别使用为θμ的策略网络来表示确定性动作选择策略a=μ(s|θμ),输入为当前状态s,输出确定性的动作值a;使用参数为θQ的价值网络来表示动作值函数Q(s,a|θq),用于求解贝尔曼方程。DDPG算法的目标函数被定义为折扣累积奖励的期望,表达式为:

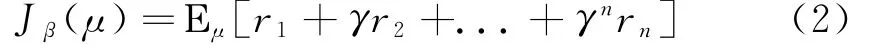
DDPG算法训练的目标是最大化目标函数Jβ(μ),同时最小化价值网络Q的损失。

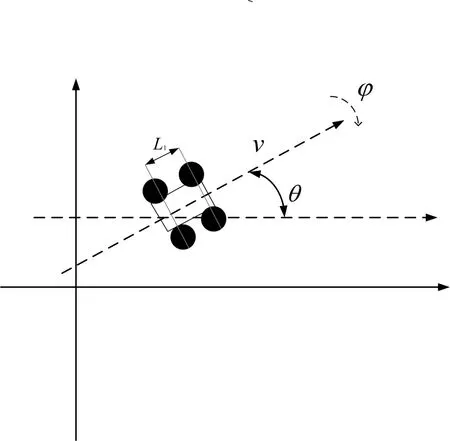
图1 移动机器人模型

图2 基于DDPG算法机器人路径规划框架

2 改进的移动机器人路径规划模型

2.1 人工势场和DDPG结合

DDPG算法规划的路径冗余且不平坦。而且DDPG算法在探索前期没有先验知识,只能随机的选择要执行的动作。当机器人面对复杂环境时收敛速度慢,易陷入局部迭代。基于以上问题引入人工势场的方法,以提高机器人前期的学习效率。使算法更快的收敛,加快机器人到达目标点的速度。

对于传统的人工势场来说,当目标点在障碍物附近,机器人向目标点移动的过程中,也会受到障碍物的影响。这样会导致机器人受到的吸引力减小,会造成目标不可达的现象。[10]所以使用改进后的人工势场。机器人在X=[x,y]T总势场值为:

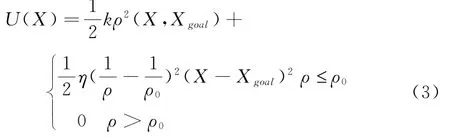
其中k为位置的增益系数,ρ(X,X g)是机器人当前位置与目标X goal之间的距离。

η为增益系数,ρ代表机器人与障碍物之间的最短距离,ρ0为障碍物的影响距离,通常为一个常数。

此时,势场中各状态的势场值代表状态s i的最大累积回报V(s i)。

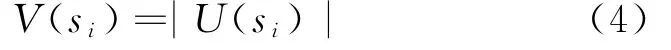
根据式(5)来跟新状态值函数Q值:

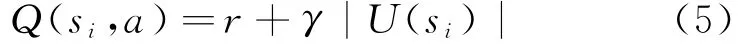
2.2 奖赏函数的改进

利用单步跟新的方式定义避障上的奖赏函数。在移动机器人路径规划的场景中,强化学习的最终目标是使机器人的累积奖励值最大。奖赏函数决定了策略的好坏。所以增加直走奖励。避免机器人陷入局部最优。奖励函数定义如下:

d total代表总距离,d goal(s)代表机器人s时刻距离终点的距离。

2.3 IAPF-DDPG路径规划方法

基于IAPF-DDPG的移动机器人路径规划方法如下:

Step1:建立以目标点为势场中心的重力势场;

Step2;根据等式(6)计算最大累积回报;

Step3:机器人从起点探索环境,选择当前状态s i下的动作。环境状态更新到s0,并且返回回报值r,并根据(6)更新奖励值;

Step4:根据新定义的等式(5)状态值函数更新Q值,随后更新Critic网络;

Step5:观察机器人是否到达目标点或到达设定的最大学习次数。如果两者遇到其中一个,学习回合结束。否则,返回到Step3

3 实验验证分析

为了验证提出的改进DDPG算法在路径规划中的收敛速度和路径平滑度上优异性,利用栅格地图对提出的改进方法与DDPG算法及其他相关改进方法做了效果对比。在仿真实验中对DQN(Deep Q Network),DDPG以及基于IAPFDDPG算法进行对比和实验分析。三种比较方法设置相同的神经网络机构和网络参数。算法中涉及到的参数设置如下:学习率α=0.5,折扣因子γ=0.9,经验池大小设置为2000。人工势场参数设置如下:k=1.6,η=1.2,ρ0=3.0。

在以上参数设置下,进行路径规划实验。图3和图4中(a)～(c)分别对应算法DQN,DDPG,IAPF-DDPG的路径规划和算法收敛情况。图3对上述算法规划的路径进行了比较,可以看出DQN算法规划出的路径较冗余且不平滑,相对而言DDPG算法规划出的路径没有那么冗余但仍存在大量拐点。对比IAPF-DPG算法,在加入人工势场并对奖赏函数做出改进后,规划出的路径相对平滑,没有多余的冗余路径。

图3 三种算法路径规划

图4 算法收敛回合

提取了三种方法的实验数据,并从总迭代时间,最佳决策时间,碰撞次数等方面进行了比较,进一步说明了改进模型的有效性。如表1所示,基于离散空间的DQN算法在训练时间和收敛速度方面没有DDPG算法的效果好,DDPG算法和DQN算法相比,在找到最佳决策是时间上减少31%,与障碍物发生碰撞的次数减少43%。对比IAPFDDPG算法和DDPG算法可知,在DDPG算法中引入人工势场会使算法最佳决策时间减少16%,碰撞次数减少15%。从总转角可以看出,改进后的IAPF-DDPG算法规划出的路径较为平滑。与以上方法相比较,IAPF-DDPG算法具有较少的迭代时间和最佳决策时间。仿真结果表明,改进后的方法不仅在收敛率上得到了提高,降低了试错率。

表1 三种算法在路径规划中的性能比较

4 总 结

对于传统的路径规划算法来说,历史经验数据无法回收用于在线训练和学习,导致算法精度低,规划的实际路径不平滑,收敛速度慢。提出了一种改进的DDPG算法在路径规划上的应用方法。在算法前期引入人工势场,使算法的速度得到提高,同时也降低了试错率。为了避免机器人陷入局部最优,在奖励函数做了改进,增加了直走奖励。将改进后的DDPG算法和其他经典强化学习算法做了比较,实验结构表明,改进后的DDPG算法收敛速度快试错率低,而且可以实现连续运算输出,验证了该方法的有效性。只将改进后的算法在二维地图上进行了验证,没有考虑到实际的验证环境。机器人移动时复杂环境的运动模型和在真实环境中验证将是下一步研究的重点。