冶金生产工艺流程的数学建模及其应用研究

夏冰心

（甘肃工业职业技术学院，甘肃 天水 741025）

1 冶金生产工艺流程的数学模型设计

1.1 分析冶金生产工艺流程

选择冶金生产工艺中的湿法冶金技术，作为数学模型的研究对象，这种冶金技术是化学冶金的一种，其原理是金属及其化合物采用无机水或有机液体溶剂，从矿石中浸出、分离和提取。利用矿物的磁性差异进行选矿，在此基础上对矿石原料进行预处理、矿石浸取、固-液分离、溶液净化和富集分离、从溶液中提取金属或化合物、浸取渣和废液处理等单元操作过程[1]。以金属金为例，其湿法冶金工艺流程如图1所示。

图1 湿法冶金生产工艺流程图

在生产工艺流程中涉及的化学反应为：

为防止氰化物在反应过程中被水解，又为防止溶液中二氧化碳分解，减少铜、铁、砷、锑等硫化物对氧的消耗，常用石灰乳作保护碱，使溶液的pH值保持在区间[11,12]范围内[2]。

1.2 收集冶金生产工艺数据

为保证冶金生产工艺数学模型的应用性能，必须采集到足够数量的数据用来做辅助变量，从而分析出冶金生产工艺的运行规律。在冶金生产的多个设备上安装传感器设备，并通过对传感器上数据的实时读取，实现冶金生产工艺数据的收集。因为收集的辅助变量单元不一致，必须将辅助变量数据归一化为[-1,1]或[0,1]，进行规范化处理的主要目的是找到相同的标准。冶金生产工艺数据的归一化处理过程如下：

式中x为归一化前的数据，xmax和xmin是该样本的最小和最大值。

1.3 实现冶金生产工艺流程的数学模型建立

在冶金生产工艺数据的支持下，结合冶金生产工艺流程的分析结果，针对多个工序实现对数学模型的建立。

1.3.1 原料添加工序

根据物料平衡原理，利用公式3计算矿石原料的添加量。

式中[k]zd和[k]qd分别为元素k终点和起点，[k]为矿石中元素k的含量，参数Bk为元素k的收得率，另外W和计算结果WAK分别为金属或金属化合物重量和对应金属元素的矿石原料添加量。

1.3.2 浸出工序

将浸出金属元素的浸出率作为浸出工序的重要参数指标，该指标可直接反映浸出液中金属的含量。浸泡过程有两次，每次浸泡过程有五个浸泡槽，浸泡槽之间是串联的。因此，只需建立单个浸出槽的力学模型，就可以为每一个浸出槽建立力学模型。设置矿石平均粒径大小d、溶氧浓度Co、浸出体积V作为操作变量，按浸出率、液相金品位和NaCN添加量为预测目标，根据质量守恒方程和反应动力学方程，建立了浸出工序的动态模型。在冶金生产流程中浸出工序环节的溶解氧守恒与金属守恒模型可以表示为：

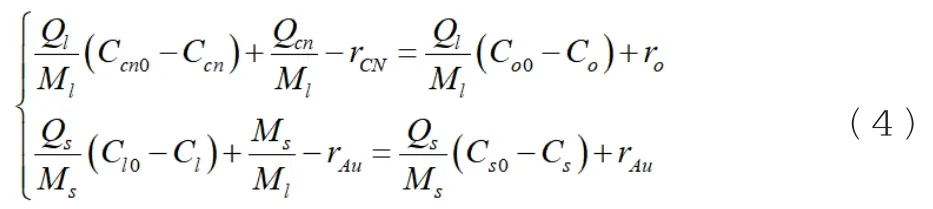
式中Ql、Qcn和Qs分别为矿浆中的水含量、氰化物添加量和矿石量，Ccn、Co、Cl、Cs分别对应的是液体中的氰根离子、溶氧、金属品位和液态金属品位的浓度。另外Ms、Ml表示的是浸出槽中滞留的矿石和液体质量，rCN、ro和rAu分别为氰化物、溶氧和金属的溶解反应速率。那么氰化浸出的过程，可以得出浸出槽中的金浓度和氰离子浓度微分方程为：

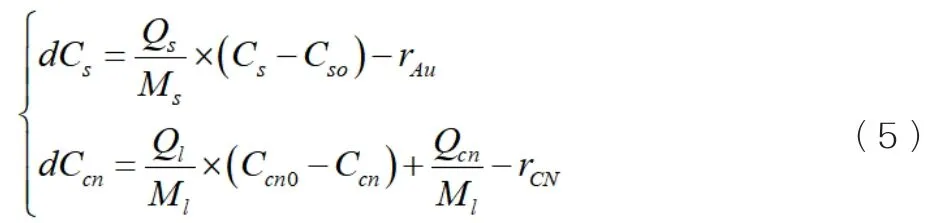
通过建立单个浸出槽的机理模型，利用浸出槽之间的串联关系，可以得到多阶段浸出的机理模型。

1.3.3 压滤置换工序

板框式压滤机对置换过程进行了模拟，并与板框式压滤机相结合建立了整个置换过程的动力学模型。假设压滤机工作在一定压力下，结合物料的守恒方程和反应动力学方程，即可建立模型如公式6所示。

式中F0表示的是流入压滤机的贵液流量，CA0和CA分别为金属氰离子和贫液中金属氰离子的浓度。

1.3.4 冶金生产工艺能量变化

冶炼生产过程中能量的变化分为三个部分：能量消耗、能量损耗、能量收益，其中能量收益包括矿石加热、熔化、过热和吸热反应所消耗的热量，而能量损失是生产设备表面散热和辐射散热，而收益是矿石物理散热，通过吹氧产生的化学反应热等等。以消耗能量中的矿石加热所需的热量为例，其表达式为：

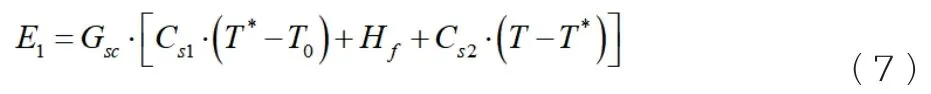
其中GSC为矿石配入量，CS1和CS2分别为固态、液态平均热容，T＊、T0、和T分别为矿石的熔点、初始温度和终点温度，Hf表示的是矿石的熔化潜热。

2 应用实验分析

为检验数学建模在冶金生产工艺流程中的应用效果，将该模型应用于实际冶金生产工作中，并在应用模型前后进行了对比。试验开始前，首先建立数学模型的运行环境，即METSIM软件。该软件是一个多功能的工艺过程模拟系统，能实现设备类型和生产规模的任意变化，并提供工艺评估平台。在冶金施工环境中，将实际的冶金项目数据输入到METSIM软件中，并利用相关的硬件设备收集生产工艺流程中产生的实时数据，以此作为量化的应用性能测试结果。为了凸显设计数学模型的应用性能，设置两个实验对比项，分别为未使用数学模型的冶金生产结果和应用传统建模方法的冶金生产结果，在实验过程中保证初始矿石原料和使用的冶金生产工艺相同，保证实验变量的唯一性。初始冶金的原料配入量设置情况，如表1所示。

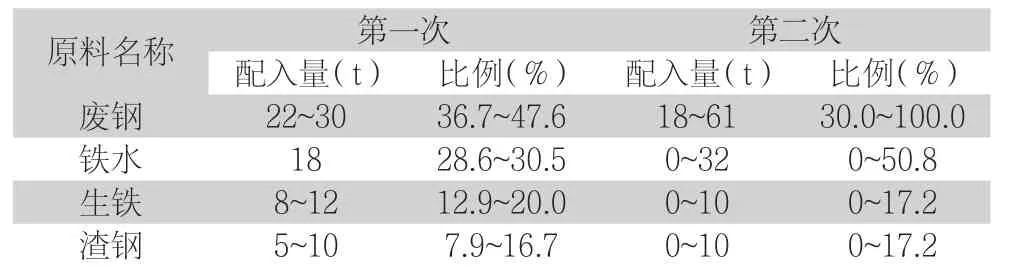
表1 冶金生产初始原料设置表

实验分别从冶金质量和成本消耗两个方面进行应用性能检测，其中冶金质量的测试指标为杂质含量，杂质含量越高证明冶金质量越差。另外成本消耗主要指的是冶金过程中的能量消耗，能量消耗越多证明成本越大，即应用性能越差。通过相关数据的统计与对比，得出实验结果如表2所示。

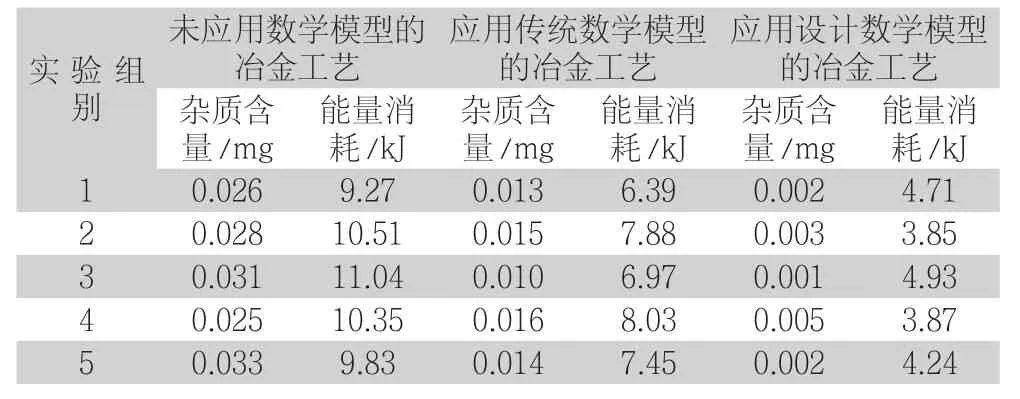
表2 应用性能测试结果

从表2中可以看出，为应用数学模型的冶金工艺的平均杂质含量和能量消耗分别为0.0286mg和10.2kJ。应用传统数学模型和设计数学模型的平均杂质含量分别为0.0136mg和0.0026mg，另外两种情况下的平均能耗分别为7.344kJ和4.320kJ。综上所述，将设计的数学模型应用到实际的冶金生产工艺流程中，具有良好的应用效果。

3 结语

由于金属种类繁多，熔炼工艺复杂，生产流程长，反应机理复杂，相互耦合严重，这给有色冶金过程的建模和优化带来了很大的困难，尤其是金属矿源复杂，工艺特殊，而国外引进的数学模型和优化软件也很难适应我国熔炼工艺的特点，严重制约了我国有色金属冶炼生产的发展。根据冶金过程控制的工程实践建立数学模型，并结合国家节能降耗和减排的重大战略需求，进行模型优化。利用数学模型的设计和应用，创造条件，突破资源、能源、环境对工业发展的限制，推动工业自动化的发展。