基于数据挖掘的光通信系统信息传输误差预测研究

于继江， 董中平

(中国食品药品检定研究院， 北京 102629)

0 引言

随着通信技术、光传感技术的不断发展，产生了光通信系统，相对于其他通信系统，光通信系统的信息传输速度快、对环境要求比较低，在许多领域得到了广泛的应用[1-3]。在光通信系统的实际应用过程中，影响光通信系统性能的因素比较多，如大气湍流、光反射等，使得光通信系统数据传输不稳定，传输成功率比较低，难以满足光通信系统的实际应用要求[4]。信息传输误差预测可以了解光通信系统变化特点，根据预测结果制定一定相应的措施，并进行技术改进，因此光通信系统信息传输误差预测成为了人们关注的焦点[5]。

针对光通信系统信息传输误差预测问题，许多学者进行了深入的研究，当前存在许多有效的光通信系统信息传输误差预测模型[5]。光通信系统信息传输误差预测模型大致可以划分为两类[6-8]：一类是传统模型，主要为线性回归方法、灰色理论，它们的光通信系统信息传输误差预测建模过程比较简单，由于传统模型假设光通信系统信息传输误差是一种线性的变化规律，但现代光通信系统信息传输误差具有一定的时变性，传统模型的预测偏差比较大，实际应用价值比较低；另一类为现代模型，主要以神经网络为代表的光通信系统信息传输误差预测模型，它们可以描述光通信系统信息传输误差的时变性，因此光通信系统信息传输误差预测效果得到了明显的改善。但在实际应用中，神经网络也具有一定的不足，如学习速度慢，建模过程复杂，因此对光通信系统信息传输误差预测结果有时不可太靠[9]。

由于信息传输误差预测对光通信系统影响十分重要，为提升光通信信息传输的成功率，提出了基于数据挖掘的光通信系统信息传输误差预测模型。首先分析影响光通信系统信息传输的影响因素，然后引入数据挖掘技术对影响因素和光通信系统信息传输误差之间的变化关系进行建模与分析，最后通过具体的仿真实验验证了本文光通信系统信息传输误差预测模型的有效性和优越性。

1 数据挖掘的光通信系统信息传输误差预测模型

1.1 影响因素分析

1.1.1 大气湍流

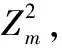
(1)

(2)

Δsr=sr(d4 d-1)

(3)

式中，β、sec(φ)分别表示波长和偏角；d表示垂直坐标；sr表示无湍流时的光功率。

1.1.2 背景光模型

光通信系统进行信息传输时，通常采用两级跟踪探测器，它们分别为粗跟踪探测器和精跟踪探测器，设sms、sg分别为信噪比和斜率系数；μbeam为光斑的直径，那么探测器的等效噪音角U计算式具体如式(4)—式(6)。

(4)

sms=4.14/μbeam

(5)

sg=1.27/μbeam

(6)

粗跟踪通常情况下采用CCD探测器，其信噪比具体为式(7)。

(7)

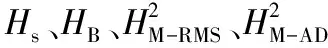
精跟踪通常情况下采用四象限探测器，其信噪比具体为式(8)。

(8)

式中，DEA表示背景光强度；p表示普朗克常数。

背景光谱密度为φ(λ)，光通信系统信息接收的口径和视场角分别为e和α，光通信带宽为Δf，它们之间存在的关联性Γ为式(9)。

(9)

1.2 设计光通信系统的信息传输误差预测模型

在光通信系统信息传输误差建模过程中，就是找到一种模型，该模型可以准确描述影响因素大气湍流、背景光与光通信系统信息传输误差之间的变化关系，从而提高光通信系统信息传输质量。相对于人工神经网络，数据挖掘技术中的支持向量机采用结构风险最小化原则进行建模，其建模精度要高于人工神经网络，而且预测结果更加可靠。对于样本集合{xi}∈Rn,i=1,…,l，其中l表示样本的数量，那么支持向量机建模实际就是通过寻找一个最优超平面将它们分开[11]，支持向量机的最优超平面如图1所示。

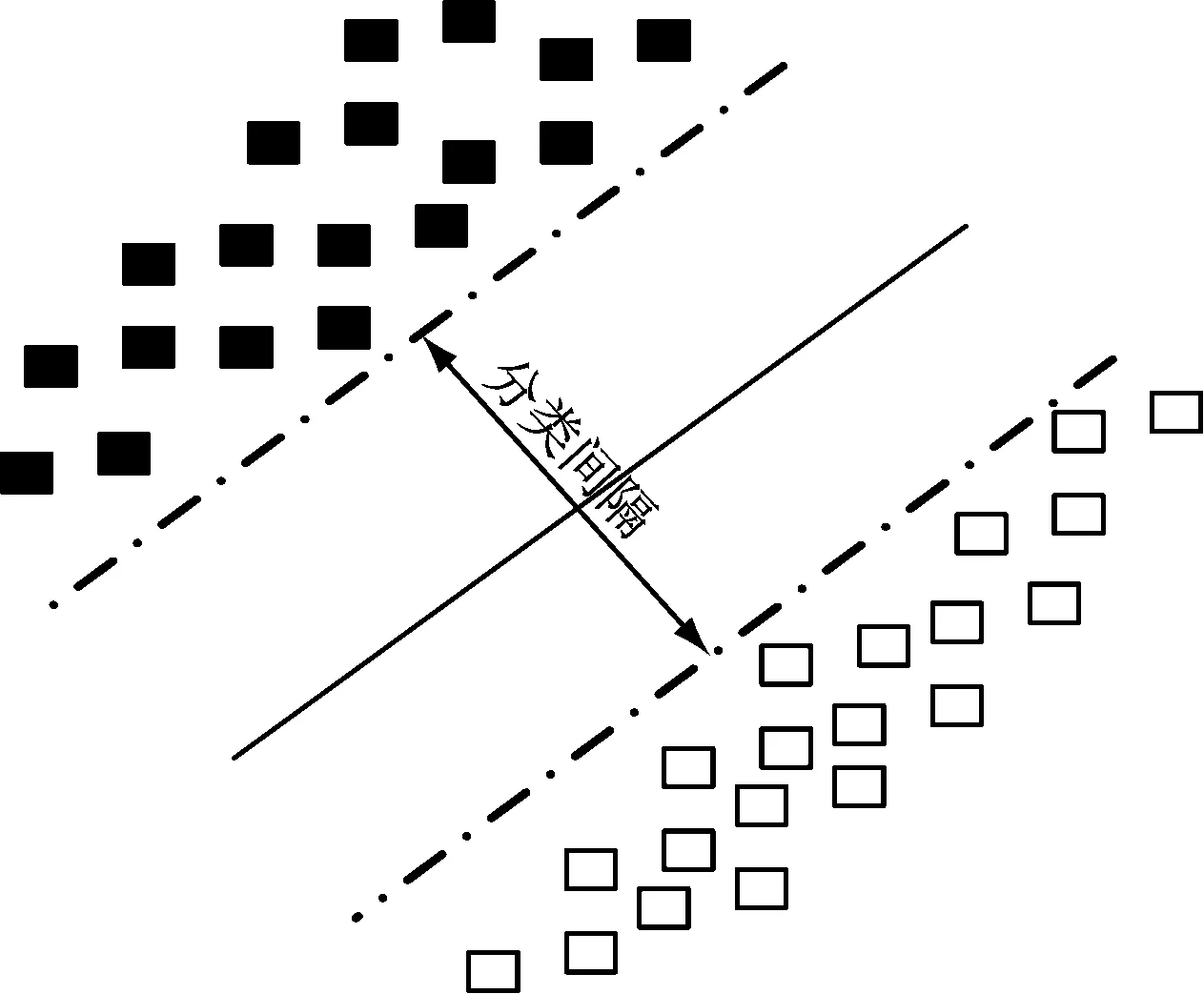
图1 支持向量机的最优超平面

最优超平面描述为式(10)。

ω·x+b=0

(10)

式中，·为点积操作；ω为n维向量；b为最优超平面的偏移量。

对于每一个数据点，尽可能使其与最优超平面之间的距离最大，这样可以得到一个与式(10)等效的二次优化问题，具体描述为式(11)。

(11)

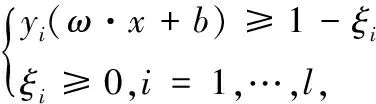
式中，ξ=(ξi,…,ξl)T表示松弛因子；C表示惩罚参数。

为了加快问题的求解效率，对式(11)进行转换，得到其对偶形式，具体如式(12)。

s.t.

(12)

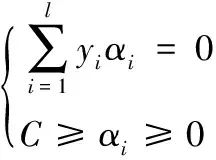
式中，α表示Lagrange乘子，其应该满足式(13)。

αi[yi(ω·x+b)-1]=0

(13)

得到支持向量机的决策函数为式(14)。

(14)

对于光通信系统数据，由于光通信系统信息具有非线性变化特点，支持向量机引入核函数对其进行转换，把非线性变化数据的空间转换成线性变化数据的空间[12]，具体如图2所示。

(a) 原始数据分布

对于光通信系统的信息传输误差预测问题，由于引入了核函数，式(12)的对偶形式变为式(15)。

s.t.

(15)

式中，K(xi·xj)表示核函数，具体定义如式(16)。

(16)

式中，σ表示核宽度参数。

2 仿真测试

2.1 测试环境

为了测试基于数据挖掘的光通信系统信息传输误差预测效果，采集一段时间的光通信系统信息作为实验对象，采用MATLAB工具箱搭建光通信系统信息传输误差预测的测试平台。

2.2 大气湍流对光通信系统性能影响的测试

在不同大气湍流条件下，测试其对光通信系统性能的影响，具体如图3所示。

图3 大气湍流对信息传输误差影响程度

对图3的信息传输误差进行分析可以发现，随着大气湍流的值不断增加，信息传输误差呈上升趋势，因此在实际应用中尽可能使大气湍流强度越小，以获得理想的光通信系统信息传输效果。

2.3 背景光对光通信系统性能影响的测试

在不同背景光条件下，测试其对光通信系统性能的影响，具体描述如图4所示。

图4 背景光对信息传输误差影响程度

对图4的信息传输误差进行分析可以发现，随着背景光值不断增加，信息传输误差同样呈上升趋势，但是其影响程度不如大气湍流，这表明本文选择背景光、大气湍流两种影响因素对光通信系统信息传输误差进行建模的思想是正确、有效的。

2.4 光通信系统信息传输误差预测效果分析

为了进一步验证数据挖掘的光通信系统信息传输误差预测的优越性，选择BP神经网络的光通信系统信息传输误差预测模型(BPNN)、多元线性回归的光通信系统信息传输误差预测模型(MLR)在相同实验环境下进行对比测试，选择光通信系统信息传输误差预测精度作为评价指标，预测精度计算式具体为式(17)。

(17)

式中，Tvalue和Pvalue分别表示实际传输误差与预测误差。

每一种模型均进行5次光通信系统信息传输误差预测建模，统计每一次预测精度，得到结果如表1所示。

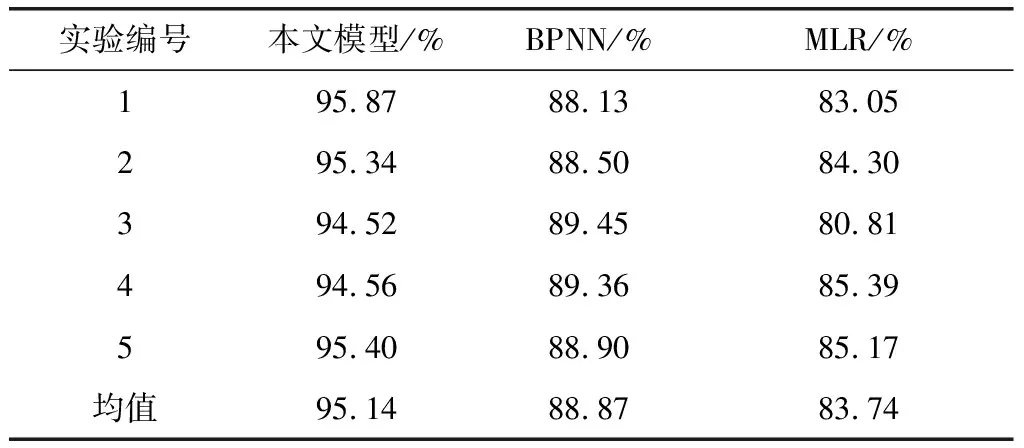
表1 光通信系统信息传输误差预测精度对比

对表1的光通信系统信息传输误差预测精度进行分析可以发现，本文模型的光通信系统信息传输误差预测精度均值为95.13%，而BPNN和MLR的光通信系统信息传输误差预测均值分别为88.87%和83.74%，由此可见本文模型降低了光通信系统信息传输预测误差，可以改善光通信系统信息传输效果，具有十分明显的优越性。

3 总结

针对当前光通信系统信息传输误差预测建模过程中存

在的一些难题，结合光通信系统信息的变化特点，以提高光通信系统信息传输误差预测精度，提出了基于数据挖掘的光通信系统信息传输误差预测模型，选择大气湍流、背景光作为影响因素，将它们作为支持向量机的输入，信息传输误差作为支持向量机的输出，通过支持向量机进行训练和学习，对输入和输出之间的关系进行拟合，测试结果表明，大气湍流对光通信系统信息传输效果的影响程度要高于背景光，对照实验证明了本文模型的光通信系统信息传输误差预测精度要明显优于当前其他模型，可以提升光通信系统信息传输质量，具有十分广泛的应用价值。