函数解析式求法“大集合”

■王佩其

函数的解析式是表示对应关系的代数式,是函数三种表示法中最重要的一种,对某些函数问题,能否顺利解答,往往取决于是不是能够求出函数的解析式。那么确定函数解析式有哪些基本方法呢?

一、待定系数法

当已知f(x)的结构时,可设出含参数的表达式,再将已知条件转化为方程或方程组,进而求出有关参数的值,即得函数f(x)的解析式。

例1(1)已知函数f(x)为一次函数,且满足f[f(x)]=4x-3,求函数f(x)的表达式。

(2)已知二次函数f(x)满足f(0)=1,f(1)=2,f(2)=5,求函数f(x)的解析式。

评析:待定系数法求函数的解析式的关键是列方程组,这种方法充分体现了方程思想的应用。

二、配凑法

已知f[g(x)]=h(x),求f(x)的解析式,可先用g(x)表示h(x),然后再将g(x)用x代替,即得f(x)的解析式。

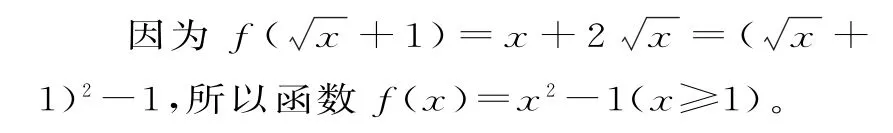
评析:配凑法的本质是一种整体代换的思想,这里“整体”的取值范围就是函数的定义域,即题中+1≥1。

三、换元法

已知f[g(x)]=h(x),求f(x)的解析式,若用配凑法不容易求出时,可设g(x)=t,从中解出x,代入h(x)进行换元求解。

评析:利用换元法求解析式,一定要注意“新元”的取值范围,即函数的定义域。

四、构造法

已知关于f(x)与或f(-x)的表达式,可根据已知条件再构造出另外一个等式,然后通过解方程组求出f(x)的解析式。

例4已知函数f(x)满足f(x)+2f(-x)=x3-2,求函数f(x)的解析式。

解:以-x代替f(x)+2f(-x)=x3-2中的x,可得f(-x)+2f(x)=-x3-2。

评析:对于函数f(x),当满足形如af(x)+bf(-x)=g(x)(a≠b≠0)或af(x)+bf=g(x)(a≠b≠0)关系时,可用-x或代替关系式中的x,得到的新关系式与原关系式联立消元,即得函数f(x)的解析式。

五、根据实际问题求解析式

函数在现实生活中有着广泛的应用,其解析式“隐藏”在实际问题中,可以根据实际问题来求函数的解析式。

例5为了尽快改善职工住房困难,鼓励个人购房和积累建房基金,决定住房的职工必须按基本工资的高低交纳住房公积金,办法如表1所示。

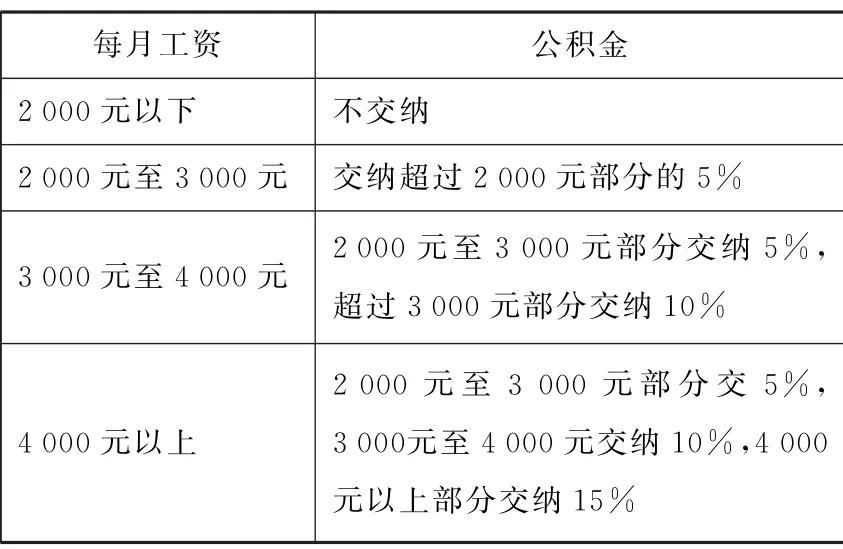
表1

设职工每月工资为x元,交纳公积金后实得工资为y元,求y与x之间的关系式。

解:由题中的表1可知,当0

由上可得y与x的关系可用分段函数表示为y=

评析:根据实际问题求解析式,必须先读懂题意,再将题中的“自然语言”转化为“数学语言”,然后求出解析式,但需要注明函数的定义域。

六、利用函数的性质求解析式

函数具有单调性,奇偶性,周期性等性质,这些性质同时反映在它们的图像上,因此利用图像特征是求函数解析式的有效途径之一。

例6若奇函数f(x)的定义域为R,且当x>0 时,f(x)=,试求函数f(x)的解析式。

评析:题中函数f(x)是一个定义域为R的奇函数,所以f(0)=0。这类问题的最终结果一般是一个分段函数。

感悟与提高

甲同学家到乙同学家的途中有一公园,甲从家到公园的距离与乙从家到公园的距离都是2km,甲10 时出发前往乙家。图1 表示甲从出发到乙家为止经过的路程y(单位:km)与时间x(单位:min)的关系。试写出y=f(x)的函数解析式。