随机删失单函数型指标模型条件众数估计的渐近正态性
丁海玲, 凌能祥
(合肥工业大学 数学学院,合肥230601)
1 引 言
在非参数统计推断中,探索响应变量和解释变量之间的关系时,条件密度占据重要地位.关于条件密度和条件众数的研究一直是令人十分感兴趣的内容.随着信息化时代的发展,越来越多的领域所获取的数据呈现出函数特征,函数型数据的研究也逐渐成为热门.在实际生活中,得到的数据往往形式各异、类型复杂,所以现在的数据研究类型已不满足于完全独立观测数据,而更倾向于相互依存的随机删失和随机缺失数据,这样的研究结果更具有实用性也更有意义.
Ferraty和Vieu[1]基于函数型数据的非参数统计方法,获得了样本在独立和α-混合条件下条件密度估计的几乎完全收敛速度.Ezzahriouia和Ould-Said[2-3]在样本独立情况下分别获得了条件分位数和条件众数的渐近正态分布.Attaoui等[4]研究了基于样本在独立场合下单函数型指标模型条件密度的非参数双重核估计,并获得了几乎完全一致收敛速度.此外,Ling等[5-6]利用Kolmogorov-ε熵的方法,研究了单函数型指标模型的条件密度估计,获得了样本在α-混合情况下条件密度估计及条件众数估计的几乎完全一致收敛速度.Attaoui和Ling[7]研究了单函数型指标模型时间序列数据的条件累积分布估计的渐进结果.Ling等[8]研究了遍历数据在响应变量随机缺失条件下的条件众数估计,获得条件众数估计的收敛速度和渐近正态性.吴波[9]基于遍历函数型数据,研究了条件风险率函数的核估计.Ling等[10]研究了遍历数据在响应变量随机删失的核回归估计.Benkhaled等[11]利用局部线性估计方法,获得随机删失条件下条件密度的强一致性.针对α-混合时间序列数据,本文基于单函数型指标模型,主要研究在响应变量Y随机删失时条件密度和条件众数的渐近正态分布.
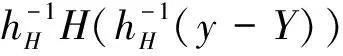
2 模型与假设
2.1 模型及相关标记
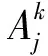
则称{Xn,n≥1}是α-混合的随机变量序列.假定(Xi,Zi,δi)1≤i≤n是来自总体(X,Y,δ)的数据样本.基于数据集(Xi,Zi,δi)1≤i≤n,本文构造密度函数f(θ,y,x)的估计如下:
其中
这里K和H是核函数,hK=hK,n>0和hH=hH,n>0是正向的序列光滑参数,并且当n→∞的时候趋于零.
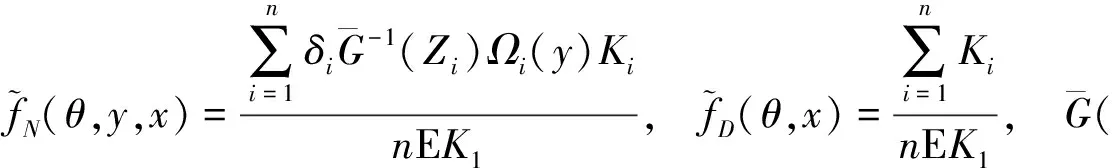
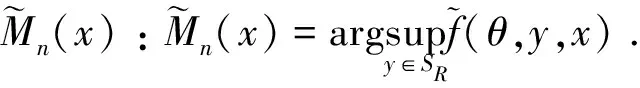

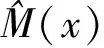
2.2 假设条件
本文中出现的C是不依赖于n的正实数,下面给出一些必要的条件:
(A1) 存在一个可导的函数φ(·),使得对任意x∈SH,θ∈ΘH有
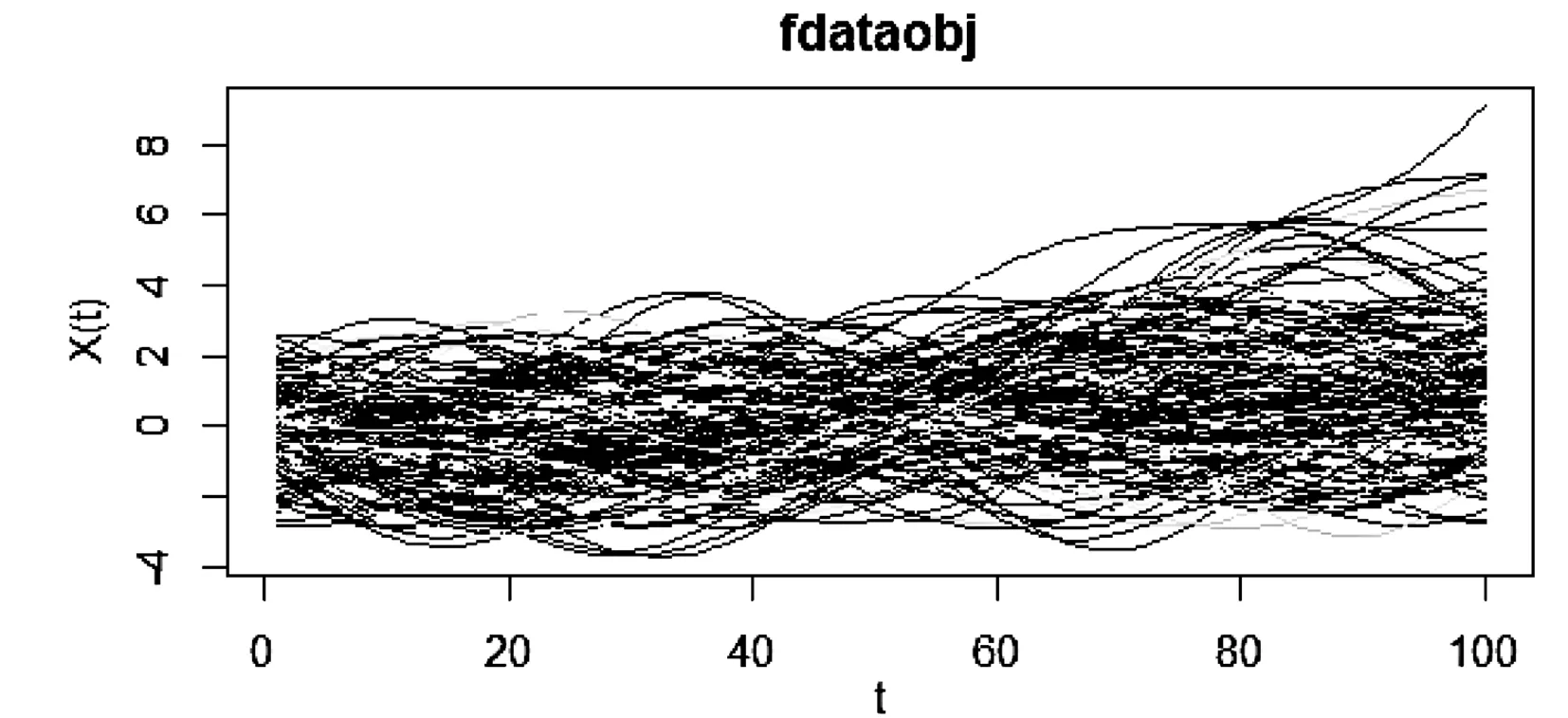
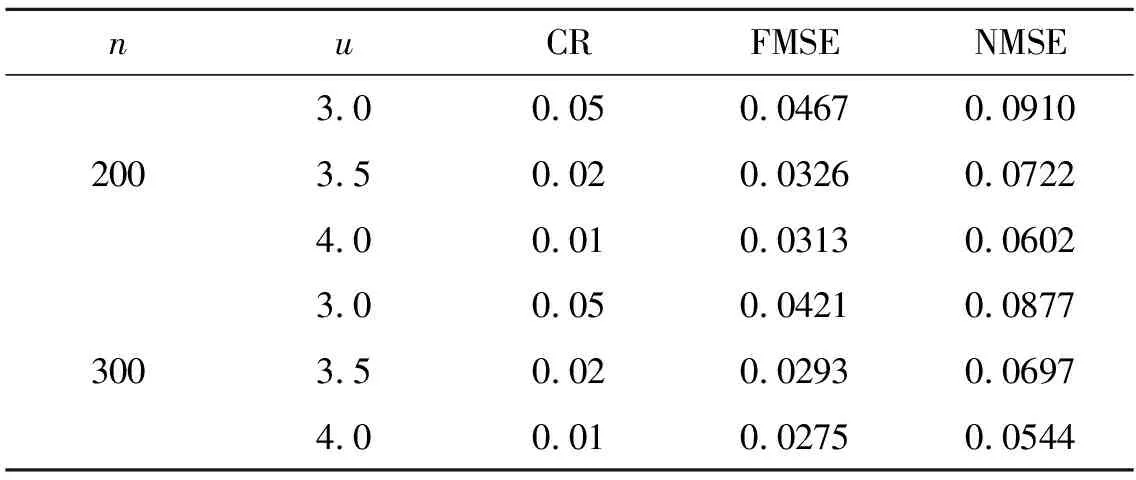
0 且当hK→0时,φθ,x(hK)→0; (A2)K在支撑集[0,1]上非负有界且在[0,1]上可微,存在正实数c1,c2,使得 -∞ (A3)H是非负有界函数,满足 (A4) 条件密度f(θ,y,x)满足 (i) 存在β1>0,β2>0,对任意(x1,x2)∈SH×SH, (y1,y2)∈SR×SR,θ∈ΘH有 |f(θ,y1,x1)-f(θ,y2,x2)|≤c(‖x1-x2‖β1+|y1-y2|β2), (ii) 存在β0>0, (y1,y2)∈SR×SR,对任意q=1,2有 |f(q)(θ,y1,x)-f(q)(θ,y2,x)|≤c(|y1-y2|β0), (iii)f(θ,·,x)在M(x)处二阶连续可微,且|f(2)(θ,M(x),x)|≠0,其中f(q)(θ,y,x),q=1,2表示f(θ,y,x)关于y为q阶可导, (iv) 存在ζ>0和唯一的y0∈SR,使得f(θ,·,x)在(y0-ζ,y0)上严格递增,在(y0,y0+ζ)上严格递减; (A5) (Xi,Yi)i∈N满足 (ii) 存在βθ,x(·),使得对任意t∈[0,1],都有 (A6) 算术α-混合中的a>3,窗宽hK和hH以及小球概率φθ,x(hK)满足:当n→0时 (A8) 假设对任意ε>0,y∈SR,存在η>0,使得:|M(x)-y|≥ε,则有 |f(θ,M(x),x)-f(θ,y,x)|≥η. 注 (A1)-(A4)是单函数型指标模型中条件密度和条件众数的基本假设,文献[4]有类似假设.(A5)给出了联合分布(xi,xj)相对于其边缘的性质,并允许我们给出一个显式渐进方差项.(A6)-(A7)给出小球概率和窗宽的条件,以及α-混合的相关条件和性质.(A8)是对条件众数的基本假设. 定理1条件(A1)-(A7)成立时,有 其中 由于上述结果不能直接应用于实际,对未知函数做估计 由估计值则可以得出 定理2在定理1成立的条件和条件(A8)下,有 其中 证明之前,先做如下分解: 下面给出必要的三个引理以及相关证明. 对于J1: 由(A1),(A2)可知 所以 对于J2: 这里an=o(n)为特定选择.首先对于J2,1,由条件(A1),(A2),(A6)有 所以 即 可知 选取合适的an,使得当n→∞时,J2,1→0.对J2,2,运用强混合依赖的Davydov不等式[1],有 Cov{Ki,Kj}≤C{E(Ki)v}2/v[α(|i-j|)]1-2/v. 因为E|Ki|v=Cφθ,x(hK),所以Cov{Ki,Kj}≤C[φθ,x(hK)]2/v[α(|i-j|)]1-2/v.可知 即 引理2条件(A1)-(A4)成立时,当n→∞有 对任意度量函数φ(·),有 I{Y1≤C1}φ(Z1)=I{Y1≤C1}φ(Y1), 所以可得 引理2得证. 引理3条件(A1)-(A4),(A5)-(A8)成立,有 首先 第二步,由ηni的定义,对于i≠j,有 令 则 结合Licbscher[16]推论2.2得证. 接下来证明定理2,考虑到 由条件知 及f(2)(θ,y,x)的一致连续性,可得 由于 类似引理3的证明,即可得证.此时,定理2得证. 本节将展开单函数型指标模型条件众数估计在响应变量随机删失情况下的模拟研究,验证其估计的有效性.模拟方法及参数设置参考Ling等[10]和Ding等[18]关于删失和单指标的研究.文章构造函数型数据xi(t)为 图1 曲线xi(t), i=1,…,200. 其中 此外将比较条件众数的单函数型指标模型和函数型非参数模型的表现,函数型非参数模型为 Y=r(x)+ε. 在这里,曲线、核函数及窗宽的选取和单函数型指标模型相同,将采用如下半度量: 表1 不同模型在相同删失率下的MSE 从表1可以看到,在相同样本量的情况下,条件密度估计的预测效果(MSE)随着删失率CR的减小(u增大)而变好;删失率相同的情况下,样本量越大,预测精度越准,受缺失率的影响也越弱.在对删失数据的处理中,单函数型指标模型的表现要明显优于函数型非参数模型. 本文将单函数型指标模型和响应变量随机删失结合起来,并应用于α-混合的场合中,获得条件密度和条件众数估计量的渐近正态分布.模拟实验和真实数据分析也表明了模型的可行性和研究问题的实用价值. 致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.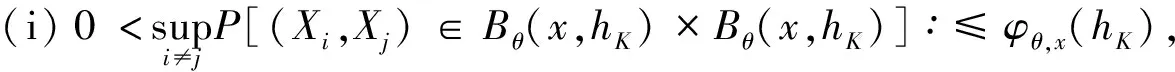
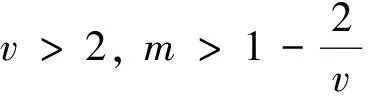
2.3 理论结果
3 引理及证明
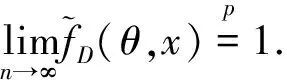
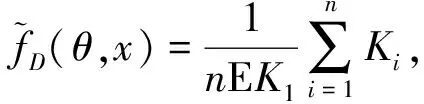
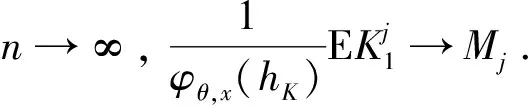

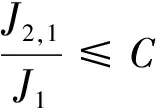
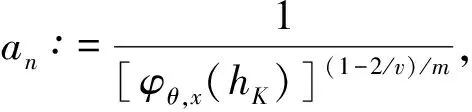
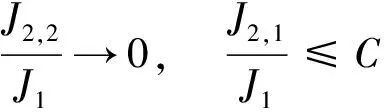
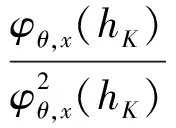
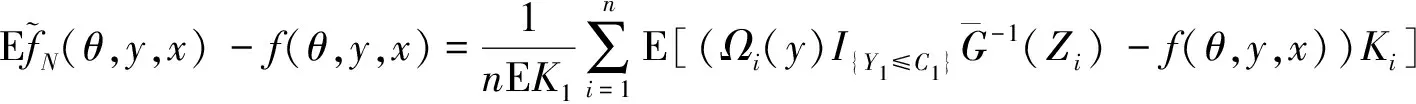
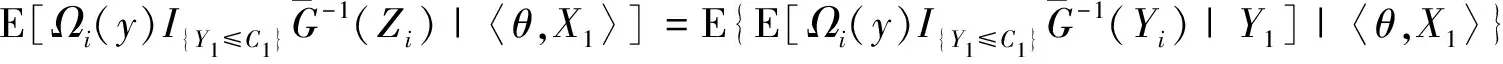

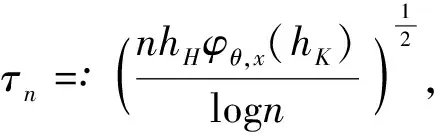
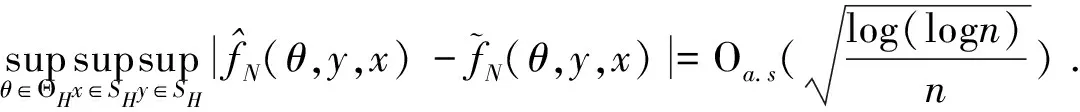
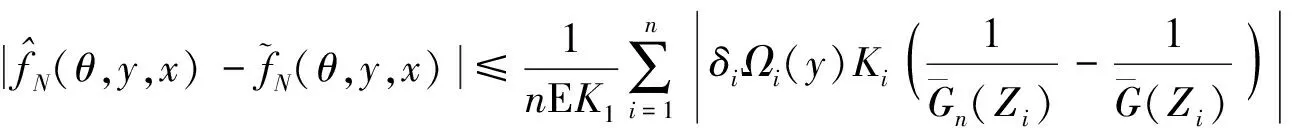
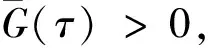
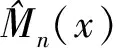
4 模拟研究
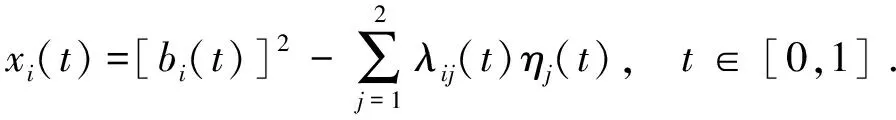
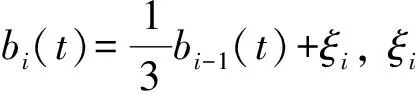
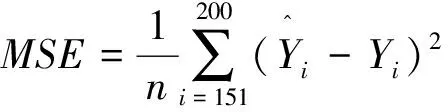
5 结 论

