平面双线性映射的伸缩率分析

李 倩， 王旭辉

(合肥工业大学 数学学院，合肥230601)

1 引 言

平面(2D)变形是图像处理中具有多种应用程序的操作，有着广泛的应用.例如，利用WarpGAN自动生成漫画[1].平面变形在3D几何参数化中也有着重要贡献[2].

经典的平面变形方法有Free-From变形(FFD)[3]、Thin-Plate样条(TPS)[4]和Mean-Value坐标(MVC)[5]，但它们并不能保证局部失真.因此，最近的平面变形强调控制局部失真，即保证角度的局部变形，为此引入了共形映射，可以最大程度地保留角度.因此，近年来共形映射及其近似被广泛用于平面变形[6-9]以及参数化[10-11].但共形映射的自由度少，且很难插入四个及以上的点并保证单射性.

在此基础上，研究者提出最小化共形失真，即构造最优拟共形映射.例如，Lipman等[12]提出了4点插值公式(FPI)，可以最小化最大共形失真且均匀分布在整个区域；Nian等[13]提出了一种基于交替方向乘法器(ADMM)迭代算法来计算Teichmüller映射，能产生更均匀的参数化，提高精度；Goswami等[14]在多边形之间提出一种基于O(1/ε4)的迭代算法来获得连续的极值拟共形映射，保证了伸缩商的减小；Weber等[15]基于Teichmüller对极值映射的全纯二次微分伸缩商的刻画，提出了一种计算零类曲面极值拟共形映射分段线性逼近的算法，具有良好的收敛性；Lui等[16]提出了拟共形迭代(QC迭代)算法来计算Teichmüller映射，其基本思想是用Beltrami系数(BCs)表示微分同胚集，寻找与Teichmüller映射相关的Beltrami系数(BC)，最后使用Linear Beltrami Solver(LBS)构造最优拟共形映射.

本文在平面区域内通过双线性映射[17]构造拟共形映射，针对平面凸四边形，研究双线性映射的伸缩率极值情况.

2 预备知识

本文考察双线性映射的伸缩率极值情况.令z=s+it是一个复变量，其中i2=-1,s,t∈分别是z的实部和虚部，记为z的共轭.对于任意可微复变函数f(z)，它将一个复平面映射到另一个复平面上，其导函数可被定义为

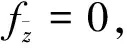
定义1(拟共形映射) 假设f∶D⊂→是复变函数，且具有连续偏导.若f满足Beltrami方程

(1)

且复值函数μf(z)满足‖μf(z)‖∞<1，则称f为拟共形映射.其中，μf(z)被称为f的Beltrami系数.

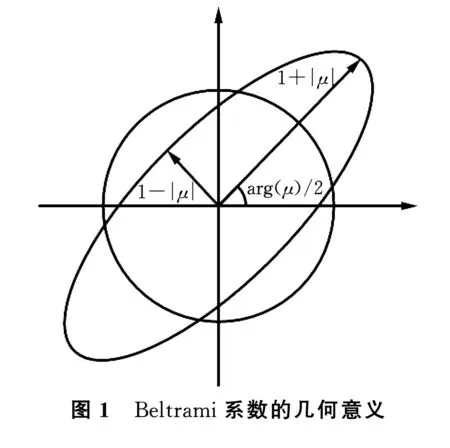
拟共形映射的Beltrami系数μf(z)可以用来衡量共形程度.拟共形映射是一种从微小圆到微小椭圆的映射，其中椭圆的离心率即f的伸缩商是由旋转角度arg(μf)/2的最大放大倍数1+|μf|和旋转角度(arg(μf)-π)/2的最大缩小倍数1-|μf|给出(见图1).因此，f(z)在z点处的伸缩商定义为

f的最大伸缩商定义为

由于当‖μf‖∈[0,1) 时，Kf关于‖μf‖成严格单调递增，故讨论伸缩商的最大值情况等价于讨论‖μf‖的最大值情况.下面分析双线性映射的伸缩商情况.

3 双线性映射

给定平面上一个凸四边形Q，其四个顶点分别为q00,q01,q10,q11∈2，且q00,q01,q10,q11为逆时针排序.将2上的向量(s,t)表示为复变量z=s+it的形式，则该四边形的顶点qij=(xij,yij),i,j=0,1，可表示为qij=xij+iyij.定义双线性映射如下：

F(z)=x(s,t)+iy(s,t)=q00(1-s)(1-t)+q01(1-s)t+q10s(1-t)+q11st，

(2)

其中(s,t)∈Ω=[0,1]×[0,1].该双线性映射为单位正方形区域映射到凸四边形区域Q上的一一映射.

由伸缩率函数的定义(1)，双线性映射F(z)的伸缩率函数μF可表示为

从而

(3)

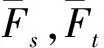
(4)

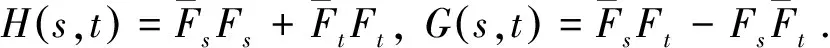
引理1设H(s,t),G(s,t),N(s,t),D(s,t)如公式(4)所定义，则有如下关系式

证由(4)得

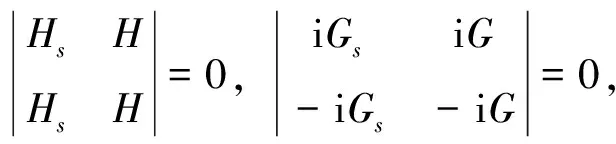
定理1双线性映射F(z)对应的γ(s,t)=|μF|2有且仅有一个驻点，且在该驻点处取极小值.

证首先记M⊂2是γ(s,t)的驻点集合，即

由引理1可得

所以

M={(s,t)|HGs-HsG=HGt-HtG=0,D≠0,s,t∈}.

由双线性映射的定义(2)知

deg(H)=2, deg(G)=deg(Hs)=deg(Ht)=1，

所以deg(HGs-HsG)=deg(HGt-HtG)=2，因此M中最多存在4组解.另外，由(4)可知

(5)

可得

(6)

根据双线性映射的定义(2)，可得

(7)

为了简化计算，将(7)记为

Fs=A0t+A1,Ft=A0s+A2,Fs t=A0，

(8)

其中A0=q00+q11-q01-q10,A1=q10-q00,A2=q01-q00.因此，(6)式的四个解可记为

又因为D=H-iG≠0，故只保留一组解，即

(9)

因此，γ(s,t)=|μF|2有且只有一个驻点，即双线性映射的伸缩率函数μF有且只有一个驻点.

再计算γ(s,t)的Hessian矩阵行列式值为

代入(4)，(5)，(8)式和驻点，可化简为

(10)

(11)

令A1=q10-q00,A2=q01-q00,A3=q11-q10，则A0=A3-A2.将A1,A2,A3记为

A1=ρ1eiθ1,A2=ρ2eiθ2,A3=ρ3eiθ3，

(12)

其中ρ0,ρ1,ρ2,ρ3是向量A0,A1,A2,A3的模长，θ1,θ2,θ3∈[0,π]为A1,A2,A3的辐角.则

(13)

(14)

从而，(11)式化为

故该驻点是极值点.又

所以在该驻点处取得极小值.

例1给定一个平面凸四边形Q1，其顶点分别为q00(0,0),q01(0,1),q10(2,0),q11(1,2)，则从Ω到Q1的双线性映射为

F(z)=2s(1-t)+i(1-s)t+(1+2i)st，

显然，Fs=2-(1-i)t,Ft=i-(1-i)s,Fs t=-1+i，其中A0=-1+i,A1=2,A2=i.

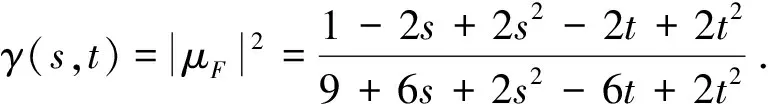
又因为

D=H-iG=9+12s+5s2-6t+5t2≠0，

定理2双线性映射F(z)的伸缩率函数μF的最大值发生在区域Ω的顶点处.

证若γ(s,t)=|μF|2最大值在区域Ω=[0,1]×[0,1]内部取得，由于γ(s,t)在除极点外充分光滑，那么γ(s,t)一定存在另一个驻点，使得最大值发生在Ω内部，与定理1矛盾.所以，γ(s,t)的最大值只能在边界上取得.下面考察γ(s,t)在边界s=0,s=1,t=0,t=1上的取值情形.由(4)和(8)式，可得

下面只考察γ(s,t)在s=0上的取值情况，其余三条边界类似.令

显然上式的分母在区间内[0,1]不为零.对T0(t)求导，可得

由于T0(t)的一阶导数的分母恒大于0，故只需讨论其分子.令g(t)为上式的分子部分，即

设g(t)=0，可得驻点

由(12)知

因此

又

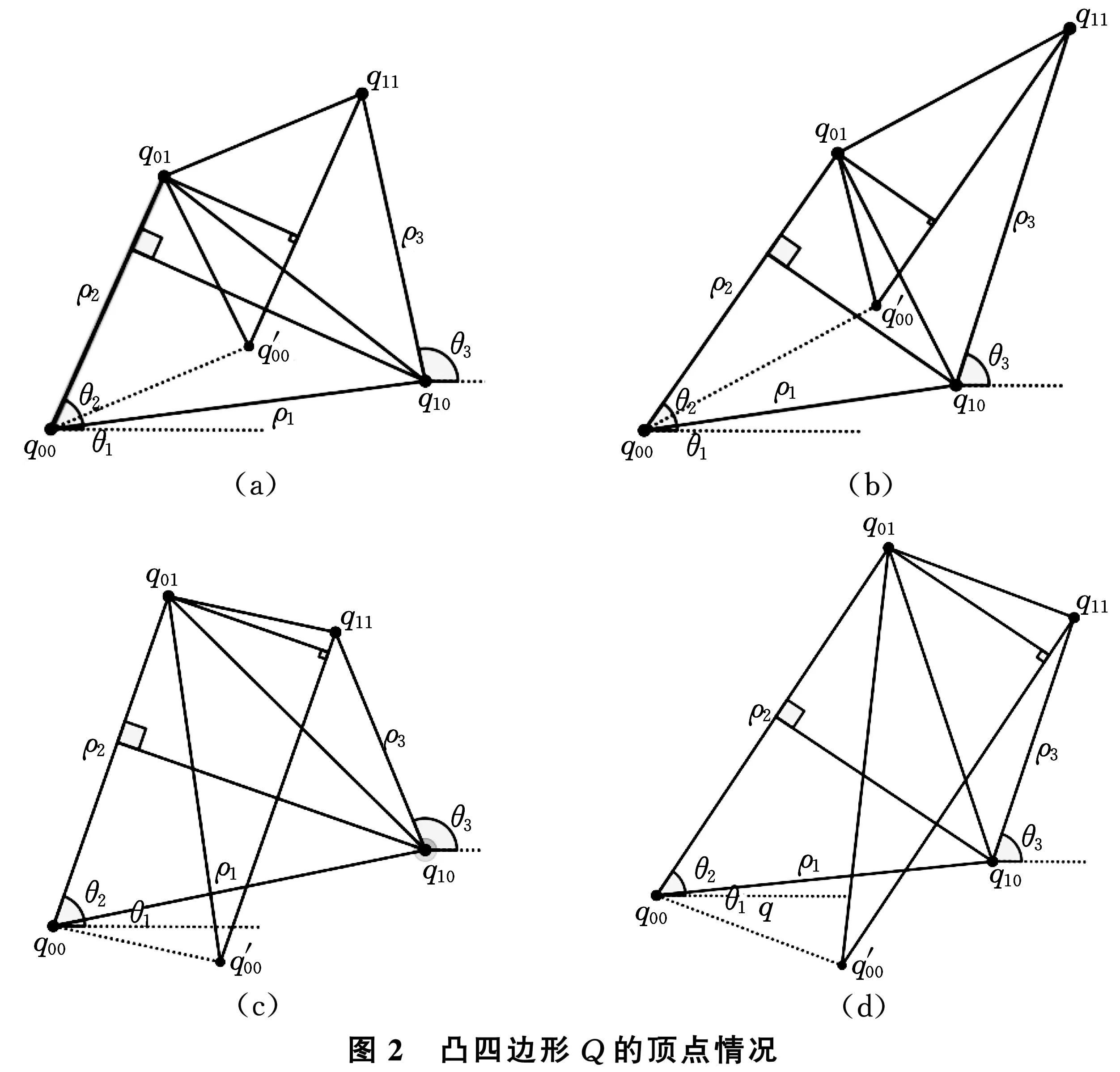
当θ3>θ2时且q′00位于四边形内部时，SΔq00q01q10>SΔq′00q01q10，即t>1(见图2(a)(b))；当θ3>θ2时且q′00位于四边形外部时，q′00的位置在q00与q10之间，仍有SΔq00q01q10>SΔq′00q01q10，即t>1(见图2(c)(d))；当θ3<θ2时，ρ2ρ3sin(θ3-θ2)<0，即t<0.

(i) 当θ3>θ2时，函数g(t)开口向下，对称轴t>1，那么在[0,1]间至多只有一个驻点t1.

若t1在[0,1]内，此时在[0,t1]上g(t)<0，在[t1,1]上g(t)>0，则T0(t)在[0,t1]上单调递减，[t1,1]上单调递增.又t1是驻点，取得极小值，故T0(t)的最大值在t=0或t=1处取得，即在顶点处取得最大值.

若t1不在[0,1]内，此时g(t)在[0,1]上恒大于0或者恒小于0，则T0(t)在[0,1]上单调.再考虑f(0)与f(1)的大小，有

故T0(t)在[0,1]上单调递增.又t1是驻点，取得极小值，故T0(t)的最大值在t=1处取得，即在顶点处取得最大值.

(ii) 当θ3≤θ2时，函数f(t)开口向上，对称轴t<0，那么在[0，1]间至多只有一个驻点t2.

若t2在[0,1]内，此时在[0,t2]上g(t)<0，在[t2,1]上g(t)>0，则T0(t)在[0,t2]上单调递减，[t2,1]上单调递增.又t2是驻点，取得极小值，故T0(t)的最大值在t=0或t=1处取得，即在顶点处取得最大值.

若t2不在[0,1]内，此时g(t)恒大于0或者恒小于0，,则T0(t)在[0,1]上单调.再考虑f(0)与f(1)的大小，有

所以T0(t)在[0,1]上单调递增.又t2是驻点，取得极小值，故T0(t)的最大值在t=1处取得，即在顶点处取得最大值.

故|μF|2的最大值发生在顶点处，即双线性映射的伸缩率函数μF的最大值发生在顶点处.

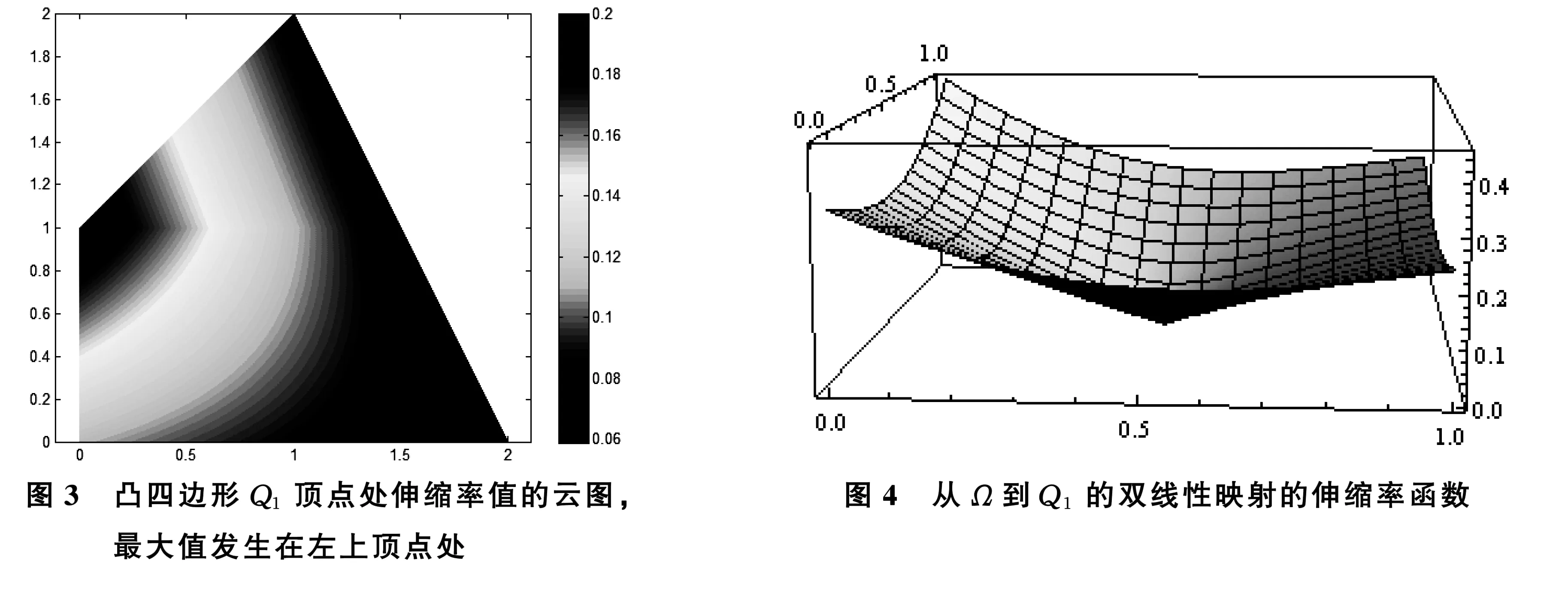
例2由例1，从单位正方形Ω到Q1的双线性映射为

F(z)=2s(1-t)+i(1-s)t+(1+2i)st，

其伸缩率函数为

则

可以得到伸缩率函数图像(见图4)，且清楚看出μQ1的最大值发生在顶点处.

例3给定一个平面凸四边形Q2，其顶点分别为q00(0,0),q01(0,3),q10(2,0)，q11(3,2).那么，从Ω到Q2的双线性映射为G(z)=2s(1-t)+3i(1-s)t+(3+2i)st，其伸缩率函数为

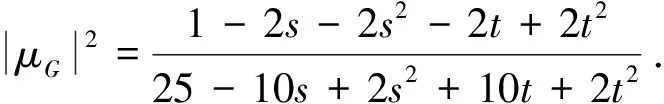
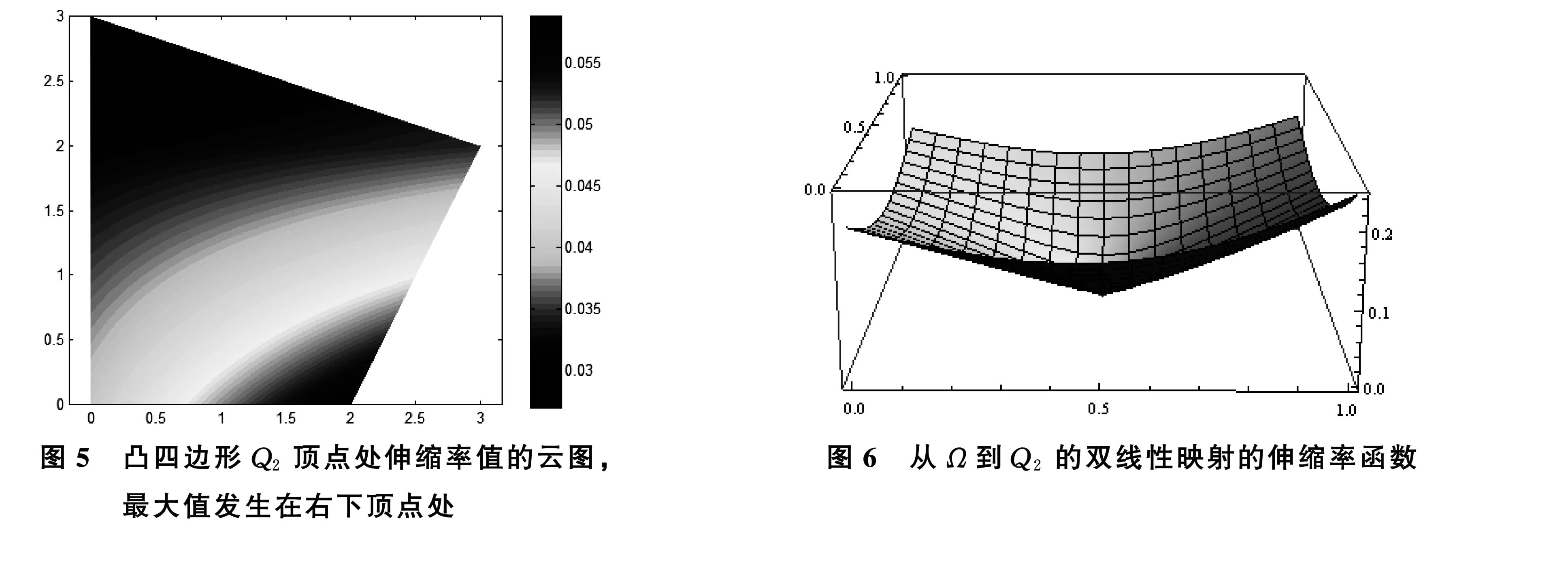
4 结 论

本文讨论了在平面区域上基于双线性函数的拟共形映射的最大值发生情况.首先定义单位正方形区域到凸四边形区域之间的双线性函数，然后在此基础上求出拟共形映射的伸缩率函数μF，最终通过定理1和定理2给出了拟共形映射的最大值发生在平面凸四边形的顶点处的结论.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.