基于BP-AUKF算法和FFRLS的蓄电池SOC估计

河海大学能源与电气学院 陈玉伟 顾钟凡 李承澳 张德春 黄 海

为满足当前电子产品应便于携带的要求，锂离子电池以其体积小、质量轻、充放电快等特点独占鳌头。同时随着传统能源的大量消耗和新能源的日益提倡，新能源电动汽车产业迅速崛起，带动了锂离子电池的深入发展，大容量锂离子电池已开始进入电动汽车等大功率设备的应用中，推动了新能源电动汽车行业的发展，所以锂离子电池和新能源电动汽车行业两者相互促进、发展迅速。目前在新能源电动汽车行业中主要应用的锂离子电池有磷酸铁锂电池、镍氢电池、电容电池、三元锂电池等。本文选取具有相对较高安全性的磷酸铁锂电池作为实验对象。

锂离子电池的荷电状态(SOC,State of Charge)就是日常所说电池剩余的容量，对电池的使用寿命、安全性和效率的评估具有非常重要的作用，准确的SOC 估算对于电池的高效利用和能量管理具有重要意义。可通过研究锂离子电池的电池模型来深入研究锂离子电池的SOC 状态估计，目前等效电路模型主要有RC 模型、PGNV 模型等。针对SOC 准确估计的问题，采用结构简单，却能同时反应电池外特性和内部电化学反应的二阶RC等效电路模型，这种模型便于进行电池特性分析和参数辨识。

目前有安时积分法、开路电压法、内阻法等常用的电池状态估计方法，本实验参数辨识实验中采用带遗忘因子的递推最小二乘法辨识模型参数（FFRLS，Forgetting Factor Recursive Least Squares），从而能够在大量实验数据中起到突出新数据的特点。在电池的SOC 估计环节中采用BPAUKF 算法，并通过实验验证此方法用于电池状态估计时的稳定性和精确度。

与传统的蓄电池SOC 估计方法相比，本文摒弃了传统的多项式拟合OSV-SOC 曲线，采用了较新的BP 神经网络算法[1]，在利用实验平台采集大量实验数据的前提下，有效提高了拟合精度。查阅相关资料可知，若噪声矩阵为统计特性已知的高斯白噪声时，则卡尔曼滤波具有较为准确的应用，然而当噪声矩阵具有不确定性时，卡尔曼滤波算法的鲁棒性将受到一定程度的影响，而本文将噪声矩阵也进行实时更新操作，有效保证了噪声矩阵的统计特性，提升了实验鲁棒性。

1 锂离子电池参数辨识模型

1.1 锂电池二阶RC 等效电路模型

蓄电池模型参数辨识结果的精确度对其SOC 估计具有很大的影响，目前国内外常用的等效电路模型主要有Rint 模型、PNGV 模型、Thevenin 模型、多阶RC 环路模型等。其中多阶RC 环路模型以其精度较高、动态适应性好等优点被广泛应用于蓄电池的SOC 估计中[2]，在采用多阶RC 环路模型时，随着RC 网络数的增多其参数辨识精度也会随之提高，然而却会导致计算量过大等问题，在综合考虑精度以及计算量的前提下，本文选取二阶RC 等效电路模型进行建模。

图1中，R0为电池欧姆内阻，Rs、Cs分别表示电池电化学的极化电阻和极化电容，Rl、Cl分别表示电池浓度的极化电阻和极化电容。将图1所示电路用基尔霍夫定律表示如下：

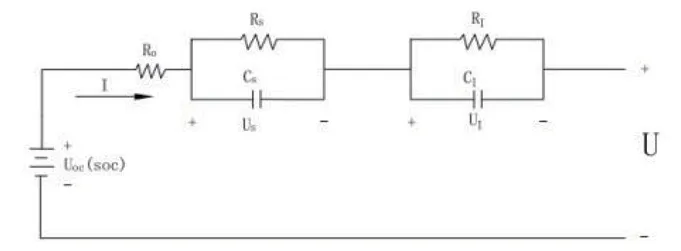
图1 蓄电池等效电路模型

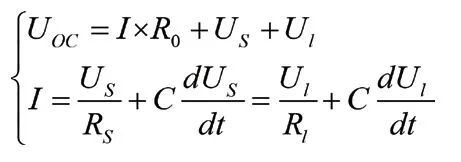
1.2 离散系统模型

参数辨识过程中的一系列数学表达式应为离散形式，而上述基尔霍夫定律所得的系统方程为连续时间模型，因此需对其进行拉普拉斯变换，同时使用脉冲响应不变法对其进行离散化等处理，最终得到系统的状态空间模型如下，式中T 为采样周期（本文取1s），QN为电池容量：

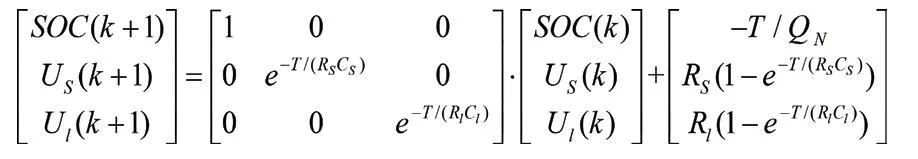
1.3 参数辨识

由于锂电池充放电是动态过程，且在充放电过程中锂电池的等效电路参数一直随着充放电深度的变化而变化，因而离线最小二乘辨识算法在实际应用中误差就会很大，也就不适合工程应用，而传统的递推最小二乘算法根据每次新的实验数据，在前一次估计值的基础上利用新数据对前估计值修正，从而递推得出新的估计值。只是在参数辨识中，递推辨识最小二乘法在递推迭代的过程中旧数据不断积累，特别是在锂电池系统中，实验过程中会存在大量数据，以至于新数据会被旧数据所淹没。因此本文提出一种带遗忘因子的递推最小二乘算法，引入遗忘因子对旧数据进行处理，有效克服了“数据饱和”现象，起到突出新数据的特点。

具体辨识过程为：以I(k)为输入、SOC(t)为输出，在已知参数R0、Rs、Rl、Cs、Cl初值的情况下，将初值代入状态空间模型进行蓄电池SOC 估计，通过测量蓄电池端电压U 和输入电流I，结合估计所得的SOC 以及状态空间模型，运用含遗忘因子的最小二乘算法进行参数辨识，最后利用辨识所得结果重新进行SOC 估计，以此类推。

1.4 输出方程及BP 神经网络拟合

模型参数辨识前需要进行OCV-SOC 拟合，在得到OCV-SOC 拟合曲线时常采用多项式拟合，然而多项式函数拟合非线性关系却存在过拟合的问题，而BP 神经网络模型却能很好地模拟出电池的外部特性，且在数据量较多的情况下，其精度也有一定的保证，因此本文通过恒流间歇放电获取实验数据，在此基础上采用BP 神经网络拟合OCV-SOC 曲线。本次实验选用9阶多项式进行图像拟合，但因过拟合现象的存在，使得拟合结果不具有普适性，而BP 神经网络通过大数据训练可以很好地避免过拟合现象，其拟合优度见下：

采用多项式拟合的9阶输出端电压表达式为：UOC(SOC)=0.03472×SOC9-0.008522×SOC8-0.1535×SOC7+0.03415×SOC6+0.2255×SOC5-0.05506×SOC4-0.1098×SOC3+0.01943×SOC2+0.04437×SOC1+3.3

当阶数达到9阶时，改变相应数值时会发现拟合效果急剧下降，也就说明此时已出现了过拟合现象，而降低阶数又会较大程度上影响拟合精度，因此最终决定采取BP 神经网络进行曲线拟合。利用BP 神经网络拟合开路电压的函数表达式为[3]：U(k)=NN[SOC(k)]-US(k)-Ul(k)-R0×I(k)，神经网络拟合残差图如图2，两种算法的OCV-SOC 拟合曲线如图3。

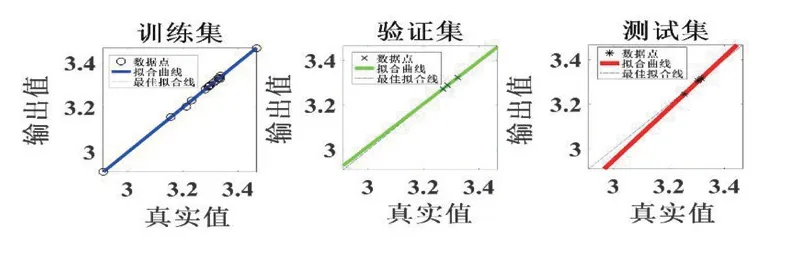
图2 BP 网络拟合残差图

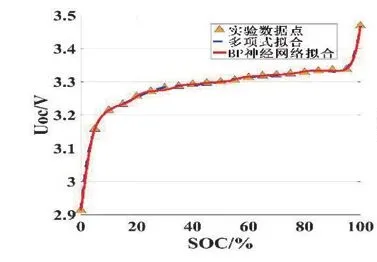
图3 多项式拟合和BP 神经网络拟合对比图

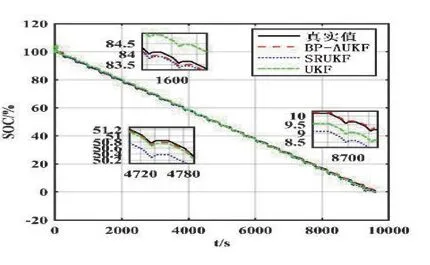
图4 不同滤波算法估算精度对比图

2 AUKF 算法估计锂电池SOC

由于传统的UKF 算法仅是对原高斯分布数据按一定规则采样，采取非线性变换后对均值等进行加权处理，并没有改善其高维状态下计算量大的缺点，因此本文提出噪声矩阵可以实时变换的AUKF 算法，有效提升了SOC 估计的实时性和准确性。

初始化式(1)；选取采样（sigma）点式(2)、同时确定加权系数式(3)，式中求解采样点均值的权值记为ωm，求解采样点协方差的权值为ωc，α 为修正参数，β 取2；时间更新式(4)；测量更新式(5)，式中g[Xik+1|k]是观测真实值，Zik+1|k为观测预测值，L(k)为增益矩阵，Zk+1是实际测量值；噪声矩阵更新式(6)，式中y(k+1)为观测值，Qk+1为过程噪声协方差，Rk+1为观测噪声协方差。对于上述步骤从选取采样（sigma）点进行循环迭代，当收敛到一定精度时即可认为获取了SOC 最优状态估计。与传统卡尔曼滤波算法相比，AUKF 算法既保留了无迹变换时避免了计算雅可比矩阵的优点，又通过对噪声矩阵的实时更新保证了估算的实时性与准确性。

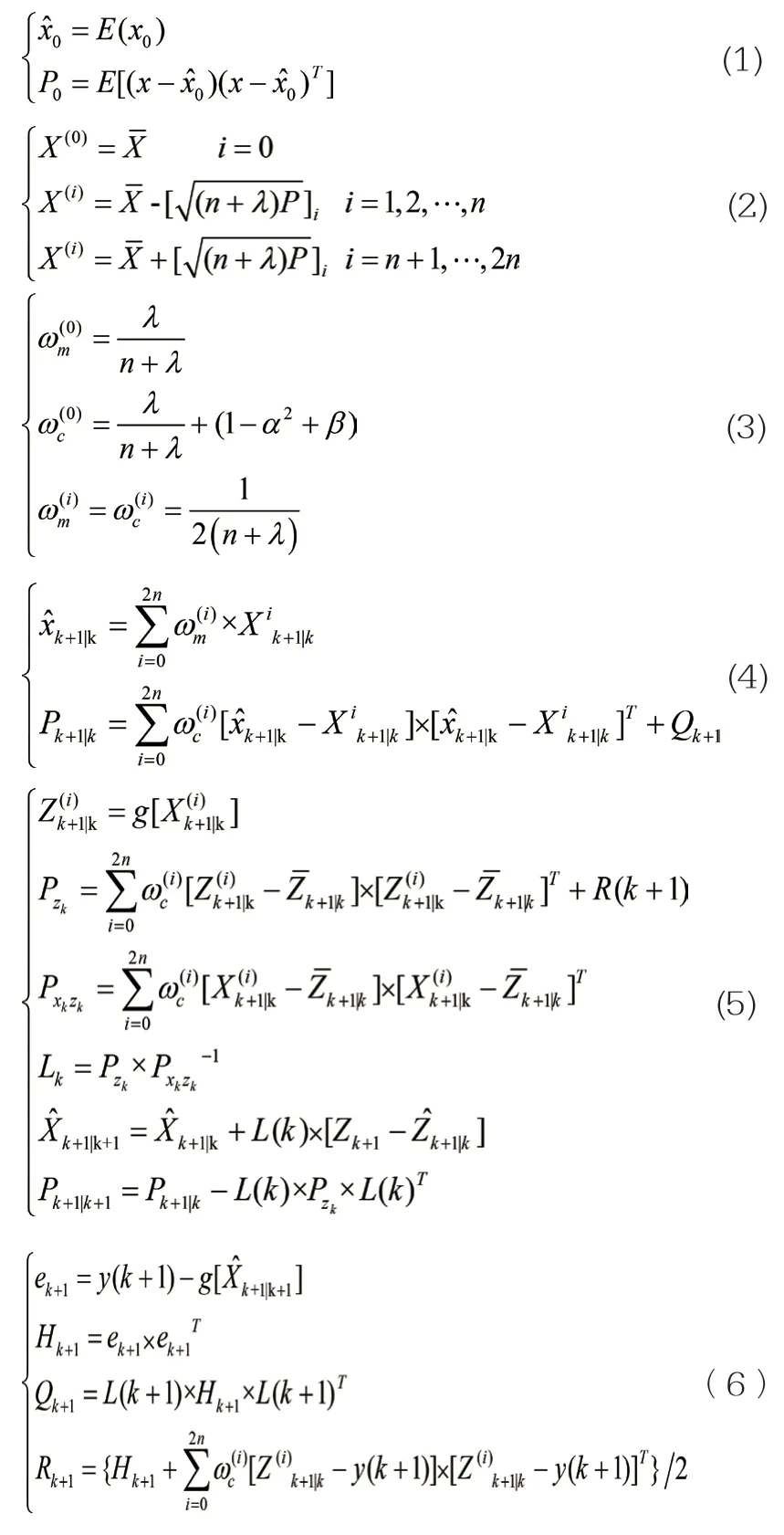
3 实验验证

SOC 初值为100%时从图像中的前面一部分可知，算法启动后误差逐渐收敛，当误差收敛至一定范围时基本稳定，收敛至一定范围时BP-AUKF 算法所需迭代的次数最少，也就是说BP-AUKF 算法的收敛速度较UKF、SRUKF 算法收敛速度更加快；同时，算法稳定后BP-AUKF 算法的误差小于UKF、SRUKF 算法的误差，也就是说BP-AUKF 算法的参数辨识精度更高，可见BP-AUKF 算法的优越性。

当验证实验结果的鲁棒性时决定将预测初值改为80%，由拟合结果可看出，即使将初值改为80%预测值也能以较快速度收敛，虽比传统UKF 算法收敛略慢一些，但总体效果依然较为令人满意，且拟合精度更高，最大估计误差保持在0.5%左右，因此本实验具有一定的鲁棒性。

图5 不同滤波算法估算误差对比图

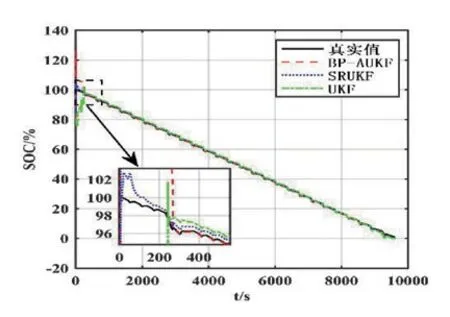
图6 初值为80%时SOC 估计

综上，由于锂离子电池在正常工作时电池内部也会发生较为复杂的电化学反应，因此提出二阶RC 等效电路模型，力求在准确模拟电池外特性的前提下也不忽略电池的内部反应，据此提高研究的实用性。在结合含遗忘因子的递推最小二乘算法（FFRLS）、BP 神经网络拟合以及自适应无迹卡尔曼滤波（AUKF）的前提下，有效将SOC 估计最大误差稳定在0.5%左右，并得到如下结论：

遗忘因子取值范围为0.95～1，本文取0.996，既证明了历史数据确实对实验结果具有一定影响，也说明了在结合多种精度较高的方法的前提下，数据饱和的现象已有所改善，使得遗忘因子更接近1；本文实验基于9602组实验数据，在如此庞大的数据组下，可见BP 神经网络拟合优度相对于多项式拟合确实有了较为显著的提升，从而使得后期SOC 估计精度有所提高；由几种滤波方法的对比可见，BPAUKF 算法有效将SOC 估计精度误差控制在0.5%左右，更有利于电池管理系统的稳定。