施密特正交化的几何解释及代码实现
陈 健,龚 萍
(攀枝花学院,四川 攀枝花 617000)
线性代数中,若要探究高维度线性空间的相关问题,标准正交基必不可少,当成功建立起标准正交基后,当前空间的所有向量都可以利用此标准正交基表达。例如:在解决三维空间中立体几何问题时,可优先建立空间直角坐标系,这能够帮助学者简化诸多复杂问题,在构造所需标准正交基时,则需要使用施密特正交化方法[1],利用向量之间基本关系,以三维空间为例,依据向量间的基本关系和内积定理,演示施密特正交化过程,探讨和解释施密特正交化的几何意义,并用代码实现施密特正交化方法计算,帮助学者理解施密特正交化空间几何意义。
1 施密特正交化几何意义
施密特正交化的目的是利用向量的基本运算和向量内积的定理对一个线性无关向量组构造出一个等价的正交向量组。将以三维空间为例,依据向量的基本知识演示施密特正交化的步骤,向学者解释施密特正交化的几何意义。
1.1 基本向量、内积、线性相关知识的解释
首先解释向量的基本运算,内积的定理和向量的线性相关性:

图1Fig.1

图2Fig.2
由向量内积的定理:设n维向量a与b,满足[a,b]=0,则向量a与b正交[3]。
若给定向量组A:a1,a2,…,am,若存在不全为0的数k1,k2,…,km,使得k1a1+k2a2+…+kmam=0成立,则向量组A是线性相关的;从几何上理解,如:若一组向量线性相关,则它在二维空间中时,任意两个向量是共线的,而三维空间中,则其中任意三个向量是共面的[4];若k1a1+k2a2+…+kmam=0当且仅当k1,k2,…,km全都为0时成立,称向量组a1,a2,…,am线性无关,意味着向量组在二维空间中任两个向量不共线,在三维空间中任三个向量不共面。
1.2 从几何角度解释施密特正交化
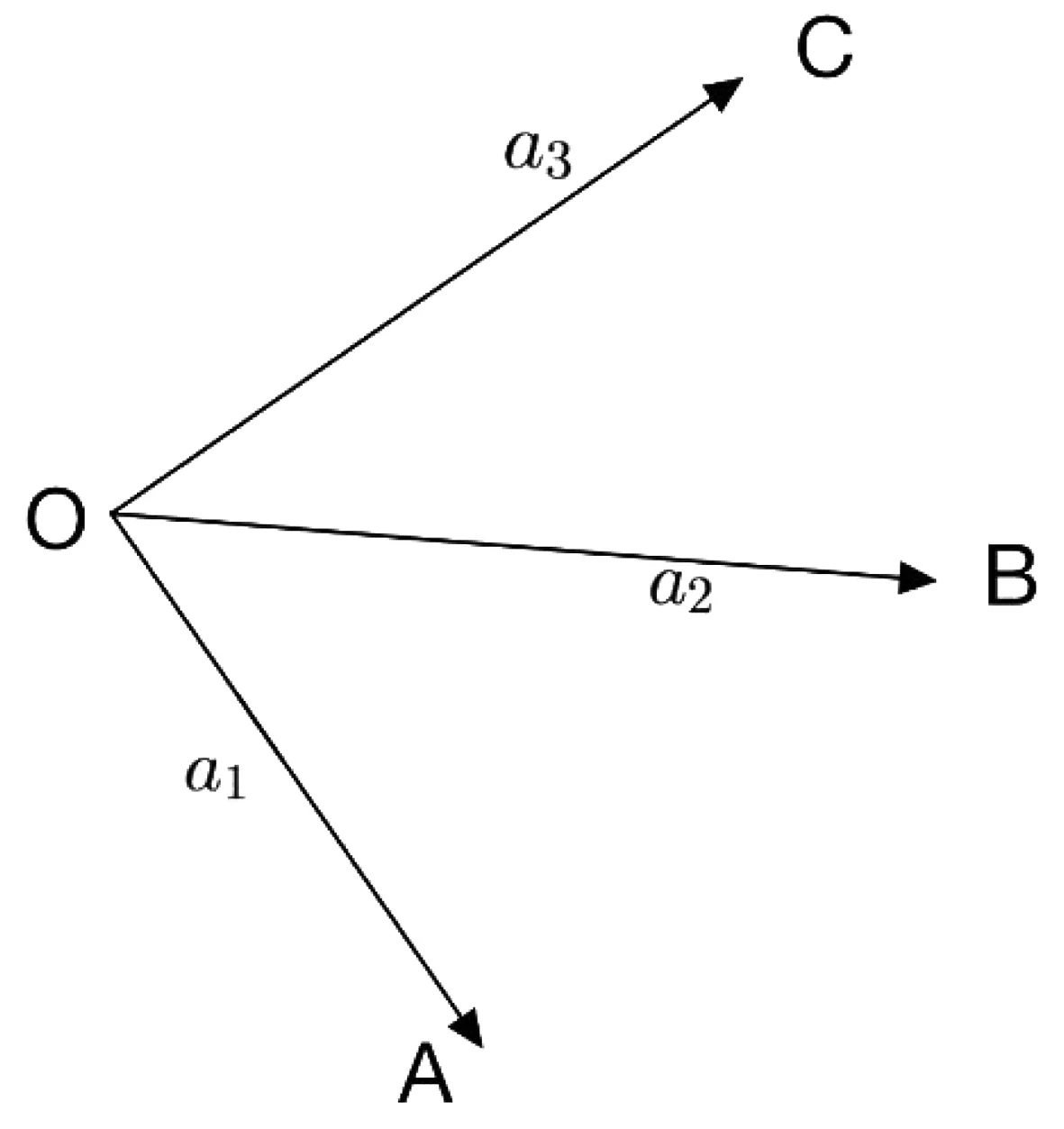
图3Fig.3


图4Fig.4
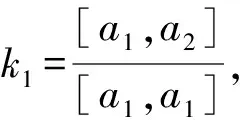

图5Fig.5



同理则可以得到施密特正交化的公式:
当前有一组线性无关的n维向量组a1,a2,a3,…ar,则有[6]:
b1=a1
…
2 利用计算机代码实现
2.1 代码内容
根据施密特正交化求等价正交向量组的基本公式和思路,设计了以下代码来实现计算向量以达到正交化效果[7]。
核心代码为:
int k=0;
double x=0;//施密特正交化公式中分式的分子
double y2=0;// 施密特正交化公式中分式的分母
double u[100];//正交化后的系数
//取输入的第一个向量置为正将向量组的第一个向量
for(int i=1;i { //从输入的第二个向量开始正交化 for( k=0;k { for(int j=0;j { x +=vector[i][j]*vector[i-1-k][j]; y2 +=vector[i-1-k][j]*vector[i-1-k][j]; u[k]=x/y2; } for(int j=0;j { vector[i][j]=vector[i][j]-x/y2*vector[i-1-k][j]; } x=0; y2=0; } } //将得出的正交化向量单位化 for(int i=0;i { for(int j=0;j { x += vector[i][j]*vector[i][j]; } u[i]=sqrt(x); x=0; } 假设数据为:a1=(1,0,1)T,a2=(1,1,0)T,a3=(0,1,1)T,利用施密特正交化方法,理论得出的值是: 结果: 代码能够计算出施密特正交化后正交向量组,但由于计算机的精度与人工计算的精度不同,计算机中存储数据的方式及计算数据的逻辑先后都契合机器的存储和计算[8],而人工计算会使用约分等技巧计算,导致某些情况计算机运算的正交化向量与人工计算所得的值不符合,从而产生一定误差。但因计算机运算的精度会更高,则计算机程序得出的正交向量组更趋近于正确的正交向量组。2.2 运行效果

2.3 结果分析

