基于Bayes判别法的结冰现象资料序列订正*

温华洋 朱华亮 马文周 邱康俊 张苗苗 刘 壮

1 安徽省气象信息中心，合肥 230031 2 合肥工业大学，合肥 230009

提 要： 针对安徽省81个国家级地面气象站1961—2018年结冰现象资料序列，采用要素一致性、内部一致性、空间一致性等方法进行数据质量控制，基于质量控制后的正常年份数据进行Bayes判别模型训练，应用训练所得模型完成异常年份结冰数据的订正。结果表明：安徽省共有38个台站累计84年的年结冰日数质量控制检查异常，年结冰日数异常年份主要集中在1961—1970、1988—1999和2015—2017年，造成年结冰日数异常的原因有部分台站历史观测任务简化、气象台站分类调整以及地面气象观测业务改革等。利用Bayes判别法构建了多个结冰现象判别模型，经检验发现，模型1和模型3具有较高的判识正确率、命中率、TS评分以及较低的误警率。考虑计算的简便性，选用模型1对异常年份结冰数据进行逐日订正。通过六安站、太和站和无为站异常年份结冰现象订正结果对比发现，基于Bayes判别法的结冰现象判别模型，对不同时间段内、不同原因造成的结冰现象观测记录异常的订正均较为合理，订正后的年结冰日数变化趋势更符合实际情况，表明采用Bayes判别模型订正结冰现象是合理、可行的。

引 言

结冰(又称冻结)指露天水面冻结成冰，包括器皿中的水冻结成冰，是日常生活中比较常见的自然现象，但其通常与低温冷害相伴随，对人类的生产生活、动植物的生长有较大的影响(中国气象局，2003；唐熠等，2019；刘洪兰等，2014；马树庆等，2015;李刚等，2020)。如在冬季的雨雪天气，高速公路、机场跑道上会出现积雪或结冰现象，由此引发的交通事故、交通延误等，已成为社会各界广泛关注的热点问题(Wang et al，2008；丁国香等，2018；蒲晓虎等，2014)。因此，气象部门对结冰现象的监测和预报非常重视，高质量、长序列的结冰资料有利于气候变化分析、农业气象和道路交通的预报与服务，也是开展有效灾害预防、应急救援等活动的科学依据(张志富等，2015；张庆奎等，2020；舒斯等，2019；白永清等，2016；Toms et al，2017)。

从20世纪50年代起，我国部分气象站就开始记录结冰现象，至今已形成了约60年的结冰现象观测资料，这些观测资料在农业、交通等领域的气象服务中发挥着重要作用，但同样存在着部分台站因历史观测任务简化、观测方式多次调整等诸多原因造成的数据质量不高的问题。余予等(2018)研究发现1954—1979年全国共有662个台站累计6 328年实际未观测和记录结冰现象，1981年前有839个台站累计1 453年存在明显漏记结冰现象情况。如果直接使用这些原始观测资料而不进行有效地质量控制，对于结冰现象长期变化趋势分析等会得到不同的甚至相反的结论。因此，在使用结冰现象观测资料前需进行严格的质量控制和合理的数据订正。目前，国内外主要基于界限值、内部一致性和人工审核等方式对结冰现象观测数据进行检查(范邵华等，2018；任芝花等，2007；2015；廖捷和周自江，2018；江益等，2018；刘小宁和任芝花，2005；陶士伟等，2009；闵锦忠等，2018)，质量控制方法较为简单，如在历史资料的数字化过程中，仅对数据的完整性、规范性进行了检查，对出现的空白记录或者缺测记录无法进一步确认处理(范邵华等，2018)；任芝花等(2015)设计的“台站-省级-国家级”三级质量控制只能对明显错误的数据进行缺测处理，无法确认某日是否出现结冰现象。在结冰现象观测数据订正方面，国内外相关研究较少，采用的线性回归法(余予等，2018)也仅能完成对年(或月)结冰日数的插补，较难认定某天是否发生结冰现象。为此，本文结合气温、地表温度等气象要素观测值对安徽省81个国家级地面气象站结冰现象观测资料进行了严格的质量控制，采用Bayes判别法构建了日结冰现象判别模型，并探讨了判别模型对结冰现象资料序列的逐日订正效果，旨在通过质量控制和数据订正形成高质量、长序列的结冰现象资料序列，为结冰现象的气候变化分析等提供科学依据。

1 资料与方法

1.1 资料与处理

本研究使用的资料包括安徽省81个国家级地面气象站1961—2018年的日结冰现象观测资料(当日是否出现)、日最低气温(单位：℃)、日最低地表温度(单位：℃)，源自对应站点的地面气象月报表A文件。根据日最低气温和日最低地表温度观测值，对日结冰现象是否出现的资料序列进行初步质量控制。若某日出现结冰现象，且日最低气温和日最低地表温度均大于10℃，则判定该日的结冰现象记录错误，将该日订正为无结冰现象；如果日最低气温(或日最低地表温度)缺测，则在该日定时气温(或地表温度)中取最小值进行替代。依据《地面气象观测规范》(中国气象局，2003)统计得到安徽省81个国家级地面气象站1961—2018年的年结冰日数序列。

1.2 研究方法

为了更好地完成结冰现象资料序列的订正，采用要素一致性、内部一致性、空间一致性等方法对年结冰日数序列进行质量控制，方法和步骤如下：

第一步进行要素一致性检查。针对各站计算年结冰日数序列与年最低气温<0℃日数序列间的相关系数(R)。选取相关系数R>0.9且通过0.05的显著性水平检验的台站，利用这些台站的年结冰日数(y)和年最低气温<0℃日数(x)，求取两者间线性拟合公式。利用线性拟合公式估算各站每年的结冰日数，若某年观测值比估算值偏低50%，则认为该年结冰现象数据异常，对其进行标记。

第二步进行内部一致性检查。基于完成要素一致性检查后的正确结冰现象数据，计算各站年结冰日数的均值(μ)和标准差(σ)，若某年结冰日数位于区间[μ-3σ，μ+3σ]之外，则认为该年结冰数据异常，对其进行标记。

第三步进行空间一致性检查。基于内部一致性检查后的正确结冰现象数据，为待检验站点(以下简称待检站)构建参考序列，参考站选取的步骤与标准为：(1)与待检站的海拔高度差不超过200 m，地理环境相似；(2)与待检站的年平均气温序列相关系数R>0.6且通过0.05的显著性水平检验；(3)与待检站的直线距离<100 km，且距离最近的5个气象站。若选取的参考站数量不足5个，则以实际数量计算，若参考站数量为0个，则不进行空间一致性检查。计算待检站年结冰日数相对参考站平均年结冰日数的偏差，若某年的相对偏差超过50%，则认为该年结冰数据异常，对其进行标记。

对经质量控制后的正常年份数据进行Bayes判别模型训练，应用所得的模型对异常年份结冰现象数据进行订正，其中Bayes判别模型训练方法和步骤(王斌会，2011；华连生等，2015)如下：

(1)计算训练样本集中日结冰现象不发生和发生的概率分别为P0和P1。

(2)假设某日的相关气象要素观测值X=(x1，x2,…,xn)′，其中x1,x2,…,xn表示日最低气温、日最低地表温度等。根据训练样本集计算该日结冰现象不发生和发生情况下观测到相应气象要素值X的概率P(X/Yi),i=0,1，其中Y0代表日结冰现象不发生，Y1代表日结冰现象发生。

(3)根据Bayes定理，计算在相应气象要素观测值X条件下该日结冰现象不发生或发生的概率P(Yi/X)：

i=0,1

(1)

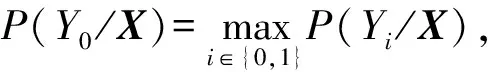
(2)

式中:μi=(μi1,μi2,…,μin)′，i=0,1;其中μi1,μi2,…,μin表示第i个总体中各变量的均值。协方差矩阵Σ=(σjl)n×n，协方差逆矩阵Σ-1=(σjl)n×n，其中σjl和σjl分别表示协方差矩阵及其逆矩阵中的第j行第l列元素，j=1,2,…,n,l=1,2,…,n。因为

式中“⟺”表示等价的意思，则有：

(3)

略去式(3)中与i无关的项，则可写为如下线性判别函数：

(4)

式中:

i=0,1,j=1,2,…,n

若Y0>Y1，认为该日无结冰现象；反之，认为该日有结冰现象。根据每日相关气象要素的观测值(日最低气温、日最低地表温度等)，利用式(4)可以完成逐日结冰现象的订正。

1.3 Bayes判识模型评价指标

为检验基于Bayes判别法建立的结冰判别模型判识效果，采用准确率(PC)、命中率(POD)、误警率(FAR)和TS评分(TS)等指标进行评估，具体计算公式如下：

(5)

(6)

(7)

(8)

式中：TN表示人工观测和模型判识都无结冰现象的日数，TP表示人工观测和模型判识都有结冰现象的日数，FN表示人工观测有结冰现象但模型判识无结冰现象的日数，FP表示人工观测无结冰现象但模型判识有结冰现象的日数。

2 数据质量控制检查结果分析

计算各台站年结冰日数与年最低气温<0℃日数间的相关系数，其中共有39个台站的相关系数R>0.9，且通过0.05的显著性水平检验。选用这39个台站的数据计算年结冰日数(y)和年最低气温<0℃日数(x)间的线性拟合公式为：

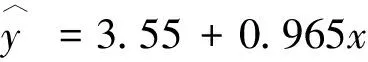
(9)

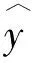
图1给出了1961—2018年结冰日数质量控制异常台站数逐年分布，从图中可以看出，年结冰日数异常年份主要集中在1961—1970、1988—1999和2015—2017年。这主要是由于20世纪60年代早期对结冰现象的观测要求较为简单(中国气象局，1961)，导致这类台站的结冰现象记录异常偏少，甚至为零。随着《地面气象观测规范》的修改和逐步完善(宁惠芳等，2014)，1970年之后这一问题得到了明显地扭转。1988年中国气象局制定实施的《地基气象探测系统发展方案》，将部分国家级地面气象观测站(如太和站、怀远站和怀宁站)划分为观测辅助站(吴增祥，2006)，对气压、天气现象等气象要素不做观测要求，造成记录的结冰现象显著偏少或无记录，1999年后观测辅助站重新归类为国家一般气象站(以下简称一般站)，所以1988—1999年有3～4个台站的年结冰日数出现异常。2014年中国气象局实施《地面气象观测业务改革方案》(中国气象局综合观测司，2013)，将国家基准气候站(以下简称基准站)和国家基本气象站(以下简称基本站)夜间天气现象连续观测(20时至次日08时)调整为4次整点(20、23、02、05时)观测，同时取消一般站夜间值守任务，这就造成夜间出现短时间结冰现象而漏记的情况，2018年安徽省加强了对月报表A文件中结冰现象的人工质量控制工作，因此，2015—2017年出现较多台站年结冰日数异常偏少现象，而2018年未见数据异常现象。图2给出了安徽省年结冰日数检查异常的台站分布，从图中可以看出，在全省年结冰日数异常的38个台站中，基准站和基本站共有10个站累计13年的年结冰日数异常，一般站共有28个台站累计69年的年结冰日数异常，异常站点及累计异常年数中一般站的占比都比较大，这与一般站观测方式的多次调整有关。在空间分布上，年结冰日数记录异常并无明显特征。

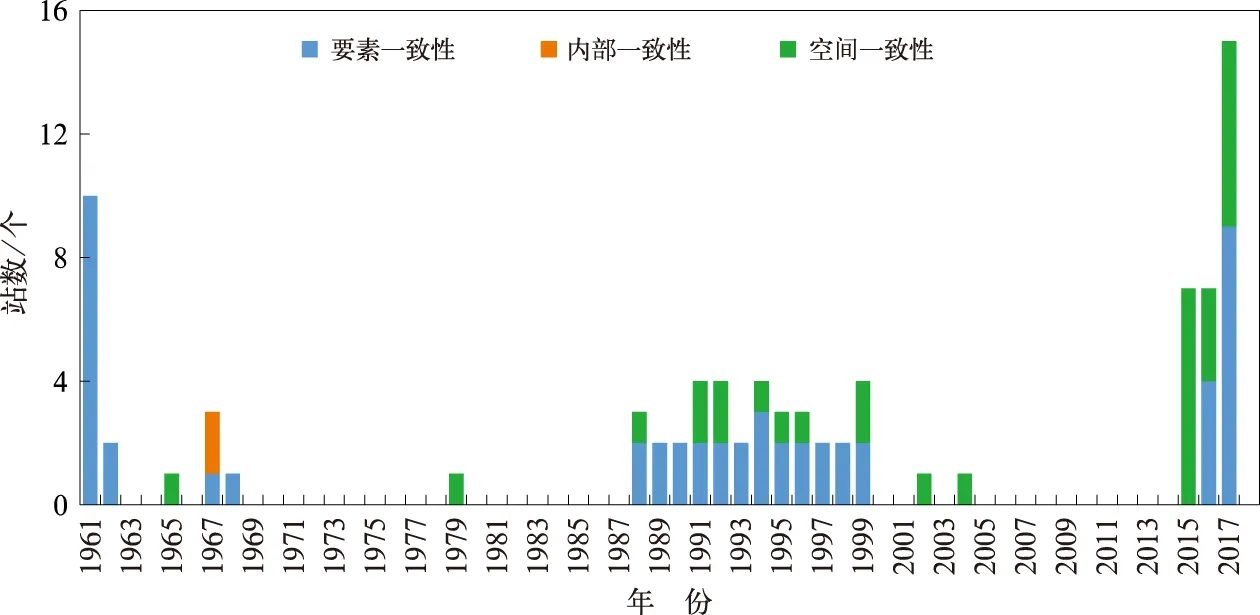
图1 1961—2018年安徽省年结冰日数异常台站数逐年分布Fig.1 Distribution of stations with abnormal annual icing days in Anhui Province from 1961 to 2018

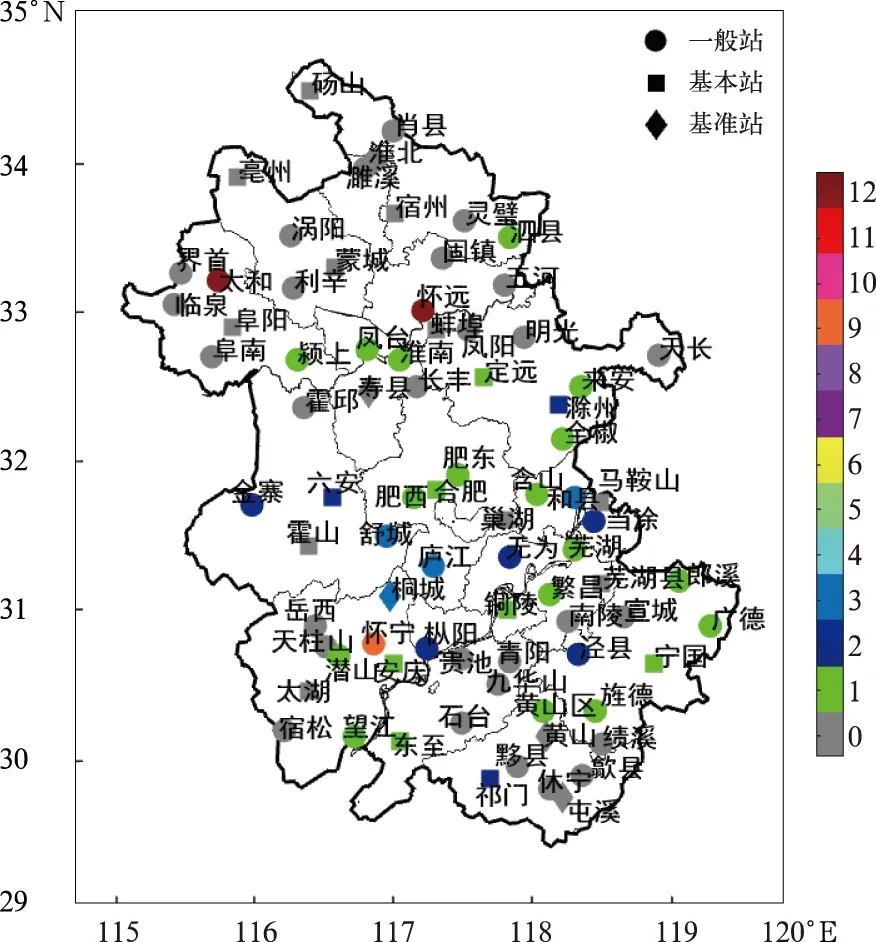
图2 1961—2018年安徽省各台站累计异常年数分布(单位：a)Fig.2 Distribution of cumulative abnormal years of stations in Anhui Province from 1961 to 2018 (unit: a)

3 结冰现象资料序列订正

3.1 Bayes判别模型建立

针对经过质量控制后的正确年份结冰现象数据，剔除日最低气温和日最低地表温度均大于10℃的日数据，得到较易发生结冰现象的日数据，共有数据1 203 734 d，随机选取80%作为模型训练数据集，剩余20%作为模型验证数据集。训练数据集中无结冰日数占比P0=0.66，有结冰日数占比P1=0.34。鉴于温度对结冰现象的影响，将日最低气温(Tmin)、日最低地表温度(Dmin)依次代入式(4)中建模，得到结冰现象判别模型1、模型2和模型3如下：

模型1(日最低气温判别模型)：

(10)

模型2(日最低地表温度判别模型)：

(11)

模型3(日最低气温和日最低地表温度判别模型)：

(12)

为考察模型1～模型3对结冰现象的判别能力，利用验证数据集对各模型进行检验，其中验证数据集中无结冰日为168 179 d，有结冰日为72 432 d，共计240 611 d。表1给出了各模型的正确率、命中率、误警率、TS评分等检验评价指标，模型1和模型3具有较高的判识正确率、命中率和TS评分，且模型的误警率较低，模型2的判识效果不如模型1和模型3，表明可用模型1和模型3对日结冰现象进行判识，但两者判识效果差异不大，且模型1比模型3少一元变量，更便于计算，因此，选用模型1对质量控制检查异常年份结冰数据进行逐日订正。

表1 基于验证数据集的各模型判别效果Table 1 Discrimination effect of each model based on validation data set

3.2 基于Bayes判别模型的结冰序列订正

针对数据质量控制标记的结冰现象记录异常年份数据，利用模型1进行逐日判别。如果模型判别结果与人工记录结果不一致，则将该日结冰现象订正为模型判别结果；否则不进行订正。如果某日最低气温缺测，则在该日定时气温中取最小值进行替代。

通过上述方法对安徽省38个台站累计84年的异常年份数据进行订正，共订正了2 949 d的结冰现象记录，订正数据量占异常年份总数据量的9.5%，占比较少。基于订正后的结冰现象资料序列重新进行要素一致性、内部一致性、空间一致性等检查，发现仍有2个台站累计2年的年结冰日数异常(表2)。从表2中可以看出，望江站模型判别结冰日数相对参考站平均结冰日数明显偏少，导致该站2017年订正后的年结冰日数未通过空间一致性检验。经统计发现，人工记录结冰日数明显少于年最低气温<0℃日数和年最低地表温度<-1℃日数，而模型判别结冰日数更接近于年最低气温<0℃日数和年最低地表温度<-1℃日数，表明望江站2017年人工观测结冰现象的记录中存在漏记的可能。淮南站1999年人工记录结冰日数和模型判别结冰日数相对于参考站平均结冰日数都明显偏少，所以该年结冰日数也未通过空间一致性检验，但人工观测结冰日数、模型判别结冰日数和年最低气温<0℃日数三者间都比较接近，故认为当年结冰现象人工记录正常。总体而言，经Bayes判别模型订正后，38个台站累计84年的异常年份数据中有36个台站累计82年通过质量控制检查，虽有2个台站累计2年的年结冰日数未通过检验，但模型判别结果比较符合台站自身的实际情况，表明经Bayes判别模型订正后结冰现象数据质量得到明显提升。

表2 异常站点年结冰日数的质量控制结果Table 2 The quality control results of revised annual icing days at abnormal stations

3.3 订正结果对比

以六安站、太和站和无为站为例，考察Bayes判别模型对质量控制检查异常年份结冰现象的订正效果，并与参考序列进行对比，其中参考序列的构建选用通过质量控制的站点数据，具体参见空间一致性检验参考站选取的方法与步骤。六安站的年结冰日数异常年份出现在1967年和1968年，这两年人工观测的年结冰日数分别为23 d和8 d，利用模型1订正后的年结冰日数分别为69 d和56 d，模型订正值与人工观测值差异较大，但与参考序列的年结冰日数更为接近(图3a)。在年结冰日数变化趋势上，订正序列的趋势与参考序列的趋势更为接近，且均为下降趋势，表明Bayes判别模型对六安站1967年和1968年的结冰现象订正效果较好。太和站在1988—1999年为观测辅助站，对结冰现象不做观测要求，造成1988—1999年的结冰现象未做记录，通过模型1订正后，1988—1999年订正序列平均年结冰日数为63.8 d，最低年结冰日数为42 d，最高年结冰日数为82 d，与参考序列的平均绝对差值为6.5 d，最大绝对差值为12.2 d，而1961—1987年年结冰日数原始序列与参考序列的平均绝对差值为5.6 d，最大绝对差值为15.4 d，2000—2018年年结冰日数原始序列与参考序列的平均绝对差值为7.1 d，最大绝对差值为12.4 d，表明1988—1999年年结冰日数订正序列与参考序列的误差在合理范围内。从变化趋势上看，订正序列的变化趋势与参考序列更接近(图3b)，且订正序列线性趋势线的拟合优度R2要明显大于原始序列趋势线的R2，表明利用订正序列得到的趋势线更可靠。总体看来，Bayes判别模型对太和站1988—1999年的结冰现象订正较为合理。图3c给出了无为站订正前后1961—2018年年结冰日数序列，无为站2016年和2017年人工观测的结冰日数分别为12 d和8 d，相较于往年观测值和参考序列都明显偏少，订正后的结冰日数分别为26 d和21 d，与参考序列更为接近，也更符合序列变化趋势。

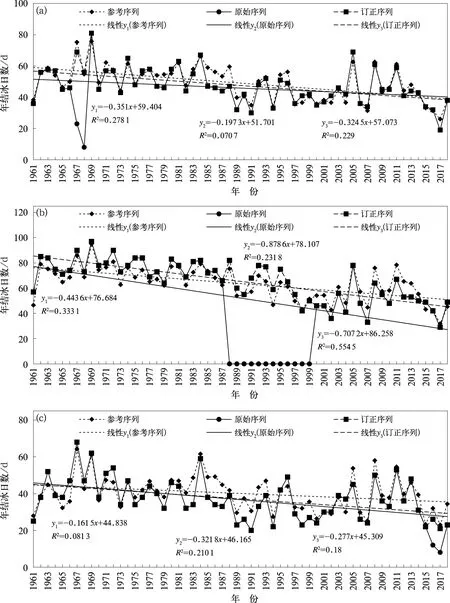
图3 1961—2018年六安站(a)、太和站(b)和无为站(c)年结冰日数序列Fig.3 Annual icing days series of Lu’an Station (a), Taihe Station (b) and Wuwei Station (c) from 1961 to 2018

通过六安站、太和站和无为站异常年份结冰现象订正结果对比发现，基于Bayes判别法的结冰现象判别模型，对不同时间段、不同原因造成的典型的结冰观测记录异常的订正均较为合理，订正后的年结冰日数变化趋势更符合实际情况，表明采用Bayes判别模型订正结冰现象是合理、可行的。

4 结论与讨论

(1)本研究采用要素一致性、内部一致性、空间一致性等方法对安徽省81个台站1961—2018年年结冰日数序列进行更细致的质量控制，与余予等(2018)中质量控制方法相比，本研究所采用的方法更为严格，主要体现在：①本研究内部一致性检查时采用3倍标准差，而余予等(2018)采用5倍标准差；②本研究采用了空间一致性检查，而余予等(2018)未进行空间一致性检查。

(2)年结冰日数质量控制结果表明，安徽省共有38个台站累计84年的年结冰日数质量控制检查异常，年结冰日数异常年份主要集中在1961—1970、1988—1999和2015—2017年，造成年结冰日数异常的原因有部分台站历史观测任务简化、气象台站分类调整以及地面气象观测业务改革等。余予等(2018)对安徽省1981年之前的年结冰日数质量控制发现，共有1站累计1年未记录结冰现象，有8站存在1～2年的年结冰日数显著偏低。从图1可以看出，本研究发现的1981年之前的年结冰日数异常站数和累计年数要明显多于余予等(2018)的质量控制结果，这也佐证了本研究质量控制标准比余予等(2018)的质量控制标准更为严格。

(3)针对质量控制后的正确年份结冰现象数据集，采用Bayes判别法建立模型1、模型2和模型3。经检验发现，模型1和模型3各项评价指标均较好。考虑计算的简便性，选用模型1对质量控制检查异常年份结冰数据进行逐日订正。通过订正结果对比发现，基于Bayes判别法的结冰现象判别模型，对不同时间段内，不同原因造成的结冰现象观测记录异常的订正均较为合理，订正后的年结冰日数变化趋势更符合实际情况，表明采用Bayes判别模型订正结冰现象是合理、可行的。

(4)本研究发现部分台站历史观测任务简化、气象台站分类调整、地面气象观测业务改革等引发了安徽省部分台站的年结冰日数异常问题，这些问题势必在全国其他地区同样存在，余予等(2018)仅对1981年前的年结冰日数进行质量控制，就发现全国1954—1979年共有662个台站累计6 328年实际未观测和记录结冰现象，1981年前有839个台站累计1 453年存在明显漏记结冰现象情况。因此，在使用全国结冰资料进行气候变化分析时，还需进行有效的质量控制和序列订正。本研究所用方法对全国范围内的结冰资料的质量控制和订正提供了一种参考，但其质量控制和订正效果还有待于进一步探讨。