非粘结钢管脐带缆弯曲滞回参数敏感性分析❋

于晶晶， 郭海燕， 刘 震， 崔 鹏

(中国海洋大学工程学院， 山东 青岛 266100)

海洋脐带缆是深远海油气开采中的核心装备之一，由于安装和在位运行期间所受环境荷载的复杂性，其截面基本力学模型为典型多层多构件非粘结螺旋缠绕结构[1]。

非粘结钢管脐带缆的弯曲刚度是衡量其弯曲性能的一项重要指标。在脐带缆的整体分析中，弯曲刚度是进行动态荷载分析的前提。因此近年来国内外学者针对非粘结脐带缆的弯曲行为展开了大量探索和研究。随着研究的深入学者们发现非粘结脐带缆在受弯时内部管件会发生相对位移，出现与弹塑性材料进入塑性时类似的迟滞特性。Vaz等[2]提出复杂层状结构由于层间的滑动摩擦会表现出双线性滞回弯矩-曲率关系。卢青针[3]、肖能[4]等用ANSYS建立脐带缆全三维有限元模型来分析其非线性弯曲行为，并将数值模拟与理论和实验结果进行了对比验证。李英等[5]、冯雅萍[6]应用Darboux标架推导弯曲荷载作用下单根螺旋结构的滑移变形，建立受力平衡偏微分方程，并用ABAQUS数值模拟结果验证了理论公式的准确性。李晓月[7]考虑了填充对脐带缆截面弯曲性能的影响，计算得出了无铠装钢管脐带缆的弯曲刚度理论和模拟值。张宁等[8]针对脐带缆进行了全尺寸弯曲刚度测试并给出了一种弯曲刚度计算方法对测试结果进行了分析。这些研究均未对摩擦系数、外压大小、螺旋角度等敏感性参数的变化以及是否考虑填充单元等对脐带缆弯曲滞回特性进行系统研究。

本文利用ABAQUS软件建立非粘结钢管脐带缆弯曲滞回性能研究的有限元模型，针对非粘结钢管脐带缆的常见设计参数对弯曲滞回效应的影响进行敏感性分析，进一步探索其变化规律和弯曲不同阶段的刚度值，以期为脐带缆生产厂家对不同设计参数组合情况下脐带缆弯曲刚度不同阶段标准值的确定提供参考。

1 非粘结钢管脐带缆弯曲理论模型

由于管件间接触滑移等非线性行为的存在，非粘结钢管脐带缆弯曲刚度的理论分析较拉扭工况更为复杂。推导基于合理的简化与假设，一般将管缆的弯曲状态分为无滑动和全滑动两种。从Witz等[9]提出的弯曲模型中可得管缆的整体弯曲刚度如下：

无滑动状态：

(1)

全滑动状态：

(2)

式中：EI为脐带缆整体弯曲刚度；(EI)0为中心管件弯曲刚度；EiIi、EiAi分别为第i根螺旋管件弯曲刚度与拉压刚度；Ri为第i根螺旋管件节圆半径；αi为螺旋角度。

Costello[10]考虑到螺旋构件泊松比的影响，得到脐带缆整体弯曲刚度公式:

(3)

Roberto等11]考虑滑移后结构层间的径向接触，提出全滑动状态的整体弯曲刚度公式:

(4)

式中：EcIc为轴向管件的弯曲刚度；GiJi为螺旋构件的扭转刚度。

2 非粘结钢管脐带缆有限元模型的建立

2.1 脐带缆外形参数及材料属性

非粘结钢管脐带缆主要是由功能性单元(包括钢管单元、电缆单元、光纤单元)和护套单元以及填充单元组成。本文选取某工程实例中的无铠装非粘结钢管脐带缆作为建模分析的对象。其外形参数和材料属性如表1和2所示。

表1 非粘结钢管脐带缆尺寸

表2 材料属性

其中，螺旋管件层包含5根钢管单元、3根电缆单元和1根光纤单元，其外部均包裹聚合物保护层。9根管件的排布及细部尺寸如图1所示。

图1 非粘结钢管脐带缆截面示意图

2.2 接触设置及载荷选取

为了较好地模拟非粘结钢管脐带缆的接触和变形，本文采用C3D8R三维实体减缩积分单元。选择面面接触模拟功能管件层内部及其与中心和外部聚合物保护层之间的接触。接触面法向设置为不可穿透的硬接触，切向允许发生有限滑移。将端面耦合于中心节点处，便于边界条件的设置减小边界效应的影响。采用材料力学纯弯曲梁模型，一端固定一端施加转角位移荷载。经推导得纯弯曲梁的弯曲刚度为：

(5)

式中：EI为纯弯曲梁的弯曲刚度；M为固定端弯矩；L为纯弯曲梁长度；fB为自由端竖向位移。

图2 弯曲荷载加载曲线

2.3 分析求解与网格精度

ABAQUS求解非线性问题主要采用显式和隐式两种计算方法，在动态分析中分别对应着直接积分法中的中心差分法和Newmark法。比较两种算法，显式中心差分法更适合研究爆炸、高速运动冲击等问题，有较好的稳定性更易于收敛，但由于其实质是使用差分代替微分，并且对位移和加速度采用线性外插，这就限制了步长不能过大，否则该方法算得的结果无法保证准确。而Newmark法则常见于计算低频占主导的动力问题，每一个增量步内都需要迭代求解大型线性方程组，虽然计算过程需要占用相当数量的计算机资源且不容易收敛，但胜在其计算结果的正确性可以得到保证。因此进行弯曲滞回分析时采用隐式算法，由于接触复杂带来的收敛性问题采用多分析步的方法可以很好地解决。

由于滞回现象主要由接触面的滑移引起，所以接触面上网格划分精度至关重要，本文有限元模型网格划分采取图3的形式。

图3 非粘结钢管脐带缆有限元模型

2.4 数值模型值与理论值的对比验证

为了验证模型计算结果的准确性，取摩擦系数为0，进行建模分析，结果如图4。从图中可以看出， a曲线的加载阶段和卸载阶段几乎重合，弯曲迟滞现象不明显，该情况与公式(2)和公式(3)不考虑摩擦时的理论计算结果相吻合。

图4 摩擦系数为0时弯矩—曲率曲线

图4曲线经拟合得到脐带缆弯曲刚度为1 952.8 N·m，与根据弯曲理论公式(2)、(3)求得的弯曲刚度理论值2 023.9和2 031.0 N·m接近，误差为3.5%和3.8%。经分析误差产生的原因为结构建模进行网格划分后，管件间会存在一定的初始间隙，导致有限元模拟值略小于理论值。但误差在容许范围内，说明该有限元模型可以很好的模拟非粘结钢管脐带缆的受弯性能。

3 弯曲滞回性能影响分析

3.1 摩擦系数对弯曲滞回的影响

非粘结钢管脐带缆受弯产生的层间摩擦滑移是引起弯曲滞回的主要原因。这就使得摩擦系数对弯曲滞回的影响不可忽视。考虑螺旋角度为10°，设置摩擦系数为0.2、0.4、0.6和0.8进行分析，得到其弯矩-曲率变化关系如图5所示：

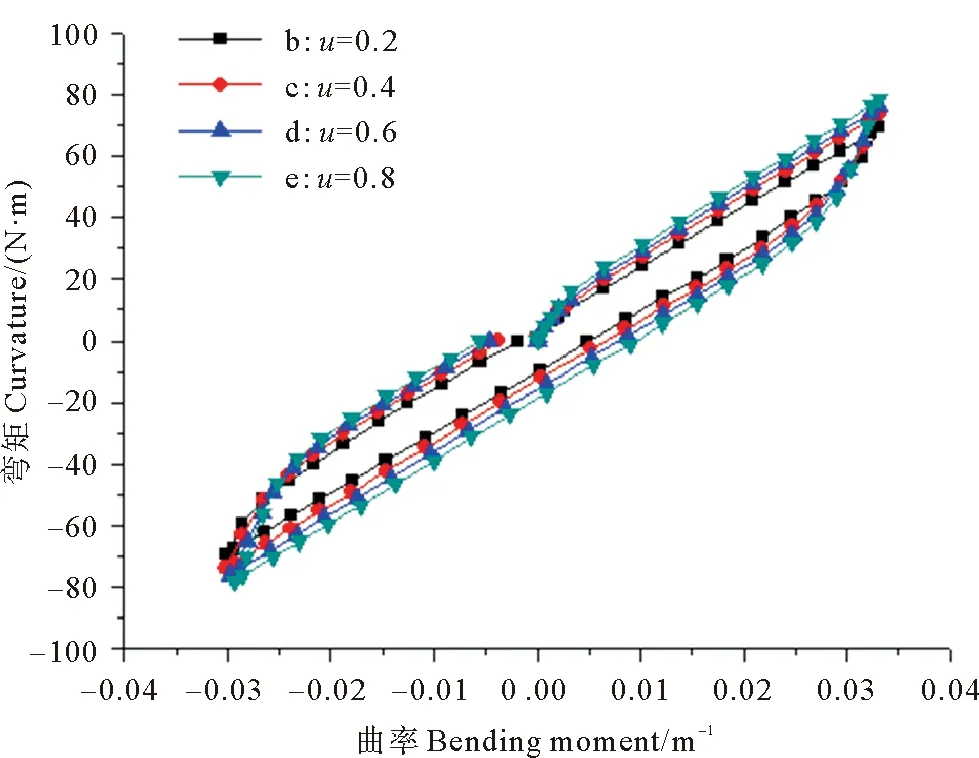
图5 不同摩擦系数下弯矩—曲率曲线

由图5可知，当转角设置为0.02时，b、c、d和e曲线有明显的前滑移阶段、全滑移阶段和滞回阶段，正向加卸载全滑动阶段和反向加载卸载全滑动阶段的弯曲刚度接近。随u取值的增大，前滑移阶段持续时间有一定程度的增大，全滑移阶段和滞回阶段弯曲刚度增加，滞回曲线的面积也增大，说明摩擦耗能也越多。

不同摩擦系数下脐带缆全滑移阶段和滞回阶段弯曲刚度具体值如表3。该具体值取各阶段所有取值点斜率平均值。由表可见，弯曲刚度变化率基本稳定于120%附近。

表3 不同摩擦系数下各阶段弯曲刚度

3.2 外压对弯曲滞回的影响

脐带缆在制作过程中由于内部构件排布较为紧密，往往会产生内部的预压力，由此增大的摩擦影响带来了弯曲刚度的增加。因此外压敏感性分析具有重要意义。考虑外压大小分别为0、0.25、0.5和1 MPa，其在摩擦系数为0.4时的弯矩曲率变化曲线如下：

从图6中可以看出，随外压的增大前滑移阶段持续时间和弯矩滞后于曲率现象持续时间明显增加，前者是由于外压增强了结构的抗滑移能力，进而延后了滑移点出现的时间，后者则是由于正向卸载时，较大的层间摩擦可以更好地阻止反向滑移的产生。全滑移阶段和滞回阶段弯曲刚度增加，且正向与反向变化规律一致，曲线更加饱满，滞回曲线所包含面积有明显增加。

图6 摩擦系数为0.4时不同外压作用弯矩—曲率曲线Fig.6 Moment-curvature relationship under different external press

正向全滑移阶段与滞回阶段弯曲刚度变化如图7。随外压增大，两阶段刚度差值基本稳定，虽然弯曲刚度增加，但增加幅度逐渐放缓。

图7 不同外压下全滑移阶段与滞回阶段弯曲刚度变

3.3 螺旋角度对弯曲滞回的影响

螺旋角度也是脐带缆重要的设计参数之一。选取摩擦系数为0.6，脐带缆的螺旋角度分别为8°、10°、12°、14°和16°，探究螺旋角度对弯曲滞回的影响。

由图8可知，随螺旋角度增大，有限元模拟出的全滑动和滞回阶段的弯曲刚度逐渐减小。相比于全滑动阶段，滞回阶段刚度变化幅度更大。下图9分别为螺旋角度为8°、10°、12°和14°时的mises应力云图。图中应力较大位置基本集中于脐带缆内部钢管单元上下管壁处，随螺旋角度的增大，电缆和光纤单元内部应力明显增大。

图8 不同螺旋角度全滑移阶段与滞回阶段弯曲刚度

图9 螺旋角度为8°、10°、12°、14°时应力图

3.4 填充单元对弯曲滞回的影响

在对脐带缆结构进行数值模拟分析时，由于填充部分较整体来讲刚度较小，因此为了简化模型，多不考虑填充单元的影响。但考虑到本文所研究的脐带缆弯曲迟滞现象的产生是基于内部构件间的摩擦滑移，而填充单元的存在增大了构件间的接触面积，使得脐带缆的滑移行为更加复杂。所以填充单元的存在也会对脐带缆的弯曲滞回具有一定影响。本文考虑如图10所示部分填充和密实填充两种情况，就填充单元对脐带缆的弯曲刚度影响程度进行探讨，其中填充单元材料是聚合物材料。

图10 部分填充和密实填充钢管脐带缆有限元模型

由图11、12可知，不同摩擦系数下含填充的脐带缆的正向全滑移阶段弯曲刚度略大于不含填充的脐带缆，而滞回阶段弯曲刚度当摩擦系数较小时两者基本一致，随着摩擦系数的增大前者略大于后者。经分析可知，填充单元表面粗糙程度越大其对滞回阶段刚度影响的程度越大，当摩擦系数取0.8时差值约为0.9%，在工程可接受的范围内。因此在精度允许的情况下，也可不考虑填充单元的影响。

图11 不同摩擦系数下不含填充与部分填充全滑移阶段与滞回阶段弯曲刚度变化

图12 不同摩擦系数下部分填充与密实填充全滑移阶段与滞回阶段弯曲刚度变化

4 结论

本文基于ABAQUS软件，建立非粘结钢管脐带缆模型，通过分析摩擦系数、外压大小、螺旋角度等参数以及填充单元对某工程实例中的脐带缆弯曲滞回现象的影响，得到以下结论：

(1)随摩擦系数u取值的增大，非粘结钢管脐带缆前滑移阶段持续时间增加，全滑移阶段和滞回阶段弯曲刚度增加，滞回曲线面积随之增大，摩擦耗能越多。全滑移阶段和滞回阶段之间的弯曲刚度变化率基本稳定于120%附近。

(2)随外压大小的增大，非粘结钢管脐带缆前滑移阶段持续时间和滞回阶段持续时间明显增加，前者是由于外压的存在使得结构更密实，抗滑移能力增强进而延后了滑移点出现的时间，后者则是由于正向卸载时，较大的层间摩擦可以更好的阻止反向滑移的产生。全滑移阶段和滞回阶段弯曲刚度增加，滞回曲线所包含面积有明显增加。

(3)随螺旋角度增大，有限元模拟出的全滑动和滞回阶段的弯曲刚度逐渐减小。且相比于全滑动阶段，滞回阶段的刚度减小趋势更为明显

(4)填充单元对滞回刚度的影响程度随摩擦系数的增大而增大，在u较小时填充单元对滞回阶段弯曲刚度影响可忽略不计，在u较大时差值也都在工程可接受的范围内。

综上所述，在进行非粘结钢管脐带缆弯曲滞回性能的数值模拟时，为了得到较为精确的各阶段弯曲刚度变化规律，摩擦系数、外压大小、螺旋角度以及填充单元均是需要深入探讨的问题。