单气泡上升对近壁面传热影响的数值研究
张文峰,庞明军
(常州大学机械与轨道交通学院,江苏 常州 213164)
泡状流动(或气泡在液相中的运动)广泛存在于在自然界和工业过程中,如岩浆流动、金属冶炼、石油输送等过程.气泡的存在有助于液相内(或固壁)热量的传输和扩散,均匀温度场的分布,起到强化传热的作用[1-3],从而实现节能减排的目的.文献研究表明,当有小气泡出现在加热壁面时,局部传热系数可提高2倍~3倍[4].因此,为了理解气泡对不同泡状设施内固壁和液相间的传热影响规律和影响机理,国外学者相继开展了相关研究.
理论上,Deckwer[1]推导出鼓泡塔反应器的理论传热方程,揭示了传热系数对气泡的依赖关系.Khabeev[5]提出了一种描述气泡与液相间的传热方法,并导出气泡边界处的热流表达式.数值上,Larimi和Ramiar[6]用流体体积法(VOF)研究了管道内静止和非静止液体内单气泡上升对努塞尔数的影响.他们发现,当液相的雷诺数较高时,气泡上升对努塞尔数没有明显的影响;而当液相的雷诺数较低时,气泡上升对努塞尔数有显著的增强作用.Deen和Kuipers[7]使用VOF方法研究了气泡在热壁附近上升对固壁与液相传热系数的影响,发现由于气泡对流体的扰动,特别是在热壁附近有气泡合并时,壁面与液体间的传热系数显著提高.Bhuvankar和Dabiri[8]使用前沿跟踪法(FT)计算了单气泡在剪切流中上升时对固壁面和液相间传热的影响;结果表明,在气泡的下游和上游区域,传热表现出强化和减弱的现象.实验上,Donoghue和Delaure[9]研究了单个气泡撞击热水平壁面的传热现象,发现与单纯的自然对流相比,反弹气泡显著增强了水平壁面的传热系数.在随后的研究中,他们还发现,单个气泡撞击加热水平壁面时,在气泡影响区域和其尾流区域内,对流传热的变化在空间上是对称的,并且气泡附近的热通量呈现出大幅、快速波动的现象[10].Qiu和Dhir[11]研究了气泡沿倾斜加热壁面上滑时的流动模式和传热现象,发现上滑气泡尾流区的传热得到了显著强化.
虽然国内外学者对此类课题已经展开了一定的研究,但是气泡传热强化的机理尚不明确.因此,探究气泡上升对传热的影响规律和强化机理对于泡状设施的设计和控制具有重要意义.本文利用VOF法,详细研究了表面张力、重力水平和气泡距固壁距离对单气泡上升固壁与液相间传热的影响规律,以获得一些潜在的机理解释.
1 物理模型和工况设置
为了研究气泡上升对固壁与液相间传热的影响,几何模型如图1所示.为了简化计算,将计算模型简化为二维平面模型.为使气泡的运动在计算域内能达到稳定运动状态,且避免左壁AC对气泡变形和运动的影响,故计算区域的尺寸设置为,高H=50d、宽L=(40/3)d.气泡圆心距右壁BD的距离为l=1.5d和2.5d,距CD为h=(17/6)d.d为气泡的初始直径,d=6 mm.
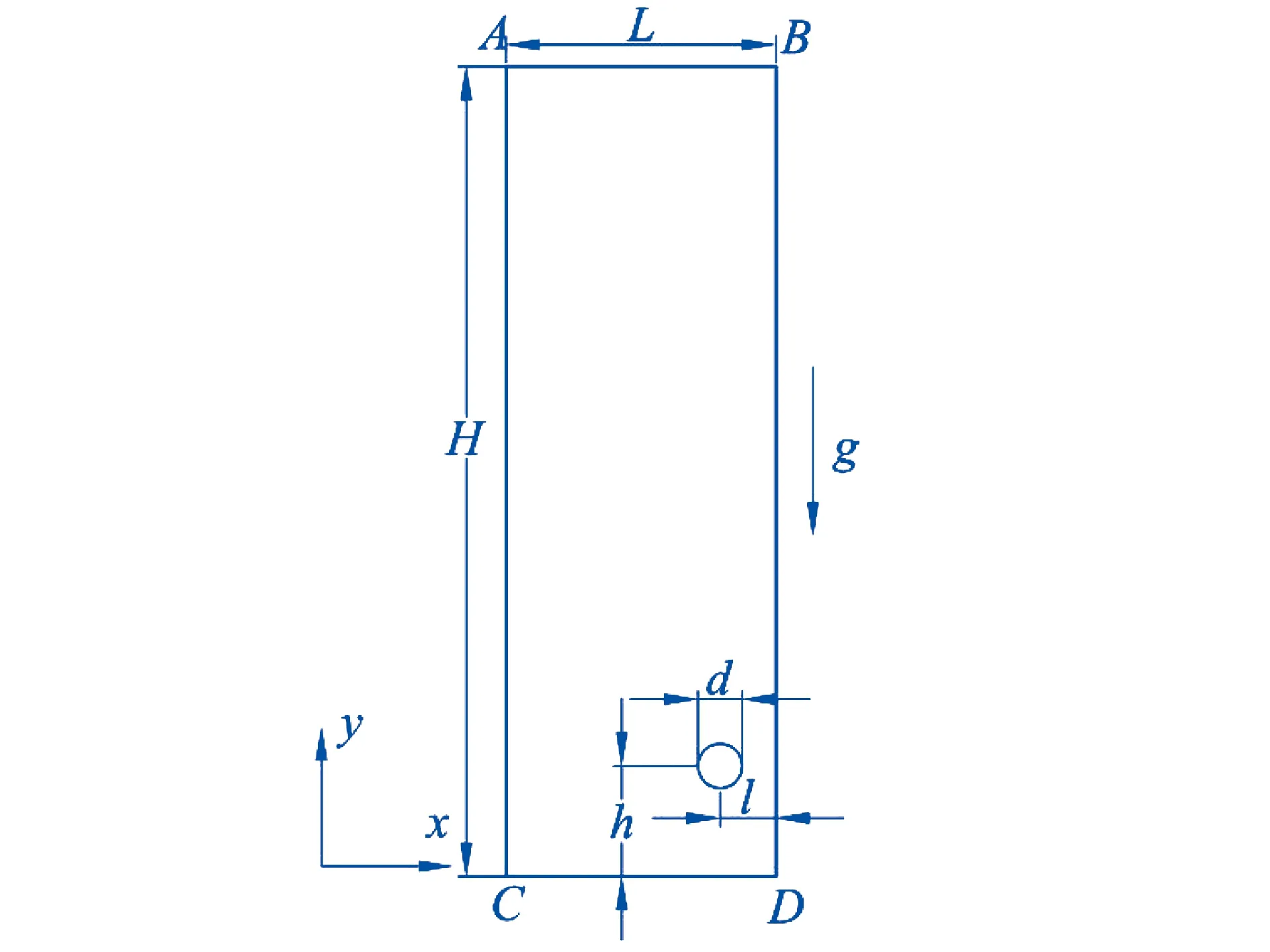
图1 计算区域
计算时,对于流动而言,将AB、AC、CD和BD均设置为无滑移壁面,重力沿着y轴负方向;对于传热而言,分别在BD和AC施加393 K和293 K的壁面温度,AB、CD设置为绝热边界条件.另外初始状态下的气相和液相都是静止的,温度均为293 K.
气泡在静止液体内上升时,主要受重力、黏性力和表面张力的影响,这三种力可由无量纲参数Eötvös(Eo)数和Gallilei(Ga)数表示.Eo数是重力和表面张力的比值,Ga数是重力和粘性力的比值,其定义式见公式(1)和公式(2).通过改变表面张力、重力水平和气泡距固壁的距离,分别控制Eo数、Ga数和l,来改变气泡运动状态,从而研究气泡对壁面对流传热的影响.因此,设计了三组工况:(1)Eo=1、5、20和80时,Ga=14.5(1g),l=1.5d;(2)Ga=14.5(1g)、12.6(0.75g)和10.3(0.5g)时,Eo=5、20和80,l=1.5d;(3)l=1.5d和2.5d时,Eo=5和80,Ga=14.5(1g).
(1)
(2)
公式中:ρl为液相密度,kg/m3;g为重力加速度,m/s2;d为气泡直径,m;μg为液相黏度,Pa·s;σ为表面张力,N/m.本文计算工况的物性参数,如表1所示.
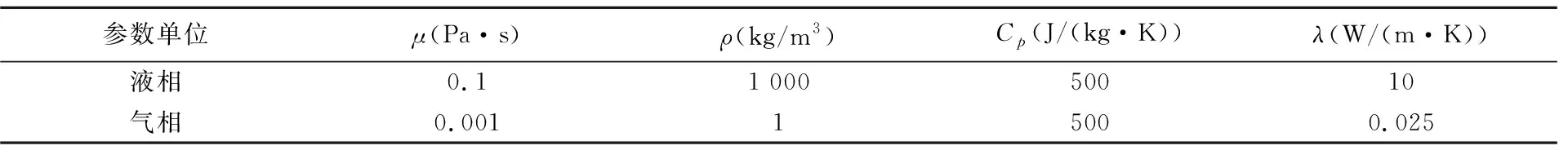
表1 气液物性参数
2 控制方程和数值方法
2.1 控制方程
计算时候假设液相和气相都是不可压缩流体,且流动近似为层流,液相和气相的控制方程如下.
连续性方程:
∇·u=0,
(3)
动量方程:
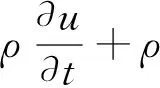
(4)
公式中:u为速度矢量,m/s;ρ为流体局部平均密度,kg/m3;μ为流体局部平均黏度,Pa·s;p为压力,Pa;Fσ为由表面张力引起的体积力,N;∇为哈密顿算子.
流体的局部平均密度和粘度分别按下式进行计算:
μ(f)=μ1(f)+μg(1-f),
(5)
ρ(f)=ρ1(f)+ρg(1-f),
(6)
公式中:下标g和l分别为气相和液相,后文与此相同.
为了得到温度场,忽略黏性耗散的影响,能量守恒方程可写为

(7)
体积热容ρCp和局部平均热导率λ分别用下面的式子计算:
ρCp(f)=ρlCp,l(f)+(1-f)ρgCp,g,
(8)
λ(f)=λl(f)+λg(1-f)
.
(9)
2.2 VOF方法
为了精确捕捉气液两相的界面变化,故采用计算精度高计算速度快的VOF法.VOF法的相函数输送方程为
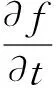
(10)
相函数f可定义为

(11)
得知相函数,可利用公式(12)计算气泡的局部体积分数:
(12)
公式中:s为网格编号;AS编号为s网格单元的面积.界面的重构利用分段线性法(PLIC),该方法使用直线段近似表示单个网格内气液两相的界面.界面法向量通过求解网格单元中气泡的局部体积分数梯度来获得,界面的法向量n表示为
(13)
2.3 连续表面张力模型
Brackbill等[12]所提出的连续表面张力模型被用来计算表面张力.在计算过程中,表面张力作为源项体积力Fσ出现在动量方程的右边,即
Fσ=σκδn,
(14)
公式中:δ为狄拉克分布函数;κ为相界面曲率,即
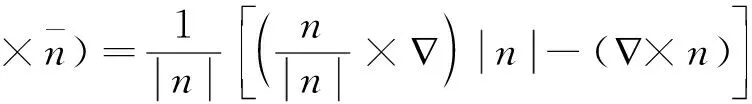
(15)
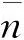
2.4 网格划分
因结构性网格生成速度快,网格质量好,数据结构简单[13],所以网格划分采用正方形结构性网格.为了获得较高精确的计算结果、并且降低计算成本,同时在气泡周围采用了自适应网格法(AMR).自适应网格生成时,把气相体积分数作为变量,对气液交界面处的网格进行加密,即在气相体积分数大于0且小于1时的网格,进行局部加密,网格划分如图2所示.

图2 网格划分
2.5 数值方法
计算采用非稳态的层流模型,速度和压力场耦合采用PISO算法,选用最小二乘法离散单元中心的变量梯度,压力项选用PRESTO格式离散,动量和能量方程选用二阶迎风格式进行离散.压力、动量、体积力和能量的亚松弛因子分别设为 0.3、0.7、1和1,时间步长设置为5×10-5s,以保证较好的收敛性和稳定性.计算时先进行初始化,使计算域内充满静止液体,然后再把直径为d的气泡放到指定位置,进行两相流计算.
3 网格无关性和结果准确性验证
3.1 网格无关性验证
为了保证网格尺寸不对计算结果产生影响同时又能降低计算量,采用三种不同的网格对最复杂工况(Eo=80和Ga=14.5)的计算结果进行了检验.自适应网格的初始尺寸都是d/6,初始网格数均为96000.为了减少计算量,采用了自适应网格划分技术.即在计算过程中,对气液界面所临近的网格进行了局部加密.分别尝试加密了4次(Grid1)、3次(Grid2)和2次(Grid3),得到气液界面位置处最小的网格尺寸分别是0.375/d、0.75/d、1.5/d.三种网格下气泡速度随时间的变化如图3所示,可以看出Grid1和Grid2的计算结果基本一致.结合计算量和准确性的考虑,最终选择Grid2网格系统进行计算.
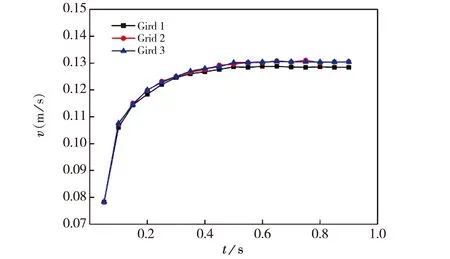
图3 三种网格系统的气泡速度对比
3.2 结果准确性验证
为了描述壁面传热效果的好坏,给出了对流传热系数的定义:
(16)
公式中:αw为存在气泡上升工况的局部传热系数;T1为热壁面温度;T0为流体的平均温度.
因努塞尔数可以表征对流传热的强度,下面给出有气泡上升时壁面局部瞬时努塞尔数Nu的定义式:
(17)
公式中:L为模型的宽度,m;λ1为液相的热导率,W/(m·K).
为了验证计算方法的可靠性,把相似工况的计算结果和文献[14]的结果进行了对比,如图4所示.可见,椭圆形气泡在固壁附近上升时的Nu随计算时间的变化为一条平滑的曲线,努塞尔数随计算时间的增加逐渐减小、最后趋于一个稳定的值,这与文献[14]得到的结果一致.
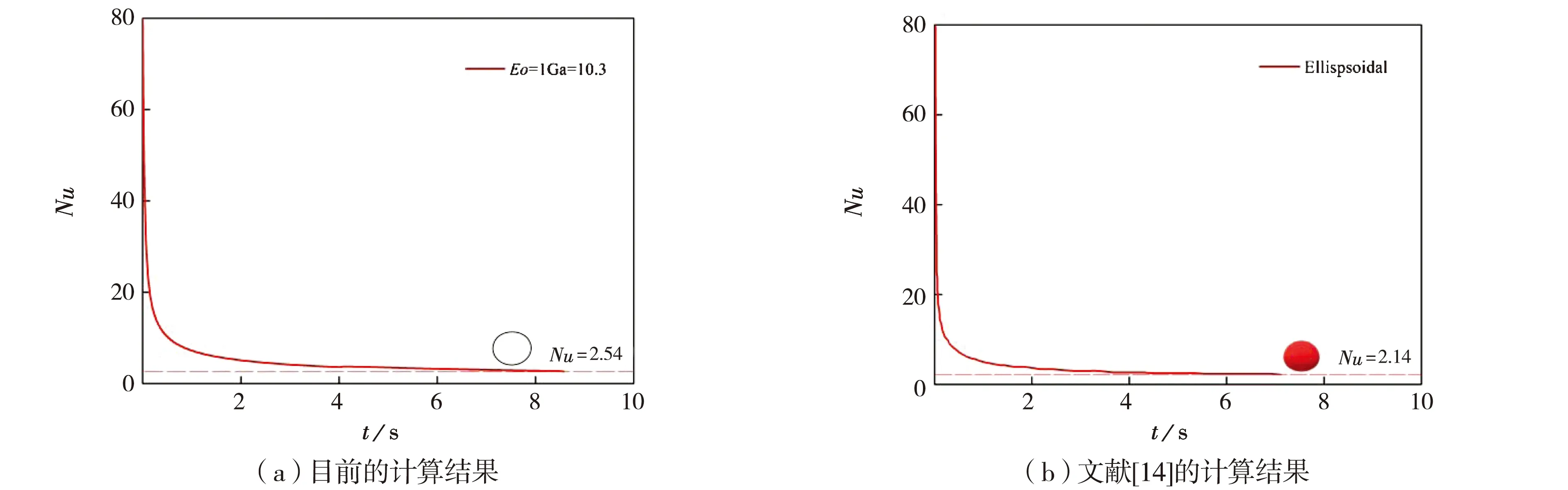
图4 本文计算结果和文献[14]对比
4 结果分析和讨论
为了便于对比分析,定义了局部瞬时无量纲壁面努塞尔数
(18)
公式中:Nuz为没有气泡上升时壁面的瞬时努塞尔数.
4.1 气泡上升对壁面传热的影响
4.1.1 不同Eo数下气泡对壁面传热的影响
首先研究了给定重力水平Ga=14.5(g)和壁面距离l=1.5d下,表面张力对传热的影响.根据公式(1)可知,表面张力的影响可用Eo数表征.在给定重力水平Ga=14.5(g)下,不同Eo数所对应的气泡形状如图5(a)所示.可见,Eo数越大、气泡形变越厉害,和文献[15]的计算结果基本吻合.
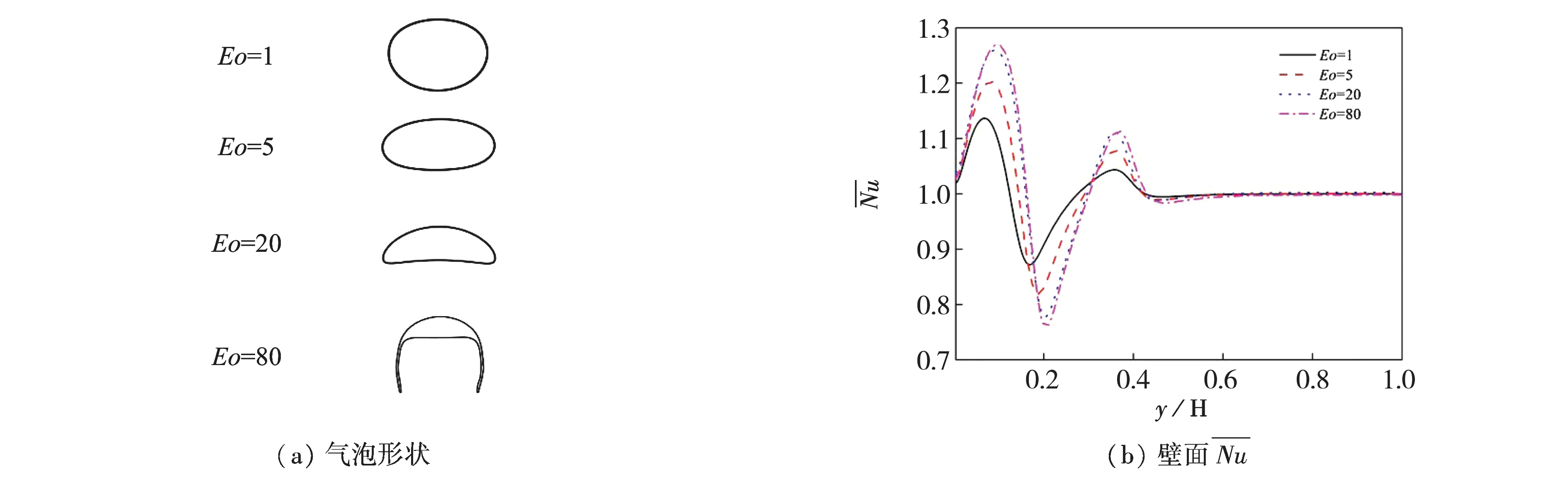
图5 不同Eo数下气泡形状及对应的
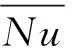
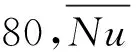
4.1.2 不同Ga数下气泡对壁面传热的影响
其次,在给定的Eo数和壁面距离l=1.5d下,研究了重力水平(即Ga数)对壁面传热能力的影响.常重力1 g对应的Ga=14.5,0.75 g对应的Ga=12.6,0.5 g对应的Ga=10.3.
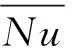
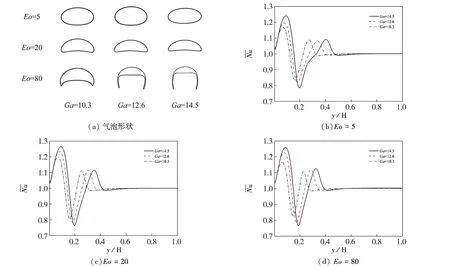
图6 不同Ga数下气泡形状及对应的
对于相同的Eo数,尽管重力水平(即Ga数)对气泡的形状影响不大,但会对气泡的上升速度产生重要影响.重力水平越高(即Ga数越大),相同形状气泡的上升速度越大,其对气泡上升经过的流场扰动越大,导致传热强化区的范围越宽,第一峰值也越大.第二峰值位置的偏移,是因为相同时间下,不同Ga数下气泡上升的位置不同造成的;其小基本没发生变化,是因为气泡的形状和横向尺寸变化轻微,不足以引起气泡热壁面一侧的流场发生明显的变化.
4.1.3 气泡不同初始位置对传热的影响
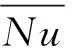
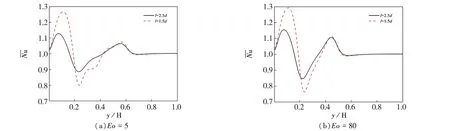
图7 气泡不同初始位置l对壁面的影响(Ga=14.5)
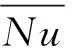

图8 气泡上升过程对壁面的影响
另外,从图8也可以看出,第二峰值所对应的气泡方位是变化的.当计算时间为0.1 s时,第二峰值对应气泡的赤道位置;在0.2 s时,对应气泡的底部;随着气泡上升距壁面距离的增大,其逐渐下移到气泡的下游位置;当计算时间大于0.6 s时,气泡上升过程趋于稳定、距壁面的距离不再增大,此时第二峰值所对应的气泡方位也趋于稳定,第二峰值的大小也不再变化.这是因为气泡对流场的扰动需要更长的时间才能对热壁面附近的对流传热产生影响,即流动和传热之间存在滞后效应[14].
4.2 传热强化机理分析
为了理解气泡加入后对传热的影响机理,下面分别分析了气泡加入后对温度场和流场的影响.
4.2.1 气泡上升对温度场的影响
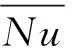
从图9可以看出,当气泡的Eo数不同时,气泡对热边界层的影响程度是不同的.为了更好地比较热边界层厚度的变化,图10给出了热边界层最薄处沿横向的温度分布.从图10可以看出,随着Eo的增大,温度开始变化的位置越来越靠近热壁面,这说明热边界层逐渐变薄;还观察到Eo=20和Eo=80的曲线十分相似,即它们的热边界层厚度十分接近.热边界层厚度的关系和4.1.1节中得出的结论一致:Eo数越大,气泡引起的热边界层越薄,所引起的传热强化程度越显著.
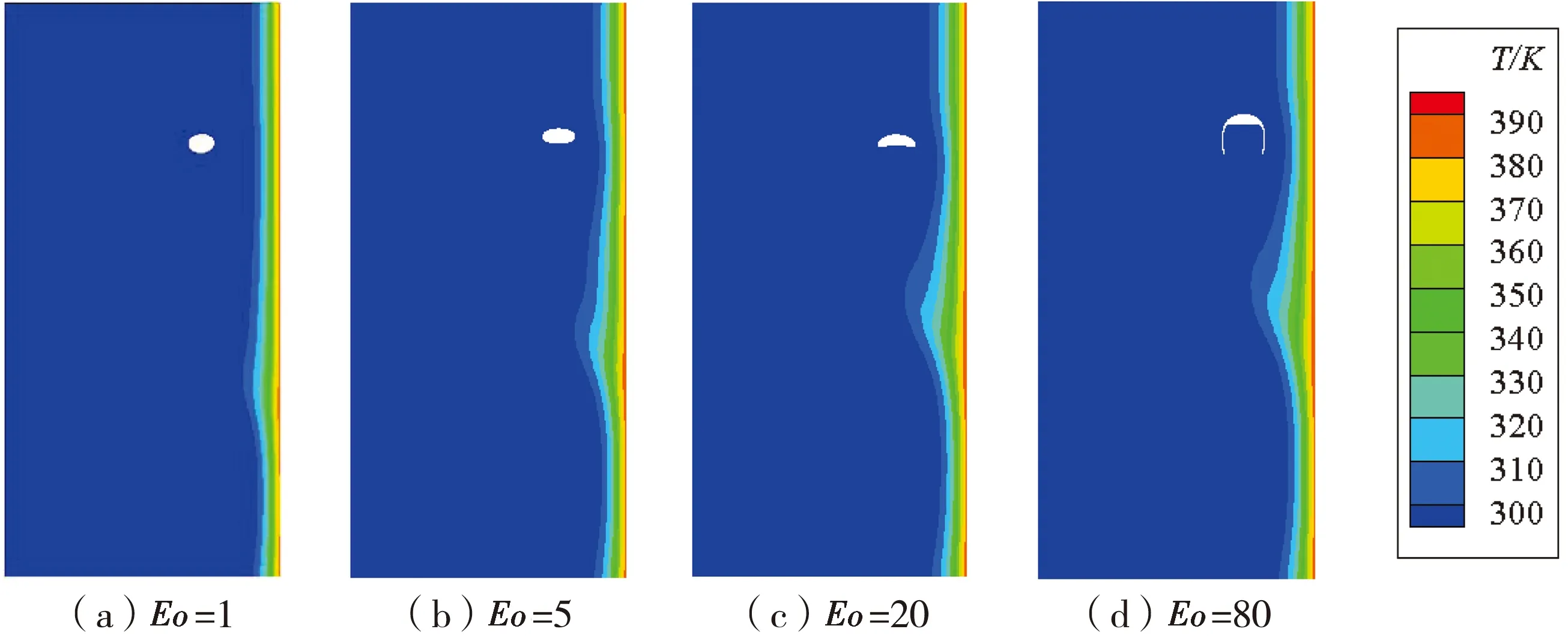
图9 不同Eo数下气泡周围的温度场
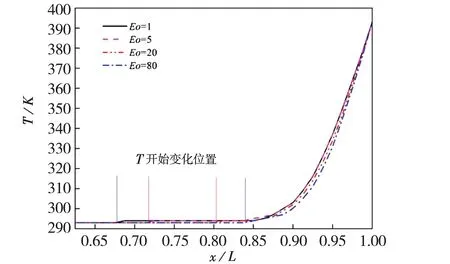
图10 最薄热边界层处,温度沿x方向的变化
4.2.2 气泡上升对速度场的影响
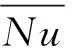
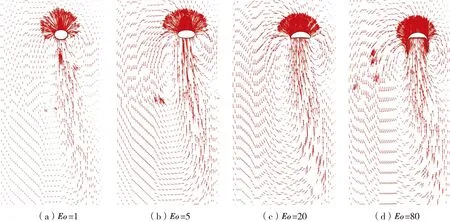
图11 不同Eo数下流场的速度矢量图
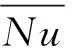
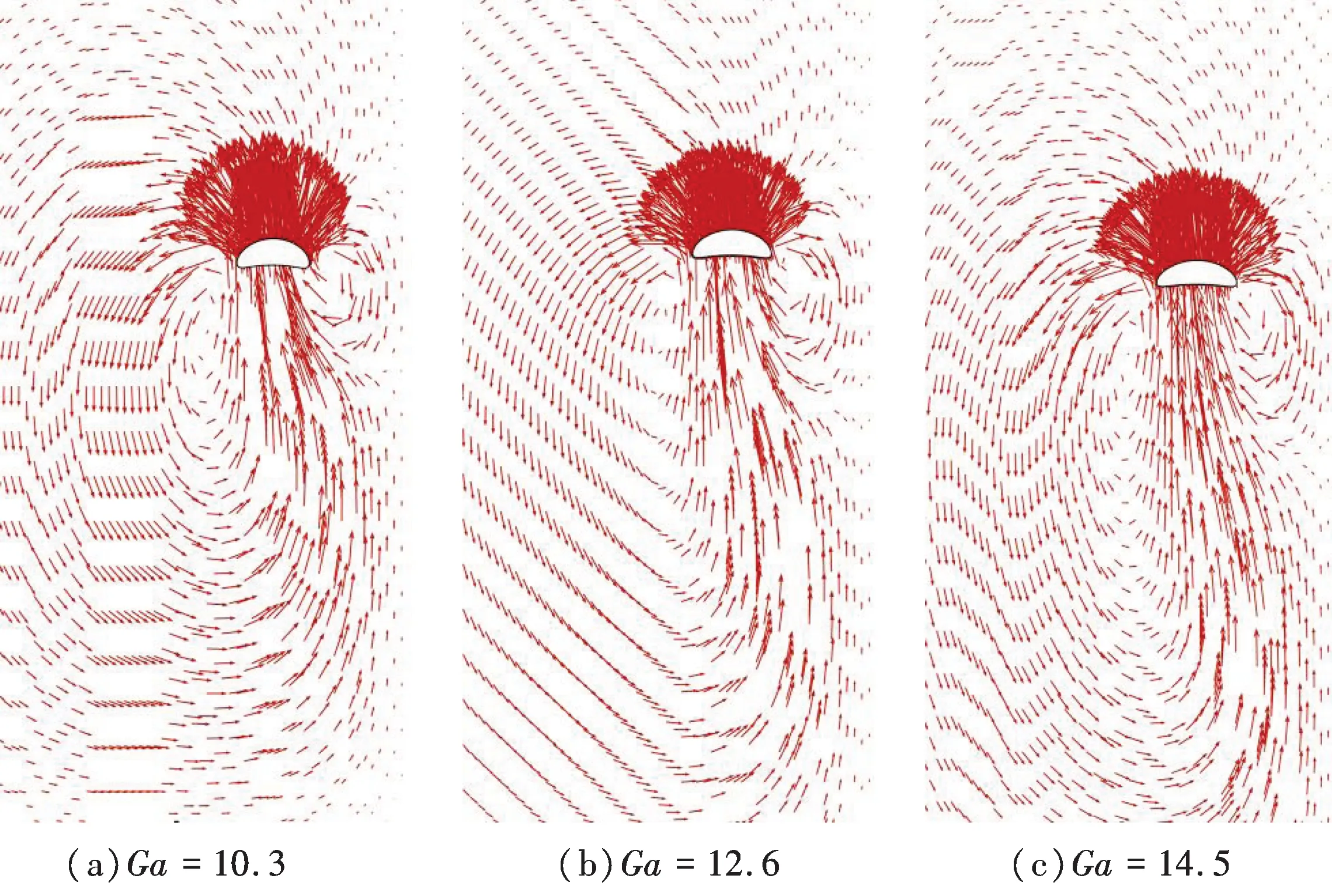
图12 不同Ga数下流场的速度矢量图
图13给出Eo=80和Ga=14.5(1 g)时,不同气泡初始位置(l)下气泡的速度矢量图.气泡初始位置的改变,和重力水平类似,影响的是气泡初始位置附近的流动状况.l=1.5d工况气泡左侧涡的强度比l=2.5d工况的强;同样气泡右侧涡的强度变化不大.这也符合4.1.3节得出的结论,气泡距离热壁面的距离越小,对流体的扰动越大,气泡初始位置附近的传热强化程度也就越显著,但对气泡位置附近的传热强化程度影响甚微.
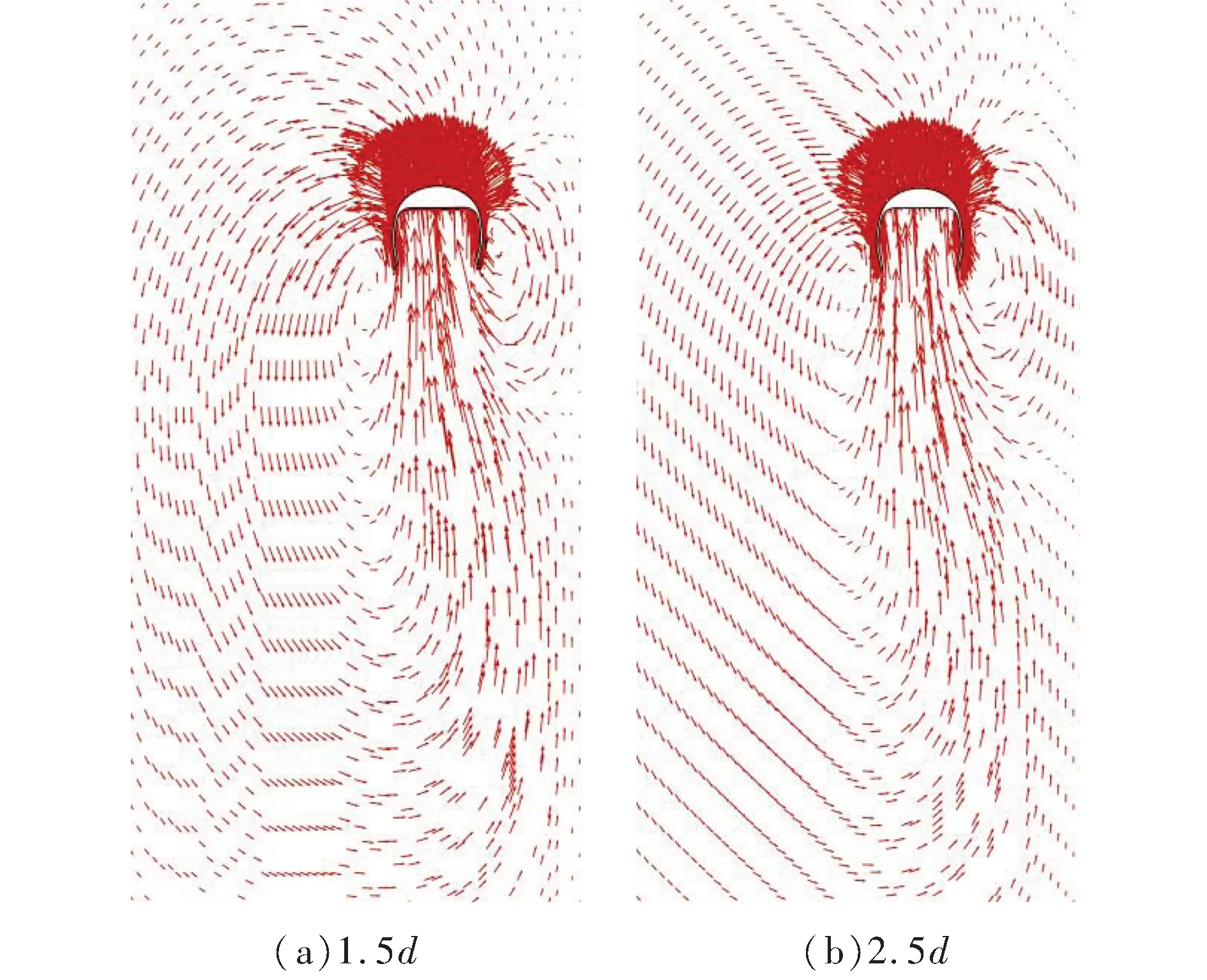
图13 气泡不同初始位置对应的流场速度矢量图
综上分析,气泡之所以能改变壁面附近流体的对流传热效果是因为气泡在近壁面上升时改变了近壁面区域的流场分布,形成旋向相反、尺度不同的对涡,改变气泡附近和其所过区域流体的流动状况,引起近壁热边界层厚度的变化,从而改变了近壁面流体的对流换热效果.
5 结 论
本文采用VOF法研究了静止液体中单气泡上升对近壁面传热的影响,详细研究了表面张力、重力水平和气泡初始位置对热壁面附近对流传热程度的影响.可以总结出如下几点结论:
(1)Eo数越大,气泡的横向尺寸越大,其上升过程对流体的扰动越大,因此对流传热强化效果越好;
(2)气泡形状一定时,重力水平(即Ga)越大,气泡上升过程对流体的扰动越大,导致气泡初始位置附近区域的对流传热强化效果越好;
(3)气泡的起始位置主要影响初始位置附近处的对流传热程度,气泡距热壁面越近,初始位置处的传热强化效果越好;
(4)气泡上升过程产生旋向相反的对涡影响了冷热流体的流动状态,从而引起热边界层厚度的变化,最终改变了壁面附近流体的对流传热效果.

