低渗透各向异性油藏菱形井网储量动用评价及设计优化

陈民锋，杨子由，秦立峰，付世雄，荣金曦

[1.油气资源与探测国家重点实验室 中国石油大学(北京)，北京 102249； 2.中国石油大学(北京) 石油工程学院，北京 102249； 3.中海石油(中国)有限公司 天津分公司 渤海石油研究院，天津 300459]

中国有储量丰富的低渗透油藏，根据渗透率大小可划分为常规低渗透、特低渗和超低渗油藏等类型。由于启动压力梯度的影响存在一定的滞留区，此类油藏渗流阻力较大。此外，由于油藏储层物性变化以及天然和人工裂缝的影响，油藏平面不同方向上的渗透率存在较大差异，即渗透率各向异性明显。因此，低渗透各向异性油藏在开发过程中，常表现出储量动用难度大、动用程度低、注水沿主渗流方向突进以及平面驱替不均衡的特点，导致注水开发效果较差[1-8]。此类油藏在实际开发中，初期一般采取菱形注采形式的基础井网，其中开发井距和井排比的优化配置是井网部署成功的关键。

针对低渗透各向异性油藏的开发规律，以及合理开发、菱形井网的优化设计问题，大部分学者运用油藏数值模拟和理论计算等方法，通过对产油量、含水率变化和稳产时间等为优化目标进行分析[9-20]；较少根据开发井网注采单元的渗流场分布变化，对注采单元中的储量动用以及注水驱替均衡性等方面进行论证；关于合理注采井距、井排比的确定，一般采取单因素对开发效果影响的优化分析方法[21-28]，而通过分析各因素对油藏储量动用效果和均衡驱替的影响，并考虑多因素交叉干扰条件下，实现合理井距和最佳井排比的联立优化求解的相关研究较少。

对于一般低渗透油藏(渗透率在10×10-3～50×10-3μm2)，具有一定的自然产能，油藏整体表现出孔隙渗流的特征，但储层具有一定启动压力梯度和较为明显的各向异性。此类油藏储量丰富，大量开发实践表明，采用合理的菱形井网是油藏开发成功的基础。本文基于实际低渗透各向异性油田开发的典型井网形式，应用经典渗流力学理论，研究不同因素影响下菱形井网中储量有效动用规律和均衡驱替效果，建立同时实现“储量有效动用程度满足油田开发要求、注采均衡驱替效果好”的菱形注采井网优化模型，为此类油藏的有效开发提供科学依据。

1 低渗透各向异性油藏菱形井网渗流方程及其求解

针对典型的低渗透油藏地质和开发条件，分析储层启动压力梯度和渗透率各向异性影响下的渗流方程，建立菱形井网形式下注采单元的渗流模型，并求解计算渗流场分布。

1.1 低渗透各向异性油藏适宜井网形式

菱形井网是矢量井网的一种特殊形式，矢量井网通过控制注采井距提高储量动用程度，变化注采形式和调整井排比，特别适用于非均质性较强、主渗流方向明显的油藏。矢量井网形式一般有：矩形反五点法、矩形线性(排状)、矩形反七点法和菱形反九点法。

由于初期油井井数多，菱形反九点法井网更适合油藏开发初期的需求，沿主渗流方向上注采井距长、垂直主渗流方向上井排距离短，易于获得在各个方向上相对均衡的驱替效果；在开发中后期不增加井数的情况下，可以根据需要调整为矩形反五点法井网，或矩形线性(排状)井网。

中国大多数低渗透油藏的开发实践表明，菱形反九点法井网适合作为低渗透各向异性油藏开发的基础井网。因此，适合目标油藏条件、满足油田开发需求的菱形井网关键技术参数——合理井距、最佳井排比的确定，是油藏注采井网部署的关键。

1.2 低渗透各向异性菱形井网渗流方程及其求解

1.2.1 菱形反九点井网基本形式

典型的菱形反九点法井网如图1所示。在所研究的一个完整的注采单元中，有1口中心注水井和8口生产井。其中井距dS为相同井排中两井之间的距离，m；排距dR为相邻两个井排之间的垂直距离，m；井排比为井距与排距的比值，为ε=dS/dR，无量纲。

对于低渗透各向异性油藏，在确定条件下，通过“缩小井距”增大驱动压力梯度，来提高注采单元中储量的有效动用程度，通过“控制井排比”，来实现各个方向上的均衡驱替。基于该典型井网形式，考虑渗透率各向异性以及启动压力梯度的影响，利用渗流力学势的叠加原理，建立针对性的菱形注采井网渗流模型，研究不同条件下注采单元中平面渗流场变化规律，为实际油藏开发井网设计优化奠定理论基础。

图1 菱形反九点基本井网形式示意图Fig.1 Schematic diagram showing the rhomboid inverted nine-point well pattern(xt，yt为流体分别沿x，y方向流动时在某时刻到达的位置，m；Kx，Ky分别为沿x，y方向的渗透率，10-3 μm2；dS为井距，m；dR为排距，m。)

1.2.2 菱形反九点井网渗流方程的建立

1) 基本渗流模型

在常规油藏中，平面渗流基本微分方程为：

(1)

式中：p为压力，MPa；x为沿渗流主方向的距离，m；y为沿垂直渗流主方向的距离，m。

若油藏中所有井定产生产，则根据叠加原理可知，平面中某一点的压力为：

(2)

式中：m为井数，口；pi为某井在任意点处产生的压力，MPa；C为常数，无量纲；μ为地层原油粘度，mPa·s；K为油藏渗透率，10-3μm2；h为油藏有效厚度，m；qi为油井产液量或注水井注入量，m3/d；ri为任意点距某井的距离，m。

根据压力分布表达式，可以求出速度分布表达式：

(3)

式中：v为某一点速度，m/d。

2) 考虑启动压力梯度和各向异性影响的渗流模型

相关研究结果表明，储层启动压力梯度G与流度λ=K/μ之间满足对数关系，可表示为[29]：

lnG=Alnλ+B

(4)

式中：G为储层启动压力梯度，MPa/m；λ为流体流度，10-3μm2/(mPa·s)。对于本文研究油藏，A=-0.75，B=-3.76。

在各向异性油藏中，流体在不同方向的渗流能力存在差异，其渗流阻力各不相同，因此各方向上的启动压力梯度也不同，可以得到不同方向上的渗流速度基本表达式：

(5)

式中：vx，vy分别为沿x，y方向渗流速度，m/d；Kx，Ky分别为沿x，y方向渗透率，10-3μm2；Gx，Gy分别为储层在x，y方向上的启动压力梯度，MPa/m。

在各向异性油藏中，假定主渗流方向为x轴方向，y轴方向上渗透率最小，可得连续性方程：

(6)

式中：ρ为流体密度，g/cm3。为简化上述渗流方程，通过坐标变换和等效处理，将原各向异性平面转化成各向同性平面，为此做出如下变换：

(7)

经过坐标变换，可得低渗透各向异性油藏的渗流方程为：

(8)

式中：X，Y分别为坐标变换后沿渗流主方向距离和垂直渗流主方向距离，m。

若无限大地层存在一口生产井，其产液量为q。在注采平面以该井轴为轴的圆柱面上，根据公式(10)可知，其半径为R，按照达西定律，可知通过井点的流体质量为：

(11)

式中：q为无限大地层存中一口生产井的产液量，m3/d；Rw为井筒半径，m；R为井的泄流半径，m。

在变换后的各向同性平面上，无限大地层中考虑启动压力梯度的渗流控制方程为：

(12)

1.2.3 菱形反九点井网注采单元平面渗流场求解

1) 压力分布

根据公式(12)所示的方程组，可求出地层中任一点的压力分布表达式：

(13)

当地层中有多口井同时生产时，根据叠加原理，可得注采单元中任一点的压力为：

(14)

式中：Δxi=x-xi，Δyi=y-yi分别表示注采单元中任意一点距某井在x，y方向上的距离，m。

2) 渗流速度

由于速度是矢量，可将任意点流体的速度在x，y方向上进行分解。在研究的注采单元中，多口井生产时某一点流体在x方向上的分速度为：

(15)

同理，多口井生产时某一点流体在y方向上的分速度为：

(16)

进而得到注采单元中某一点的渗流速度为：

(17)

式中：

基于低渗透各向异性油藏菱形井网典型形式(图1)，在注采单元整体保持注采平衡，利用公式(14)和(17)可分别求出任一点的压力和速度，即得到注采单元中渗流场分布。

1.3 菱形反九点井网渗流场分布规律

根据中国主要低渗透油田开发实践认识和本文研究油藏资料，确定了主要参数的取值范围(表1)。其中，平面渗透率级差JK反映油藏渗透率的各向异性程度，即

JK=Kx/Ky

(20)

启动压力梯度与流度λ相关，由公式(4)确定。

基于典型菱形反九点井网(图1)，设平行x方向为主渗流方向，当各参数取表1中的一般基准值时，计算得到注采单元中渗流场(包括压力场和速度场)分布(图2)。当各参数取不同值时，可以分析不同条件下渗流场分布变化规律(在注采单元渗流场中，黄色越深反映物理量的值越大，蓝色越深反映物理量的值越小)，进而得到不同因素对渗流场分布的影响。由图2可以看出：

表1 渗流场计算主要参数Table1 Main parameters applied for seepage field calculation

1) 对比有无启动压力梯度时，注采单元中压力场、速度场(变化形态和控制范围)差别明显。存在启动压力梯度时，渗流阻力更大，在相同注采压差条件下，注入端的高压区范围减小，采出端的低压区范围增大。井点附近的高速流动区范围减小，而井间低速流动区范围增大。

2) 当各向异性程度较大时，注采单元中x方向上阻力小、压力传播快，该方向的分速度大，压力和速度分布图中的等值线明显的扁平化，平行主渗流方向、垂直方向上的流动呈现驱替不均衡性。

3) 在不同地质条件下，注采单元中的低速流动区范围、驱替均衡程度不同，可以通过调整关键开发参数——井距和井排比，使得注采单元中低速流动区范围尽量小、驱替均衡程度尽量高。

4) 注采单元中的速度场分布，反映了不同位置处流体渗流速度的大小，流体速度越大表示该区域储量越容易动用。因此，可以利用注采单元中流体的渗流速度来反映流体(油相)动用的难易程度，进而表征储量的动用状况。

2 不同条件下菱形井网注采单元储量有效动用规律

对于低渗透各向异性油藏，进行菱形井网设计优化的目标，旨在实现油藏储量的有效动用和高效开发，即要求在整个注采单元中“低速流动区范围尽量小”，同时不同方向上的“驱替均衡程度尽量高”。因此，建立评价储量有效动用的指标和方法，并分析各因素对储量有效动用规律的影响，为低渗透各向异性油藏菱形井网设计优化奠定基础。

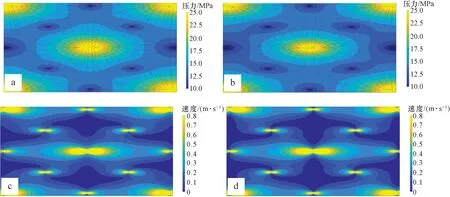
图2 不同条件下菱形反九点井网渗流场分布Fig.2 Seepage field distribution in rhomboid inverted nine-spot well pattern under different conditionsa. 不考虑启动压力梯度的压力场；b. 考虑启动压力梯度的压力场；c. 不考虑启动压力梯度的速度场；d. 考虑启动压力梯度的速度场

2.1 菱形井网注采单元有效动用评价方法

2.1.1 均衡驱替效果的评价方法

为反映注采单元中在平行主渗流方向、垂直主渗流方向上的驱替均衡程度，提出“均衡驱替系数”，来表征注采井网的均衡驱替效果。

在典型菱形反九点井网中，从注水井出发的速度等值变化范围(图1阴影处)。假设有两流体质点同时从注水井出发，分别沿x，y两方向流动，在某时刻分别到达xt和yt处。若要实现均衡驱替，距离xt和yt的比值应与注采井网的井排比尽可能相等，即有：

(21)

(22)

式中：tx，ty为流体分别沿x，y方向流动时的流动时间，d；vxa，vya为流体分别沿x，y方向流动时的流速，m/d；xt，yt为流体分别沿x，y方向流动时在某时刻到达的位置，m。

为便于在x，y方向上进行细分对比，可将不同方向上注采井间的距离均分成n个节点(n越大，在流动距离上的细分程度就越高，分析结果就越精确，本文取n=20)，对流体分别沿x，y方向上的速度在每对应节点处进行对比(图3)。

在图3中，灰色柱状长度表示流体质点分别沿x，y方向流动时在某对应节点处的速度差，该差距越小，表示流体各方向驱替均衡程度越高。为便于对比分析，将公式(22)带入公式(21)，得到两方向上“速度差”表达式：

(23)

若要最大限度地实现均衡驱替，就要使得流体质点在所有分析节点处、沿两方向的“速度差”趋于最小。定义“均衡驱替系数”的表达式为：

(24)

式中：σ为均衡驱替系数，无量纲；vxai，vyai为流体分别沿x，y方向流动时某节点处的流速，m/d；n为分析节点个数，无量纲。

当“均衡驱替系数”最大时，说明水驱开发的驱替均衡性更好，此时可以得到在给定条件下，满足油藏注采井网均衡驱替效果的最佳井排比。

图3 流体沿x，y方向流动时各节点处速度对比Fig.3 Comparison of velocities at each nodes when the fluid flows in the x and y directions

2.1.2 储量有效动用效果的评价方法

在给定的注采条件下，在注采单元中某些区域的驱替压力梯度小于或等于该处启动压力梯度时，导致该区域流体的渗流速度为0，则该区域的流体就不能动用。可将渗流速度为0的区域范围定义为无效动用范围，反之则为有效动用范围。

利用注采单元的“无因次有效动用范围”，来表征注采井网的储量有效动用效果，表达式为：

(25)

式中：ω为无因次有效动用范围，无量纲；SE为注采单元中的有效动用范围面积，m；ST为注采单元中研究范围的总面积，m2。若无因次有效动用范围越大，注采单元中渗流速度为0的范围越小，储量动用情况越好。

可以根据无因次有效动用范围的大小，表征注采单元中储量动用程度的高低。在确定的油藏条件下，要想达到某一储量动用程度水平，可以设定无因次有效动用范围的期望值，来求解相应的开发技术界限(如合理井距等)。

2.2 不同条件下均衡驱替变化规律

根据表1参数的取值，计算不同条件下菱形注采井网的渗流场分布，并统计得到不同因素影响下的均衡驱替系数变化曲线(图4)。

均衡驱替系数越大，注采单元中x方向与y方向上的驱替越均衡。均衡驱替系数最大时的井排比即为菱形井网最佳井排比。据图4可以看出：

1) 随注采压差、流度、渗透率级差、井距和井排比等因素取值的增大，均衡驱替系数一般呈现先增加后降低的规律，曲线极值点即对应该条件下的最佳井排比。

2) 当只考虑单因素变化的影响时，最佳井排比与流度、渗透率级差、井距呈非线性的正相关关系，与流度、注采压差呈非线性的负相关关系；而流度、注采压差和井距对最佳井排比的影响相对较小；渗透率级差对最佳井排比的影响相对较大。

3) 当综合考虑多因素变化的影响时，可以利用前述建立的理论方法，计算得到不同因素、不同取值水平组合下的结果，形成数据分析样本；再通过逐步回归分析法，得到菱形井网“均衡驱替系数”与不同影响因素之间的函数关系，作为低渗透各向异性油藏菱形井网设计的基础。

2.3 不同条件下有效动用范围变化规律

根据表1的参数取值，计算不同条件下菱形注采井网渗流场分布，并统计得到不同因素影响下的无因次有效动用范围的变化曲线(图5)。

无因次有效动用范围反映注采单元中能够流动的面积占单元控制面积的比，无因次有效动用范围越大，菱形井网注采单元中的储量动用程度越高。据图5可以看出：

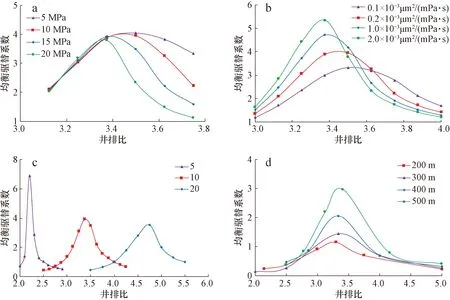
图4 不同条件下均衡驱替系数变化规律Fig.4 Variation rules of equilibrium displacement coefficients under different conditionsa. 不同注采压差；b. 不同流度；c. 不同渗透率级差；d. 不同井距

图5 不同条件下无因次有效动用范围变化规律Fig.5 Variation rules of dimensionless effective producing range under different conditionsa. 不同注采压差；b. 不同流度；c. 不同渗透率级差；d. 不同井排比

1) 随注采压差、流度、渗透率级差、井距和井排比等各影响因素取值的增大，无因次有效动用范围一般呈现单调递增或递减的变化规律。

2) 当只考虑单因素变化的影响时，无因次有效动用范围与注采压差、流度、井排比呈正相关关系，与渗透率级差、井距呈负相关关系。

3) 当综合考虑多因素变化的影响时，可以利用前述建立的理论方法，计算得到不同因素、不同取值水平组合下的结果，形成数据分析样本；再通过逐步回归分析法，得到菱形井网“无因次有效动用范围”与不同影响因素之间的函数关系，作为低渗透各向异性油藏菱形井网设计的基础。

3 基于储量有效动用的菱形井网优化设计方法

3.1 菱形井网优化设计方法和步骤

基于以上不同因素对低渗透各向异性油藏菱形井网渗流场分布规律的认识，建立菱形注采井网优化设计方法，详细步骤如下。

1) 基于菱形井网注采单元中的“均衡驱替系数、无因次有效动用范围”与不同影响因素之间的变化关系，确定函数的自变量、因变量和取值范围(表2)。

2) 根据不同条件下菱形井网储量有效动用变化规律的认识，基于表2中各参数取值，进行计算得到不同条件组合下“均衡驱替系数、无因次有效动用范围”结果——数据分析样本。

利用逐步回归分析方法，可以得到描述“均衡驱替系数σ=f1(λ,JK,p,dS,ε)”、“无因次有效动用范围ω=f2(λ,JK,p,dS,ε)”的非线性变化数学模型。

3)确定菱形井网优化设计目标，如需要同时满足：①均衡驱替系数最大(σmax)；②无因次有效动用范围大于或等于目标值ωmin(如目标值为80%)。则相应的菱形井网优化目标函数为：

(26)

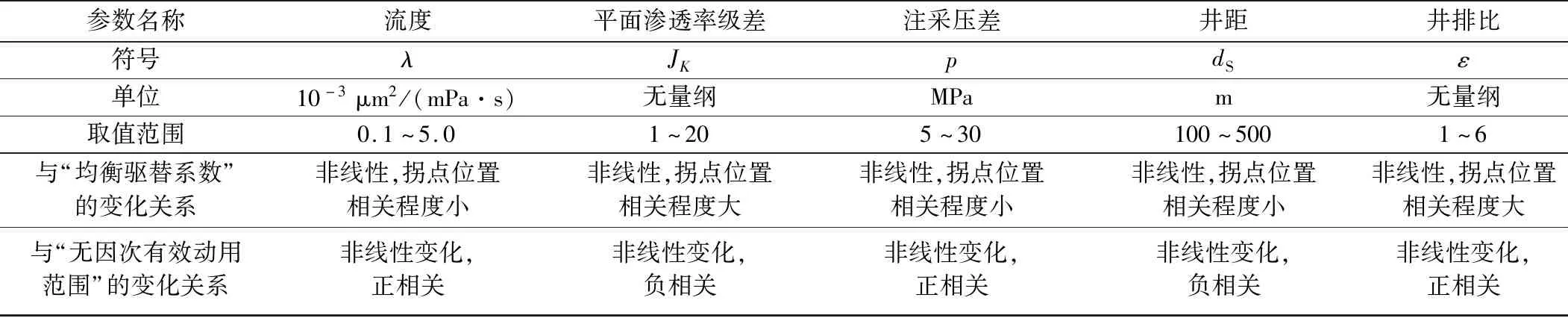
表2 储量有效动用主要影响因素及其取值范围Table 2 Main factors influencing effective development of reserves and their value ranges

4) 根据目标实际油藏条件，确定基础参数的取值，包括：流度、渗透率级差、注采压差和启动压力梯度(与流度相关)等。

利用优化算法(逐步寻优法)，联立求解目标函数，可得到同时满足“均衡驱替系数最大、有效动用范围大于目标值”的菱形井网优化设计参数：合理井距dSm和最佳井排比εm。

根据计算结果，综合考虑实际油田的储量大小、产量要求和经济因素等方面，最终确定菱形井网的优化部署方案。

3.2 基于多元逐步回归建立多因素非线性预测模型

3.2.1 数据样本的多元逐步回归

基于表2中各参数取值，计算得到不同条件组合下的数据样本，然后采用多元逐步回归法，建立多因素非线性模型，主要步骤如下。

1) 保留影响作用程度大的变量，反之则剔除。已知l个自变量和因变量，根据相关系数矩阵R，可求出每个自变量的贡献大小，即：

(27)

式中：Pi为方差贡献系数，无量纲；其中Riy表示第i个自变量对因变量的贡献大小，无量纲；Rii为因变量自相关系数，无量纲。

则第k步计算得出的方差贡献系数为：

(28)

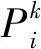
2) 对贡献最小的自变量进行剔除。设定一个显著水平，根据F检验找到其变量剔除临界值Fα。在第k步计算中，假如第j个自变量贡献最大，记

(29)

式中：Pjmax为最大的方差贡献系数，无量纲；h为还没引入模型的自变量，无量纲；Ph为还没引入模型自变量的方差贡献系数，无量纲。计算变量引入的F值判断公式：

(30)

式中：Fopt为所要引入变量的检验值，无量纲；s为数据样品数，无量纲。如果Fopt>Fα，则该自变量引入。若第n步计算中：

(31)

式中：Pjmin为最小的方差贡献系数，无量纲。则根据剔除的F值判断公式：

(32)

式中：Fout为剔除变量的检验值，无量纲。如果Fout≤Fα，则该自变量剔除。

3) 在整个回归计算过程中，自变量的引入和剔除同时进行。经过往复计算，直至不能引入和剔除自变量为止。

3.2.2 多因素非线性预测模型的建立

根据以上不同条件组合下计算的结果，经多元逐步回归分析，得到多因素影响下“均衡驱替系数”变化的计算模型：

(33)

根据以上不同条件组合下计算的结果，经多元逐步回归分析，得到多因素影响下“无因次有效动用范围”变化的计算模型：

(34)

对预测模型进行“回归诊断”检验，通过预测计算结果和分析样本的“残差概率分布”分析，该模型的残差具有明显的正态性，基本服从正态分布，可以认定建立的预测模型可靠。

4 实际油田应用

一般井网设计的方法，首先是利用油藏工程方法，计算油藏合理经济技术井网密度、注采井距界限；然后，设计多套可行方案，利用数值模拟进行计算，再通过指标筛选出最佳方案。而本文方法，考虑了多因素组合条件下的储量动用、均衡驱替效果，实现合理井距和最佳井排比的联立优化求解，可以更精细、更全面地指导基于实际模型的数值模拟研究工作。

4.1 油田基本情况

CY油田为特低渗透各向异性油藏，基本参数如下：油藏中部深度1 190 m，平均有效厚度为26 m；主渗流方向近似为北偏西40°，渗透率为22.3×10-3μm2，垂直主渗流方向渗透率为4.2×10-3μm2；地下原油粘度为4.0 mPa·s；原始地层压力为14.0 MPa，破裂压力约为21.8 MPa，饱和压力5.6 MPa，最大注采压差约为15.0 MPa。通过室内实验和矿场试油、试采资料分析，油藏具有一定启动压力梯度(约为0.012 MPa/m)，整体表现为孔隙渗流的特征，但储层各向异性的影响明显。

根据油田开发实践经验，低渗透油藏在部署初期的菱形反九点井网后，在适当条件下，需要将井网调整为矩形反五点法井网。因此，本文基于实际油藏条件，首先对初期菱形反九点井网进行优化设计，然后分析后期调整为矩形反五点法井网后，对提高储量动用效果的改善程度。

4.2 油田合理井网优化设计及部署

4.2.1 初期菱形反九点井网设计结果

首先，根据油田储层条件和本区相关经济参数，计算油田经济极限井网密度、单井经济日产量界限；其次在满足油田开发经济界限的基础上，确定本区开发井网部署须达到的技术目标(如井网控制区内储量无因次有效动用范围大于80%，采油速度满足开发需要等)；然后，根据本文方法进行“菱形注采井网关键参数寻优计算”，可同时得到CY油田菱形反九点注采井网不同条件下均衡驱替系数、无因次有效动用范围的变化曲线(图6)。

可以看出，在均衡驱替系数变化曲线中，曲线极大值对应的井排比(即满足均衡驱替效果最佳)在2.42左右；而在无因次有效动用范围变化曲线中，当目标值ωmin为80%时，对应的注采井网合理井距为343 m。

4.2.2 后期调整为矩形五点法井网的效果

在低渗透各向异性油藏开发后期，为使井网单元的储量未动用区得以动用，通常将反九点菱形井网加密调整为矩形反五点井网(图7)。

可以用“无因次有效动用范围”、“均衡驱替系数”的增加幅度，来定量描述井网调整后，注采单元中驱替效果的改善程度。对比初期菱形反九点注采井网，后期矩形反五点井网储量动用效果的变化(图8)。

可以看出，初期的菱形反九点注采井网，在调整为矩形反五点井网后，无因次有效动用范围和均衡驱替系数都得到较大提高；井网调整后，无因次有效动用范围和均衡驱替系数的增幅与注采压差均呈负相关关系，说明在注采压差较低条件下，井网调整对注采单元中储量动用程度及储量均衡动用效果的改善作用更显著。

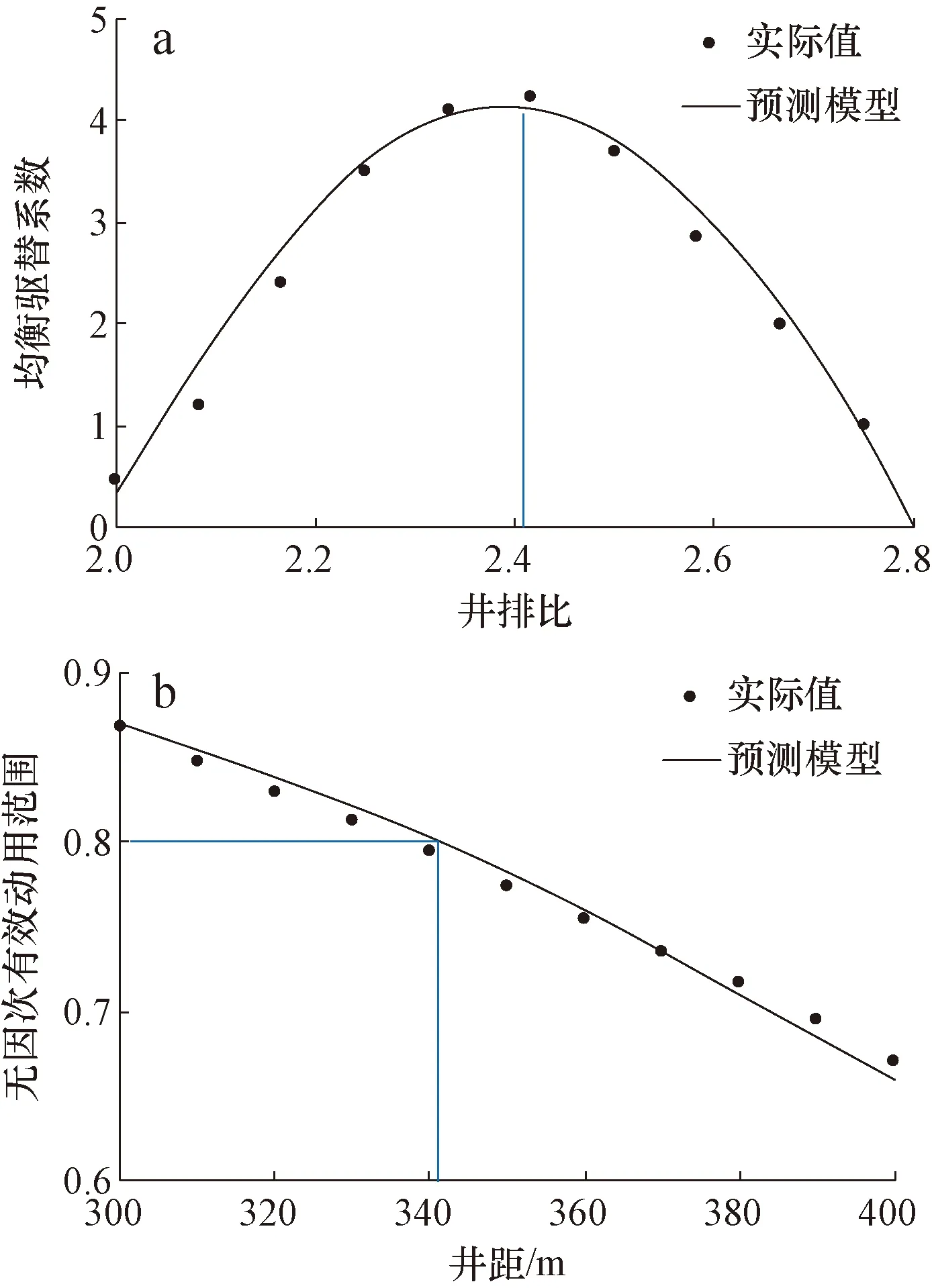
图6 CY油田均衡驱替系数(a)和无因次有效动用范围(b)变化曲线Fig.6 Curves of equilibrium displacement coefficients vs. dimensionless effective development range variation in CY oilfield

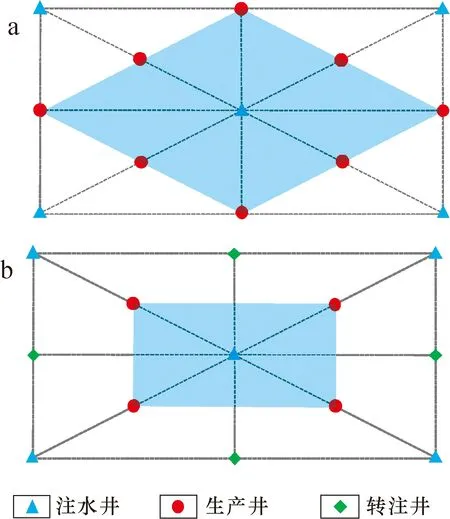
图7 井网调整方式Fig.7 Well pattern adjustment modea. 初始菱形反九点井网 b. 矩形反五点井网

4.2.3 油田合理井网部署建议

基于以上井网论证的结果，来指导油藏数值模拟中计算方案设计，以实现油田优化注采井网的目标，既能实现均衡驱替、又满足储量有效动用程度，为高效开发该类油田奠定基础。CY低渗透各向异性油藏采取菱形反九点井网形式，在平行主渗流方向拉长井距(约340 m)，在垂直主渗流方向缩小排距(约140 m),油田井网设计部署结果见图9。

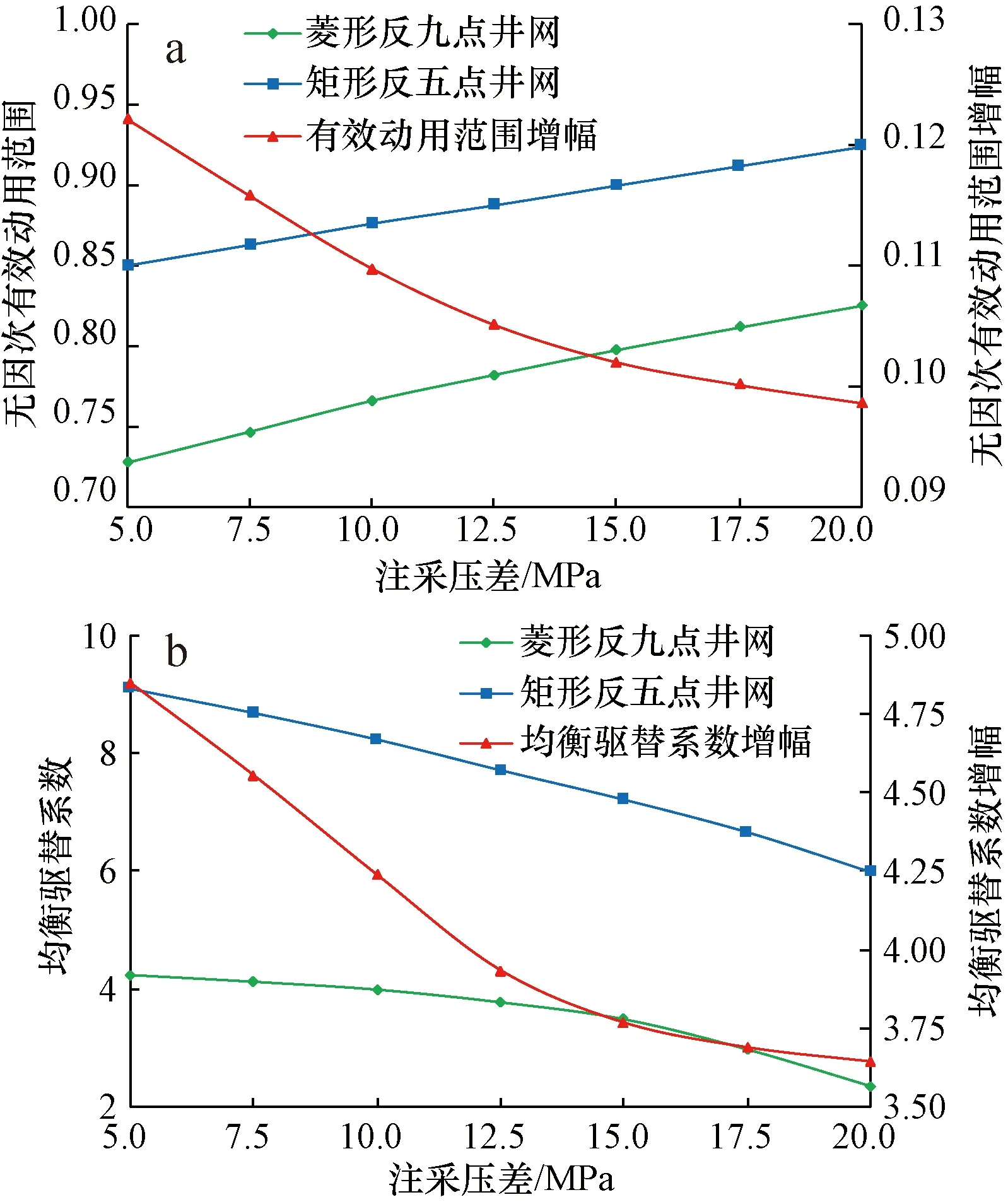
图8 井网调整后储量动用效果改善程度变化曲线Fig.8 Curves showing displacement equalization effect and improvement of reserve producing after well pattern adjustmenta. 无因次有效动用范围 b. 均衡驱替系数

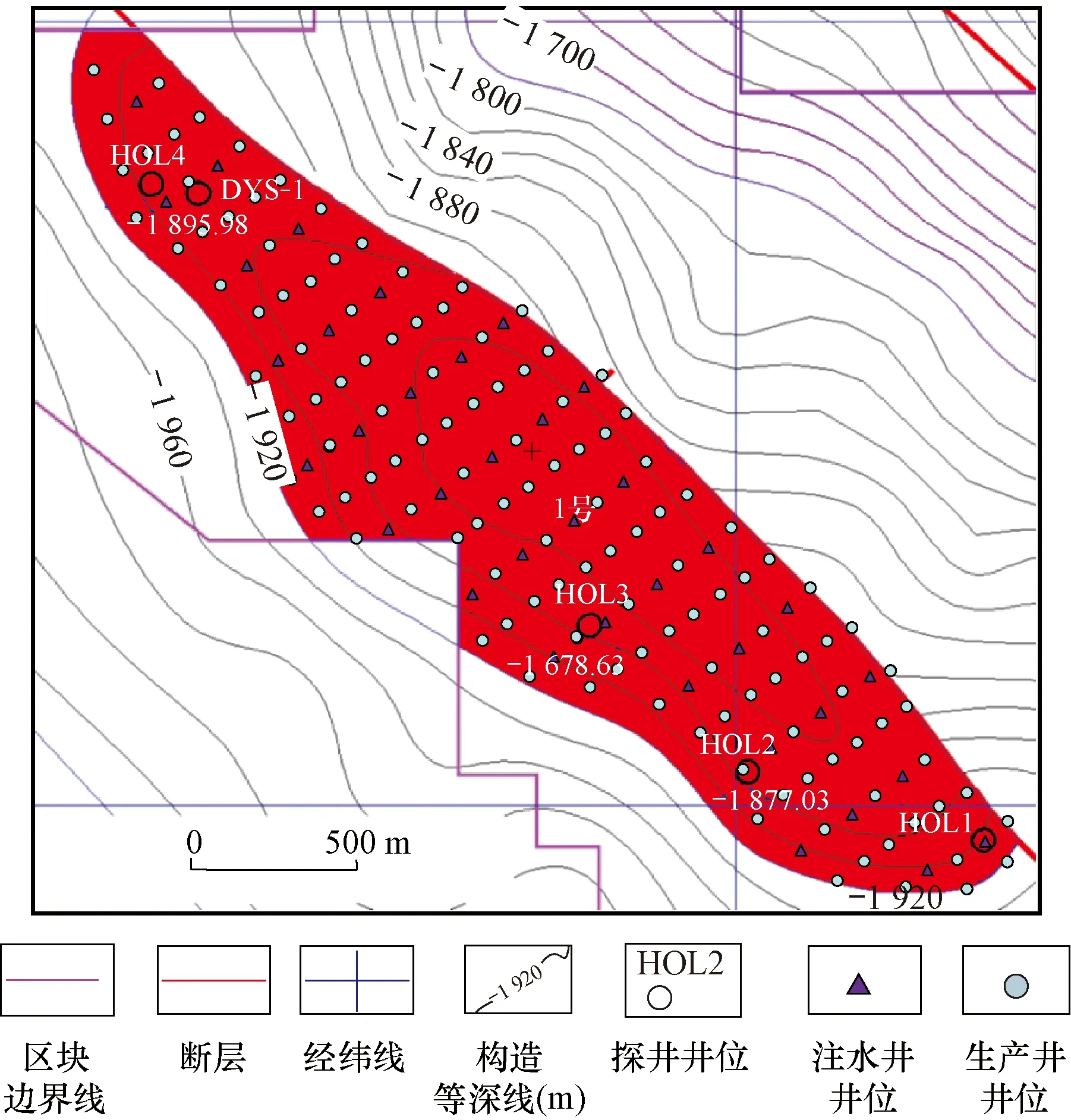
图9 CY油田菱形反九点注采井网设计部署Fig.9 Diagram showing design of rhomboid reverted nine-point well pattern in CY oilfield

5 结论

1) 考虑启动压力梯度和各向异性的影响，建立了菱形井网形式下的渗流方程，推导出菱形井网注采单元渗流场分布解析解，可得到不同条件下注采单元中压力、速度分布的变化规律。

2) 利用注采单元中的速度分布变化来表征和反映储量动用状况，进而建立评价低渗透各向异性油藏有效开发的方法，得到不同条件下储量有效动用范围、注采均衡驱替效果的变化规律。

3) 建立同时满足“储量有效动用程度满足油田开发要求、注采均衡驱替效果好”的菱形注采井网优化模型，形成菱形井网优化设计方法。实例应用表明，该方法可用于确定菱形注采井网合理井距、最佳井排比，具有很好的实用性和可操作性。