基于遗传算法的应急物流设施选址与调度

冯瑛杰， 谢庆红

(南京工业大学 经济与管理学院， 南京 211816)

对资源的不断索取以及人口密集化等因素使得各种灾害风险不断交织，不断叠加，各种自然灾害、社会事故屡见不鲜，对人们正常生活造成严重影响，威胁着其生命安全，人们所面临的形势和困难前所未有。各类突发性事件考验国家灾害处置能力。提前建立好应急物流设施，合理地选址以及布局不仅能及时应对突发事件，保障救援工作快速运行，更能进一步丰富完善中国应急体系建设。

目前，国内外许多学者对应急物流设施选址问题中的不确定性因素进行了研究。冯春等[1]计算比较了鲁棒优化模型RO和随机优化模型SO两类选址模型，证明鲁棒优化法相对于随机优化法的优异性。杜博等[2]以各项成本为目标建立了两阶段鲁棒优化模型，协同优化预选址、重选址之间关系并与传统p中心模型比较。高雷阜等[3]在构建确定型模型的基础上将不确定因素描述为椭圆形集合，建立目标函数为最小加权距离鲁棒优化模型。Karamyar等[4]研究了不确定情景下医院的选址和服务分配鲁棒模型，并用包含模拟退火法以及Benders分解的混合算法对模型进行验证。De Mattos[5]以成本为主要因素建立鲁棒模型，并用分层优化的方法减轻每个约束所设置特定鲁棒性的负担。张聆晔等[6]考虑海上应急效率，通过离散情景对鲁棒优化模型求解。郭子雪[7]等学者利用梯形模糊数为参数，以加权距离最小为目标函数构建选址模型并进行了验证计算。朱晓霞等[8]分析选址影响因素建立了混合多属性指标体系，并将这些指标转化为三角模糊数对模型进行计算。Yadav等[9]将模糊逻辑与分析网络过程相结合，呈现旋风灾害防备活动的识别与评估过程。Sarma等[10]用梯形模糊数和中智数表示模型中的不确定参数，以应对灾后应急设施选址成本最小化问题。赵远飞等[11]通过分析应急设施选址各种因素，利用层次分析法对TOPSIS法改进，科学有效地处理选址优化问题，提高了模型的适应性。

上述文献大多以鲁棒优化以及模糊数等方法解决模型中的不确定性参数，本文以前者理论研究为基础，针对突发情景下数据短缺、需求不确定等问题，采用基于灰色预测模型对需求进行预测并通过非支配排序遗传算法对模型进行求解，并通过实例对模型有效性进行相关验证。

1 应急物流设施选址模型构建与求解

1.1 问题描述

为预防突发事件需要在若干个地点选择建立应急物流设施，在有限时间内预测应急物资数量并运送至已知需求点，实现快速对受灾地区进行救援。假设已知受灾区域物资需求点，应急物流设施只能从若干备选点选择，且各应急物流设施均能满足需求点供需要求；各受灾区域需求点对救援物资的需求量是不确定的，可由多个应急设施提供物资输送并且应急设施可向多个需求点提供服务。

选址模型需要解决的问题是: 对各个需求点所需要的物资进行预测；在满足目标函数下求得最优Pareto解集并得到选址以及调度方案。

1.2 基于联系数的区间灰数

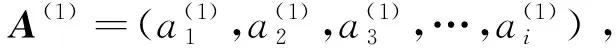
1.3 参数定义

I为已知需求点集合，i∈I；J为潜在应急物流设施备选点集合，j∈J；Qj为应急物流设施最大储备容量；qj为应急物流设施现储备物资量；cj为建立应急物流设施所需相关成本；⊗i为需求点i预测物资需求量；lj为应急物流设施物资储存成本；pij表示由备选点j运送物资到需求点i的单位价格；tij表示由备选点j运送应急物资到需求点i所需要的时间；μi为未能满足需求点i物资所产生的惩罚成本；wi为各个需求点的权重；θi为未能在响应时间内完成需求点i服务的延时成本；Ti为各个需求点物资服务需要的响应时间。

决策变量：qij表示由备选点j运送物资到需求点i的数量；Xj为0～1变量，当Xj取1时，表示在该点建立应急物流设施，取0则表示不建立；γij为0～1变量，当γij取1时，表示备选点j向需求点i运送应急物资，否则不运送。

1.4 模型建立

建立的多目标优化模型是选取若干个应急物流设施，使得受灾区域所建立设施到需求点满足时效性、满意度、成本3个目标。依据上述建立如下优化模型：

1)目标函数。为满足时效性目标，建立子目标F1为

(1)

式(1)表示最小化备选点j运送物资到需求点i的总时间。

为满足服务满意度目标，建立子目标F2为

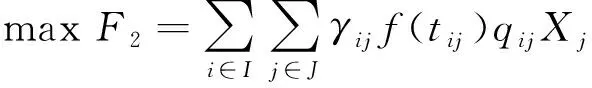
(2)

式(2)是为了所覆盖区域需求点满意度最大化，为了简便计算，引入文献[14]中线性时间满意度函数，同时设立参数Li和Ui，前者表示为需求点i非常满意时所能接受的最长等待时间，后者表示为需求点i非常不满意时的最短等待时间，当tijUi时，f(tij)=0；当tij∈[Li,Ui]时，f(tij)=(Ui-tij)/(Ui-Li)。

为满足成本目标，建立子目标F3为

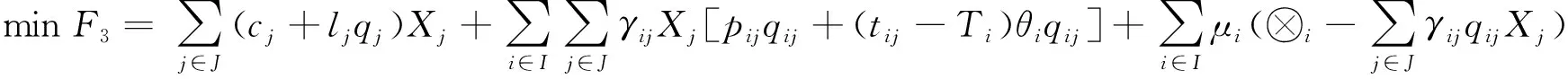
(3)

式(3)表示整个应急物流系统所产生的费用最低，第1项表示设施建设成本和运营成本，第2项表示应急物资运输成本以及未达到响应时间产生的延时成本，第3项表示未满足需求点服务产生的惩罚成本。

2)约束条件。各应急物流设施点容量存在限制，即

0≤qj≤QjXj

(4)

建立的应急设施数量应该满足

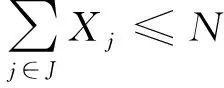
(5)

只有备选点已建立应急物流设施才能向需求点运送物资,即

∀i∈I,γij-Xj≤0

(6)

任一需求点至少有一个应急物流设施进行物资运送，即

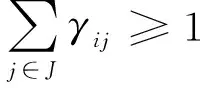
(7)

需求点物资最低需求必须得到满足

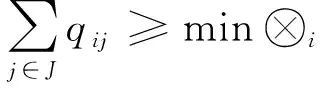
(8)

运送物资的数量不超过备选点现有容量，即

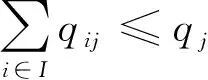
(9)

γij∈{0,1},Xj∈{0,1}

(10)

1.5 模型求解

建立的选址模型可归纳为多目标优化问题(MOP)，它包含3个目标函数：时间、成本、满意度，3个目标函数之间存在一定制约关系，无法同时得到三者的最优解。因此采用带精英制的非支配遗传算法(NSGA-Ⅱ)[15]对模型进行求解。该算法基本流程如下：

1)种群初始化。采用实数编码的形式随机产生Pt个个体组成种群，假设突发事件种类为1，需求点为i，待选应急物流设施点为j，则该模型决策变量为(2i+1)j个。

2)快速非支配排序。选取两个个体分别记为xi与xj(j≠i)，比较它们的支配关系，相比之下xi最优则将它进行标记。令i=i+1，所找到的每个最优的个体被称为非支配个体。这些最优个体组成第一级非支配层，然后，去除已被标记的非支配个体，再重复上述步骤，得到第n级非支配层。

3)拥挤度计算。在每一个非支配层对个体依据目标函数值进行排序，计算个体的拥挤度。

4)遗传操作。和传统遗传算法一样包含选择、交叉、变异3部分。首先通过锦标赛的形式从父代种群选取两个个体，对选择的个体进行交叉，交叉点随机生成直至产生规模大小和父代种群一样的子代种群，选择部分个体变异。

5)精英策略。将子代种群放入父代种群形成2倍大小的新种群，以非支配排序后以及拥挤度计算选取优良个体构成下次迭代的父代种群，重复前面步骤直到程序结束。

NSGA-Ⅱ算法流程如图1所示。

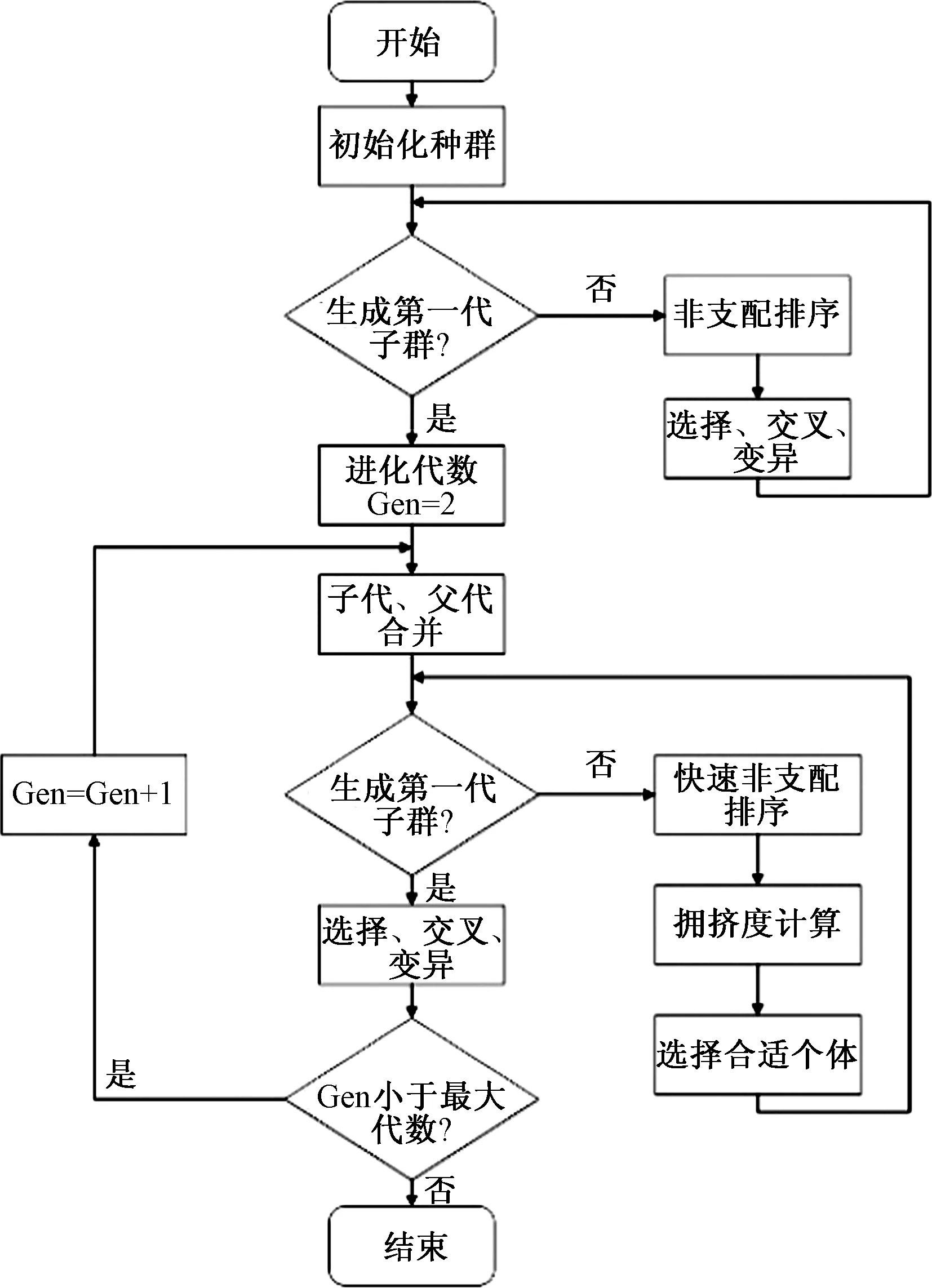
图1 NSGA-Ⅱ算法流程

2 实例分析

某地区应急物资需求点的数量为8个，需要在10个应急物流设施备选点选取若干个对需求点进行物资输送。已知应急物资单位储存成本为1万元/万件，应急物资的运输成本为0.2万元/万件，未能在响应时间内送达的延时成本为1.2万元，运送应急物资未能满足需求点需要的惩罚成本为5万元。表1为应急物流设施备选点相关参数设置，表2为各备选点到达需求点的时间。

表1 拟建应急物流设施建设成本和储备容量

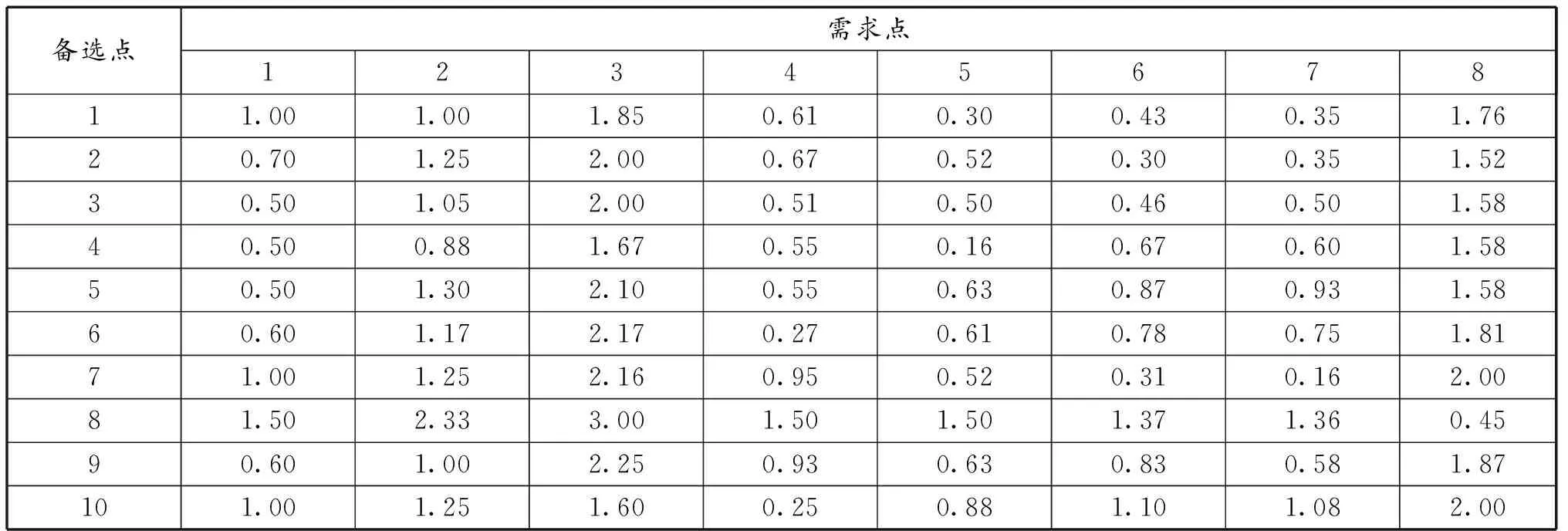
表2 拟建应急物流设施备选点到需求点的时间 单位：h

2.1 需求预测

对8个需求点应急物资需求量进行灰色预测，预测结果见表3。预测模型检验结果见表4。通过计算级比表示该数据可以用灰数模型进行预测，从平均级比偏差值和残差可以看出两者均小于0.1，相对误差较小，表示达到较高要求。其中同部序列方差比为0.126，异部序列方差比为0.468 1，建模精度分别为1级、2级，表明对应急物资的需求预测具有较高的精度，预测结果较为准确。

表3 各需求点的预测需求量、响应时间以及需求点的权重wi

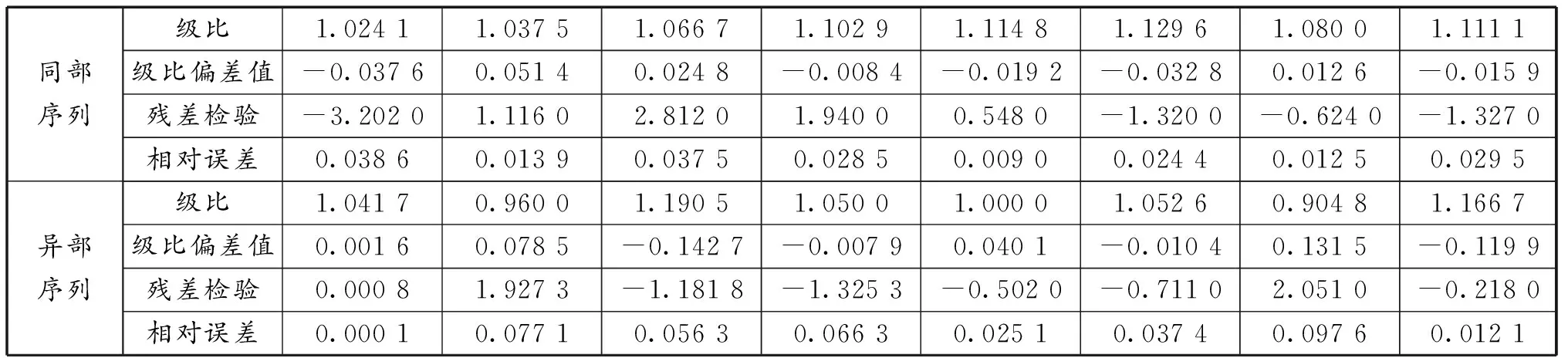
表4 预测模型检验结果

2.2 模型求解

实验过程通过Python编程，初始种群规模大小设置为500个，交叉概率设为0.9，变异概率为0.1，进行1 000次迭代，算法不断迭代直至收敛总用时19.9 s，共找到非支配个体数500个，单位时间找到帕累托前沿点个数为25个，帕累托最优解集分布如图2所示。模型所得选址结果为(0,1,0,1,1,1,0,0,1,1)，即在备选点2、4、5、6、9、10建立应急物流设施，表5为模型运行结果中的4个物资调度方案目标函数值，表6为方案1的具体调度措施。

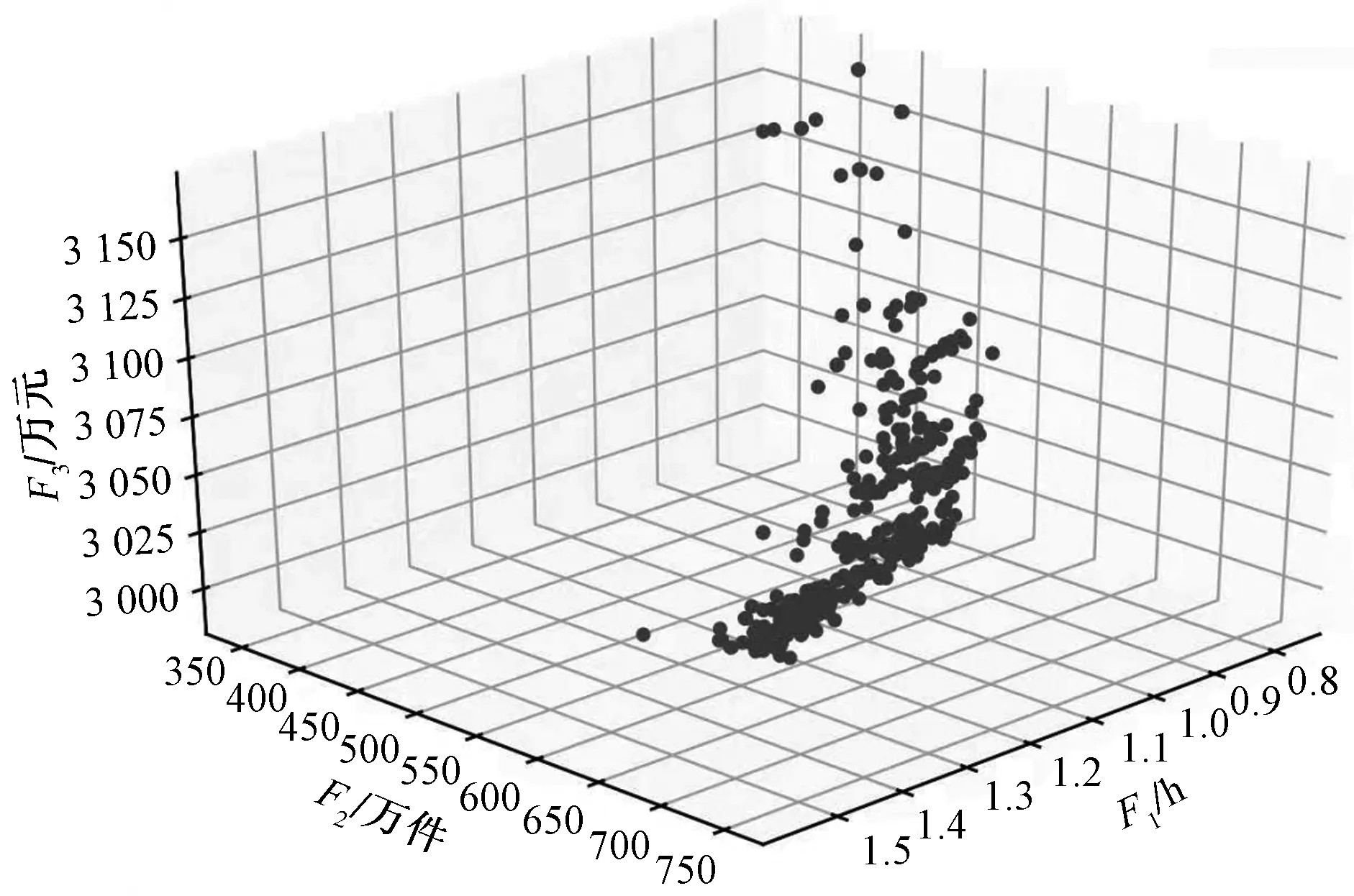
图2 帕累托最优解集分布

通过对表5进行分析可以看出，运送时间、服务满意度、总成本3个目标函数之间紧密联系又彼此限制，当运送时间一定时，服务满意度的增加会导致总成本的增加；当服务满意度一定时，增加总成本可以减少救援时间；当总成本恒定，运送时间的减少导致救援物资数量较少，降低了服务满意度。对于决策者而言，如果要尽可能地提高需求点服务满意度，那么可以通过增加应急物资的数量、提高救援速度等方式；如果要在最低满意度的情况下，尽可能地减少救援时间，则需要对成本进行投入。

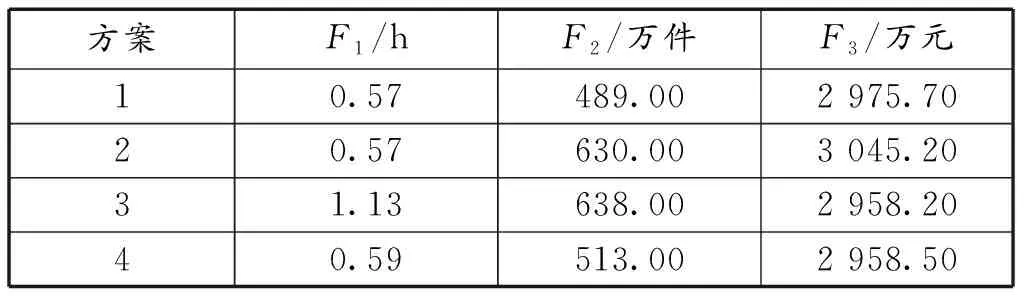
表5 调度方案目标函数值

由表6可知，当指标为1时，选建应急物流设施才能对需求点进行服务，如需求点7和8由2号备选点服务。观察表格可以发现应急物资运送数量均能满足需求点的最低需求，且调运的数量小于设施持有量，4、5备选点所建设施仓库容量远大于物资调运量，决策者可适当减小物流设施规模以免造成资金浪费。由于突发事件下所处情景不同，决策者决策偏好侧重点也不一样，本文所得选址以及调度方案具备一定参考价值。

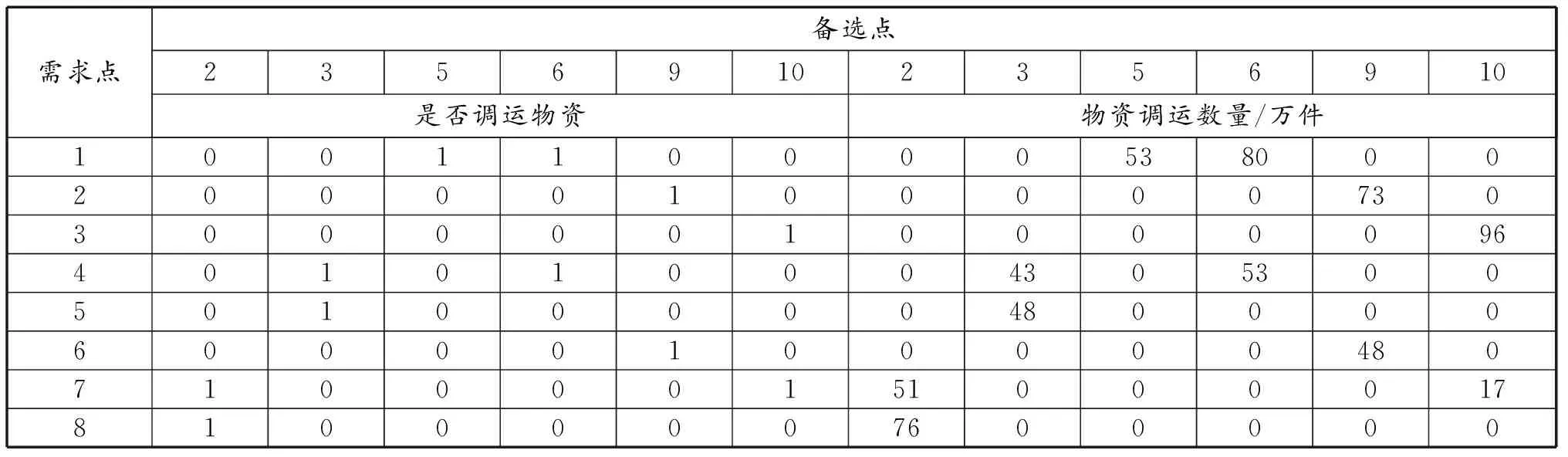
表6 方案1具体调度措施

3 结论

建立了以总成本、运送时间、服务满意度为目标的应急物流设施选址模型，通过灰色预测模型对需求点进行应急物资预测将突发事件下的需求不确定性进行转化，同时利用NSGA-Ⅱ对选址多目标优化问题进行求解，所得Pareto前沿分布均匀，算法稳定性好，对实际选址问题具有一定参考性。

研究仅对需求的不确定性进行了重点分析，忽视了突发事件以及需求物资的多样性等不确定因素，今后研究可将多种不确定性因素纳入模型中。