矿井涌水量渗透系数构造分形优化研究

徐 慧，牟 义，牛 超

(1.煤炭科学技术研究院有限公司 安全分院，北京 100013；2.煤炭资源高效开采与洁净利用国家重点实验室 ，北京 100013；3. 西安科技大学 地质与环境学院，陕西 西安 710054)

0 引 言

渗透系数是水文地质中最常用的评价参数，不仅是含水层富水程度评价重要指标，更是矿井涌水量预计、信息融合突水预测、岩体稳定性评价等定量计算的重要指标。在矿井水防治过程中，构造应力场的影响无处不在，导致断层、褶曲等构造具有分区和不均一性，而断层、褶曲的不同发育程度决定着岩层渗透率的变化，影响到矿井涌水量预测精度。因此，能否用数学语言准确定量地描述地质条件的复杂程度对了解特定区域(采区、巷道、工作面等)内的岩体渗透性至关重要。

目前，不同领域的学者、专家针对渗透系数优化方面做了大量的研究。张道勇[1]发现了从传统意义上的抽水试验或室内模拟试验获得的渗透系数值作为参数计算会带来较大误差，渗透系数尺度效应带来的这种误差具有普遍性，如何利用分形理论找到实际含水层渗透系数是重要的研究方向。肖红宇等[2]将土体孔隙比表面积分形模型引入土体渗透性的研究。褚卫江等[3]在固结算例中优化了分形渗透系数模型，将模型通过数值计算，显示具有良好的规律性。齐钒宇等[4]将分形理论应用到矿床和元素的预测评价中，寻求分布和富集规律。张彦洪等[5]通过采用信息维数来寻找裂隙密度与渗流的相关性。韩启迪等[6]利用DLA模型对不同情况下成矿流体的渗透过程进行模拟,在一定程度上揭示了成矿流体渗透过程的分形生长机制。杨阳等[7]将分形理论应用到单轴压缩下饱水粉砂岩破裂过程中，寻找红外辐射规律。何若象等[8]运用数值方法预测混凝土水的渗透系数。段祥宝等[9]用分维数判断土体的渗透变形形式。贺拿等[10]运用试验手段寻找渗透系数K与分维值D之间的关系，发现有明显相关性，为泥石流启动的临界雨量预测研究提出新的思路。尹尚先等[11]将分形理论运用到“大井法”矿井涌水量预测中，优化了渗透系数取值，与实际更加符合。胡建军等[12]引入分形理论研究金属矿山采空区形状特征,为复杂采空区形状特征研究提供了一种新的方法。

笔者在总结国内外专家学者研究成果基础上，将分形理论运用到赵庄二号井内的构造复杂程度定量化评价及构造分形与渗透系数指标关系研究方面。首先以分维数中的容量维为基本特征量，通过选用网格覆盖法定量评价赵庄二号井矿井构造的复杂性，利用分形维数能很好地反映出地质构造复杂程度这一特点，在网格中将断层、褶皱等构造的走向、尺寸及范围等构造指标的情况标记出来，并给予断层和褶皱不同权重的分形维数，较传统数学统计方法，能更精细地进行构造复杂程度定量化评价；将研究成果应用到赵庄二号井，对该矿井的构造复杂程度进行定量分析评价，采用相关系数法分析了构造分形指标与渗透系数指标的关系，优化修正了渗透系数，将优化后的渗透系数用于矿井涌水量的预测，提高涌水量预测的准确性。

1 矿井地质概况

1.1 地质概况

赵庄二号井位于山西沁水煤田东南部，地层由老至新为：震旦系、寒武系、奥陶系、石炭系、二叠系、古近系、新近系及第四系。赵庄二号井内地表大部分区域被第四系黄土所覆盖，仅西部出露二叠系上统上石盒子组上段(P2s3)地层，零星出露二叠系上统上石盒子组中段(P2s2)地层。赵庄二号井主要可采煤层山西组3号煤层和太原组15号煤层。

1.2 水文地质概况

沁水盆地东南部处于黄河水系丹河流域和海河水系浊漳河流域的交界处，水文地质系统隶属于延河泉岩溶水、三姑泉岩溶水和辛安泉岩溶水3大系统。赵庄二号井内主要含水层从上到下有：第四系松散层孔隙含水层组、新近系基岩风化带裂隙含水层、二叠系K8砂岩裂隙含水层、二叠系砂岩裂隙含水层、石炭系岩溶裂隙含水层、奥陶系石灰岩岩溶裂隙含水层。二叠系各砂岩含水层之间和太原组各薄层灰岩含水层之间都存在厚度不等的由泥岩、砂质泥岩、粉砂岩组成的隔水层。在没有构造沟通情况下，这些隔水层可有效地阻隔各含水层之间的水力联系。

1.3 构造概况

赵庄二号井位于晋(城)-获(鹿)褶断带南段的韩店至高平间褶断带西侧，武(乡)-阳(城)凹褶带东侧。新华夏构造体系主要控制区内构造，北北东走向，为倾角5°左右，倾向北西的单斜构造，并伴有次级宽缓褶曲和小型断裂。

赵庄二号井共发现大小褶曲9条，多数集中在赵庄二号井的东北部和中部区域。赵庄二号井内落差大于30 m的断层有2条，为兴旺庄南正断层和庄头正断层，兴旺庄南正断层由西南至东北穿过整个赵庄二号井，走向NE，倾向SE，倾角70°～80°，赵庄二号井内最大落差30 m，控制长度1 310 m；庄头正断层位于赵庄二号井的南边界，全长26 km，倾向北北西，倾角75°，落差290 m；通过三维地震勘探探明赵庄二号井内落差在3～18 m的断层20个，陷落柱9个。

2 矿井构造定量化评价

以赵庄二号井为例，具体介绍运用分形理论对矿区构造复杂程度进行评价的方法。

2.1 分形计算

分形(Fractal)，属拉丁语Frangere，由芒德布罗(B.B.Mandelbrot)在1973年创造[13]。Fractal表示不规则形状，而分形几何学就是研究不规则几何形态的几何学。分形维数是分形几何学中的重要参量，用来描述分形的基本特点，常用的分形维数有相似维数、豪斯道夫维数、容量维数、计盒维数等。这里研究采用容量维数对赵庄二号井构造复杂程度进行评价。

以赵庄二号井收集到采矿、地质资料为基础，使用容量维数中的网格覆盖法对赵庄二号井构造进行统计，分别计算各单元各分区的分维值(容量维数)。断层网格的容量维数计算方法[14]如下：分别用面积为1 000 m×1 000 m、500 m×500 m、250 m×250 m、125 m×125 m的方形网格叠加到地质构造图上，形成密集度呈指数级增加的方形格网，分别统计含有断层迹线的网格的个数，具体方法如图1和图2所示。

图1 赵庄二号井构造分形评价单元分区Fig.1 Study area structure fractal evaluation unit partition

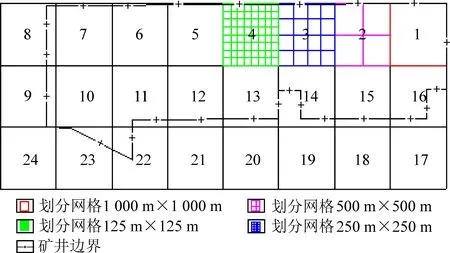
图2 断层网格分区划分Fig.2 Fault grid partition

2.2 构造定量评价

在矿井构造中，断层与褶皱对含水层富水性影响不同，查阅大量相关资料与文献，结合矿上实际情况，对断层和褶皱分别赋予不同的权重，断层为0.6，褶皱为0.4，得出构造分形维数的修正公式：D=0.6a+0.4b，其中a、b分别表示断层与褶皱的分形维数。

通过分区计算出赵庄二号井单元构造区的断层容量维和褶皱容量维数据，然后根据修正公式中断层和褶皱不同权重值得出整个赵庄二号井的构造分维数，见表1。分维维数分别表示所在分区单元中心点数值，从而可以看出不同细化的分区单元对赵庄二号井内的构造网格复杂程度进行不同程度的量化。

表1 赵庄二号井构造分形维数计算结果Table 1 Calculation results of structure fractal dimension in Zhaozhuang No.2 Mine

结合赵庄二号井全区和分区双对数线性回归分析结果，赵庄二号井容量维值为1.166 5(图3)，相关系数大于0.99，表明赵庄二号井构造网格均匀分布在全区，单元数据相关性较好。把分区中心点的坐标值和容量维值录入计算程序中，编制出赵庄二号井断层网格容量维叠加图(图4)。

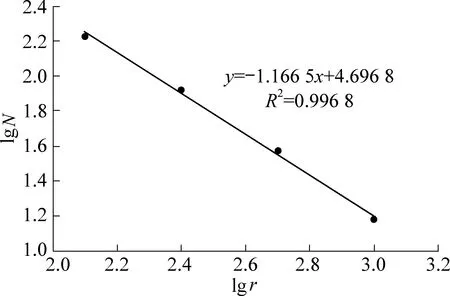
图3 全区分单元双对数拟合Fig.3 Full logarithm fitting

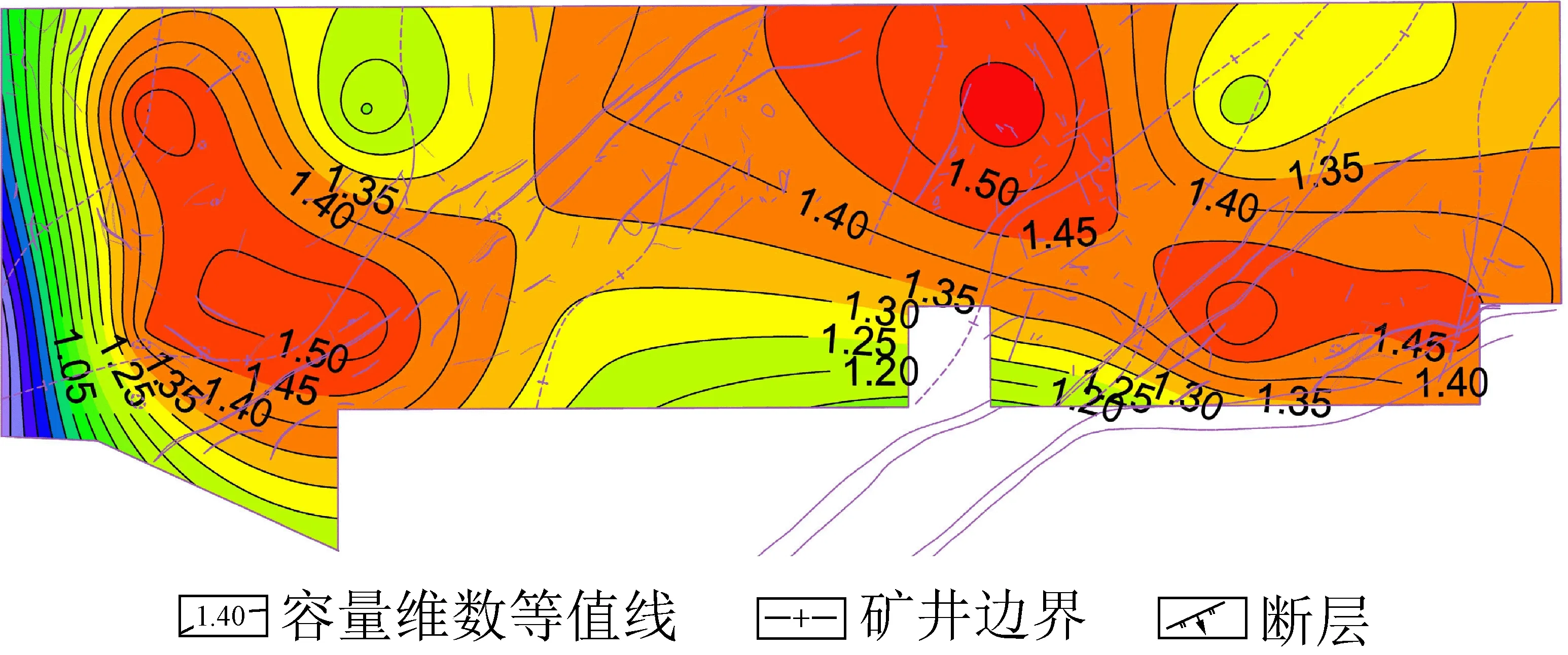
图4 赵庄二号井构造网络容量维叠加Fig.4 Research area construction network capacity dimension plan

从图4可以清楚地看到红色区域基本集中在赵庄二号井的东北和西南部条带，构造分形维数均在1.4以上。在东北条带上遍布着褶皱，如布村向斜、布村背斜、应城向斜、应城背斜、南张向斜、南张背斜等，还分布着5条落差在16 m以上的断层：DF3(长度350 m，倾角75°，落差18 m)、DF31(倾角75°，落差40 m)、DF54(倾角73°，落差16 m)、DF32(倾角70°，落差36 m)和DF55(倾角78°，落差36 m)，更有庄头正断层自南边界穿过。在赵庄二号井西南部条带除了发育着郭家庄向斜、郭家庄背斜和DF40(倾角70°，落差24 m)这种大的构造还伴随着数十条次生构造。以上数据表明赵庄二号井的东北条带和西南部断裂发育。

东北区和西南区条带中内构造发育较其他分区丰富，容量维值明显高于其他断层发育较弱的分区，赵庄二号井全区的平均容量维数为1.166 5，说明该赵庄二号井范围内构造相对复杂，但从图4中可看出区内构造复杂程度明显具有不均一性。

3 渗透系数优化

3.1 渗透系数优化

构造发育程度对岩层渗透性能具有控制作用，两者之间是否存在一定联系。为解决这个疑问，笔者找出抽水孔所在位置的分形维数与该孔测出的渗透系数，通过比较，发现构造容量维与渗透系数之间存在相关性，且呈正相关关系，通过曲线拟合形成构造容量维与渗透系数的关系式(图5)，优化修正了渗透系数K。优化公式，得

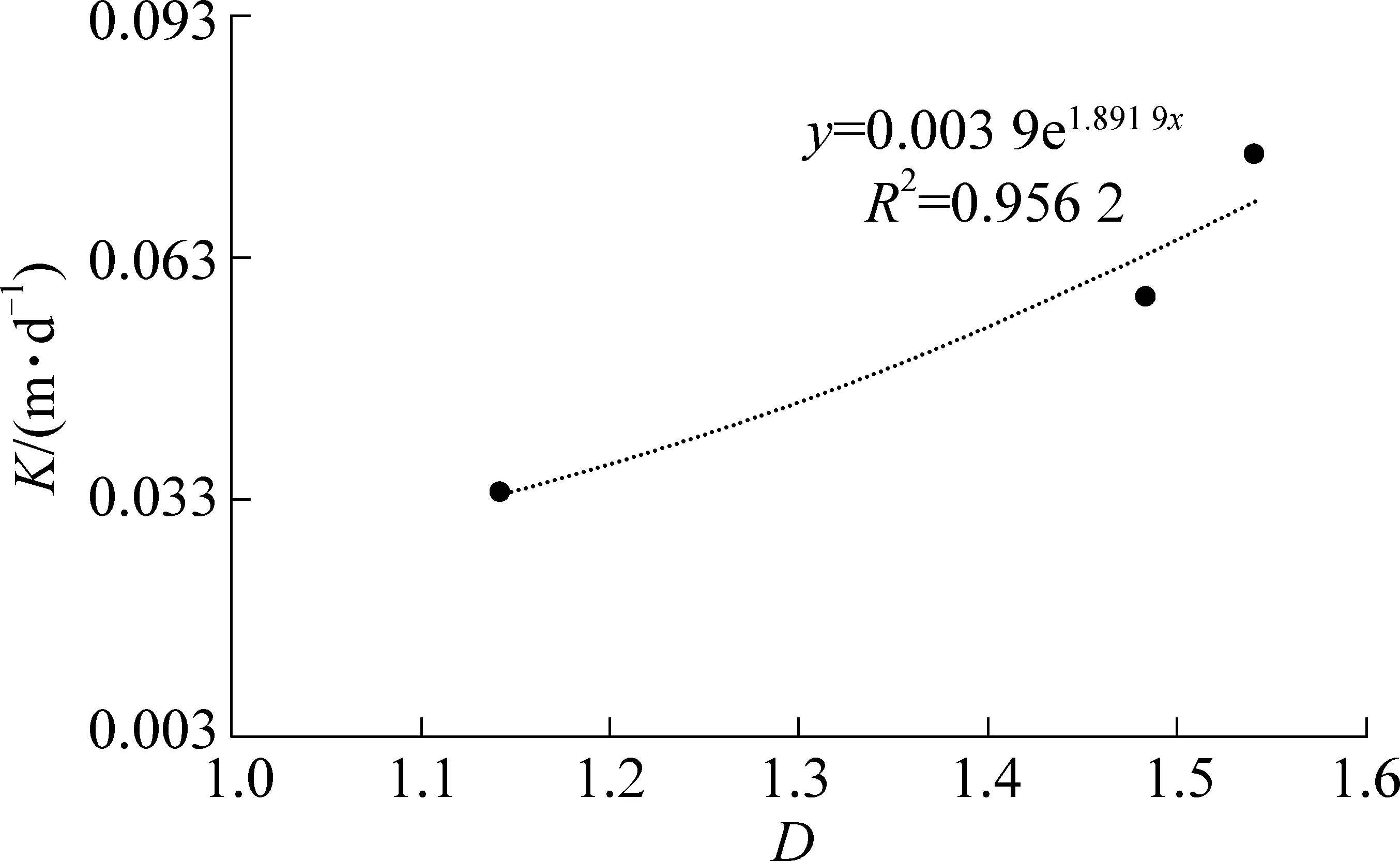
图5 构造容量维与渗透系数拟合曲线Fig.5 Tectonic capacity dimension and permeability coefficient fitting curve K*=0.003 9e1.891 9D

(1)

式中：K*为渗透系数K的优化值。

3.2 涌水量预测

将此优化公式运用到赵庄二号井2309工作面的涌水量预计中去。预测方法采用“大井法”，计算结果见表2。计算公式为

表2 涌水量预测对比Table 2 Water inflow forecast comparison

(2)

式中：H为水柱高度，m；M为含水层厚度，m；R0为影响半径，m；r0为大井的引用半径，m。

4 结 论

1)定量评价了赵庄二号井的构造复杂程度，计算出赵庄二号井全区的容量值为1.166 5，表明赵庄二号井内构造相对复杂，从全区构造网络容量维叠加图中可以看出，区内构造复杂程度具有明显的不均一性。

2)利用相关性分析法发现构造容量维与渗透系数间呈正相关性，从而对渗透系数进行了优化，并获得优化公式。将优化结果运用到赵庄二号井2309工作面“大井法”涌水量预测过程中，相对误差从42.5%降到了7.8%。实践表明，“大井法”采用优化后的渗透系数进行矿井涌水量预测，可以提高准确率。

3)以赵庄二号井为例，将分形理论中的容量维引入煤矿构造复杂程度的评价研究中，实现了矿州构造复杂程度定量的评价及渗透系数优化，对赵庄二号井的矿井防治水及瓦斯防治等方面有重要的意义。

致谢：感谢山西晋煤集团赵庄二号井地测科提供相关资料，同时感谢山西晋煤集团物探工程分公司以及煤炭科学技术研究院有限公司安全分院晋城项目部的大力支持和帮助！