Fano interference and transparency in a waveguide-nanocavity hybrid system with an auxiliary cavity∗

Yu-Xin Shu(树宇鑫) Xiao-San Ma(马小三) Xian-Shan Huang(黄仙山)Mu-Tian Cheng(程木田) and Jun-Bo Han(韩俊波)

1School of Electrical Engineering&Information,Anhui University of Technology,Maanshan 243002,China

2School of Mathematics and Physics,Anhui University of Technology,Maanshan 243002,China

3Wuhan National High Magnetic Field Center and Department of Physics,Huazhong University of Science and Technology,Wuhan 430074,China

Keywords: Fano interference,waveguide quantum electrodynamics,auxiliary cavity

1. Introduction

Realization of strong coupling between atoms and photons plays important roles in quantum information processing. Many groups have reported the realization of strong couplings between atoms and photons in one-dimensional waveguide in recent years.[1–9]Typical waveguides include metallic nanowires,[1]fibers,[2]supercondcuting transmission lines[6,7]and photonic crystal waveguides.[3,4,9]Based on the strong coupling,photon scattering properties in the one-dimensional waveguide have also been investigated widely.[10–38]By controlling single photon reflection and transmission spectra, different kinds of quantum devices and quantum logic gates have been proposed and realized, which includes single photon switching,[10–12]transistors,[13–15]diodes,[16,17]routers,[22–24,27]circulators,[28,29]and frequency-combs.[25,26]An atom-waveguide system with strong coupling is also a good platform to investigative many quantum effects,such as collective emission,[39]collective Lamb shift,[40]and photon bound states,[41]due to the phase (or time delay) induced by photons propagating in waveguides. Many of these developments can be found in the recent excellent reviews.[7,42–45]

It is well-known that photonic crystal (PhC) cavity can enhance the interaction between photons due to its ultrasmall mode volume and low dissipation rate. Thus, there are many reports on single photons transporting in waveguides interacting with a quantum emitter embedded in a PhC cavity. The photon scattering properties can be manipulated by the frequency of the PhC cavity,the interaction strength between the atom and the PhC cavity,etc.

On the other side, several investigations show that many quantum optical phenomena induced by the interaction between atom and photon in a PhC cavity can be manipulated by an auxiliary cavity (AC). Recently, Liuet al.investigated the vacuum Rabi oscillations for a single quantum emitter insider a cavity, where the cavity couples to an AC.[46]After that, Chen predicted that AC can induce vacuum Rabi splitting in a semiconductor quantum dot-first cavity system.[47]Furthermore, the ACs enhancing the dipole induced transparency[48]and manipulating the optomechanically induced transparency[49]have also been reported recently. In most of these models, the AC and the PhC cavity are coupled directly. In this paper, we investigate ACassisted controlling Fano interference effects and transparency in the transmission spectrum of single photon scattering. In our model, the AC and PhC cavity are coupled through the waveguide, thus they interact indirectly. For a more general case, the PhC cavity is denoted as the first cavity (FC). The calculations show that the Fano dips and locations of transparency window depend strongly on the eigen frequency,coupling strength and location of the AC. The scheme may pave the way towards the realization of solid integrable quantum devices at single-photon levels.

2. Theoretical models for AC-assisted controlling single photon transport

The model we consider is shown in Fig. 1. The FC and AC are coupled by a waveguide. The separation between the FC cavity and AC isL.Jc(Ja)denotes the coupling strength between the FC (AC) and the waveguide. An atom with ground state|g〉and excited state|e〉is embedded in the FC.The configuration can be realized in the solid system using a usual photonic crystal technique.[30,50]A parallel line-defect photonic waveguide sustains the photon propagation, which couples to two separated point-defect cavities. A quantum dot is embedded in one of the point-defect cavity.The other pointdefect cavity plays the role of AC.A similar possible physical configuration was given in Ref.[51].

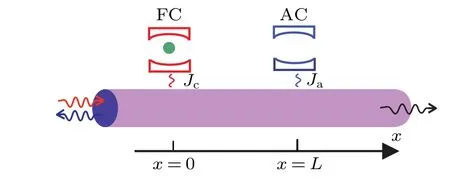
Fig. 1. The configurations of AC-assisted controlling single photon propagation. The FC and AC are coupled indirectly by a waveguide.The green dot denotes the two-level system.

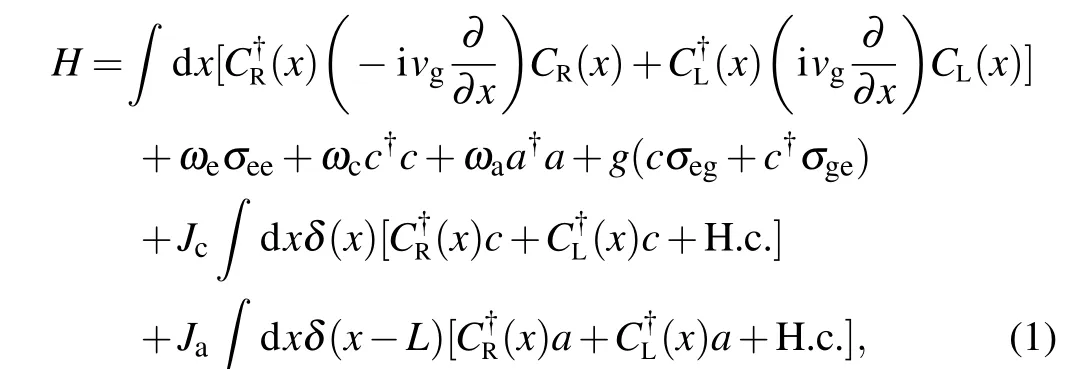
After linearization of the photonic dispersion of the waveguide mode near the eigenfrequency of the FC, the system can be described by the following Hamiltonian (with¯h=1):whereφR(x) andφL(x) are the probability amplitudes of the right and left propagating photon,respectively;|0〉denotes the vacuum state with the atom in the ground state and zero photon among the waveguide, the FC and the AC;ucanduaare the excitation amplitudes of the FC and AC modes, respectively;andueis is the excitation amplitude of atomic state|e〉.

For the single photon incident from the left of the waveguide,φR(x)andφL(x)take the form

whereθ(x) is the unit step function withθ(0)=1/2;tandrare the transmission and reflection amplitudes,respectively;aθ(x)θ(L−x)andbθ(x)θ(L−x)represent the wave functions of the single photon located between 0 andL.

From the eigenvalue equationH|Ψ〉=ω|Ψ〉,finally,one can obtain

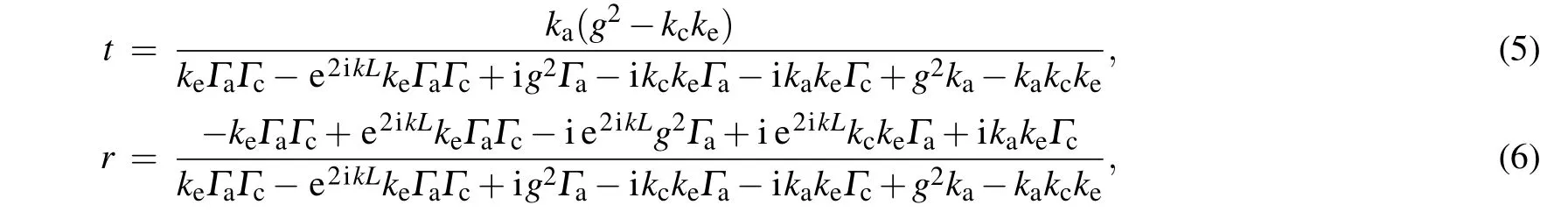
2.1. Without atom

Let us consider the simpler scenario of no atom embedded in the FC first. Then Eqs.(5)and(6)degenerate into

The results are the same as those of two emitters coupled in a one-dimensional waveguide. The transmission amplitude reaches zero atka=kc= 0, i.e.,ω=ωr1=ωaandω=ωr2=ωc. The locations of peaks (LP) in the transmission spectrum can be found when the following equations are satisfied,

The LPs are strongly dependent onkLdue to waveguidemediated dipole-dipole interaction between the two cavities.A symmetric transmission spectrum appears whenkL=nπ/2 withωa=ωcandΓa=Γc, wherenis an integer. WhenkL/=nπ/2,the transmission spectrum shows Fano-type transmission with strong asymmetry. We have analyzed the physical mechanism for the asymmetric Fano-type transmission spectrum.[19]Whenωa/=ωcwithkL=nπ, there is a transparency window in the transmission spectrum which is located atω=(ωa+ωc)/2.In this paper,we further discuss the effect of AC on the LP of the transparency.

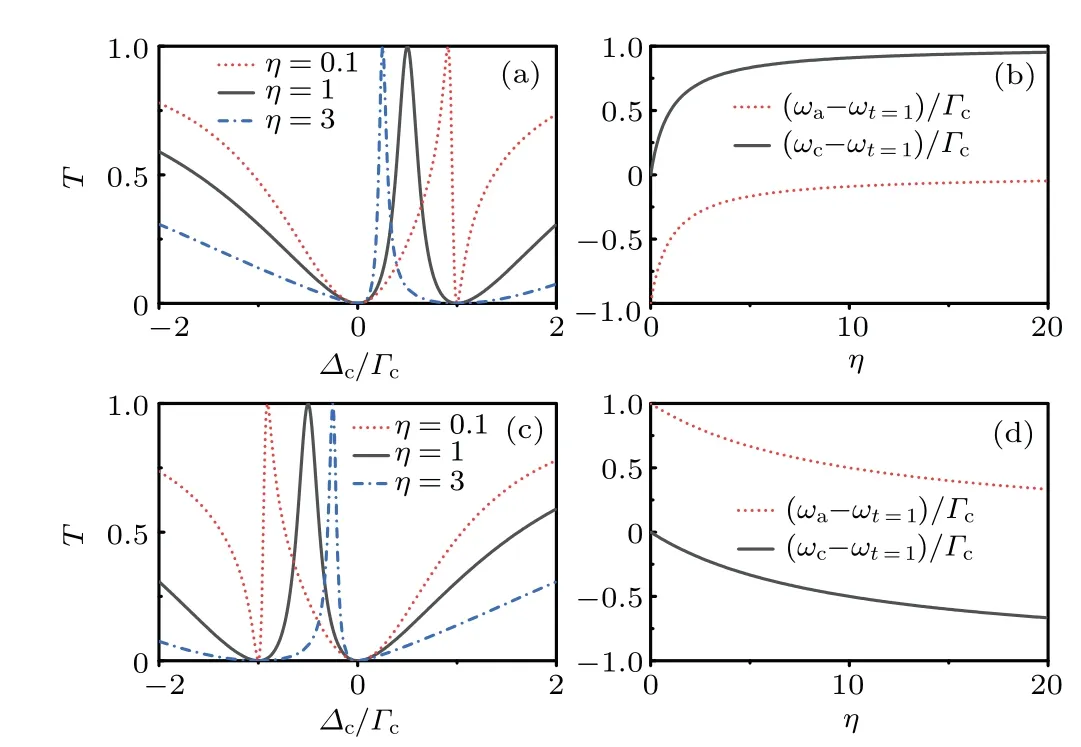
Fig. 2. Single photon transmission spectra (a) and (c) with different η. (b) and (d) The distance between the Fano dips and the LP. In (a)and(b),ωa −ωc =Γc,while in(c)and(d),ωa −ωc =−Γc. The other parameters are Γc=10−5ωc,kL=π.

It is not difficult to find thattreaches unit whenω=ωt=1≡(ωcΓa+ωaΓc)/(Γa+Γc) withωa/=ωcandkL=nπ.Hereωt=1depends strongly onΓaandωa. Thus,by adjusting the AC, one can obtain the scattering transparency window.Figure 2(a)showsT ≡|t|2as a function ofΔc=ω −ωcwith differentη, whereη ≡Γa/Γc. It shows that the peak shifts from a value close toωato a value close toωcwith increasing ofΓa. As we discussed above,there are two dips located atωaandωcin the transmission spectrum, respectively. The transmission spectrum is symmetric with respect to (ωa+ωc)/2 whenΓa=Γc. However,whenΓa/=Γc,the transmission spectrum exhibits strong Fano-type, as shown by the dotted lines and dashed dotted lines in Fig. 2(a). The LP is also shifted.Figure 2(b)shows the distance between the LP andωa(ωc). It exhibits clearly that the peak gets close toωcwith increasingη. The Fano line type nearωcshows strong asymmetry whenηis large. Figures 2(c)and 2(d)showTandωa(ωc)−ωt=1,respectively,for the case ofωa−ωc=−Γc. One can find that one of the dips shifts to−Γcdue to changing ofωa. It is noted thatωa−ωt=1becomes to be negative whenωc−ωt=1is positive. However, with increasingη, the peak still gets close toωc.

By carefully analyzing Eqs. (9) and (10), one can find a peculiar solution withω=ωt=1=ωc+Γcunder the condition thatkL=nπ −π/4 andΓa+ωa=Γc+ωc(ωa/=ωc). Figure 3 exhibitsTas a function ofΔcwith differentωa. It reaches unit atωc+Γc, which is consistent with the analytical analysis. There are still two dips in the transmission spectrum.One of the dip shifts due to differentωa. However, the other dip keeps at zero sinceωcis fixed. Different from the case ofkL=nπ,the Fano line-type betweenωcandωc+Γcis almost the same even thoughΓais different.

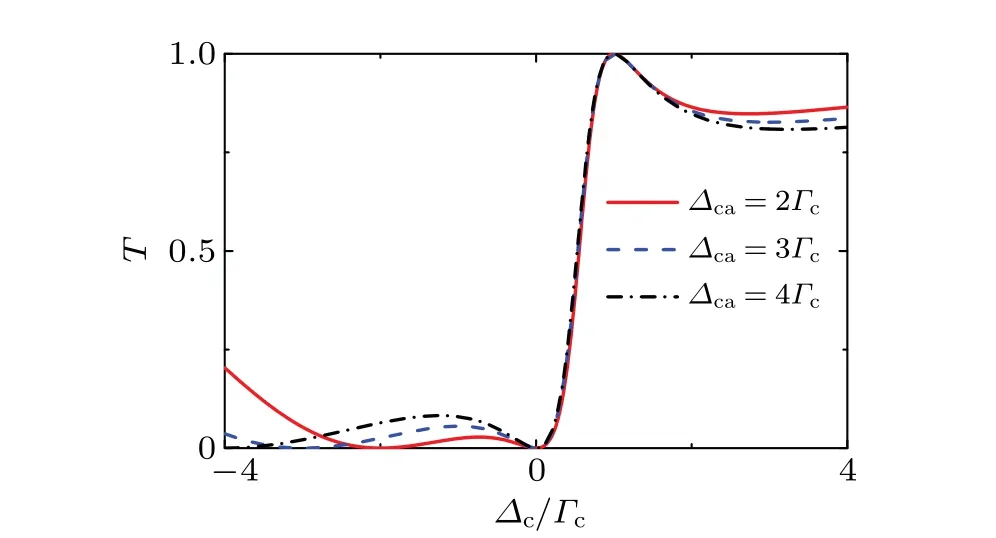
Fig. 3. Single photon transmission spectrum with different ωa. In the calculations, Γa+ωa =Γc+ωc, Γc =10−5ωc, kL=3π/4, Δca ≡ωc −ωa.

2.2. With atom

Now,let us consider the case in which an atom is embedded in the FC.By carefully analyzing Eq.(5),one can find that there are three dips in the transmission spectrum,which locate at

To explain this, we review the single photon scattering properties in the one-dimensional waveguide coupling to a twolevel system firstly. In such a system, the incident photon is reflected back with probability of 100% when it is resonant with the two-level system, and the two-level system is called“quantum mirror”. In our model,the AC can be equivalent to a two-level system. Thus, when the incident photon is resonant with the AC,i.e.,ω=ωa, it will be reflected back. The other two peaks of reflection spectrum result from the interaction between the FC and the atom. The system composed of FC and a two-level atom can be treated by using the dressed state picture. In the dressed state, one can get two eigenfrequencies,which are given byωr2andωr3,respectively. Thus,the incident photon with frequencyωr2(ωr3)will be reflected back with probability of 100%.

The LPs in the transmission spectrum can be determined by the following two equations:

Fig. 4. Single photon transmission spectrum with different η for the FC embedded within an atom. (a) The FC, AC and the atom are resonant with ωa =ωc =ωc. (b) The atom and the FC are non-resonant with ωe=ωc −Γc and ωa=ωc. In the calculations,Γc=g=10−5ωc,kL=π.

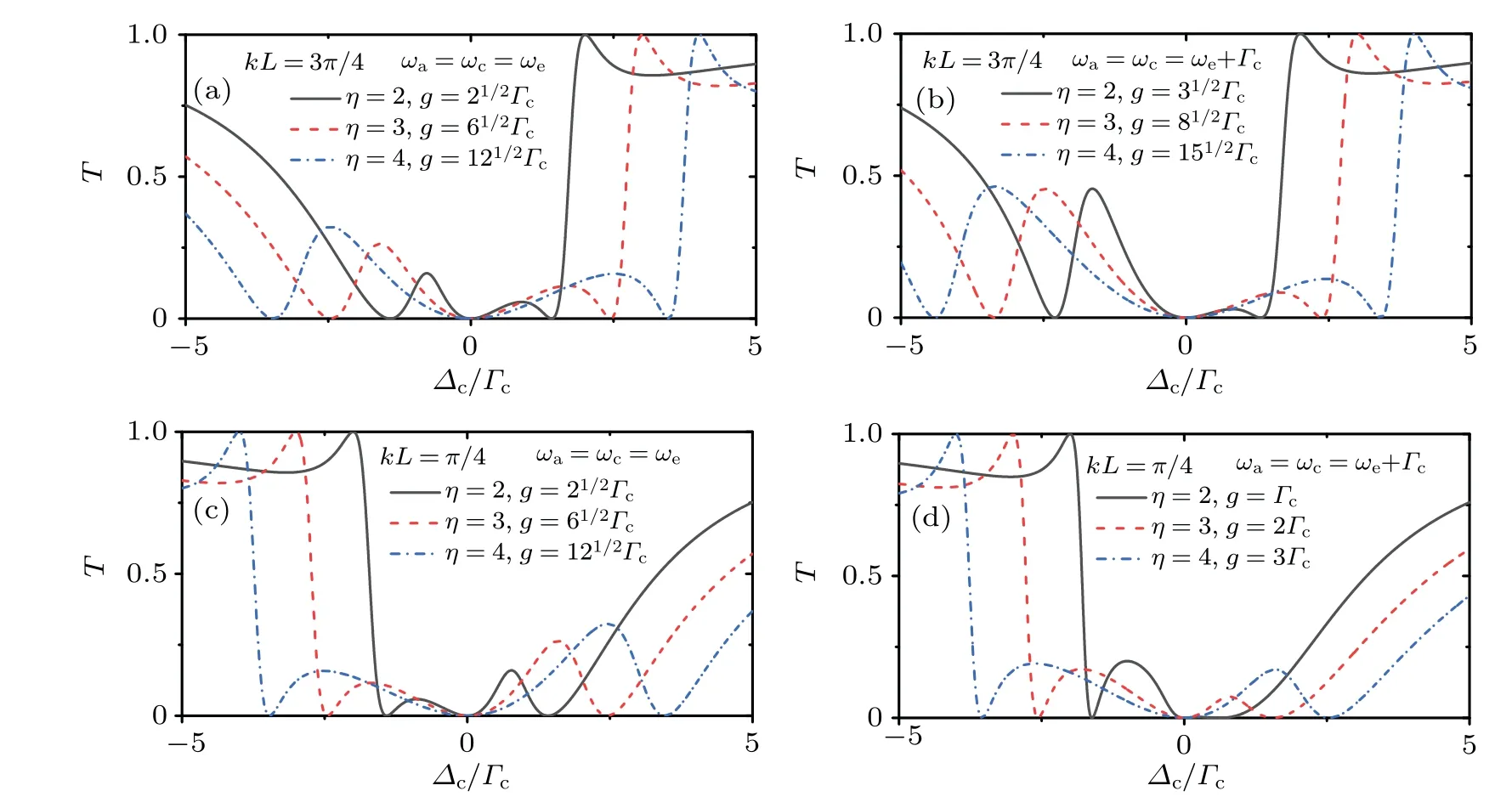
Fig.5. Single photon transmission spectrum for the FC embedded within an atom. In(a)and(c), the FC,AC and the atom are resonant. In(b) and (d), the FC and the AC are resonant but the atom is detuned with ωc −ωe =Γc. The other parameter in the calculations is given by Γc=10−5ωc.

3. Discussion

The Fano interference effects due to absorption and emission from the two or more emitters coupled to one waveguide have been discussed before.[19,37]The case ofkL=nπis studied widely in these reports. In the present article, we discuss analytically the dips and positions of peak in the transmission spectrum in detail and find that when no atom is embedded in the FC, there exists a transparency window withkL= (n −1/4)π. When an atom is embedded in the FC,there exists two transparency windows withkL=πand one transparency window withkL=(n±1/4)πin the case that FC and AC are resonant. The intrinsic physical mechanism results from energy structure modifications of the FC by the embedded atom. The locations of Fano dips and Fano-types can be modulated by the AC.

4. Summary

In summary, we have theoretically investigated Fano interference and transparency in a waveguide-nanocavity hybrid system with an auxiliary cavity.When no atom is embedded in the FC,there is a transparency window locating at(ωa+ωc)/2 withkL=πunder the condition ofωa/=ωc. Furthermore,we also find that whenkL=(n −1/4)π, a transparency window will appear under the conditionΓa+ωa=Γc+ωc. The locations of Fano dips are determined byωaandωc. When one atom is embedded in the FC,the locations of transparency windows depend on the coupling strength between the AC and the waveguide for the case ofkL=π. Comparing with the case of no atom embedded in the FC,there are transparency windows in the transmission spectrum whenkL=(n±1/4)π.The Fano dips depend strongly onωa,ωcandg. With increasingΓc,the Fano line-type near the transparency window becomes more sharp. Our results may find applications in designing quantum devices at single-photon level such as sensing,and single photon switching.