Detection of spin current through a quantum dot with Majorana bound states∗

Ning Wang(王宁), Xingtao An(安兴涛), and Shuhui Lv(吕树慧)

School of Sciences,Hebei University of Science and Technology,Shijiazhuang 050018,China

Keywords: Majorana bound states,quantum dot,spin current,Green’s function

1. Introduction

Majorana fermions (MFs) are a special type of particles which are their own antiparticles and obey non-Abelian statistics.[1]They have attracted a great deal of attention due to their fundamental importance and potential applications in the quantum computation.[2,3]In contrast to ordinary quantum computations, quantum computations using MFs do not require quantum error correction since a widely separated pair of MF bound states are immune to local sources of decoherence due to their nonlocal topological nature.[4]

Initially, Majorana bound states (MBSs) can be realized at the ends of one-dimensional quantum wire by inducing superconductivity on semiconductor wire with strong spin–orbit coupling and subject to an external magnetic field.[5–7]So far, many different schemes to create MBSs have been proposed and implemented, such as magnetic atoms on the surface of superconductors[8,9]and topological Josephson junctions.[10–12]But most experimental reports about the existence of MBSs focus on the nanowire setup.[13–16]Several suggestions have been made to detect and verify the existence of MBSs by different transport signatures. The differential conductance at zero bias voltage ise2/hwhen tunneling into a quantum dot(QD)side-coupled to MBSs.[17,18]Other suggestions include 4πperiodic Majorana–Josephson currents[19,20]and Majorana–Josephson interferometer.[21]Recently, some works mainly focus on the signatures associated with spin in electrical transport through a Majorana nanowire.[22,23]

In this paper, we investigate the spin and the charge currents of the system when the QD is side-coupled to MBSs driven by a symmetric dipolar spin battery.We find that MBSs have a great effect on spin transport properties. With the increase of the coupling strength between the MBS and the QD,the peak-to-valley ratio of the spin current decreases. And a non-zero charge current with two resonance peaks appears in the system. Furthermore, the coupling strength between the two MBSs weakens their effects on the currents of the system.

This paper is organized as follows. In Section 2, we present the Hamiltonian of our system and detail the algebraic expressions of the current obtained by the nonequilibrium Green’s function. The numerical results and analysis are given in Section 3.Finally,conclusions are drawn in Section 4.

2. Model and formula

In this section, we first present the setup of our system,as shown in Fig. 1. In Fig. 1(a), a QD is side-coupled to a topological wire hosing two MBSs driven by a symmetric dipolar spin battery. The MBSs emerge at two ends of the nanowire which is engineered by applying a strong magnetic field along its axis in proximity to an s-wave superconductor. Due to the proximity effect of the s-wave superconductor,the nontrivial superconductor phase resembles the p+ip superconductor phase that has two separated MBSs at two ends of the nanowire. In Fig.1(b),a QD is side-coupled to normal spin-polarized fermions.functions formalism, the electron currentJσfor spin componentσcan be calculated by the following standard formula:

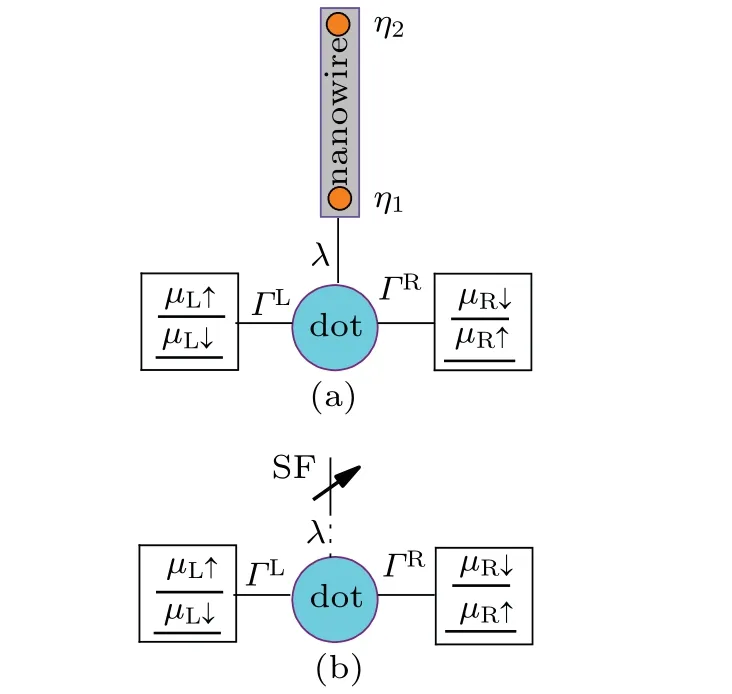
Fig. 1. Illustration of the proposed structure. (a) A QD coupled to a symmetric dipolar spin battery and side-coupled to a topological superconductor wire hosing two MBSs, η1 and η2. (b) A QD coupled to a symmetric dipolar spin battery and side-coupled to normal spinpolarized fermions.

3. Numerical results and discussion

In the numerical investigation, we consider the case of symmetric barriers withΓL=ΓR=Γ/2,Vs=0.5,U=12,and choose the line-width functionΓas the energy unit. Figure 2 shows the spin currentJs, the charge currentJeand the spin-polarized currentJσas a function of the dot levelεdwith various dot–MBS couplingλforεM=0 andVZ=0.

As we know,in the absence of the topological superconductor wire and MBSs (i.e.,λ=0), the spin current has two sharp resonance peaks atεd=0 andεd=−U,which are two possible conducting channels for tunneling through the QD,as shown by the black solid line in Fig.2(a). The energy separation between the two peaks is just the Coulomb interaction energy of the QD.The spin polarization current is with the opposite direction and the same amplitude,resulting in zero charge current,as shown by the black solid line in Fig.2(b).When the QD is side-coupled to the MBS(i.e.,λ/=0),the spin current in the non-resonance peak range increases asλincreases. Although the magnitudes of the spin current at resonance peaks are suppressed, they remain constant withλincreasing, as shown in Fig.2(a). The reason is that only the spin-down electrons are coupled to the MBS.The peak-to-valley ratio of the spin-down currentJ↓decreases asλincreases,but the spin-up currentJ↑is weakly dependent onλ, as shown in Figs. 2(c)and 2(d). According to the expressions of the spin current and the charge current, it can be found that the effect of the MBS on the spin current is mainly in the non-resonance range.Moreover,a non-zero charge current with two resonance peaks appears in the system,and it also increases asλincreases.

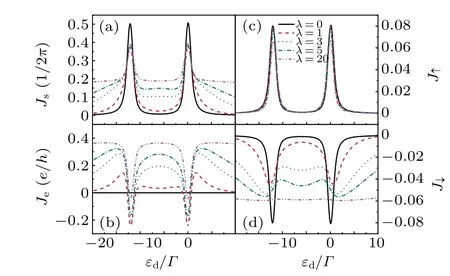
Fig. 2. The spin current Js (a), the charge current Je (b), the spinpolarized currents J↑(c) and J↓(d) as a function of the QD level εd with different dot–MBS coupling strength,εM=0 and VZ=0.

Furthermore, we compute the limiting case,λ=20. As shown in Figs.2(c)and 2(d),J↑is only slightly suppressed,butJ↓remains almost constant. As a result, the spin current and the charge current in non-resonance peak range are constants,as shown in Figs.2(a)and 2(b).

In order to clarify the genuine effect of the MBS,we calculate the current when the QD is coupled to normal spinpolarized fermions. Figure 3 shows the spin and the charge currents as a function of the QD energy when the QD is coupled to normal spin polarization fermions under the same configuration. The coupling energy for spin polarization and the Zeeman energy for the QD are both set to zero withεM=0 andVZ=0.

In Fig.3(a), we can find the resonance peaks of the spin current are suppressed, but they remain at the same position,when the QD is coupled to normal spin polarization fermions.With the increase ofλ,the spin current is weakly dependent on it. For the charge current,it is strictly zero whenλ=0;whileλ/=0, there are two negative peaks atεd=0 andεd=−U,as shown in Fig.3(b). It means that the spin-up electrons are more likely to be localized in the QD.

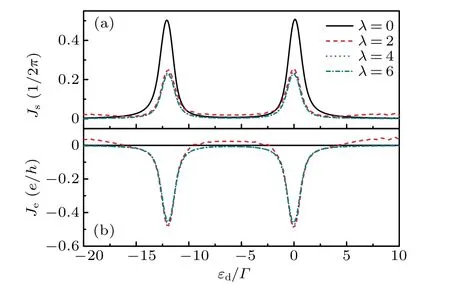
Fig.3. The spin current Js (a)and the charge current Je (b)as a function of the QD level εd with different dot–MBS coupling strength when the QD is coupled to normal spin polarization fermions with εM=0 and VZ=0.

It is well-known that there are three necessary conditions for the induction of MFs at both ends of nanowire:strong Rashha spin–orbit coupling,proximity-induced s-wave superconductivity and magnetic field. Because the QD and nanowire can be different materials and have differentgfactors,the Zeeman splitting energy induced by magnetic field in nanowire is different from that in the QD.Next,we study the effect of the Zeeman splitting energy in the QD on the system.

Fig. 4. The spin currentJs(a), the charge currentJe(b), the spinpolarized currentsJ↑(c)andJ↓(d)as a function of the QD levelεdwith different Zeeman energyVZwhen the QD is coupled to MBS,λ=2.

In Fig.4,we plot the spin current,the charge current and the spin polarized currents as a function of the QD levelεdforλ=2, with different values ofVZ, when the QD is coupled to the MBS. AsVZincreases, the two resonance peaks move towards the lower energy, and the distance between the two resonance peaks remains constant. Meanwhile,the resonance peak at the higher energy is suppressed. The characters are similar to the case of the QD coupled to normal polarization fermions,as shown in Fig.5. When the QD is coupled to the MBS,it is interesting that the resonance peak at the higher energy appears one shoulder atεd≈VZ. WhenVZis larger thanλ,the shoulder changes into a peak atεd≈VZ. The reason is that the resonance peak of the spin-polarized currentJ↓moves towards the higher energy and its range widens as the Zeeman energyVZincreases,as shown in Fig.4(d).

We also calculate the spin current and the charge current under different Zeeman energy for the QD coupled to normal polarization fermions, as shown in Fig.5. Different from the case of the QD coupled to the MBS,both the spin current and the charge current move towards the lower energy as the Zeeman energyVZincreases, and the distance between the two resonance peaks remains constant. However,with the increase of Zeeman energy,the amplitude of the resonance peak at the higher energy is suppressed,and that at the lower energy is increasing. Furthermore, the charge current is always negative.That is also different from the case of the QD coupled to the MBS in which the charge current can be positive or negative.

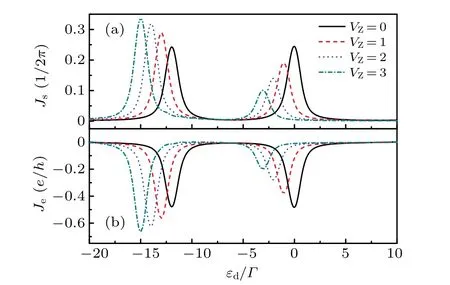
Fig.5. The spin current Js(a)and the charge current Je(b)as a function of the QD level εd with different Zeeman energy VZ when the QD is coupled to normal spin polarization fermions,λ =2.

In practice,the length of the nanowire cannot be so long that there is no interaction between the MBSs at both ends of the nanowire, so we calculate the effect of the coupling strength between the two MBSs on the electrical current. Figure 6 shows the spin current and the charge current as a function of the QD energy with different MBS–MBS coupling strengthεM.

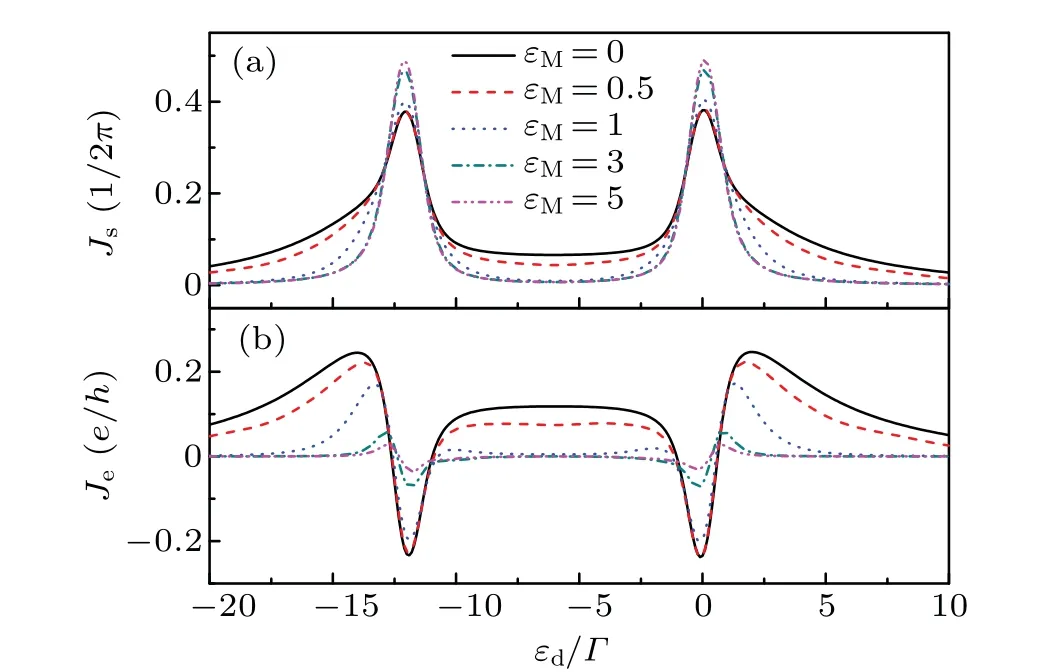
Fig.6. The spin current Js (a)and the charge current Je (b)as a function of the QD level εd with different εM when the QD is coupled to the MBS.The other parameters are VZ=0,λ =2.

As shown in Fig. 6, the magnitude of the two resonance peaks of the spin current increases withεMincreasing. Their positions remain the same,and their widths become narrower.The absolute value of the charge current decreases withεMincreasing,and the charge current may decrease to absolute zero when it is large enough. Comparing Figs. 2 and 6, it can be found that the spin current and the charge current return to the case ofλ=0 in Fig.2 withεMincreasing. That is to say the interaction between MBSs cancels out the interaction between the QD and the MBS.Therefore,in order to enhance the effect of the MBS on the system,εMshould be small enough.

4. Conclusion

In this paper, we have studied the spin transport properties of the QD side-coupled to MBSs driven by a symmetric dipolar spin battery. The MBSs can be emerged at two ends of one-dimensional quantum wire which is in proximity to ans-wave superconductor with strong spin–orbit coupling and subjected to an external magnetic field. Since the MBSs only interact with the spin-down electrons in the QD,the spinup polarization current is weakly dependent on the coupling strength between the QD and the MBS,and the peak-to-vally ratio of the spin-down polarization current decreases as the coupling strength increases. This causes the spin current to increase as the coupling strength between the QD and the MBS rises,except for the positions at the two resonance peaks.So is the charge current. Furthermore, it is found that the coupling strength between the two MBSs weakens their effects on the system.