犹豫模糊语言后悔理论和ELECTRE决策方法及应用

惠 蕙，王秋萍，李苗苗

西安理工大学 理学院，西安 710054

由于决策问题日益复杂化，决策者常选择用语言术语来表达看法及意见，并且可能会在不同的语言术语之间犹豫不决，为此，2012年，Rodríguez等人[1]提出了犹豫模糊语言术语集（HFLTS）的概念。Liao等人[2]给出了HFLTS的数学定义，并用犹豫模糊语言元素（HFLE）来表示语言变量的犹豫模糊语言值。HFLTS的语言表达模型使人类的思维和认知相一致，它允许不确定性、模糊性和犹豫性，可以灵活地表达决策者的认知复杂信息，引起了诸多学者的关注。因此有必要研究犹豫模糊语言环境下的多属性决策问题。

人们在现实决策活动中由于信息不完全、认知受限和时间压力而表现为有限理性。因此，作为描述人们有限理性行为的前景理论，被广泛应用于解决多属性决策问题[3]。前景理论考虑决策者的心理特征和风险态度，然而，在实际决策过程中，决策者不仅会感知风险，而且当知道自己未选择最佳方案时也会感到后悔。因此在考虑决策者心理行为的情况下，决策者的行为应基于风险厌恶和后悔规避。Bell[4]、Loomes和Sugden[5]分别提出的后悔理论是一种行为决策理论，其综合考虑到在行为决策分析中出现的后悔和欣喜两种不同的心理感受，被认为是最广泛和流行的有限理性的行为决策模型之一。与前景理论相比，后悔理论可以有效地处理后悔规避行为，而且不需要决策者事先给定参考点，计算公式中的参数相对较少。近年来，许多学者将后悔理论引入模糊决策环境中。文献[6]提出一种基于后悔理论的犹豫模糊信息决策方法。文献[7]将后悔理论应用到直觉模糊信息的环境中，并通过网络游戏的案例说明其方法的可行性。文献[8]提出一种基于后悔理论的区间灰数多准则决策方法。

ELECTRE方法[9]是最具代表的级别高于方法，因为ELECTRE III引入了严格优于阈值、无差异阈值和否决阈值来表示专家判断的固有不确定性，所以ELECTRE III在ELECTRE方法族中发挥着突出的作用。由于ELECTRE III在处理不精确信息和部分补偿效果方面的有效性，因此ELECTRE III法在实际决策问题中受到广泛的关注。文献[10]构建了基于ELECTRE III的农户小额贷款企业信用评级决策模型。文献[11]采用Z数、后悔理论和ELECTRE III相结合的决策方法，以评估新能源投资风险问题。文献[12]提出了一种基于ELECTRE III方法处理认知复杂信息为犹豫模糊语言术语集的多专家多准则决策问题。

文献[13]给出了一种犹豫模糊语言的多属性决策问题方法，数据产品服务商选择实例说明犹豫模糊语言在表达复杂信息时的灵活性和可行性。后悔理论被广泛应用于解释一些期望效用理论不能解释的“悖论”或“异象”[8]，为多属性决策问题提供了新方法，ELECTRE III能反映决策者关于属性间的部分可补偿性。如何将后悔理论与ELECTRE III结合应用到犹豫模糊语言信息下的多属性决策问题，是一个值得研究的问题。根据以上分析，本文针对属性权重未知的犹豫模糊语言多属性决策问题，利用灰色关联分析与极大熵结合确定犹豫模糊语言信息下的属性权重，进而提出了一种基于ELECTRE III与后悔理论结合的犹豫模糊语言多属性决策方法。

1 基本概念

1.1 犹豫模糊语言术语集

定义1[2]设X为一论域，x i∈X,i=1,2,…,N,S=是一个语言术语集，X上的一个犹豫模糊语言术语集H S可表示为：

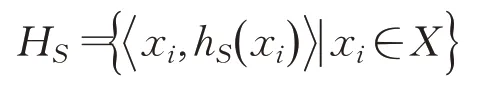
其中，h S()x i是语言术语集S中的一列可能的取值，可以表示为：

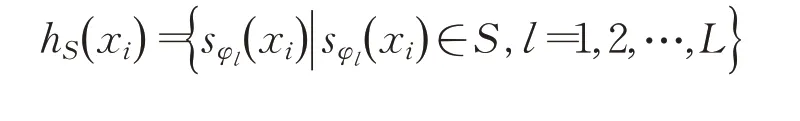
其中，L是h S(x i)中语言术语的个数，h S(x i)表示语言变量x i对语言术语集S的可能的隶属程度。称h S(x i)为犹豫模糊语言元素，而H S是所有犹豫模糊元素的集合，h S(x i)、sφl(xi)简写为和。

定义2[14]设是一个语言术语集是犹豫模糊语言元素，L是语言术语的数量，的犹豫度定义为：

文献[2]中给出了犹豫模糊语言元素的汉明距离公式：

本文考虑犹豫模糊语言元素的犹豫度，在文献[2]的基础上，定义两个犹豫模糊语言元素的距离如下：

定义3设和是S上的任意两个犹豫模糊语言元素，定义和的包含犹豫度的规范化汉明距离为：

定义4[15]设S={s t|t=-τ,…,-1,0,1,…,τ}是一个语言术语集，h S={sφl|sφl∈S,l=1,2,…,L} 是犹豫模糊语言元素，h S的得分函数和方差函数为：

注意：在大多数情况下，不同的HFLE有不同数量的语言术语。因此，为了计算时正确操作，一般通过添加语言术语来扩展元素个数相对少的HFLE，直到它们有相同的元素个数[15]。本文通过添加中间的语言术语项来扩展元素个数较少的HFLE。

1.2 后悔理论

根据后悔理论可知，决策者将选择方案的结果与其他方案的结果进行比较，以衡量决策者的欣喜和后悔水平，并选择决策者不会后悔的最佳方案。若选择其他方案会带来更好的结果，则决策者会感到后悔，反之则欣喜，由于决策者心理行为特点是后悔规避的，那么两方案相互比较的后悔-欣喜函数R()Δu单调、递增、凹的，可表示为[6]：其中，μ>0表示决策者的后悔规避系数，μ越大表示后悔规避程度越大，Δu表示两方案效用之差，本文采用文献[6]的效用值：

基于式（5）和式（6）确定欣喜函数为[11]：

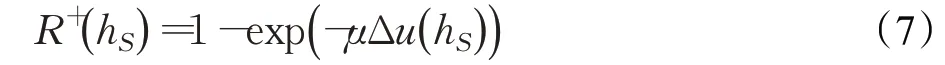
后悔函数为：

2 基于后悔理论的犹豫模糊语言ELECTRE法

设犹豫模糊语言多属性决策问题中，A={A1,A2,…,A m}为备选方案集，C={C1,C2,…,C n}表示属性集，W=(ω1,ω2,…,ωn)表示属性权重向量，并且满足。设表示决策者对备选方案集A在属性集C下的决策矩阵，其中表示决策者对备选方案Ai在属性C j下的犹豫模糊语言评价信息值。

2.1 属性权重的确定

文献[16]在区间灰数的环境中利用灰关联与极大熵结合确定属性权重，本文将该方法拓展到求解犹豫模糊语言环境下的属性权重。在决策信息评价矩阵中，属性元素之间的内在关联性意味着属性之间的关联信息的存在，一定程度上反映了不同属性元素之间不同的相对重要程度。首先构造理想参考序列，以求得各对比序列与参考序列在各个属性下的关联系数。设犹豫模糊语言参考序列为正理想解：

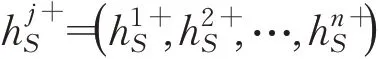
其中，ξ为分辨系数，一般地，取为0.5。

根据极大熵原理，使权重熵值达到最大，并且满足约束条件得到的权重值比较合理[16]。基于极大熵准则，结合灰色关联系数，建立的极大熵模型为：

2.2 级别高于赋值方法

文献[11]根据ELECTRE III的规则提出了一种Z数信息下的级别高于赋值方法，这里给出犹豫模糊语言信息下的级别高于赋值方法。首先，给出了基于欣喜函数和后悔函数的犹豫模糊语言元素的和谐指数与不和谐指数。然后，给出了方案A i优于A k的可信度指数。最后，为方案制定了排序规则。

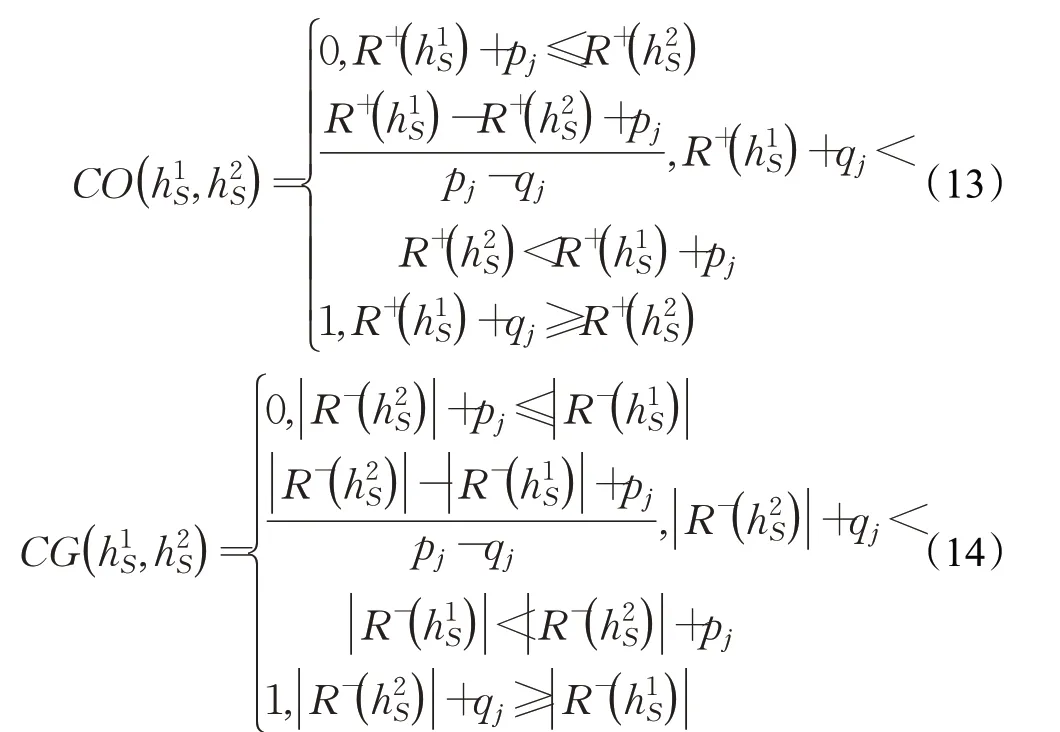
优于的欣喜不和谐指数和后悔不和谐指数分别为：

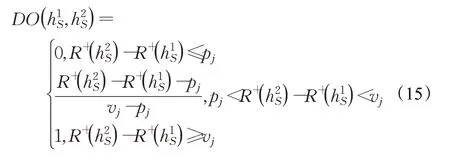
有序方案对(A i,A k)的和谐指数CC(A i,A k)为：

当C j(Ai,A k)为欣喜和谐指数CO j(Ai,A k),CC(A i,Ak)就为欣喜和谐指数CCO(A i,A k)；当C j(A1,A2)为后悔和谐指数CG j(Ai,A k)，CC(A i,Ak)就为后悔和谐指数CCG(A i,A k)。CC(Ai,A k)表示支持“Ai级别高于A k”这一论断的测度，D j(A i,A k)表示拒绝“Ai级别高于A k”这一论断，即不和谐性强度的测度。

方案Ai优于Ak的可信度指数R()A i,Ak定义为：

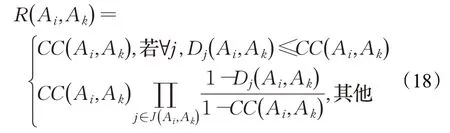
其中，J(Ai,A k)是所有D j(Ai,A k)>CC(A i,Ak)的属性的集合。同样，当C C(A i,Ak)和D j(A i,Ak)是后悔或欣喜指数，R(A i,A k)就为后悔或欣喜的可信度指数。

设RG(A i,A k)和RO(Ai,A k)分别为Ai优于A k的后悔和欣喜可信度指数，RG(A k,Ai)和RO(A k,A i)分别为A k优于Ai的后悔和欣喜可信度指数，则方案A i优于A k的可信度指数ψ(A i,Ak)为：

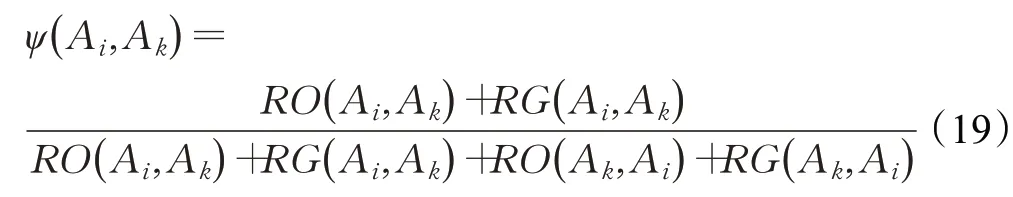
2.3 方案净可信度的确定

通过引入一致可信度，非一致可信度以及净可信度为ELECTRE III方法提供一种简单可靠的排序方法[10]。

（1）一致可信度的确定。

（2）非一致可信度的确定。

（3）净可信度的确定。

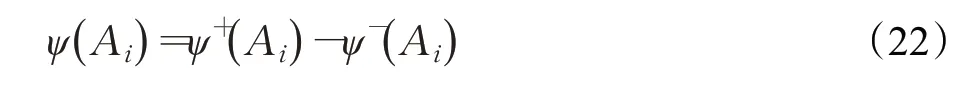
将各方案的净可信度根据降序排列，就能得到各方案由优到劣的综合排序。

2.4 决策步骤

步骤1根据决策者给出的决策信息构造犹豫模糊语言术语集决策矩阵

步骤2根据式（11）和（12）确定属性权重。

步骤3根据式（13）、（14）和（17）计算欣喜-后悔和谐指数。

步骤4根据式（18）计算欣喜-后悔可信度指数。

步骤5根据式（19）计算可信度指数。

步骤6根据式（22）计算净可信度ψ(Ai)，将ψ(A i)按降序排列，就可得到方案集由优到劣的排序。

3 算例分析

3.1 算例

本文算例来自文献[18]。糖酒会举办方要与一家最令人满意的住宿企业签订合作合同。其中三家酒店分别记为A1汉庭、A2锦江之星、A3如家。四个评价属性为地理位置与交通便利性C1、酒店的硬件设施和设备及服务水平C2、酒店的配套服务C3、酒店的价格C4。邀请专家对这三家酒店的四个方面分别进行评估，C1,C2,C3属于效益型指标，可用如下评估标度表示，S={st|t=-3,-2,-1,0,1,2,3},s-3=“非常差”,s-2=“很差”,s-1=“差”，s0=“一般”，s1=“好”，s2=“很好”，s3=“非常好”。C4属于成本型指标，评估标度如下，S={s t|t=-3,-2,-1,0,1,2,3}，s-3=“非常低”，s-2=“很低”，s-1=“低”，s0=“一般”，s1=“高”，s2=“很高”，s3=“非常高”。决策者给出的决策信息如表1所示[18]。

表1 决策信息Table 1 Decision information

由题设给出的评估标度可将表1转化为表2。

表2 决策矩阵Table 2 Decision matrix

决策步骤如下：

步骤1规范化决策信息。利用文献[18]所给出的方法，将成本型属性下的评估值转化为效益型属性下的评估值，如表3所示[18]。

表3 标准化决策矩阵Table 3 Normalized decision matrix

步骤2根据2.1节确定属性权重模型为：

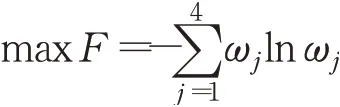
则根据模型解得属性权重为：

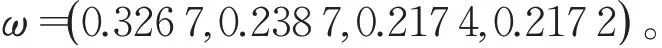
步骤3根据式（13）、（14）、（17）可得欣喜-后悔和谐指数，参数μ=0.3[6-7]。

依据文献[11]，取所有属性门槛值为q j=0.05，p j=0.2，v j=0.4。

那么欣喜和谐指数为：

后悔和谐指数为：

步骤4根据式（18）计算欣喜-后悔可信度指数分别为：

欣喜可信度指数：

后悔可信度指数：

步骤5根据式（19）计算可信度指数为：

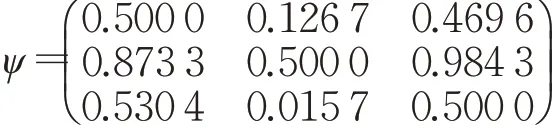
步骤6根据式（22）计算出的净可信度分别为：ψ(A1)=-0.807 3，ψ(A2)=1.715 2，ψ(A3)=-0.907 9，按降序排列即ψ(A2)>ψ(A1)>ψ(A3)，则A2≻A1≻A3。

为了考证参数μ的取值变化对最终决策结果的影响，这里给出μ在不同取值下的方案排序结果，如表4所示。由表4可以看出，结果对μ值不敏感，最优方案都是A2，只有当μ=0.4时方案A1和A3的排序发生了变化，表明了所提方法的稳定性。

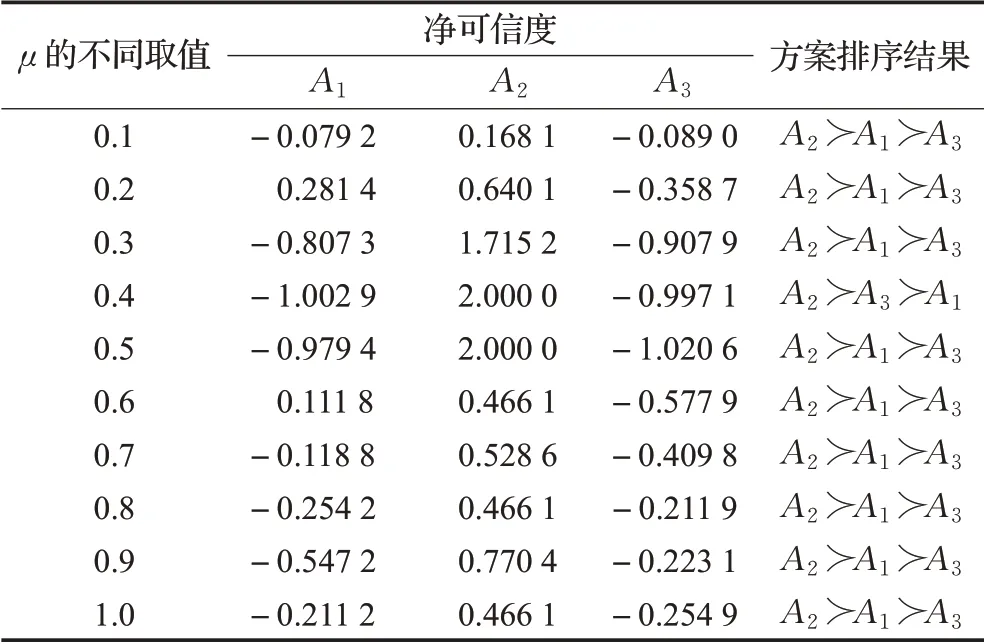
表4 不同μ值的决策结果Table 4 Results with differentμvalues

3.2 比较分析

为了验证本文方法的有效性，将所提出的方法与其他两种现有方法进行了比较，包括Loomes等人[5]提出的后悔理论法，以及文献[18]提出的基于犹豫模糊语言的前景理论决策方法。

（1）与文献[5]方法的比较

依据文献[5]的后悔理论可知在属性C j下选择方案Ai而没有选择方案A k，方案A i的感知效用函数为：

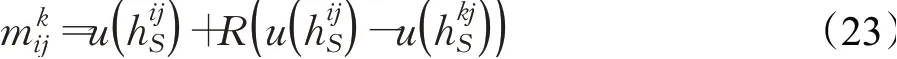
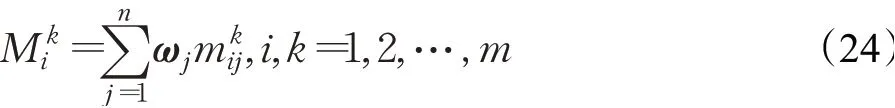
那么方案A i相对于其他方案的总体感知效用为：

其中，表示方案集A中每个方案Ak的权重。在本文中如文献[5]，取

首先计算在属性C j()j=1,2,…,n下方案两两比较的感知效用矩阵，当效用函数取式（6），后悔-欣喜函数取

然后由式（24）计算综合感知效用矩阵，其中属性权重为前面计算所得：

根据总体感知效用值可得方案的排序为A2≻A1≻A3。同理可得R(Δu)=1-0.8Δu[5]时方案的排序结果。表5给出本文方法与文献[5]方法在取不同的后悔-欣喜函数下方案的结果。

表5 本文方法与文献[5]方法的排序结果Table 5 Ranking results of method in this paper and method in references[5]

由表5可知，本文方法和文献[5]方法的方案排序结果一样，最佳候选酒店均为A2，但本文方法所得的最优方案与次优方案的排序值差异更大，这说明本文所提方法不仅可行，而且更令人信服。本文将后悔理论与ELECTRE III相结合，不仅可以考虑到决策者的后悔规避心理，还充分体现了属性间的部分可补偿性，使得决策结果更能反映实际情况。由于这些特性，所建立的模型在决策过程中可以有比其他方法更合理、更有效的结果。

（2）与文献[18]的比较

为便于比较，当距离公式采用式（2），属性权重：ω1=0.326 7,ω2=0.238 7,ω3=0.217 4,ω4=0.217 2时，应用文献[18]的方法，并根据文献[18]的参数α=β=0.88,γ=0.61,δ=0.69,λ=2.25对算例进行决策分析。

首先计算各方案在各属性下的前景值，见表6。其次，计算各方案在各属性下的心理权重，见表7。最后，得到各方案的综合前景值，见表8。并根据综合前景值排序。

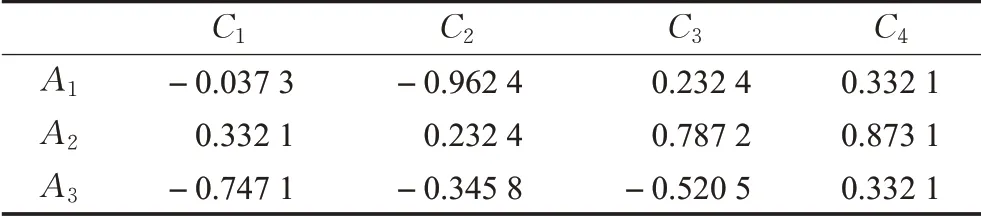
表6 各方案在各属性下的前景值矩阵Table 6 Matrix of prospect values for each alternative under each attribute

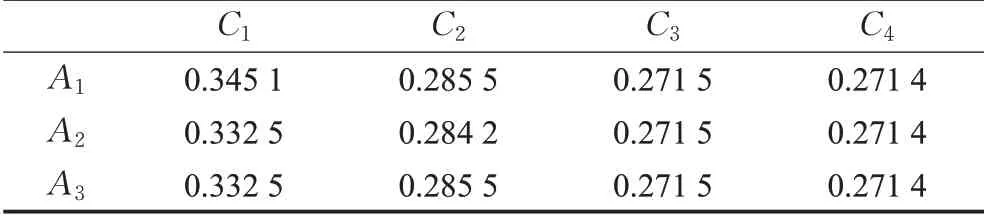
表7 各方案在各属性下的权重Table 7 Weight of alternative by attribute

由表8可知方案排序为A2≻A1≻A3，最佳候选酒店为A2。

表8 各方案的综合前景值Table 8 Comprehensive prospect value of each alternative

前景决策方法涉及五个参数分别为α、β、γ、δ、λ。0<α<1,0<β<1,α、β表示决策者的风险态度，取值越大，表明决策者越倾向于冒险；λ>1,λ表示损失规避程度，取值越大，表明决策者的损失规避程度越高；γ、δ分别表示心理预期为收益或损失时的风险态度系数。在文献[18]中，α=β=0.88,γ=0.61,δ=0.69,λ=2.25。Abdellaoui建议α、β分别取0.89和0.92[19]；Kahneman和Tversky建议λ的取值在2.0和2.5之间[20]；Tversky和Kahneman认为取γ=0.6，δ=0.72[21]；Richard和Wu认为取γ=0.74，δ=0.74[22]。

依据以上所述的参数取值情况，只改变一个参数，其他参数不变的情况下对算例进行决策分析。具体结果见表9。

由表9可知，前景决策方法中参数取15组值时，排序结果完全相同，当α=β=0.88,γ=0.61,δ=0.69,λ=2.5时，最优方案与次优方案的排序值差异更大。本文方法与前景决策方法的排序结果一致，且本文方法的决策结果区分度更高，即最优方案与次优方案的相对差异较前景决策方法更大。决策分析结果表明了本文所提方法的可行性和有效性。在具体的运算过程中，本文中后悔理论方法只需用一个参数来描述决策者的心理行为，计算相对简单，而文献[18]的前景决策方法需要五个参数，计算相对复杂。此外，后悔理论方法还考虑了决策者的后悔厌恶行为，这对于决策至关重要并且更贴近现实世界。因此，该方法可以综合考虑决策者的心理因素，并产生更合理的结果。

表9 本文方法与文献[18]方法的排序结果Table 9 Ranking results of method in this paper and method in references[18]

4 结语

犹豫模糊语言信息可以用来表达决策者在不确定环境下的评价信息，这种表达简洁灵活，能体现出决策者犹豫不决的心理，同时也保证了最终结果的合理性。本文在犹豫模糊语言环境下，提出了一种基于后悔理论和ELECTRE III相结合的多属性决策方法。本文的创新如下：（1）基于后悔理论提出犹豫模糊语言元素的后悔-欣喜函数，用来处理犹豫模糊语言信息，使得决策者的心理行为可以通过后悔和欣喜值来体现。（2）属性权重是决策过程中的重要参数，利用灰色关联分析与极大熵原理结合确定犹豫模糊语言信息下的属性权重，使得到的结果更加合理。（3）将ELECTRE III扩展到犹豫模糊语言信息环境下的多属性决策问题，利用ELECTRE III的规则给出了犹豫模糊语言信息下的级别高于赋值方法，充分考虑了属性间的部分补偿原则。

本文的算例结果说明了本文所提方法的可行性和有效性。与其他两种方法的比较讨论表明，本文方法所得最优方案比次优方案的区分度更大，排序结果更令人信服，进一步说明该方法的有效性。