考虑小干扰稳定性的风火打捆配比优化

王艺舒，蔡国伟，杨德友，王丽馨

（东北电力大学电气工程学院，吉林 132012）

随着以风电为代表的新能源技术发展日渐成熟，风力发电并网容量逐渐增加。在我国的“三北”地区蕴藏着丰富的风能资源，我国的陆上风电基地也主要分布在“三北”地区，这些地区用电负荷不高，风电难以就地消纳，而我国负荷中心主要集中在东南沿海等地区，这就造成了风能资源与电能需求的逆向分布。为解决上述难题，将风电、火电“打捆”联合外送[1-3]。风火打捆外送解决了我国风能资源与负荷中心逆向分布的问题，但同时给电力系统的稳定运行带来了新的挑战[4-5]。

关于风火打捆系统中的风火配比问题，文献[6]综合考虑系统成本和风火总输电电量提出了一种风火配比优化方法。文献[7]针对风火容量配比问题，综合考虑了建设成本、输电损耗和风电弃风量等因素，提出了风火容量优化分配模型。文献[8]考虑了风电不确定性并量化其带来的弃风限电风险，兼顾风电外送需求和系统弃风带来的风险，建立了风火打捆系统多目标优化调度模型。文献[9]结合扩展等面积法则并据此给出的暂态稳定判据提出了暂态稳定约束下的风火配比优化方法。

在大型电力系统中阻尼过低导致的系统低频振荡问题日益严重，关于风电并网对系统小干扰稳定性的影响，许多学者进行了深入研究。文献[10-11]研究了三种类型的风机对区间振荡模态的影响，发现增加风电穿透率能够改善系统小干扰稳定性。文献[12]推导了双馈异步风机DFIG（doublyfed induction generator）数学模型，采用特征值分析和时域仿真分析研究风电渗透率对系统阻尼的影响。结果表明风机接入可以增强系统的阻尼，但风电穿透率过高会恶化系统阻尼。文献[13]简化了风电接入后的系统状态矩阵，研究了风电比例对系统小干扰稳定性的影响，结果表明适当的增加风电出力能够提高系统小干扰稳定性。文献[14-16]研究了风电并网位置、并网容量等因素对电力系统机电振荡的影响，结果表明风电接入对系统区间振荡模态有正阻尼的作用。文献[17]认为风电机组代替同步机并网时会导致系统惯量降低，使系统阻尼增加，系统抑制功率振荡能力有所提升；比较了增加风电穿透率与减小系统惯量两种情况在不同联络线传输功率下对区间振荡的影响。

对于大型互联电网，系统区间振荡模式的阻尼比与区域间传输功率和系统惯量密切相关，小干扰稳定要求将会限制互联系统的区间传输能力[18-19]。研究风火打捆系统在小干扰稳定约束下的风电火电配比，对提高风火打捆外送能力以及确保系统稳定运行具有重要意义。本文研究了风火打捆系统小干扰稳定性分析方法，提出了含小干扰稳定性约束的风电与火电输出配比优化模型。通过风火打捆测试系统充分验证了所提出的风火配比优化方法的有效性和可行性。

1 风火打捆系统小干扰稳定性分析

对于如图1（a）所示的风火打捆互联系统，可将其化简为如图1（b）所示的等效两机系统。其中ASG1和ASG2分别是发电机组1和发电机组2的聚合同步发电机ASG（aggregated synchronous genera⁃tor）。是母线1和母线2的电压矢量；İi=Ii∠αi,i=1,2 是母线1和母线2的等效注入电流矢量；xl是母线1和母线2之间的等效电抗；Ėi=Ei∠δi,i=1,2 是 ASG1 和 ASG2 的 内 部 电 势 ；xi,i=1,2是ASG1和ASG2的内部电抗。

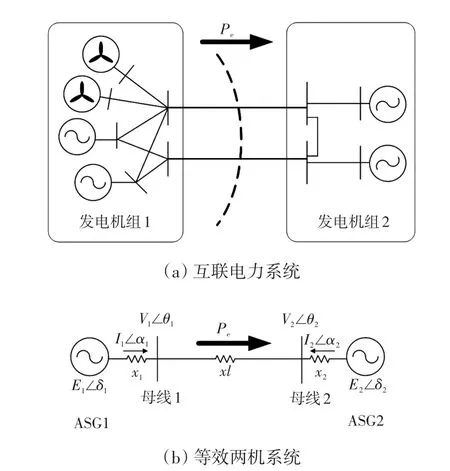
图1 互联电力系统单线图和简化系统Fig.1 Single-line diagram and reduced system of interconnected power system

在小干扰稳定分析中，主要使用转子运动方程描述系统的动态特性。两机等效系统的动态特性可由单机无穷大系统的转子运动方程来表示，即

式中：δ=δASG1-δASG2,ω=ωASG1-ωASG2分别为系统等效功率角和角速度；D为等效阻尼系数；HASG1和HASG2分别为发电机组1和发电机组2所在区域的等效惯性时间常数；Pm1和Pm2分别为发电机组1和发电机组2的机械功率，Pe为互联电网联络线传输功率。

在风火打捆系统中，对于由常规同步发电机和风力发电机组并联组成的送端或受端区域，其等效惯性时间常数为

式中：HSG,i、HWT,j、HASG分别为同步机i的惯性时间常数、风电机组j的惯性时间常数及区域电网的等效惯性时间常数；M、N分别为区域内同步机组和双馈风电机组的台数；SSG,i、SWT,j、Stot分别为区域电网内同步发电机组i、风电机组j及区域电网的额定容量。

根据式（4）可知，改变风火打捆系统中的风电火电容量配比，会导致风火打捆系统惯量发生变化，从而影响电力系统的动态稳定性。

对风火打捆系统进行小干扰稳定性分析，将式（1）和式（2）在平衡点处线性化，经拉普拉斯变换后的频域方程可表示为

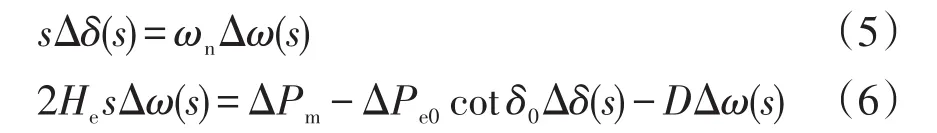
式中：s为拉普拉斯算子；Pe0和δ0分别为有功功率和功角的初始值。等效两机系统的特征方程可以表示为

2 风火配比优化

2.1 风火配比优化模型

本文的目的是在考虑小干扰稳定约束并保证风火打捆功率外送能力的前提下对风火打捆系统中风火配比进行优化。根据式（9）和式（10），可以将阻尼比表示为风火打捆外送功率和系统等效惯量的函数，即

以算例中风火打捆系统为例，改变风火配比令风火打捆送端系统等效惯量在87～117 s内取值。绘制如图2所示系统区间振荡特征值随联络线功率增加的移动轨迹。

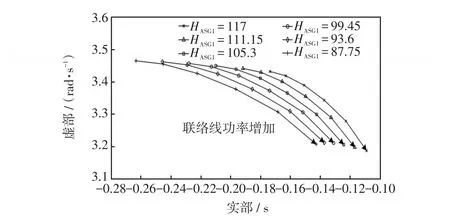
图2 特征值随联络线功率增加的移动轨迹Fig.2 Movement trajectory of eigenvalues with the increasing tie line power

对式（11）和图2进行分析可知，在风火打捆系统中，系统阻尼随联络线功率增大而减小，风火打捆外送功率对系统有“负阻尼”的作用。而风力发电机代替同步机时会降低系统的惯量，进而改善系统阻尼，双馈风机并网对系统有“正阻尼”的作用。选取适当的风火配比既可以满足小干扰稳定性要求又能够保证风火打捆外送能力。然而过多的风电代替同步机接入电网，将会降低系统整体的惯性支撑能力，影响频率稳定性，因此系统惯量不应过低，选取临界阻尼(ξcritical)作为风火配比的优化目标。使其同时满足式（12）和（13）中的F1和F2的最小值：

式（14）中λ是使阻尼比和有功功率具有相同数量级的经验系数。当区域间传输功率和系统惯量变化不大时，其对区间振荡模态频率的影响可以忽略不计。故假设改变风火配比前后的振荡频率为定值。

在进行风火配比优化时，保证风电火电的总出力PT不变，通过改变火电机组的启停状态并用等容量的风电机组并网代替停机的火电机组以改变风火配比。式（15）和式（16）中 PSG,i和 PWT,j分别为风火打捆系统中火电机组i和风电机组j的有功出力，δSG,i和δWT,j分别为火电和风电的出力率。目前，包括双馈型、直驱型的变速风电机组是风电场采用的主要机型，风机通过电力电子设备连接到电力系统，使得风机转速与系统频率解耦，并不能像传统的同步机那样对系统提供有效的惯性支撑。因此，双馈风机与直驱型风机并网后对系统惯性的贡献可以忽略不计，故取HWT为0。由式（4）可以得到送端系统在系统基准容量(Sbase）下的等效惯量HASG1的表达式如式（17）所示。假设系统中火电机组参数相同，可以得到系统中火电机组剩余开机数M，进而得到此时的风火配比，式（18）中表示向下取整数。为保证电力系统可靠运行并提高风火配比优化的计算效率，分别给出区间传输功率、等效功率角和系统等效惯量的约束，式（19）～（21）中：Pe、Pe,max、Pe,min分别为区间传输功率及其上、下限；δ、δmax、δmin分别为等效功率角及其上、下限；H、Hmax、Hmin分别为等效惯性时间常数及其上、下限。

根据式（12）～（21），对风火配比进行优化。由式（12）～（21）组成的优化模型是一个简单的低维模型，可通过适当的优化算法快速求解。同时，进一步精确变量的范围可以提高优化结果的精度并减小误差。

2.2 风火配比优化流程

目前，PMU已广泛用于电力系统中，安装在大容量发电厂、变电站和区域间联络线等电力设备上。利用PMU测量风火打捆系统的电压、电流、频率和相角等数据获得风火配比优化计算所需的基本参数。

如前文所述，考虑小干扰稳定性约束的风火打捆系统风火配比优化具体步骤如下：

步骤1 使用PMU测得的边界母线电压和电流估算系统等效功角。利用随机子空间（SSI）算法对所测得的系统环境数据进行辨识，提取系统机电振荡参数。

步骤2 利用遗传算法对所提出的考虑小干扰稳定性约束的风火配比优化模型进行求解。

步骤3 根据系统等效惯量H的优化结果计算风火打捆系统中火电机组剩余开机数，进而得到风电火电最优配比。

风火配比优化流程如图3所示。

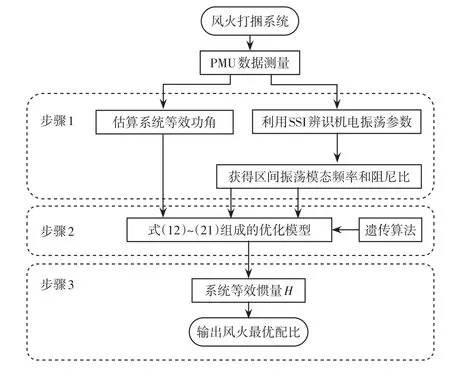
图3 风火配比优化流程Fig.3 Flow chart of wind-thermal capacity ratio optimization

3 算例分析

为验证本文所提出的风火配比优化方法的有效性，在DIgSILENT/PowerFactory中搭建的风火打捆系统如图4所示。

图4 风火打捆系统Fig.4 Wind-thermal bundled system

该系统基于IEEE 4机2区域系统拓扑结构，风电场在区域1中的母线6处并网，构成风火打捆交流外送系统。区域一中的发电厂G1为装机容量900 MW的同步发电机组，发电厂G2为10台装机容量为90 MW的同步发电单元并联组成；风电场由若干台装机容量为5 MW的双馈风电机组成。区域2中的发电厂G3和G4为两台容量900 MW的同步发电机组。区域1内发电功率为1 400 MW，区域1向区域2传输的有功功率为419 MW。

系统中各发电机组的额定容量、以各自额定容量为基准的惯性时间常数和在系统基准容量（100 MW）下的惯性时间常数如表1所示。

表1 风火打捆系统各发电机额定容量和惯性时间常数Tab.1 Rated capacity and inertia time constant of generators in the wind-thermal bundled system

3.1 风火配比优化分析

对无风机接入时的系统进行小干扰稳定分析，得到系统主要振荡模态如表2所示。

表2 风火打捆系统振荡模式Tab.2 Oscillation modes of wind-thermal bundled system

小干扰分析结果表明，该系统有两个本地模式和一个区间模式，本文着重对区间模式进行分析。由表2可知，区间模式阻尼比仅为3.74%，不满足系统小干扰稳定要求（阻尼比大于5%），需对系统进行调度，减小联络线传输功率，将区间模式阻尼比提升到5%以上，调度前后区间振荡模态的频率和阻尼比如表3所示。

表3 调整联络线功率前后风火打捆系统区域间振荡模式Tab.3 Inter-area oscillation modes of wind-thermal bundled system before and after adjusting tie line power

将联络线功率从419 MW降低到223 MW后，区间模态阻尼比从3.74%提高到5.05%，满足了小干扰稳定性要求，但却降低了风火打捆外送功率。

利用本文所提的优化模型对风火配比进行优化计算。通过改变发电厂G2中火电机组的启停状态并用等容量的风电机组并网代替停机的火电机组以改变风火配比。将临界阻尼设置为5%，通过滑窗分析获得200个风火打捆送端系统等效惯量HASG1的优化结果，如图5所示。

图5 200次优化计算结果分布Fig.5 Distribution of optimization results for 200 calculations

从图5（a）中可以看出，优化结果在其平均值附近波动，与平均值偏差不大。此外其频数分布图5（b）中的概率分布拟合曲线在平均值处也有明显峰值。

根据优化结果的平均值HASG1=88.95s以及式（17）和（18），可以得到此时发电厂G2内同步机剩余开机数为5台，此时区域1内风电和火电输出容量配比为350：1 050 MW。保证总送出功率不变选取以下4种风火配比进行对比分析：0：1 400 MW、280：1 120 MW、350：1 050 MW、420：980 MW。对以上4种不同风火配比进行低频振荡模态分析，结果如表4所示。

表4 不同风火配比下区域间振荡模式Tab.4 Inter-area oscillation modes under different windthermal capacity ratios

由表4可知，当风火配比为350：1 050 MW时，区间模式阻尼比为5.09%，满足小干扰稳定性要求，与临界阻尼差异很小，并且保证了风火打捆功率外送能力。表3和表4的模态分析结果表明，在联络线功率变化后，振荡频率变化不超过0.03 Hz；系统等效惯量变化后，频率变化最大差异小于0.005 Hz，其影响可以忽略不计，这也验证了优化模型中假设振荡频率不变的合理性。

3.2 不同风火配比下的时域仿真分析

为了进一步测试风火打捆系统中不同风火配比对系统稳定性的影响，考虑以下两个代表性扰动：

大扰动：在10 s时，在母线7处发生三相短路故障，故障在10.1 s时消除。

小扰动：母线6的负荷有功功率在10 s时增加10%，然后在11 s时恢复到原始值。

不同风火配比下联络线7-9的有功功率的动态响应如图6和图7所示。

图6 联络线有功功率动态响应（情况A）Fig.6 Active power dynamic response of tie line in case A

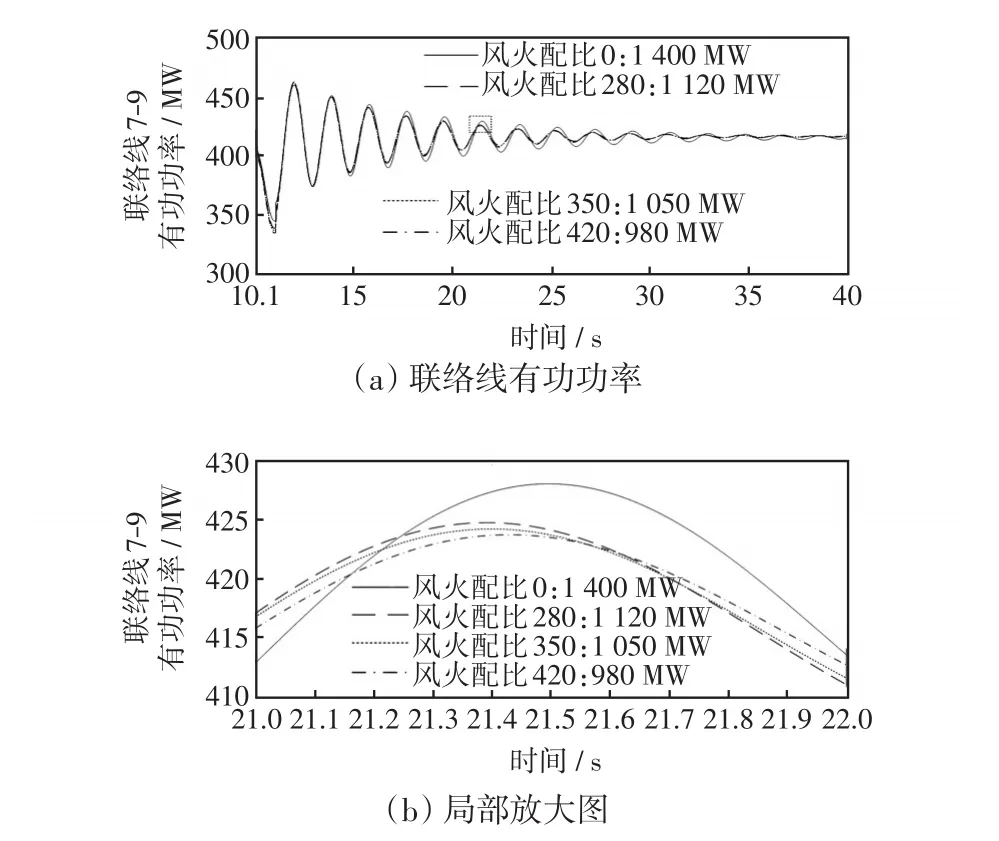
图7 联络线有功功率动态响应（情况B）Fig.7 Active power dynamic response of tie line in case B

通过图6和图7的对比可以发现，系统中不含风电时传输线的功率振荡幅度大于风电接入后的功率振荡幅度。对风火配比进行优化后，功率振荡衰减速度更快，瞬态振荡幅度更小，改善了系统扰动后联络线功率振荡的情况，从而进一步说明选取合适的风火配比能够改善系统的稳定性。

4 结论

研究风火配比对风火打捆系统小干扰稳定性的影响具有重要意义。本文研究了风火打捆系统小干扰稳定性分析方法。提出了考虑小干扰稳定约束的风火配比优化模型。通过仿真算例验证了本文所提方法的有效性和准确性，结果表明：

（1）利用两机等效系统构建的风火打捆系统小干扰稳定分析模型能够准确反映区间振荡模式阻尼比与区间传输功率和系统等效惯量的关系；

（2）对于风火打捆系统，风火打捆外送功率和系统等效惯量是影响系统小干扰稳定性的关键因素。选取合适的风火配比能够改善系统小干扰稳定性并保证风火打捆功率外送能力。