基于地震属性集成学习的自然伽马测井数据预测方法

单立群,祁妍嫣,姜淑贤,刘彦昌,刘修远

(1.东北石油大学秦皇岛校区,河北秦皇岛066004;2.西南石油大学石油与天然气工程学院,四川成都610500;3.大港油田公司同欣集团综合管理部,天津300280)

0 引 言

准确、高效地进行油藏描述是油气藏工程中最常见、最具挑战性的工作。地震数据提供了有关地质井间非均质性的宝贵信息,减少了盆地和油藏地质建模的不确定性。地球物理测井中的地震反演是油气藏定性过程中的一个重要步骤。它可以将地震反射数据转换成储层的定量岩石性质描述[1],这些性质与孔隙度、渗透率、岩相、流体饱和度等岩石物理特征有关[2]。测井曲线通常用于油藏描述,作为条件约束或反演结果的验证,可以直接测量井位的岩石和流体性质,给出岩石的弹性和物理性质[3]。Doyen[4]首次提出了利用地震属性预测储层属性的想法,利用地质统计学方法从水平的单地震属性中获得储层属性。该方法在20世纪90年代初被推广到使用多个属性,提出了在井位建立地震属性与储层属性统计关系的多属性方法。Schultz等[5]利用这种关系预测储层参数。Kalkomey[6]发现在反演过程中涉及太多的属性会导致孔隙度预测的测井曲线高度不准确。

目前,储层参数预测主要使用人工神经网络(Artificial Neural Network,ANN)、支持向量机(Support Vector Machire,SVM)、模糊逻辑方法、模拟退火法、粒子群优化和遗传算法等[7-11]。这些技术使用多属性地震数据,所获得的储层特征与井眼内存在的固有不确定性无关,提高了油气行业储层物性预测的准确性。但是,上述技术训练单个模型以寻求对训练数据模式的理解。单一模型往往会过度拟合,导致预测效果不佳。同时,这些方法没有考虑地震属性的重要性对测井曲线识别精度的影响。针对这些问题,提出基于集成学习的自然伽马测井曲线预测方法,与传统方法比较,该方法具有较高的预测精度。

1 理论方法

1.1 集成学习

集成学习在处理小样本、高维度、复杂的数据结构方面具有独特的优势,是机器学习和模式识别领域的研究热点。集成学习方法通常是将多个机器学习模型(如决策树、人工神经网络、朴素贝叶斯等)的预测结果结合起来,形成集成学习模型,以提高预测的准确性和泛化能力。与在单个模型上进行参数调整的传统做法相比,聚合来自多个模型的结果是提高模型精度的一种更复杂的方法。由于决策树对训练集上的微小变化非常敏感,适合于训练数据的摄动过程,所以集成学习方法一般都使用决策树作为基类学习器。以协商一致的方式组合基类学习器,通常使用投票或平均的组合策略。

1.2 随机森林

随机森林(Random Forest,RF)是一种基于树的集合方法,利用bagging方式生成整个训练集的各种子集来构建单独的树。RF基类学习器通常选择分类和回归树算法,在每个节点的分割过程中,随机选择1个特征子集,而不是考虑所有可用的特征。在结构树中,独立向量和随机向量是同分布的,禁止在RF中修剪树木。这样,在给定相同的训练样本的情况下,生成的树是随机构建的,并且主要由生成的随机向量控制。RF可能会产生不同的树,从而在树之间提供额外的多样性。由于采用了树的组合算法,使得预测精度有了明显的提高。

1.3 AdaBoost算法

AdaBoost算法的主要思想是针对同1个训练集训练不同的分类器(弱分类器),然后把这些弱分类器集合起来,构成1个更强的最终分类器(强分类器)。Adaboost算法本身是通过改变数据分布实现的,它根据每次训练集之中每个样本的分类是否正确,以及上次的总体分类的准确率,在随后的训练中,尽量少考虑那些容易识别的样本,而前几轮中被错误分类的例子将引起更多的注意,来确定每个样本的权值。将修改过权值的新数据集送给下层分类器进行训练,将每次得到的分类器融合起来,作为最后的决策分类器。

1.4 XGBoost算法

XGBoost算法是1种梯度提升集成树的构建方法,通过不断地添加树,不断地进行特征分裂来生长1棵树,每次添加1个树,其实是学习1个新函数f(x),拟合上次预测的残差。当训练完成得到k棵树,得到预测1个样本的分数,然后根据这个样本的特征,在每棵树中落到对应的1个叶子节点,每个叶子节点就对应1个分数。最后只需要将每棵树对应的分数加起来就是该样本的预测值。

XGBoost算法使用了一阶和二阶偏导,二阶导数有利于梯度下降地更快更准。使用泰勒展开取得函数做自变量的二阶导数形式具有足够的灵活性,仅仅依靠输入数据的值就可以进行叶子分裂优化计算,这将损失函数的选取和模型算法优化(参数选择)分开,这种去耦合增加了XGBoost算法的适用性,使得它按需选取损失函数,可以用于分类,也可以用于回归。

1.5 自然伽马测井曲线预测的基本步骤

①收集特征测井曲线和地震资料;②从研究区地震体中提取地震属性;③将测井和地震属性整合到同一个域中;④对测井和地震属性进行预处理和归一化;⑤通过XGBoost算法分析,优选地震属性中重要的特征来预测各类测井曲线;⑥利用网格搜索和交叉验证优化集成学习(XGBoost、AdaBoost和随机森林)方法的参数;⑦利用所选特征和最优参数训练集成学习模型,构建测井曲线预测模型;⑧利用建立的集成学习模型对地震资料进行测井预测和评价。

2 样本集构建

2.1 数据收集

在大港油田X区块A区明化镇组高产砂岩储层收集了125口井的常规测井资料,包括补偿中子测井、自然伽马测井、自然电位测井、声波测井、中子伽马测井、微梯度电阻率测井、0.5 m电位电阻率和2.5 m梯度电阻率测井资料。研究区测井自下而上进行,深度间隔为0.125 m,测井数据是十进制格式。搜集的三维叠后地震数据总面积约为6.5 km2,测量时间间隔是2 ms,在整个时间范围内数据质量良好。在该研究中,从地震数据中提取的属性是测井预测的输入数据;输出数据是由地震属性估计得到的测井数据。选择岩石物理研究中最常用的34个地震属性作为测井数据预测学习模型的候选输入(见表1)。

表1 地震属性列表

2.2 测井数据预处理

通过对测井资料分析,首先选取研究区中的5口井进行测井曲线深度校正。然后,对测井数据进一步处理,包括数据清洗、数据归一化和数据标准化。

关于数据清洗,本研究采用均值替代方法和散点图可视化方法剔除异常值和噪声信息。

数据归一化能够减少不同测量设备在不同时间观测到的测井数据系统误差,可以使所有测井数据符合相同的标准。同时,数据标准化具有加快训练过程的作用。在本文的实验中,根据式(1)将输入序列被缩放到0到1的范围实现归一化。

(1)

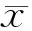
测井曲线标准化步骤:①确定全区稳定分布的标准层(选择厚段泥质层);②采用直方图进行特征峰值的分析和确定标准井;③将待标准化的井峰值以标准井为基准,进行标准化处理。

2.3 测井数据和地震数据集成

由于测井资料(深度域)和地震资料(时间域)在不同的尺度域有不同的分辨率,测井资料和地震资料需要整合到同1个尺度域。首先,测井数据从深度转换到时间域,以匹配地震剖面;然后将地震响应与测井数据在准确的井位进行匹配。本文利用Jason Geoscience Workbench(JGW)软件确定井震时间深度关系,每隔2 ms从井筒轨迹中提取1个测井数据点,实现测井数据与地震数据具有相同的尺度。

2.4 地震属性优选

使用XGBoost算法进行地震属性重要性分析,优选重要的属性进行测井曲线分析,地震属性重要性由XGBoost算法获得的权重值来评价。以自然伽马预测为例,图1显示了34个地震属性在预测自然伽马曲线时的重要性权重。在直方图中,属性1排名最高,而属性9、17、22、23、26、27和29与自然伽马没有相关性。重要性属性选择基于得分为0.01或更高的权重。

图1 预测自然伽马时地震属性重要性权重

2.5 样本集构建

测井曲线预处理和地震属性优选后,构建样本数据集。根据测井样本个数确定地震数据点,以保证模型输入与输出的一致性。确定该研究区用于自然伽马预测的数据集样本个数为1 111,声波测井预测的样本个数为2 121,自然电位测井预测的样本个数为2 121以及微梯度电阻率测井预测的样本个数为1 919。数据集被随机分为训练集(80%)和测试集(20%)。利用训练集学习输入地震属性与测井曲线之间的关系,保留测试集以评估最终学习模型的效率。用于模型测试的数据没有用于训练和最终优化的训练过程,仅用于最终的模型性能分析。

3 实验结果与讨论

3.1 预测准确性评价

该研究所有成果均由Python软件平台实现,采用网格搜索与十折交叉验证相结合的方法对模型参数进行优化,采用均方根误差(MSE)和决定系数(R2)评价集成学习模型预测准确性。

图2～图4为测试阶段预测的测井曲线与实际测井曲线的对比。测试阶段对应的预测数据点几乎落在真实测量值附近,集成学习模型的预测结果与实际测井数据吻合较好,表明提出的集成学习模型在地震资料与测井资料的匹配方面具有良好的性能。因此,本文提出的集成学习方法能够较好地预测非均质砂岩油藏生产过程中缺失的自然伽马测井曲线。

图2 XGBoost算法预测与实际自然伽马测井对比

图3 AdaBoost算法预测与实际自然伽马测井对比

图4 RF算法预测与实际自然伽马测井对比

表2为在地震属性重要性选择阈值下,利用不同的集成学习模型预测自然伽马测井曲线时,在测试阶段得到的均方根误差和决定系数。由表2可见,通过优化地震属性选择,XGBoost、AdaBoost和RF集成学习算法对非均质砂岩储层测井曲线具有较好的预测效果。3种方法预测测井曲线得到的均方根误差值均小于0.009,决定系数R2值均大于0.950 0。从表2中可以看出,当阈值为0.05时,预测精度较高。

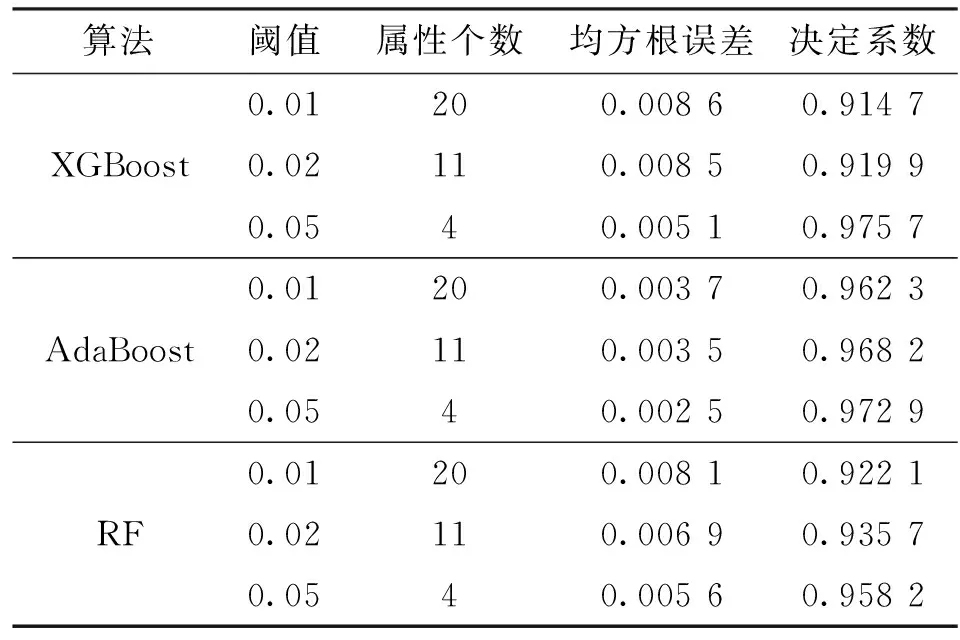
表2 集成学习算法评价参数

3.2 模型对比评价

图5描述了XGBoost、AdaBoost、RF、ANN和SVR这5种算法预测自然伽马时预测数据点和实际数据点的分布,其中特征重要性阈值设置为0.05。XGBoost、AdaBoost和RF算法预测的自然伽马数据点与实际自然伽马数据点接近,具有显著的一致性。基于ANN和SVR算法预测的自然伽马测井数据点与实际的自然伽马测井数据点离散,数据一致性较差,这表明集成模型比用ANN和SVR算法预测自然伽马更准确。

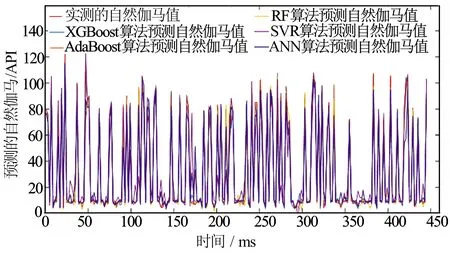
图5 集成学习算法与ANN、SVR算法对比

4 结 论

(1)将测井曲线和地震体的异构数据进行集成,实现基于集成学习方法的测井曲线预测。

(2)新开发的自然伽马预测算法生成的决定系数值大于0.950 0,均方根误差值小于0.009。这些数值表明该研究采用的方法对项目研究的非均质砂岩储层测井曲线具有良好的预测效果。

(3)将已有的研究结果与集成学习算法进行了比较,结果表明集成学习算法在预测测井曲线方面具有更好的性能。