层状边坡的地震动输入方法研究

毕仲辉， 张燎军， 翟亚飞， 唐彧杰， 张汉云

(河海大学 水利水电学院， 江苏 南京 210098)

1 研究背景

我国西部地区因其独特的地质构造和地质环境，常发生地震灾害[1-2]。其中，地震引发山体滑坡是最常见的地质灾害之一，其具有分布广、数量多、破坏性大的特点[3]。一批大型水利工程已经在西部建成，库区边坡中有一部分是层状边坡，在地震作用下边坡更容易发生失稳破坏。因此，分析层状边坡的动力变形破坏机制和研究边坡的动力响应规律十分必要。

已有大量的学者通过振动台模型试验和数值模拟方法对边坡的动力响应规律进行了研究。刘新荣等[4]基于振动台试验研究了在往复地震作用下边坡的累计损伤对层状岩质边坡稳定性的影响；黄润秋等[5]通过大型振动台试验，研究了反倾向和顺层向两类结构在强震作用下的地震动力响应；刘汉东等[6]开展了地震波频率对反倾向层状岩质边坡影响的试验研究；刘汉香等[7]进行了层状复合岩体边坡动力特性和动力响应研究的振动台试验。与振动台试验相比，数值模拟方法因成本低和操作方便等优点被广大研究人员采用。刘云鹏等[8]采用离散元的方法研究了地震作用下反倾软硬互层岩体边坡的动力响应；言志信等[9]基于FLAC3D研究了基岩型层状边坡在地震作用下的响应规律和变形机制；周剑等[3]基于应力波传播原理分析了层状边坡在地震作用下的损伤机理和破坏模式；周英博等[10]基于4种不同岩质边坡，开展了不同地形地质的地震动传播特性研究。

上述数值模拟方法中动力边界均采用黏性边界，而黏性边界不能真实地模拟地震波的辐射阻尼效应。事实上，在众多的人工边界条件中，黏弹性人工边界可以同时模拟散射波的吸收和边坡边界的弹性恢复能力，因此得到广泛应用。张伯艳等[11]基于黏弹性人工边界研究了白鹤滩水电站岩石边坡的动力稳定性；尹超等[12]在边坡的截断边界上采用黏弹性人工边界，研究中考虑了拉剪耦合作用下地震边坡的稳定性；张江伟等[13]采用黏弹性人工边界模拟了不同地震动参数对边坡动力响应的影响。上述研究在采用黏弹性人工边界模拟边坡的辐射阻尼效应时，均以均质边坡进行模拟，而天然状态下的边坡往往都是呈层状非均质分布。

本文在前人研究成果的基础上，结合波动理论，构建了一种水平层状边坡的地震动输入方法。该方法不仅考虑了散射波的吸收和边坡截断边界的弹性恢复能力，还考虑了弹性波在不同介质中的透射和反射特点。通过对ABAQUS的二次开发来实现层状边坡的地震动输入，以此分析地震作用下层状边坡的动力稳定性。

2 层状地基的人工边界

用数值方法模拟结构和地基的相互作用时，考虑到天然地基为半无限域，数值模拟计算量很大，需从天然地基中截取有限的近域地基进行计算，并在近域地基的边界上施加人工边界，模拟无限地基对地震波的辐射阻尼效应[14-15]。

图1为近域层状地基模型示意图，该模型共有f层，地震波由模型底部垂直入射，近域边界施加人工边界。

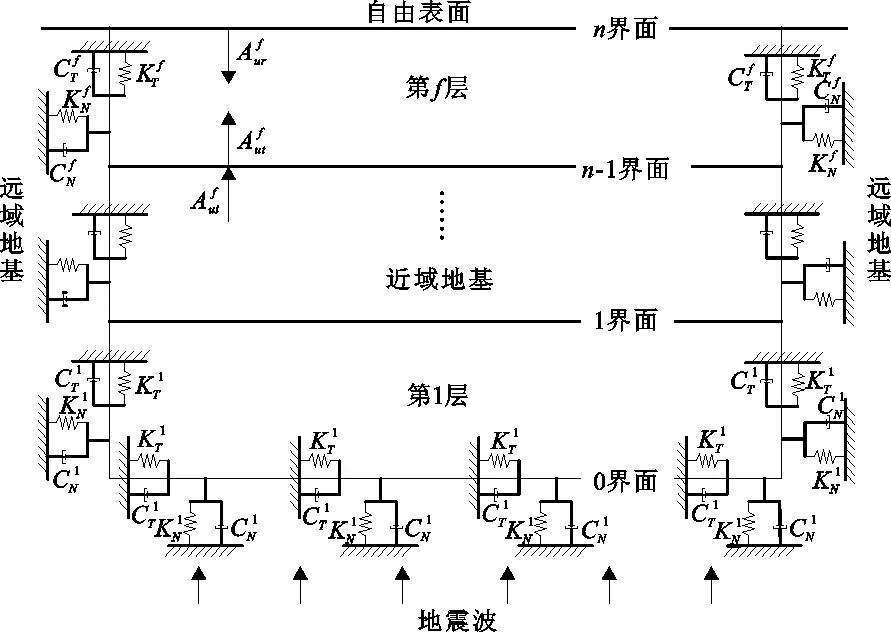
图1 地震波入射近域层状地基模型示意图

黏弹性人工边界可以用空间连续分布的并联弹簧-阻尼器元件模拟。二维黏弹性人工边界上施加的弹簧和阻尼器参数为[16]：

(1)

(2)

(3)

(4)

其中：

(5)

(6)

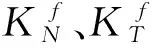
本文运用有限元程序中弹簧-阻尼单元实现层状地基的黏弹性人工边界，弹簧单元的刚度系数及阻尼器单元系数可根据公式(1)～(4)取为：

(7)

(8)

(9)

(10)

二维有限元模型弹簧阻尼单元如图2所示。

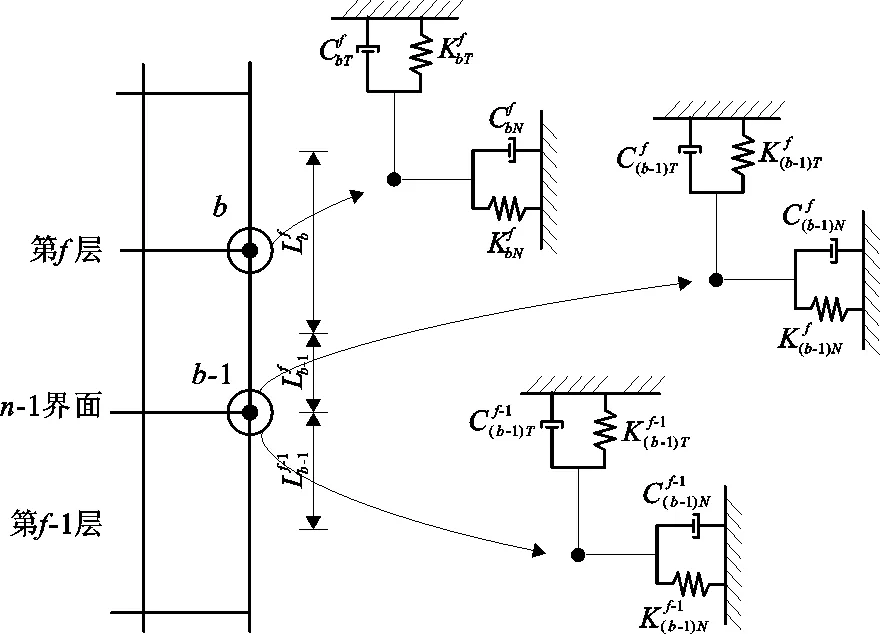
图2 二维有限元模型弹簧阻尼单元示意图

3 层状地基的地震动输入方法

3.1 地震波入射时反射波和透射波的波幅比

地震波从一种介质进入另一种介质时，会在两种介质的分界面上发生透射和反射，反射波会在入射的介质中向下层传播，而透射波会在上层的介质中向上传播[17]。P波和S波垂直射入不同介质分界面时，其产生的反射波和折射波的波型不发生变化，如图3所示，其中黑色箭头表示波的传播方向，灰色箭头表示波的振动方向。

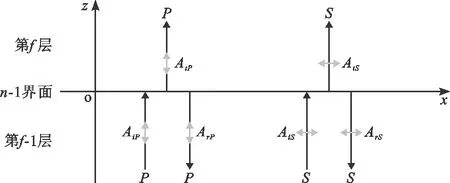
图3 P波和S波的入射、反射和折射示意图

假定第f层与第f-1层介质的剪切波和压缩波的波阻抗之比分别为zsf和zpf，其计算公式如下：

(11)

(12)

当地震波从第f-1层垂直入射至第f层时，第n-1界面的反射波、透射波与入射波的波幅比计算公式如下：

(13)

(14)

(15)

(16)

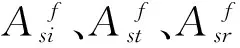
3.2 等效节点荷载推导

地震作用下，成层地基复杂波场中共包含入射波、反射波、透射波和散射波4种波场，其中入射波、反射波和透射波为自由波场，散射波场由人工边界来吸收。作用在截断边界上的等效节点力由两部分组成，一是克服人工边界单元刚度和阻尼所需要的力，二是自由波场在人工边界处的应力场，其计算公式为[18]：

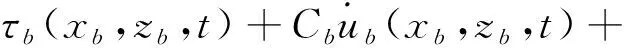
Kbub(xb,zb,t)

(17)

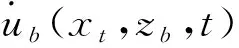
在地震波垂直入射的情况下，介质交界面不会产生波型转换，但是由于波的反射和折射作用，各个波会发生叠加。对于边界节点等效荷载的计算，可根据公式(13)～(16)，求得不同的介质之间的波幅比，从而确定相应的波幅变化系数。由波动理论和单元应变状态，代入公式(17)中得到各个边界的等效节点力，计算公式如下：

(18)

(19)

(20)

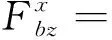
(21)

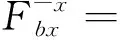
(22)

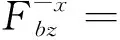
(23)

当f>1时，有：

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

(35)

当f=1时，有：

(36)

(37)

(38)

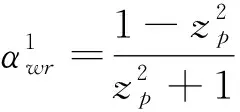
(39)

(40)

(41)

(42)

(43)

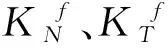
4 算例验证

4.1 双层水平地基模型

对ABAQUS进行二次开发，编写相应层状地基的地震动输入程序，与解析解进行对比，从而验证本文提出的反透射黏弹性人工边界的合理性。计算模型如图3所示，模型为两层地基模型，坐标原点位于地基底部的中点。地基上下两层的密度均为2 000 kg/m3，泊松比为0.25，上层地基的弹性模量为2 GPa，下层为10 GPa。

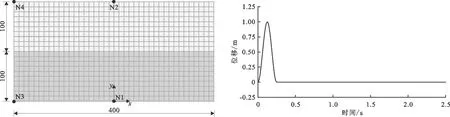
图3 两层层状地基计算模型(单位：m) 图4 验证计算输入的位移时程曲线

为了比较波动输入方法的准确性，采用地基顶部解析解的值作为参考解，并设置2种不同地震动的输入方法：方法1假定弹性波不在介质分界面产生反射作用，仅在地基顶部发生反射；方法2考虑弹性波在不同介质分界面的反射作用。假设从模型底部垂直输入单一周期的剪切波，输入的位移时程曲线如图4所示。

4.2 计算结果与分析

图5为两种不同地震动输入方法及解析解在观测点N3和N4的位移时程曲线。分析图5(a)可知，在第1个周期内，方法1的位移幅值小于方法2和解析解的位移幅值；分析图5(b)可知，在第1个周期，方法1和2的位移幅值均等于输入值1 m，方法1的传播规律与方法2和解析解相比均有较大差异。总体来看，在层状地基中考虑波在介质分界面的一次反射作用，与解析解的值更加接近，能较好地模拟波在层状地基中的传播特性。

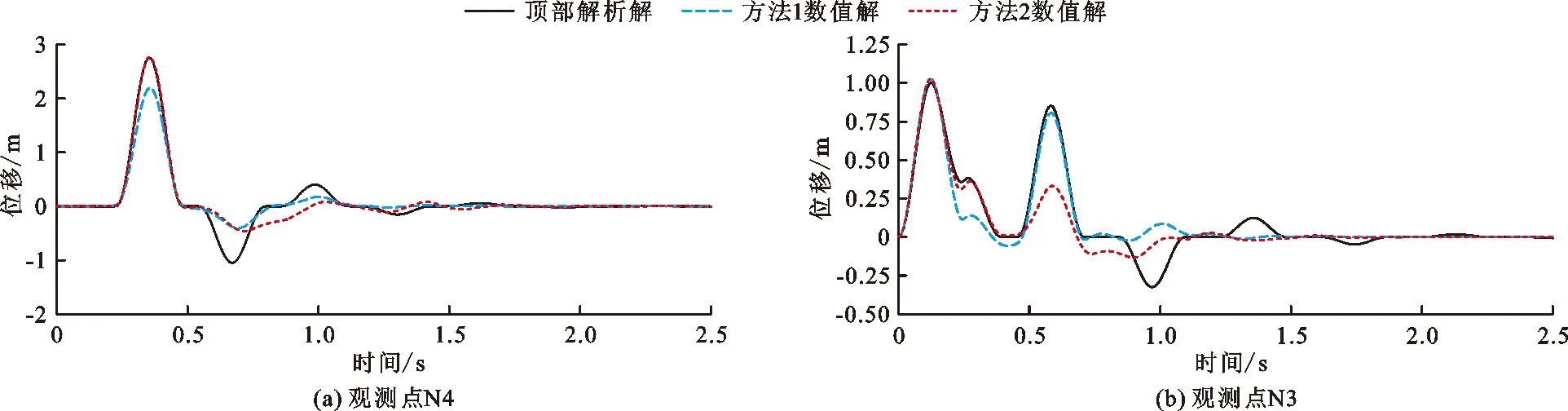
图5 两种不同地震动输入方法计算的N3、N4观测点水平位移

通过公式(13)～(16)计算可得，SV波从第1层传递到第2层的波幅放大系数为1.38，输入SV波的位移幅值为1 m，故地基顶部的最大位移理论值为2.76 m。图6为采用方法2计算的各观测点水平位移，由图6(a)可知，顶部观测点N2和N4的最大位移幅值计算值为2.78 m，与最大位移理论值比较接近，且在第1个周期内，波的传播规律和位移响应基本一致，具有较高的稳定性；由图6(b)可知，底部观测点N1和N3的最大位移幅值计算值为1.00 m，与输入位移幅值误差较小，且在传播的规律上，第1个周期前面部分基本相同，位移响应也基本一致。

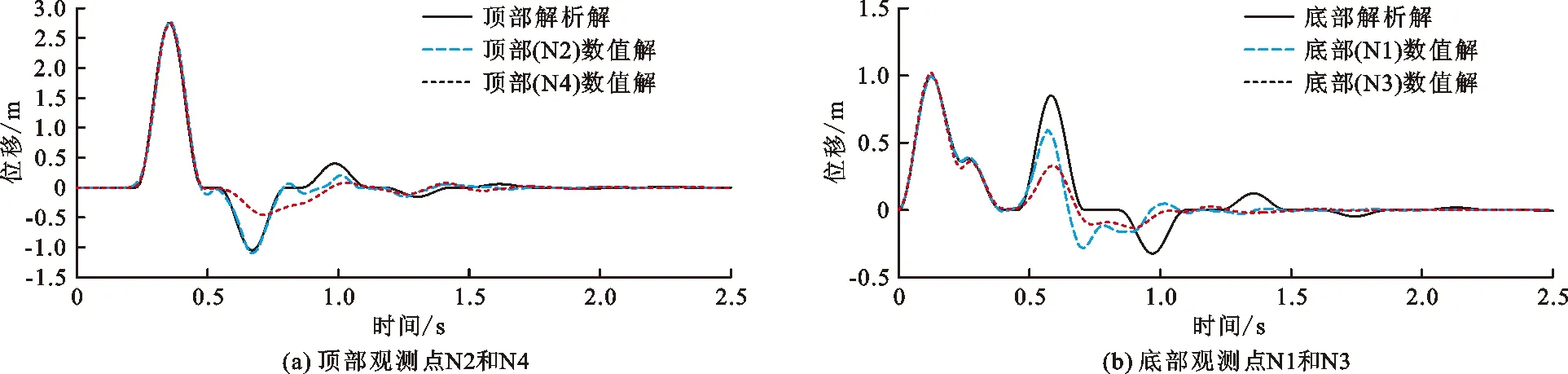
图6 采用方法2计算的各观测点水平位移

5 层状边坡动力稳定性实例分析

5.1 实例工程概况与有限元模型

选取我国西部地区某实例工程层状边坡作为研究对象，建立的有限元模型如图7所示。该工程边坡坡高为30.0 m，坡角为60°，共分为3层(Ⅰ～Ⅲ层)，从下到上依次为硬岩(Ⅰ层)、软岩(Ⅱ层)和碎石土(Ⅲ层)，各层的材料属性如表1所示。3种材料分析选用MC本构关系模拟非线性，分别在边坡的截断边界施加层状黏弹性人工边界。采用两种不同的波动输入方法，方法1为假定弹性波不在介质分界面产生反射作用，仅在地基顶部发生反射；方法2为考虑弹性波在不同介质分界面的反射作用。

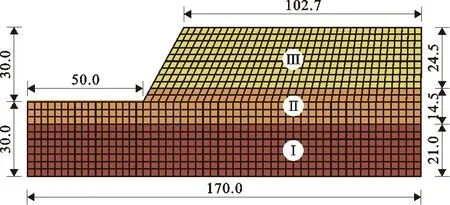
图7 实例工程层状边坡有限元模型(单位：m)

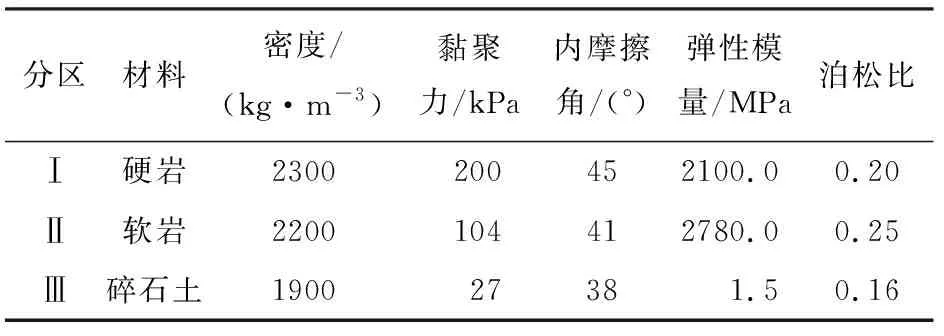
表1 实例工程边坡的材料参数

边坡模型采用ABAQUS中的CPE4单元模拟，整个模型共有947个单元和1 023个节点。本文考虑的荷载为自重和地震作用。通过反应谱合成时-频非平稳人工地震波，地震历时为20 s，水平加速度峰值为0.200g，竖直加速度峰值为0.133g，水平向和竖直向地震波加速度时程曲线如图8所示。通过公式(13)～(16)计算可得，剪切波和压缩波从边坡底部传播到坡顶表面放大的倍数分别为3.72和3.61倍，故剪切波和压缩波输入加速度时需要分别缩小3.72和3.61倍。

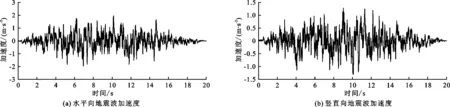
图8 实例计算加载的地震波加速度时程曲线

5.2 边坡塑性应变能

在地震的作用下，边坡通过调整应力和应变的发展趋势来维持稳定，当荷载破坏性超过边坡自身调节能力时，边坡便会发生失稳破坏[19]。边坡的塑性应变云图如图9所示，两种方法计算的总塑性应变能时程曲线如图10所示。

由图9可以看出，两种地震动输入方法下边坡的上层碎石土塑性区扩展规律相似，均产生了从碎石土层坡脚向坡顶延伸的弧形滑裂带；从数值上来看，考虑波反射和透射过程(方法2)时比未考虑时(方法1)的塑性应变要大。由图10可以看出，0～1 s为静力作用，总塑性应变能呈直线上升；1～5 s塑性应变能增加缓慢，在0～5 s之间，两种不同输入方法的总塑性应变能变化基本相同；6～21 s总塑性应变能增幅比较明显，且考虑波的反射和透射作用时的总塑性应变能比未考虑时的大。

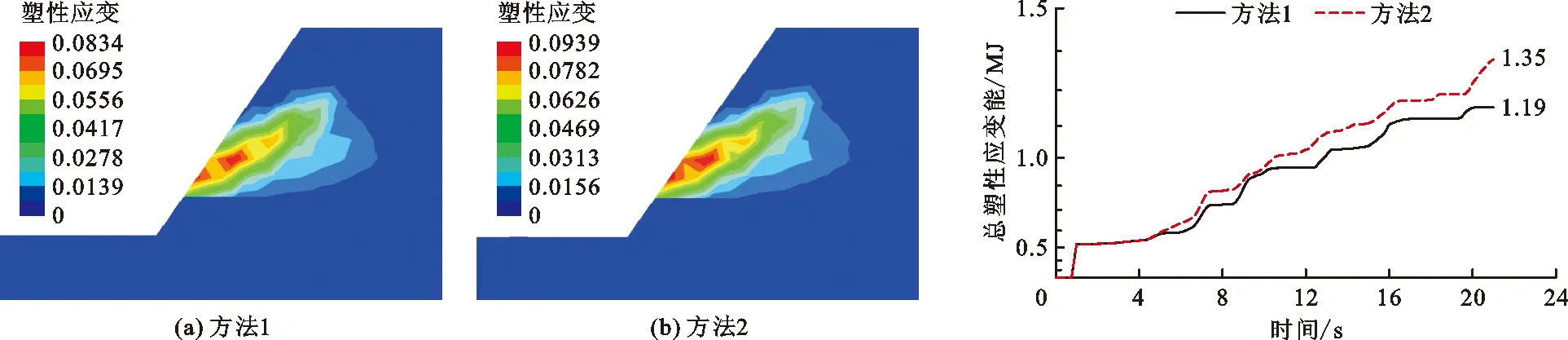
图9 实例计算边坡塑性应变云图 图10 两种方法总塑性应变能时程曲线

5.3 边坡动力安全系数

在地震作用下，对边坡上层碎石土层的稳定性分析采用强度折减法[20]，从而获得多级动力折减系数下的总塑性应变能，并且据此绘制动力折减系数与总塑性应变能的关系曲线，如图11所示。本文构建了地震后边坡的总塑性应变能与动力折减系数的尖点突变模型[21]，基于尖点突变理论的判据，客观地确定边坡的动力安全系数。

由图11可以看出，边坡的总塑性应变能随着动力折减系数的增加而增加，说明边坡在较低的抗剪强度下，塑性应变更大；在相同的动力折减系数下，方法2的总塑性应变能略大于方法1，且主要体现在动力折减系数为1.0～1.1之间。

图11 两种方法总塑性应变能与动力折减系数关系曲线

根据建立的尖点突变模型，方法1和方法2的边坡动力安全系数分别为1.083和1.078；通过对比不难发现，采用地震动输入方法2时，边坡更加易于失稳，因此在针对层状边坡的动力稳定性分析时，应该考虑地震波入射不同介质分界面时的反射和透射作用。

6 结 论

本文首先针对层状地基模型，提出了考虑地震波在介质交界面的一次反射的波动输入方法，并通过两层水平地基模型验证了该方法的正确性。然后将层状地基地震动输入方法运用到层状边坡的动力稳定性分析中，分析比较两种不同输入方法下边坡的动力响应规律，得出以下结论：

(1)在地震波的波动输入方法上，本文提出的方法更加接近理论解，满足工程精度要求。

(2)采用本文提出的地震动输入方法计算时，层状边坡会产生更大的塑性应变，且动力安全系数更小。

综上所述，本文针对半无限层状地基提出的波动输入方法具有较高的精度，且适用于层状边坡的动力稳定性分析。