降雨条件下大孔隙土体含水率变化规律研究

樊秀峰， 严佳捷， 吕 捷， 吴振祥

(1.福州大学 环境与资源学院， 福建 福州 350108; 2.地质工程福建省高校工程研究中心， 福建 福州 350108)

1 研究背景

降雨条件下优势流的运移对边坡稳定性的影响很大[1-2]，优势流对边坡的影响与孔隙发育程度之间存在着密切的联系[3-4]。强降雨条件下的水流沿着由动物活动、植被根系生长等造成的随机分布的孔隙通道快速下渗，表现出优势渗流的非均匀性，其中土体不同深度含水率的时空演化规律各异[5-6]，但目前降雨入渗补给土体的研究主要以均质性渗流为主[7-9]，其分析结果与实际存在优势通道的边坡的渗流状态差异较大，说明均匀性渗流理论不适用于部分优势流特征明显的边坡渗流[3]，所以开展边坡降雨入渗优势流研究极为必要。

目前优势流相关问题在土壤学中研究较多，主要集中于优势流形成机理与模型理论方面[10]，其追踪土体内部渗流路径分布特征与水流的优先运移规律的方法主要通过室内土柱实验、染色示踪法[11-12]、数值模拟[13]等实现，如张家明等[14]、吴庆华等[15]、盛丰等[16]通过染色示踪试验跟踪分析了大孔隙非均匀优先流路径，针对优先流类型、发育程度及其影响因素等方面展开了研究；阙云等[17]、苏立君等[18]基于优势流传统模型理论(两域模型)结合运动波模型、分形理论，围绕不均匀入渗规律与水分非均匀迁移特性等内容进行了研究。优势流通道[19]形成机理复杂且涉及影响因素多，其土体含水率对优势流发育有着一定程度的影响，但对于大孔隙等通道引发优势渗流含水率变化方面的研究很有限，所以需要深入研究优势通道含水率的空间响应规律。

因此，本文拟借助一维土柱降雨入渗试验以及染色示踪法评估原状土优势通道发育程度，由试验动态监测结果分析对应孔隙类型土体的优势渗流含水率变化规律，通过数值模拟深入分析孔隙土体模型参数对含水率分布的影响。

2 室内土柱降雨入渗试验

2.1 试验土样

本次试验选择福州大学生活区残积土边坡的露头坡体发育大孔隙的原状土样，通过室内土工试验测得试验土样的相关参数见表1， 于相同地点选取扰动土并按照原状土柱天然密度(ρ=1.924 g/cm3)进行重塑，分层击实保证重塑土柱和原状土柱具有相同的密实度，基本指标如初始含水率、天然密度与原状土一致。

表1 边坡残积土试样参数

2.2 试验方案

为评估土柱大孔隙发育特征，通过室内土柱染色渗流试验获得如图1所示的大孔隙发育形态各异的原状土柱竖直剖面，图1中虚线线段为染色剂显示的孔隙位置与大小。由图1(a)可看出原状土大孔隙由浅至深贯通至土样底部，通道狭长且分支少，大孔隙整体呈竖直贯通状；由图1(b)可看出原状土通道孔隙大且分支多，但未贯通至土样底部，出现死端孔隙；由图1(c)可看出原状土孔隙通道小且多，各向分布于土柱内部，所以根据原状土柱剖面分布各异的孔隙特征将各类原状土柱试样命名为竖直贯通样、死端孔隙样、各向展布样。

图1 土中不同形式典型大孔隙发育类型图

试验是通过染色示踪法获得的土柱剖面的孔隙分布，由局部剖面二维特征以及含水率变化反映整体情况。采用CT可以给出土柱孔隙三维分布图并可针对细节作出描述用于深入的新课题研究，但本次研究针对含不同大孔隙的土体含水率变化规律而展开，采用室内染色示踪试验以及含水率测定方法可以获得满意的试验结果，因而并未另外考虑CT试验。

试验装置主要由降雨系统、入渗试验设备、监控软件3部分构成。试验土柱高30 cm，由上至下按间距10 cm排布土壤水分传感器，各土柱不同深度体积含水率变化均采用防水探头、不锈钢检测探针组合而构成的RS485土壤水分传感器进行测定，适用于多种土质体积含水率的测定。传感器各接口处采用玻璃胶密封，以保证试验过程中无水渗出，土柱下部设置反滤层(填充卵石、碎石)，在其下方放置量杯观测出流量。图2为试验装置示意图。

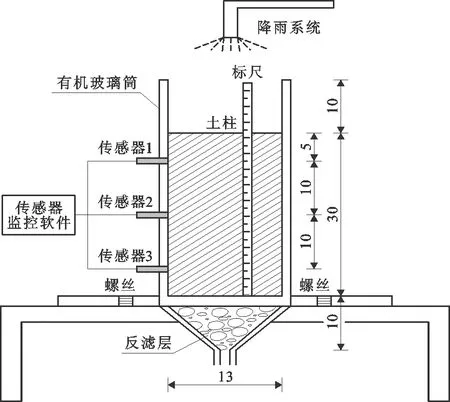
图2 试验装置示意图(单位：cm)

本研究在降雨强度为30 mm/h、总降雨量为30 mm、降雨时间为1 h的工况下进行不同大孔隙原状土柱与重塑土柱的降雨入渗试验。雨水采用亮蓝染色剂溶液，每分钟向土柱表面均匀喷洒染色剂溶液量约为6.6 mL，通过染色示踪法阐明的各土柱优势流路径分布状况如图1所示。

试验动态监测土柱不同位置含水率与底部出流量。前期含水率上升幅度与底部出流量较大时，每隔 5 min 记录一次数据，后期随着含水率增长幅度逐渐减缓，逐步加大记录数据的时间间隔(10、20、30 min)。

2.3 结果分析与讨论

图3和4分别为试验过程中各孔隙特征原状土柱及重塑土柱不同深度含水率随时间变化曲线和底部出流量随时间变化规律。

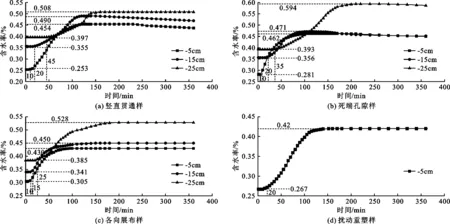
图3 各孔隙特征原状土柱及重塑土柱不同深度含水率时变曲线

由图3可以看出传感器由浅至深依次响应且初始含水率、峰值含水率依次递增，原状土体浅层(-5 cm)传感器响应时间一致(10 min)，由于各向展布样孔隙通道较小，浅层峰值含水率略低于竖直贯通样与死端孔隙样。由图3以及图4可知，重塑试样密实度高，孔隙发育程度很低，水流运移困难，由于深部无明显大孔隙，传感器只在-5 cm处出现响应，水流集中于浅部，底端无出流。降雨过程中，各土体浅层含水率以均匀速率增大至峰值，表现出典型的均匀流入渗模式。

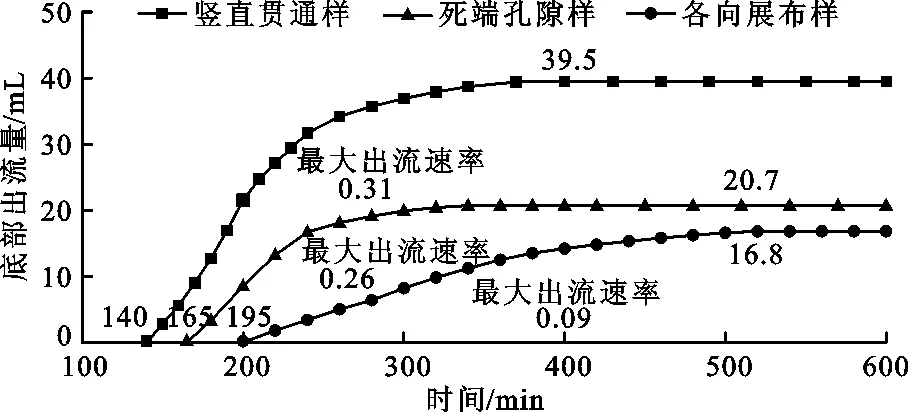
图4 各孔隙特征原状土柱底部出流量随时间变化曲线

各孔隙特征原状土体深部(-15、-25 cm)因优势通道展现出不同的含水率增长模式且水流入渗过程各异，现分析如下：

(1)竖直贯通型样深部密实度高，大孔隙少且单一，含水率以较缓慢速率增长，传感器响应时间最长为45 min，-25 cm处含水率趋近峰值时(125～140 min)出现速率小幅增长的现象。由于孔隙贯通，底端最先发生出流，对应的出流速率与累积出流量最高。另外，由于优势通道窄且狭长，水流通过孔隙优先发生侧渗，大孔隙域与基质域间发生水分交换，导致水流下渗速度慢，响应时间长。在水流运移至深处且含水率较高的状态下，向周围基质区域侧渗的速率降低，汇集至大孔隙的水流下渗速度加快，水流沿贯通孔隙出流后，优势通道及优势流扩散的基质域含水率达到峰值；

(2)死端孔隙型原状土由浅至深存在发育程度较好的大孔隙，深部传感器响应时间为35 min，水流通过优势通道的下渗速度大于竖直贯通型，土体深部(-25 cm)因通道未贯通，导致水流下渗迁移受阻，在死端孔隙部分滞留大量水分，由优势通道向周围扩散造成含水率大幅上升，同时水流通过基质域缓慢下渗至出流，最终达到的峰值含水率高于其他原状土，但由于孔隙未贯通，出流量与出流速率低于竖直贯通样；

(3)各向展布型原状土优势通道多且方向各异，深部传感器响应时间最短，到达-15 cm的响应时间为15 min，-25 cm的响应时间为25 min，土体的含水率上升速率较快。由于各优势通道分散且不连续，后期(100 min之后)水流沿优势通道向周围扩散，出现含水率增速下降的现象，含水率达到峰值一段时间后出流，其峰值略高于竖直贯通型。水流通过整个土柱的出流时间较长，出流量与出流速度较低。

综上所述，大孔隙特征各异的土体表现出浅部水流均匀入渗，深部优势流的水分迁移规律随孔隙特征各异的定性结论，含水率的增长模式在一定程度上可以反映优势渗流的水分运移规律。因此，基于前期试验含水率研究结果，采用数值模拟的方法进一步定量研究土体孔隙特征对含水率分布的影响。

3 优势渗流模型研究

3.1 双重渗透模型理论基础

Richards方程[20]描述了非饱和带水流均匀渗流过程(活塞式渗流)，与土体孔隙分布各异产生优势流的过程不符。学者们针对土体内部优势流运移特征的研究提出了多种理论模型[21-23]。

本文采用的双重渗透模型将土体划分为大孔隙通道构成的快速流动区(优势流)和通道之外的慢速流动区(基质流)，两域水流均符合达西定律并采用Richards方程描述。模型假设水流在大孔隙域、基质域运移，大孔隙域水流运移速度接近完全饱和时远大于基质域。具体模型参数确定采用参数反演优化法实现[24]。双重渗透模型的控制方程：

(1)

(2)

θ=ωfθf+(1-ωf)θm

(3)

式中：θf、θm和θ分别为大孔隙域、基质域及全部区域的含水率，%；hf、hm为大孔隙流和基质流的基质势，cm；Kf和Km为大孔隙域和基质域的饱和渗透系数，cm/min；Γw为大孔隙与基质流区之间的交换水量，min-1；ωf为大孔隙流区与全部流区的体积比；z为垂向坐标轴，向上为正，cm；t为时间，min。

Γw=αw(hf-hm)

(4)

(5)

式中：αw为一阶土壤水传输系数，cm-1·min-1；β为土粒几何形状因子(若土粒为球体取15.0)；γ为经验系数，取值为0.4；a为基质区中心与大孔隙边界的距离，cm；Ka为基质区与大孔隙区界面间的渗透系数，cm/min。

3.2 双重渗透模型模拟结果与分析

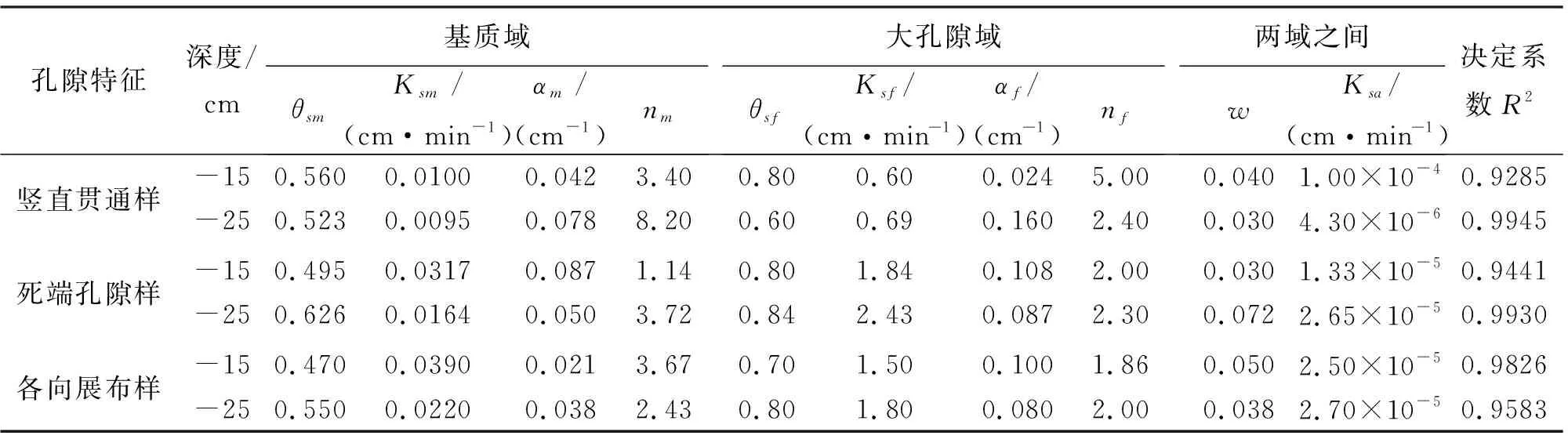
图5为各孔隙特征土柱深部含水率随时间变化的双重渗透模型模拟值与实测值的拟合曲线，表2为双重渗透模型土水特征参数拟合结果。由图5以及表2可知，模型拟合曲线与实测曲线相近且两者的拟合决定系数均达0.9以上，表明该模型能较准确地模拟不同大孔隙类型的土体优势流发育期的水分运移过程。

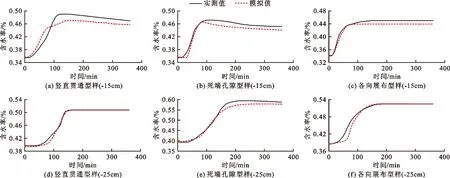
图5 各孔隙特征土柱深部含水率随时间变化的模拟值与实测值拟合曲线表2 双重渗透模型土水特征参数拟合结果

孔隙特征深度/cm基质域θsmKsm/(cm·min-1)αm/(cm-1)nm大孔隙域θsfKsf/(cm·min-1)αf/(cm-1)nf两域之间wKsa/(cm·min-1)决定系数R2竖直贯通样-150.5600.01000.0423.400.800.600.0245.000.0401.00×10-40.9285-250.5230.00950.0788.200.600.690.1602.400.0304.30×10-60.9945死端孔隙样-150.4950.03170.0871.140.801.840.1082.000.0301.33×10-50.9441-250.6260.01640.0503.720.842.430.0872.300.0722.65×10-50.9930各向展布样-150.4700.03900.0213.670.701.500.1001.860.0502.50×10-50.9826-250.5500.02200.0382.430.801.800.0802.000.0382.70×10-50.9583

对表2中3类原状土柱的土水特征参数分析如下：

(1)竖直贯通型样-15 cm处的Ksa(两域交界面处水力传导系数)最高，Ksf(大孔隙域渗透系数)与Ksm(基质域渗透系数)最低，说明水流沿孔隙渗流基质域与孔隙域之间的水分交换强烈且两域的渗透性能不高，表示水流迁移速度慢，与试验响应时长相对应。水流随着通道下渗，Ksa与Ksm降低，Ksf增大，表现出侧渗能力降低，大孔隙域渗流能力增强，水流沿通道向下迁移速度加快，对应后期水流小幅增长的现象。-25 cm处两域含水率θsm、θsf数值低于其余2类样，与试验中的最低峰值含水率相符。

(2)死端孔隙型样w(大孔隙体积与整个土体体积比值)、Ksf、Ksm较大，表明土体大孔隙发育规模大，水流易于由深部大孔隙向下运移且向周围基质域充分入渗，响应较快；两域含水率θsm、θsf最大，与试验含水率的最高含水率峰值相符。水流下渗至死端孔隙(-25 cm)处，Ksa、Ksf增大，Ksm降低，说明水流通过优势通道向周围土体快速渗流，基质域与孔隙域水分交换能力增强，但水流向下渗流速度降低延缓了出流速度与出流量，对应试验中出现的水流因长时间滞留充分向周围基质区域扩散的现象；

(3)各向展布型原状土-15、-25 cm模型参数值相差较小，表明大孔隙于各处分布发育，Ksf、Ksm、Ksa数值较大，说明水流沿优势通道快速渗流且大孔隙域与基质域之间的水分传递能力较强，降雨主要通过大孔隙逐渐扩散至基质土体。

由以上分析可知，双重渗流模型的模型参数能较好地刻画大孔隙的发育特征，适于定量描述不同大孔隙类型的土体水分迁移过程。因此，双重渗流模型拟合在大孔隙土体优势流研究中是有效的。

4 结 论

本文针对降雨条件下不同大孔隙原状土优势流不同位置含水率与底部出流量的变化特征时变规律进行了试验和数值模拟研究，得到结论如下：

(1)浅部土体的水分运移规律相近，表现为典型均匀流入渗模式，含水率均匀增大至峰值；深部土体发生优势渗流的含水率增长模式各异，水分运移规律随孔隙发育程度不同，说明含水率的增长模式在一定程度上可以反映优势渗流的水分运移规律。

(2)土体深部孔隙结构特征不同，优势渗流及含水率增长模式各异。其中，对于狭窄、单一的贯通孔隙通道，水流沿孔隙下渗速度由慢变快与周围土体水分交换由强至弱，水流沿着贯通孔隙快速出流且出流量较大；对于发育较好且无贯通的通道，水流沿优势通道快速下渗，在死端孔隙部分优先侧渗造成含水率较高并导致下渗速度降低延缓出流；对于孔隙发育多且分散的通道，水流沿通道快速运移后向周围土体以较慢的速度扩散导致出流时间较长。

(3)双重渗流模型能较好地拟合土体大孔隙发育特征，参数Ksa、Ksf、Ksm反映水流运移速度的大小与方向，w反映土体孔隙发育程度，两域含水率θsm、θsf反映峰值含水率，所以由模型参数能进一步说明优势流发育期的水分运移过程。希望借助此次不同土体孔隙含水率时变规律的相关研究对强降雨作用下优势渗流特性分析等提供一定的理论依据和实际工程应用价值。