服装制版系统参数量化模式识别

高 旋， 薛 庆

(1.六安职业技术学院 艺术学院，安徽 六安237000; 2.上海大学 计算机工程与科学学院,上海 200444)

在产品的设计、生产过程中，质量控制是至关重要的一个环节[1-3]。本研究针对服装制版系统参数量化模式识别进行设计，并通过仿真实验验证了所提方法的有效性，以期为实际的服装制版系统参数量化模式识别提供一定的理论依据。

1 服装制版系统参数提取及预处理

1.1 服装制版系统参数提取

目前，服装制造行业的质量管理模式以监督、预防为主，要求相关服装制造企业的残次品率为0或接近0[4]。因此，服装制造企业为提升工作效率，必须不断优化服装制版系统。服装制版系统优化实质上是不断优化其制版参数，主要包括长度、颈围、臂围、腰围、胸围、立裆等，本研究首先对这些参数进行提取。

将服装制版系统视为一种三维空间结构[5]，在此结构中获取制版参数坐标的最大值和最小值，分别设为Hmax和Hmin，此时可以获取服装制版的长度参数

C=Hmax-Hmin。

(1)

围度参数是决定服装质量的关键参数，这里以人体腰围为例进行提取。首先确认人体腰高尺寸，即确定腰围的取值范围(图1)。如图1 所示，制版系统中腰围参数曲线如同封闭的椭圆，在该椭圆上存在若干个数据点，这些点共同形成了腰围参数。此时，确定椭圆的周长即可得到腰围参数

图1 确定腰围参数范围Fig.1 Determination of the range of waist circumference parameters

(2)

式中：wi为第i个数据点的距离；n为腰围上的无限个数据点。

根据腰围参数的提取方式，可以通过确定服装制版点间的距离实现围度参数获取：

(3)

式中：a、b、c分别为围度参数封闭椭圆上数据点的坐标。

在上述制版系统参数的提取中，由于服装生产过程中变化因素较多，导致其产品质量控制难度较大，故需要对制版系统参数中易出现的误差概率进行确定。假设连续随机变量X服从正态分布，则对应的概率密度函数

(4)

式中：σ为不同类型的服装材料；e为制图效率。

在实际统计数据为正态分布的情况下，服装制版参数误差出现的错误概率完全不同。为了降低服装制版系统误差出现的概率，设定误差出现的最小概率为α，服装生产过程中不同参数误差出现的概率为P。若P>α，说明服装生产中系统参数无误差；若P≤α，则说明服装生产中制版系统参数存在一定误差[6]，整个生产过程已经处于异常状态。此时，整个生产过程中出现n件服装不合格的概率

s=(1-P)n。

(5)

为了实现服装制版系统参数的模式识别，首先提取服装制版系统中服装的宽度和围度信息，并借助概率密度函数确定服装制版系统参数的误差，然后通过以下方程组计算出参数及驱动集合图形的变化，结合以下方程进行净胸围及背长等相关参数的提取：

(6)

1.2 服装制版系统参数预处理

在上述提取的服装制版系统参数中，由于多种因素影响导致获取的参数维度较高，从而影响服装制版系统的制衣质量，故需要对提取的参数进行降维处理[7]。本研究借助主成分分析法实现了参数的降维处理。

假设服装制版参数中相关性指标为x1，x2，x3，…，xn，将这些参数进行重组，得到服装制版参数

Σ=(ξij)r×r，

(7)

式中：ξij为人体特征部位的尺寸；r为外轮廓线。

式(7)中的人体特征部位尺寸ξij可化为

(8)

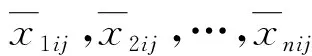
对服装制版系统参数进行重组，其信息贡献率

(9)

式中：εi为服装制版系统参数高维度特征值。

在此基础上，对εi的主成分维数进行降维处理，实现服装制版系统参数的预处理：

(10)

在服装制版系统参数预处理中，借助主成分分析法计算系统参数的信息贡献率及服装制版系统参数高维度特征值，以实现系统参数主成分维数的降维处理，为后续的高精度量化模式识别奠定基础。

2 服装制版系统参数量化模式识别

2.1 服装制版系统参数量化模式识别模型设计

根据上述获取的服装制版系统参数，本研究借助BP 神经网络设计服装制版系统参数量化模式识别模型，使用小波分析方法对该模型求解，获取最优解，以实现服装制版系统参数量化模式识别。

BP神经网络是人工智能领域中较为先进的一种算法，其结构中每层神经元都只作用于下层神经元[8]，不会出现连续或跳级现象，且各神经元之间不存在相互作用。在服装制版系统参数量化模式识别模型设计中，首先对服装制版系统参数样本数据进行训练，然后借助该算法中的正向传播和反向传播实现模型的设计。

假设神经网络中含有L层神经元和n′个节点，通过Sigmoid函数[9]将神经元中的输入信息依次映射到输出端，输入的信息样本为服装制版系统参数。若只存在一个输出端口，则当输入第k个样本时，节点j的输出可表示为

(11)

对应神经层的第j个节点输出

(12)

将误差函数表示为平方模型，获取服装制版系统参数的最终输出：

(13)

根据式(13)构建服装制版系统参数量化模式识别模型：

(14)

式中：N为服装制版系统参数样本数量；δjk为输入层与输出层连接阈值；k为常数。

2.2 服装制版系统参数量化模式识别模型求解

在上述服装制版系统参数量化模式识别模型中，由于BP神经网络构建的模型在寻优过程中易获取局部最优解，影响服装制版系统参数量化模式识别结果，故引入小波分析对服装制版系统参数量化模式识别模型求解，以获取全局最优解。通过一维离散小波变换识别模型中的高、低频部分，以确定服装制版系统参数量化模式识别的初始数据变化趋势[10]。

首先，对服装制版系统参数量化模式识别模型中的初始数据进行小波分解：

X(t)=pijX(t)+qijX(y) ，

(15)

式中：X(t)为小波分解流程；pijX(t)为服装制版系统样版图像的低频部分；qijX(y)为服装制版系统样版图像的高频部分。其中：

(16)

(17)

式中：C1k为阈值；φ1k为控制图模式原始数据；D1k为小波函数的有效支撑长度；Θ1k为小时聚阶数。

对服装制版系统参数量化模式识别模型的参数进行分解后，将其表示为一维离散小波的多层分解形式：

(18)

式中：pmX(t)为正交系数；qmX(t)为紧支系数；Cm，kφm，k为支撑宽度；Dm，kΘm，k为正态分布的期望值。

式(18)中的支撑宽度

Cm，kφm，k=HCm-1。

(19)

将一维离散小波变换后的参数量化模式初始数据划分为低频部分与高频部分，设定一维离散小波变换的近似系数为模型寻优因子，输出服装制版系统参数量化模式识别模型中的隐藏层节点：

(20)

式中：yi为隐藏层节点输出；ωij为模型权重；θj为参数修正值。

此时，求解服装制版系统参数量化模式识别模型的输出误差，即可得到该模型的最优解，完成服装制版系统参数量化模式识别：

(21)

式中：tk为服装制版系统参数量化模式识别模型的最优解；Oi为分解系数。

3 实验与结果分析

3.1 实验方案

为验证所提方法的有效性，本研究进行了仿真实验。实验在Windows 10操作系统下展开，利用开源数据挖掘工具Weka 6.0实现数据处理与分析，并通过Java语言实现。为保证实验效果，需要获取实验中识别的样本(图2)。实验指标分别为识别准确率和服装残次率。

图2 识别样本图像Fig.2 Identification of the sample images

3.2 结果分析

为了验证本方法的有效性，选取文献[3]和文献[4]方法作为对比，分别对样本服装进行模式识别，识别的面积越大代表识别准确率越高，结果如图3 所示。

分析图3可知，采用3种方法所得到的整体识别覆盖面积存在一定差距。其中，采用本方法得到的样本识别覆盖面积在90%以上，而采用其他两种方法得到的覆盖面积均小于本方法。这是因为本方法借助人工智能算法构建识别模型并获取了最优解，进而提升了识别准确率。

图3 用不同方法所得样本识别准确率对比Fig.3 Comparison of the accuracy of sample recognition by different methods

为进一步验证本方法的有效性，分析了采用3种方法所得的服装残次率，并将测试结果与实际生产中的残次率进行比较，结果如表1 所示。

表1 采用不同方法所得的服装残次率对比Tab.1 Comparison of clothing defective rate of different methods

分析表1可以看出，随着识别样本维度的不断升高，采用3种方法所得的服装残次率均呈上升趋势。其中，采用本方法所得的服装残次率较其他两种方法低。与实际生产中的残次率相比，采用3种方法所得的服装残次率与实际均存在一定差异。其中，采用本方法所得的残次率与实际最为接近，而采用其他两种方法所得的残次率与实际偏差较大。这是由于本方法在进行服装制版之前对获取的参数特征进行了预处理，并根据构建的服装制版系统参数量化模式获取了最优解，实现了服装制版最优，进而降低了服装生产的残次率。

4 结语

针对传统模式识别方法存在的误识率较高、运行时间较长等问题，本研究结合小波分析、BP神经网络对服装制版系统参数量化模式进行识别，并用仿真实验证明了本方法具有较好的识别效果。