离心泵启动过程内部流动特性分析

马晓堂，王 宾，宋文武

（1.西华大学能源与动力工程学院，成都610039；2.四川省水利职业技术学院，成都610039；3.流体及动力机械教育部重点实验室，成都610039）

0 引 言

离心泵是一种农业和工业上广泛使用的流体机械。离心泵在快速启动过程中其表现出区别于稳态过程的特殊性质，在瞬态操作过程中，转速、流量、压力等各个性能参数在短时间内发生剧烈的变化，即泵的工况点在较大范围内以及短时间内发生剧烈的变化。研究离心泵的快速启动过程中离心泵的特性，对整个启动过程可能产生的不稳定影响分析，比较离心泵整个启动过程不同时刻的振动、流动不稳定，以及对系统产生的冲击作用，这是对整个离心泵的启动过程研究十分重要的。

目前，国内外对于离心泵在启动过程的研究相对较少，更多关于启动过程方面的研究在于涡轮机械，郭佳［1］等以某型汽轮机组高速轴系为研究对象，搭建转子瞬态动力学模型，研究其瞬态转子动力学特性，构建高速轴系模型，分析轴系的振动特性，结果表明，在转子升速速率由0提高至1.74 rad/s2过程中，高速轴系各节点临界转速提高0.4%至3.6%，升速过程中高速轴系各节点的振动峰值也有明显增长，最大增幅0.035 mm；针对燃气轮机的启动过程，Yunis M 等［2］通过准稳态方法进行了建模研究。该模型可用于计算启动过程中燃气轮机的最小转矩要求，分析不同大气温度及海拔下的启动特性；Kim J 等又针对重型发电用燃气轮机启动过程的动态特性进行仿真分析［3］采用修正的逐级叠加法估计压气机特性，将压气机所有级数划分为前中后三阶段，分别用不同的曲线刻画低转速特性，结果表明转速对燃气轮机启动过程稳定性的重要作用。少数专家学者也对于离心泵启动过程动态特性方面一些相关的工作，李伟等人［4-5］以瞬态外特性试验性能参数为依据，对启动过程3种转速下的速度矢量、压力场分析，发现准稳态计算扬程呈现直线上升趋势，并随着体积流量的增大逐步偏离试验扬程，3种转速下泵内压力具有相同的增长趋势，叶轮进口截面相对速度矢量近似满足相似定律；叶道星［6］通过多项式建立了流量与转速随惰转时间的数学模型，采用数值计算和量纲分析的方法研究了核主泵的性能变化，发现流量比随着惰转时间的增加迅速下降，在220 s 时降低至6.5%；杨阳［7］基于数值计算与试验研究的方法，对高速深井泵在不同转速下的外特性与内部流场规律进行了系统研究，完成了三种不同的转速变化方案下该深井泵模型的非定常数值计算，发现直线加速过程与开口向下的二次加速过程中扬程的波动要弱于开口向上的二次加速过程，且开口向下的二次加速过程能够最先达到扬程要求；Tsukamoto 等人［8，9］对小型离心泵进行了快速启动和停机试验，到最大转速1 500 r/min的启动时间约为0.15 s；其后，Lefebvre等人［10］在一个闭式试验台上进行了启动试验，到最大转速2 000 r/min 的启动时间约为0.6 s；吴大转等人［11-16］对离心泵进行了启动试验和数值模拟，发现在转速到达最大值附近，瞬态扬程明显小于准稳态预测值，且不同加速度下两者的偏离明显不同。

综上所述，目前对于离心泵整个启动过程的内部流动以及非定常研究相对较少，没有成熟的理论体系为整个离心泵启动过程进行水力优化进行指导。本文以一台比转速为146的中比转速离心泵为研究对象，利用CFD 软件通过全流道三维定常和非定常数值模拟，研究离心泵启动过程每时段内部流道压力分布以及隔舌与叶轮流道压力脉动情况，为今后离心泵水力优化以及离心泵启动怕配套电机选择，机组的安全可靠运行等方面具有一定的指导意义。

1 计算模型及网格划分

1.1 几何模型参数

本文通过运用UG 建立离心泵的三维实体模型，为了确保计算模型中的湍流发展更加稳定提高模拟结果的准确性，对泵的进口段和出口段进行适当的延伸，延伸长度为进、出口段的5倍直径；其参数如表1所示，三维模型如图1所示。

表1 离心泵主要设计参数Tab.1 Main design parameters of centrifugal pump

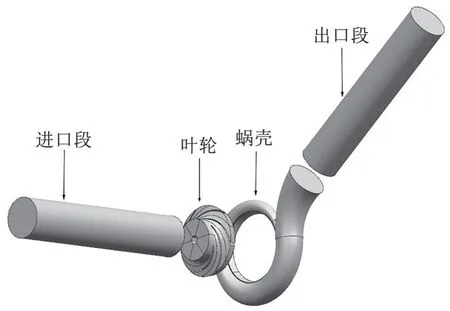
图1 离心泵三维模型图Fig.1 3D model diagram of centrifugal pump

1.2 网格划分与无关性分析

对于多曲面几何模型的离心泵，本文采用适用性相对较好的非结构四面体网格，为保证网格质量和计算的精准性，在叶轮叶片的进口、叶片的表面、隔舌等位置都进行了网格加密。并对网格进行无关性验证，根据表2 所示，随着网格数的增加，泵的效率先增大，最后逐渐趋于平缓，如表2 所示；当网格数目达到3 783 873时泵的效率基本不再受到网格数的影响，为了方便计算节约时间，最终确定本次模拟计算网格数为方案3，网格图如图2所示。

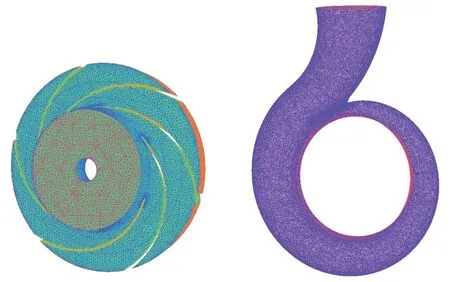
图2 叶轮和蜗壳的网格图Fig.2 Grid diagram of impeller and volute

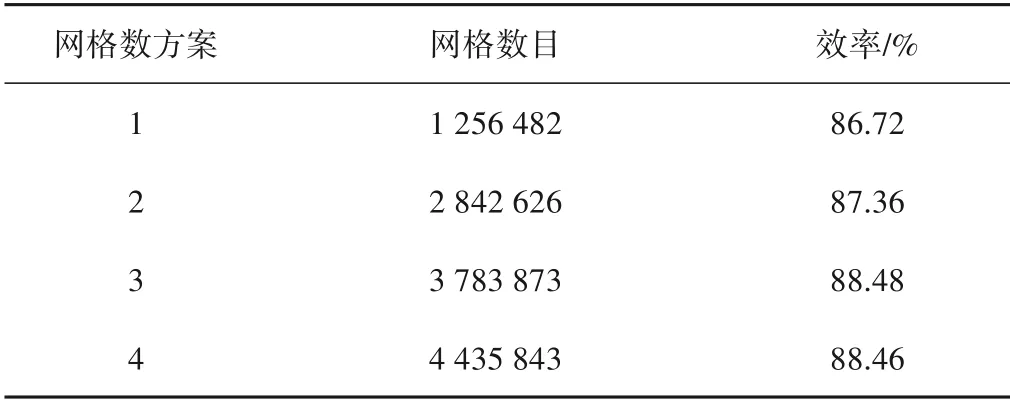
表2 网格无关性验证Tab.2 Grid independence verification

2 数值计算方法

2.1 计算方法与边界条件

本文采用RNGk-ε模型对离心泵启动过程的定常和非定常进行数值模拟。考虑到离心泵启动过程是一个变速过程，结合已有文献［8-10］研究结果，以及张玉良［17，18］文献，引入启动过程转速公式：

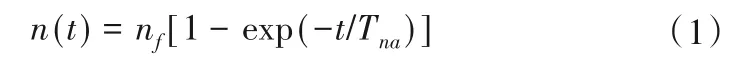
式中：nf是启动结束后的稳定转速，本次研究中为1 450 r/min；Tna是名义加速时间，定义为转速从静止上升到最终转速的63.2%所花费的时间，本次根据文献［18］取为0.1 s。

考虑到在泵转速变化过程中，流量随着转速的变化而变化，因此在设置边界条件时需要通过自定义表达式控制流量的不断变化。根据已有文献资料［7］研究情况，本文中流量的变化规律按照相似定律中流量与转速之间的关系得到：

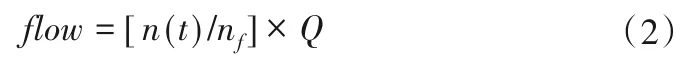
式中：Q为设计流量160 m3/h。

计算边界条件中进口条件设置为Total pressure，参考压力设置为1 atm，出口边界条件设置为Mass flow［19，20］。网格节点均采用GII模式，对于叶轮和进口、叶轮与蜗壳之间的动静耦合交界面，采用Frozen Rotor模式进行衔接，其壁面为无滑移壁面，其他壁面均采用静止无滑移壁面，收敛精度为10-5。在非定常模拟中，动静耦合界面采用Transient Frozen Rotor 模式。以定常计算结果作为非定常计算初始条件，在保证计算精度的前提下，根据转速变化情况设置计算总时间和输出频率［21］。

2.2 压力脉动监测点设置

为了分析离心泵启动过程中内部瞬时的状态，以及内部压力脉动的影响，在离心泵叶轮流道、隔舌处设置监测点y1～y5和监测点G1～G4；其中叶轮流道上的监测点随叶轮一起转动，而隔舌位置的监测点则是固定位置。

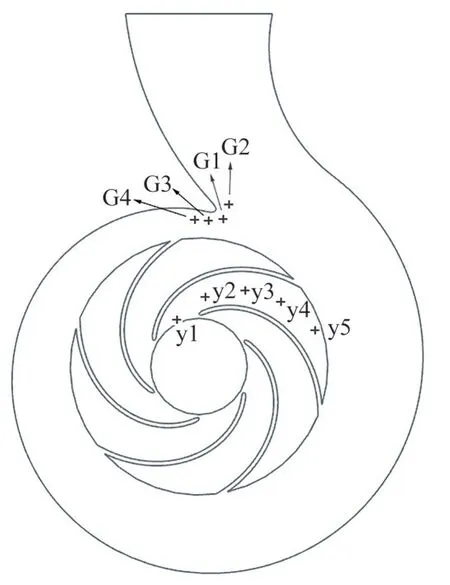
图3 监测点位置Fig.3 Position of monitoring point

3 结果分析

3.1 外特性分析

图4为该离心泵在启动过程中的转速变化曲线和通过相似定律中流量与转速的关系得到的启动过程转速和流量的曲线；图5为该离心泵在数值模拟启动过程阶段的外特性曲线和通过相似换算后得到的设计扬程曲线。

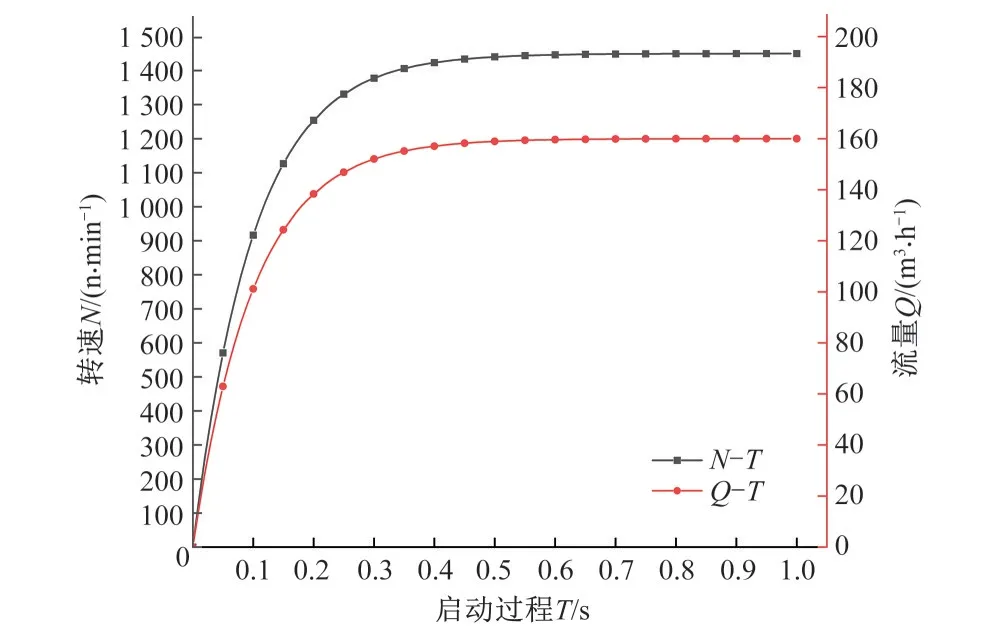
图4 转速流量启动过程曲线Fig.4 Start process curve of speed and flow

由图4可知随着转速的逐渐增加离心泵的扬程和效率也随着增加，当达到0.5 s之后增加趋势逐渐平缓，在1 s时刻达到最高稳定值，增加趋势和理论走向一致且模拟扬程和设计扬程重合性较好，满足相关的水力机械流动规律，证明本次研究模拟方法具有一定的可靠性，数值计算模拟合理［22］。

其中因本次研究对象离心泵比转速大于65 应用斯基克钦公式计算理论扬程［23］：

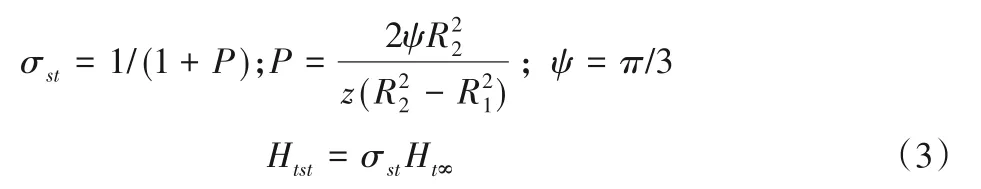
式中：R1、R2为叶轮进、出口半径；Z为叶片数；Ht∞=u2vu2，vu2由无滑移的出口速度三角形求得，设vu1为0。

对图5 分析对比发现0.1 s 时刻之前，离心泵处于快速启动过程，在此段时刻中实际模拟曲线高度贴近理论扬程曲线，这由于在启动初始阶段随着叶轮转速的快速增长，扬程效率曲线也快速增长，但是叶轮并未达到高速稳定工作，而在0.4 s 后模拟扬程高于理论扬程，转速达到额定转速的98.17%，能够达到转速稳定，满足离心泵在某些特定工况下正常工作。

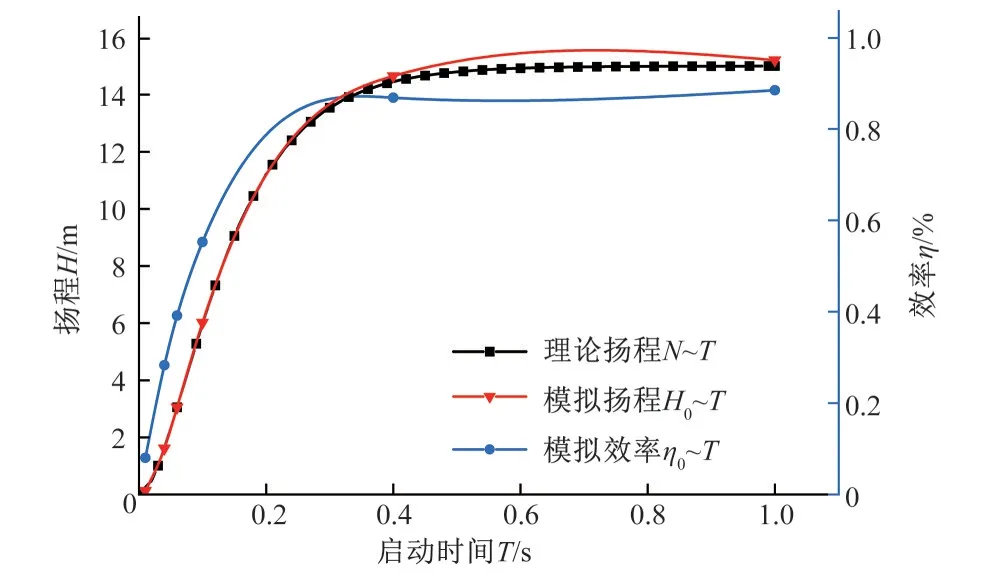
图5 模拟计算外特性及扬程比较曲线图Fig.5 Simulation calculation of external characteristics and head comparison curve

3.2 离心泵内部流道压力分布

启动过程中不同时刻离心泵内部流道中截面压力分布如图6所示。

由图6 可知，在离心泵的整个启动过程中压力分布是一个从小到大的过程。0.1 s时刻是压力分布的变化明显的分界点，在0.1 s之后离心泵内部流道压变化突增，离心泵达到一种不稳定状态；这是由于转速在0.1 s时刻达到稳定转速的63.2%，整个离心泵内部流量超过额定流量的50%，内部流动不稳定。通过图6的对比分析，0.1 s后的启动过程相对更剧烈，在检测泵启动过程应重点关注0.1s 之后离心泵的非稳定情况。在今后的研究中应主要对离心泵启动过程中的快速变化阶段进行研究。

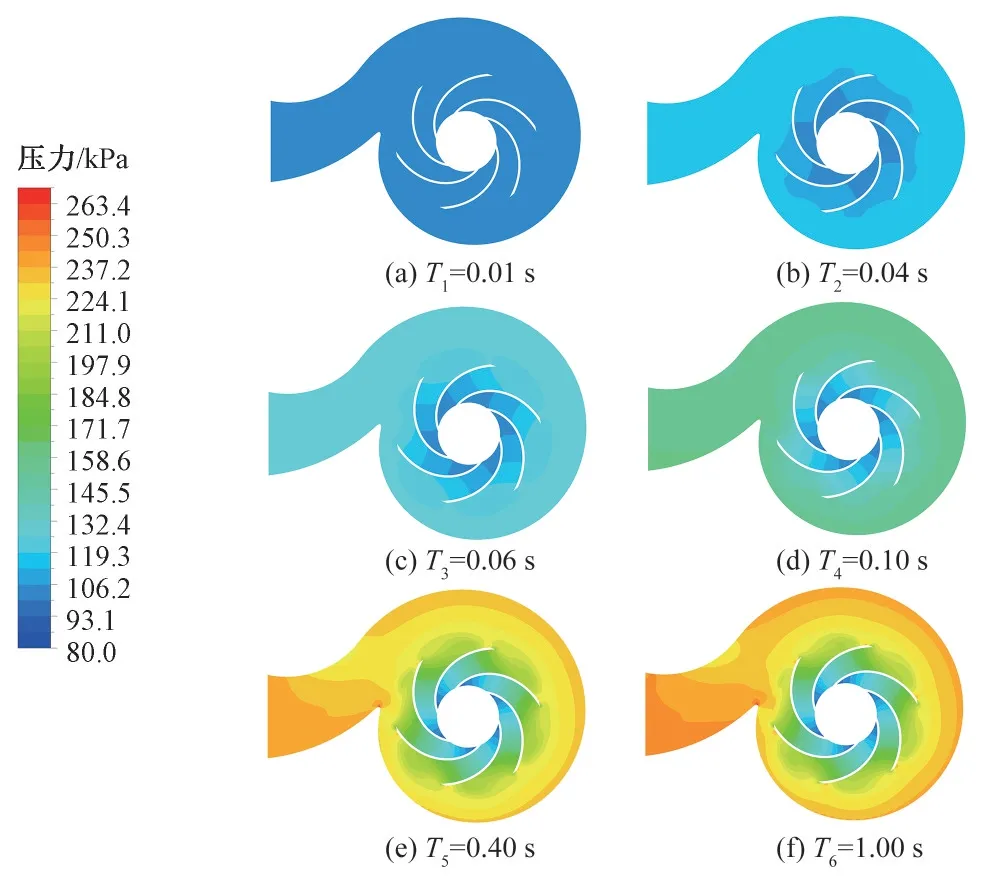
图6 不同时刻离心泵内部压力分布Fig.6 Pressure distribution inside the centrifugal pump at different times

3.3 压力脉动分析

考虑到整个离心泵启动连续过程的数据处理十分繁杂，在保证模型准确性的前提下，将整个连续过程简化为某时刻的点过程，对启动阶段6个不同时刻的压力脉动进行研究，计算步长为对每应时刻离心泵旋转1°的时间计算分别为Δt1=1.207 85×10-3s、Δt2=3.486 48×10-4s、Δt3=2.547 55×10-4s、Δt4=1.818 36×10-4s、Δt5=1.170 87×10-4s、Δt6=1.149 42×10-4s，用6 个时刻对应转速计算模拟10 个非定常周期总时间分别为ΔT1=1.207 85×10-2s、ΔT2=3.486 48×10-3s、ΔT3=2.547 55×10-3s、ΔT4=1.818 36×10-3s、ΔT5=1.170 87×10-3s 和ΔT6=1.149 42×10-3s，取最后5 个周期进行分析，从而推测整个连续过程中离心泵内部可能存在的状态。

针对所有监测点进行观察，发现其中G1 和y5 两处监测点的压力脉动最为明显，故选取这两个监测点的数据进行分析比较。通过图6发现离心泵隔舌区域的压力逐渐增大并在离心泵达到相对稳定后开始集中，叶片尾部则在1 s 时刻出现压力集中，针对这些现象对隔舌区域和叶轮流道进行压力脉动测定，推测分析整个启动过程其区域的压力脉动情况以及可能对离心泵的性能产生的影响。

对数据处理后发现，启动过程的不同时刻对应转速在同一隔舌部分监测点G1压力脉动情况如图7所示。其中，叶轮额定转速为1 450 r/min，轴频率为f=24.17 Hz，叶频fi=145 Hz；T6=1 s，T5=0.4 s，T4=0.1 s，T3=0.06 s，T2=0.04 s，T1=0.01 s，但考虑到每时刻对应的转速不同，将每个时刻的转速对应的叶频通过频率，进行归一量化处理。

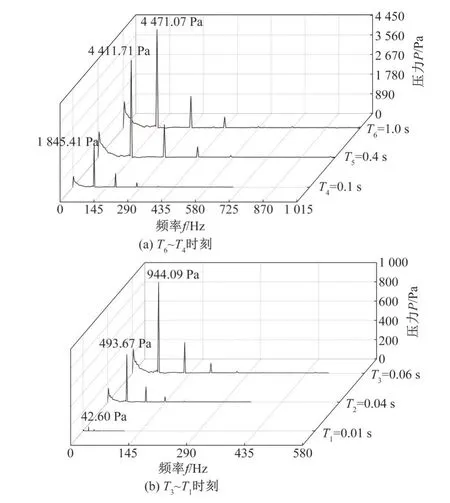
图7 不同启动时刻隔舌位置压力脉动频域图Fig.7 Frequency domain diagram of pressure pulsation at tongue position at different starting times

从图7 可知，隔舌位置监测点在不同时刻的压力脉动变化规律为：当离心泵启动到1 s阶段稳定时，脉动主频为叶频fi，而其他时刻脉动主频均达不到一倍叶频，T5、T4、T3、T2和T1分别为0.98fi，0.63fi，0.45fi，0.33fi和0.10fi，与相对应时刻转速与额定转速倍数关系相同；其中次频也满足以上相同规律；但进行归一量化处理后发现每时刻的压力脉动主频产生位置均为相应时刻的一倍叶频处。说明在启动初始过程中，离心泵隔舌位置处会出现低频压力脉动，并且在0.1 s 前脉动幅值相对较低，0.1 s后脉动幅值急剧增大，并且每时刻压力脉动主频均产生于一倍叶频处。

图8则是叶轮流道尾部出口处的压力脉动随着启动时间的变化情况。叶轮流道出口压力脉动随着启动时间的增加，压力脉动也逐渐增加，当达到1s 额定转速时，此时脉动主频出现在轴频f，其他时刻主频分别为0.98f，0.63f，0.45f，0.33f和0.10f；归一量化后每时刻的压力脉动主频产生位置均为相应时刻的一倍叶频处。随着时间的增加，离心泵启动过程中的压力脉动也随之增加，并且在0.1s转速达到额定转速的63.2%之后，内部压力脉动出现剧烈增加。

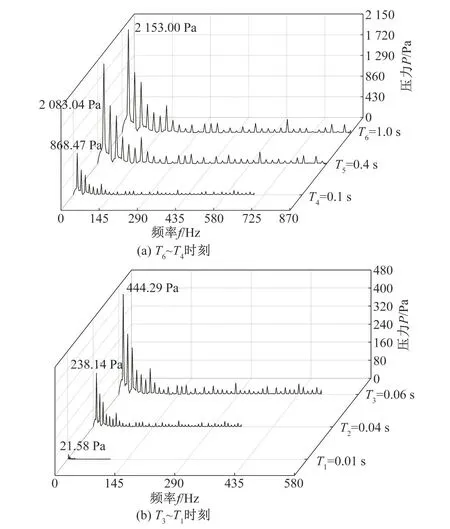
图8 不同启动时刻叶轮出口压力脉动频域图Fig.8 Frequency domain diagram of impeller outlet pressure pulsation at different starting times

由图7、8 将每个时刻的转速对应的叶频通过频率，进行归一量化处理后，发现在不考虑其他外来因素的影响下，离心泵启动过程中离心泵内部产生压力脉动的主要原因是由于离心泵叶轮的旋转与静止隔舌位置产生的动静干涉所造成。

从图9 可知，启动阶段任意时刻隔舌位置处的最大压力脉动均大于叶轮流道出口处，并且两处压力脉动均在0.1 s后开始急速上升。

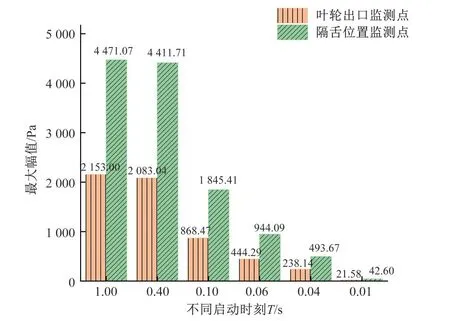
图9 不同启动阶段两处监测点压力脉动最大幅值Fig.9 The maximum value of pressure pulsation at two monitoring points at different starting stages

分析原因：首先在启动过程低转速阶段，转速未达到离心泵工作转速，内部流量相对较小，内部流动出现回流不稳定，引起压力脉动；而在转速达到额定转速63.2%之后，整个离心泵达内部流量也超过额定流量的50%，离心泵内部增加流动碰撞，更加紊乱引起更剧烈的压力脉动。因此今后在研究离心泵启动过程的稳定性时，更应该对转速达到额定转速63.2%之后进行详细研究拓展。

3.4 不同启动阶段内部径向力分布

图10、图11为离心泵启动过程中6个不同时刻对应转速非定常叶轮以及隔舌的径向力分布情况。从图上可知，作用在叶轮上的径向力均呈现为6 片花瓣形状分布，而作用在隔舌位置的径向力则呈现六边形形状分布。随着时间的增加离心泵内部径向力逐渐缓慢增加，在0.1 s 后开始剧烈的增加，增加幅度出现较大的提升，且当达到0.4 s 时刻，此时离心泵内部径向力分布已经和稳定状态时刻的径向力大小以及形状基本保持一致。

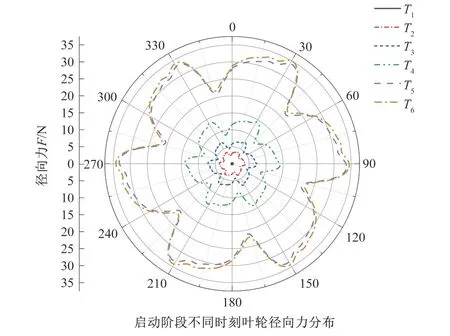
图10 启动阶段不同时刻叶轮径向力分布Fig.10 Radial force distribution of impeller at different starting stages

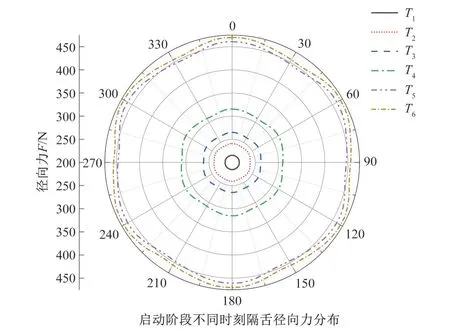
图11 启动阶段不同时刻隔舌径向力分布Fig.11 Radial force distribution of the tongue at different starting stages

4 结 论

通过对一台比转速为146的中比转速离心泵的启动过程的内部现象和非定常数值模拟分析，得出以下结论。

（1）离心泵启动过程中，0.1 s 时刻转速达到额定转速数的63.2%后离心泵效率和扬程上升情况变缓，当达到0.4 s 时离心泵扬程已经到达稳定时刻的96.4%，整个离心泵内部基本以达到稳定状态。

（2）在离心泵的整个启动过程中内部压力是一个从低到高的一个过程，在0.1 s 之前整个离心泵内部都属于低压时刻，0.1 s 之后内部压力出现跳跃式的增加，离心泵达到一种不稳定状态。

（3）随着启动时间的增长，隔舌位置脉动主频逐渐向叶频靠拢；叶轮流道出口压力脉动也逐渐增加，当达到1 s 额定转速时，此时脉动主频出现在轴频f，其他时刻均达不到一倍轴频f；将每个时刻的转速对应的叶频通过频率，进行归一量化处理后，发现离心泵内部的压力脉动主要由动静干涉产生；并且启动阶段任意时刻隔舌位置处的最大压力脉动都大于叶轮流道出口处，并且两处压力脉动都在0.1 s后开始急速上升。

（4）叶轮和隔舌位置的径向力随着启动时间的增长，径向力逐渐增大，当达到0.1 s 时刻后径向力出现剧烈增长，而达到0.4 s 时刻后径向力与稳定状态时刻的径向力大小以及形状基本保持一致。 □