基于多列深度神经网络的电力负荷预测模型

童文术， 王枫， 周斌， 黄文杰， 靖海， 朱小波

(1.国网湖北省电力有限公司，湖北 武汉 430077；2.湖北华中电力科技开发有限责任公司， 湖北 武汉 430077)

0 引 言

当前我国输配电电能质量受到用电负荷需求的影响较为显著。当负荷需求大于供给能力时，电网工频下降，反之，电网工频上升。同时，用电负荷如果与电能供应之间存在较大差值，还会影响到电网的电压，引起各种次生电网故障[1]。因此，在当前电网运行策略下，发电站的电力供给能力必须严格按照电网负荷需求进行调整，确保电网的电能供给量与电网负荷需求量之间形成匹配。而如果要形成这种匹配关系，还应考虑电网电能供给量的调整效率和调整时间滞后性，这就需要对电网负荷需求量的数据进行一定前瞻量的预测[2]。

传统的数据预测算法，多采用曲线估计法，该算法是在大量前置数据的支持下进行曲线拟合，进而通过对拟合曲线的延伸，获得向前若干周期的预测数据[3]。或采用模糊矩阵深度迭代法，使用多组模糊矩阵相互配合，从之前数据的模糊矩阵特征结果中发现数据规律并作出数据走向判断或者数据预警[4]。但是，前者一般只支持向前约5%～10%周期的较高精度和较高信度的数据估计，即如果分析1 h的前瞻数据，则需要至少10 h时的前置数据量。且前者几乎无法对数据的前瞻拐点进行有效判断。而后者只能判断数据趋势，难以实现对前瞻精准数据值的有效预测[5]。

随着人工智能技术快速发展，基于浮点集群设备(GPU)和逻辑集群设备(TPU)的计算中心机组在电力系统中得到越来越广泛的部署，使用基于机器学习的人工智能技术对未来6～12 h电力负荷数据进行有效预测，成为当前电力负荷管理的重点数据技术突破方向。

1 电力负荷曲线的数据特征分解

1.1 电力负荷特征提取的基本算法

对于北京等一线城市来说，因为城市职能的划分，不同区县的电力负荷变化情况各有不同，如昌平区、房山区和怀柔区等边远区县，其夜间用电峰值显著高于日间;东城区和西城区等市中心区县，则其日间用电峰值显著高于夜间；大兴区和丰台区等工业较发达且兼顾居住区的曲线，其每日用电峰值的变化则不显著。早期对电力曲线峰值进行计算的过程中，一般就每日用电峰值的日夜周期和季节周期进行归类，如大部分用电环境下，夏季及冬季的用电峰值较高，而春季和秋季的用电峰值较低。因为区域经济特征，商业办公区的日间用电峰值较高，居民区的夜间用电峰值较高，工业区的用电峰值受到电费分时政策的影响较为显著。因此，早期城市电力负荷调度过程中，一般利用电费分时政策有效引导工业区用电时段以平衡区域内的其他用电峰值对当日用电峰谷差的影响。在机器学习条件下，电力负荷曲线的特征提取方式在该模式下较难操作，应该采用谐波特征法、频率提取法和工频控制法等获得量值化电力负荷特征标志的提取方式，如图1所示。

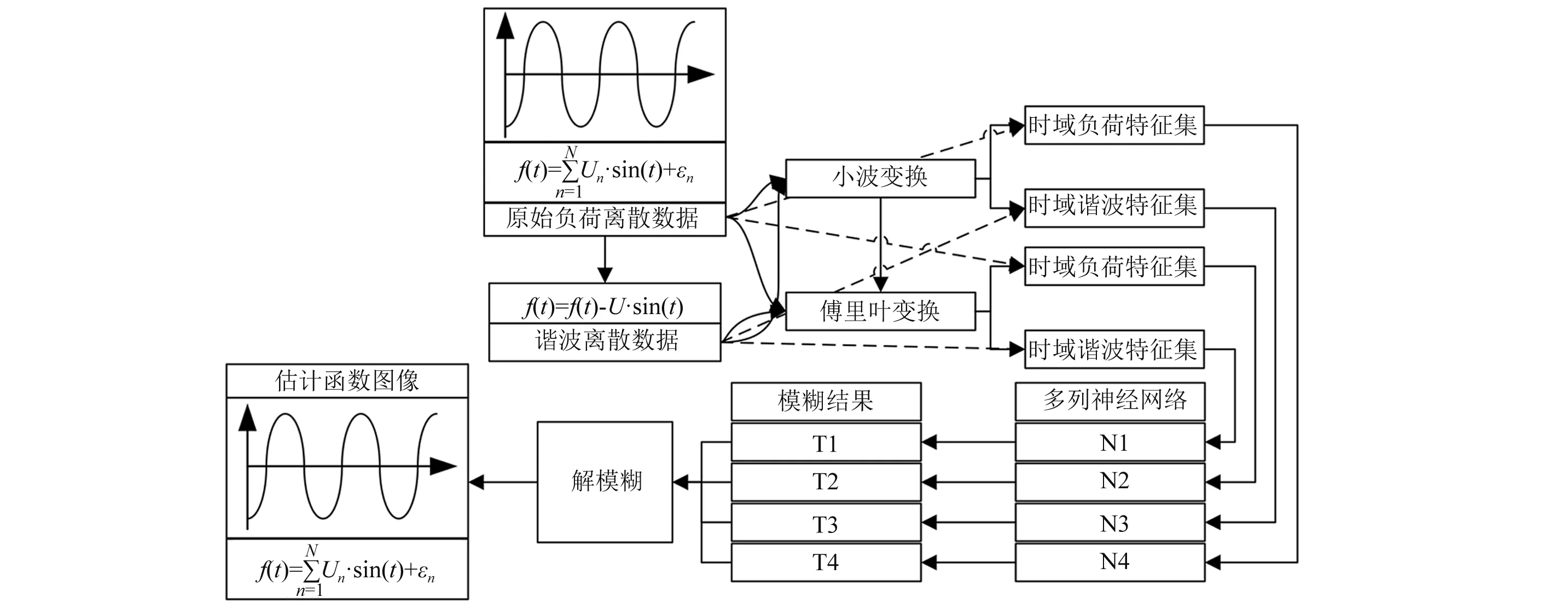
图1 机器学习条件下的电力负荷特征提取模式

图1中：首先通过负荷波形的离散数据中减去理论负荷的有效值得到谐波状态离散数据，将两组数据分别进行小波变换和傅里叶变换，分别得到时域特征和频域特征。对4组特征集分别进行基于神经网络的机器学习计算，得到其模糊分析结果，对4列数据的模糊结果进行综合解模糊，将数据合并成最终的估计函数图像。该提取模式的统计学意义是最终实现基于多列三角函数图像叠加的深度迭代回归结果，从而在此基础上对未来负荷状态进行三角函数曲线估计。

该特征提取后的直接结果为：

(1)

式中：N为叠加正弦函数的数据列数量；Un、In为第n列叠加波形的等效电压及等效电流；εn为第n列叠加波形的等效相位角；βn、γn为回归函数的斜率和截距校正值。

1.2 数据特征的提取算法

在离散数据中，规划理论负荷波形值，其电压波形为：

(2)

其电流波形为：

(3)

式中：Uo、Io为额定电压和额定电流；λ1、λ2、λ3为频率调整变量，此处工频按照50 Hz计算；ωA、ωB、ωC为三相相位角修正值，此处按照三相各相距120°计算。

通过式(2)、式(3)得出的时刻t对应的理论负荷值，与实际发生值作差值，即可得到等效谐波离散数据集。AUTODESK CAE条件下，对离散数据集进行小波变换分析和傅里叶变换分析，可以得到负荷特征和谐波特征的时域、频域特征集结果，共4个特征集。

小波变换分析基函数为：

(4)

式中：fi(t)为波形矢量发生值，可认为fi(t)=f(ti)→f(ti-1)，即f(t)序列下，第i个发生值与第i-1发生值之间的数据空间坐标矢量；αi为去矢量化系数，不同小波分析策略下，该系数可以进行调整并予以含义赋值。

小波变换分析的统计学意义在于发现离散数据的波形关系曲线，特别用于获取离散数据之间的时域波形曲线。

傅里叶变换分析基函数为：

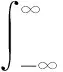
(5)

式中：f(t)为小波分析中获得的时域函数；-iωt为傅里叶常数；e为自然常数。

傅里叶变换的统计学意义在于发现时域函数特征下的频域特征值。

2 多列神经网络的设计

2.1 多列神经网络的总体设计

多列神经网络能有效缓解大宗并列数据输入神经网络模块时发生的神经网络输入层过于冗余庞大,且数据关联度不高影响神经网络输出结果精确度的问题。且多列神经网络可以对外提供多个并列输出结果。

本文将等效电压数据、等效电流数据分别进行时域和频域特征的提取，形成共8个多列神经网络，如表1所示。

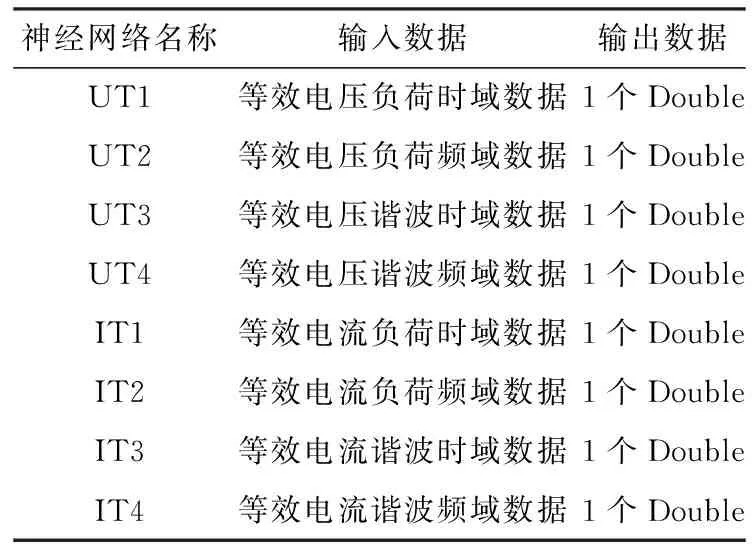
表1 多列神经网络的功能布局图

所有时域数据和频域数据均是经过小波变换或傅里叶变换后的函数特征结果。如果在神经网络中通过相应函数图像直接输入，就涉及函数图像量值化的过程。早期工程实践表明，单一模块的神经网络对函数图像直接量值化的过程信度并不高，因此还需要对这些数据在神经网络之外进行量值化。而等效电压和等效电流并不需要对三相电流和三相电压进行分别控制，而是针对单独回路计算等效电压和等效电流后对等效负荷进行控制。

从式(1)分析需求中可以看到，嵌套1层三角函数条件下，电流和电压数据共需要8个待回归变量，而达到4层三角函数条件下，电流和电压数据共需要32个待回归变量。故在上述第一层多列神经网络之后，仍需要进行第二层多列神经网络分析过程。第二层多列神经网络分析过程需要32列神经网络模块，数据来源为上述8个输出结果。如图2所示。

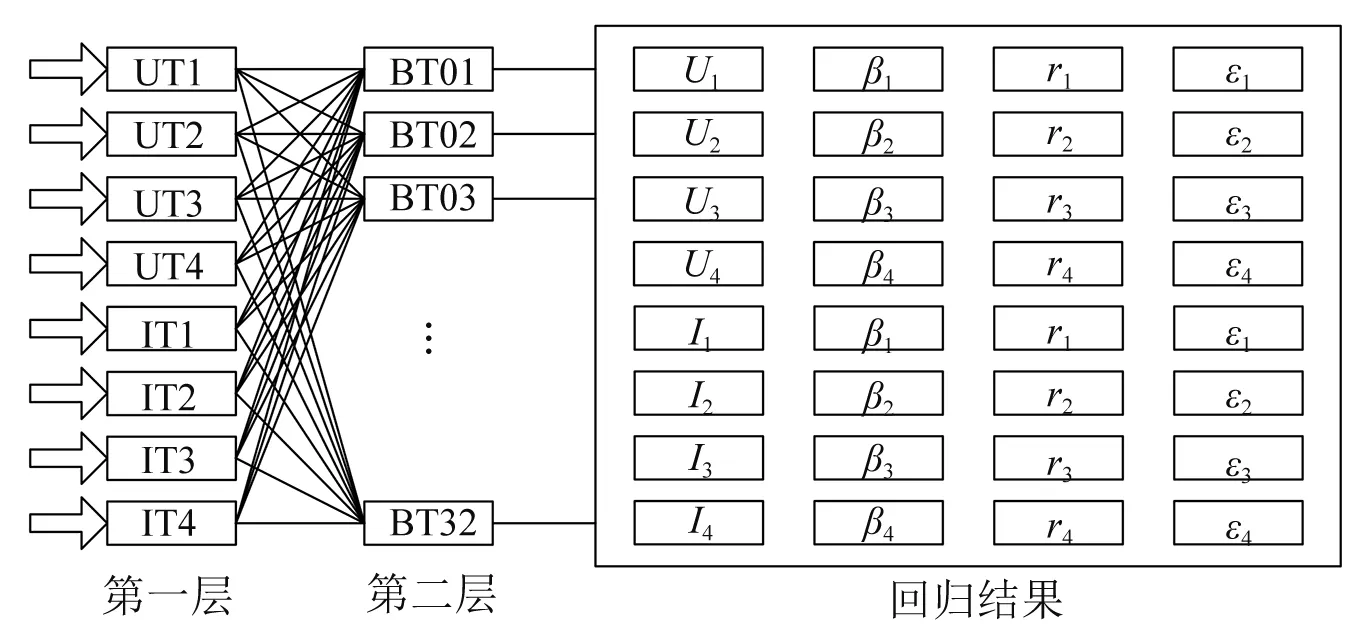
图2 多列神经网络的2层结构图

图2中，使用第一层多列神经网络实现数据的基本准备，并对第二层提供8个Double格式的输入值，第二层多列神经网络在第一层多列神经网络提供的数据基础上，形成32个输出值，这32个输出值可以直接用来作为式(1)待回归变量的赋值使用。

2.2 神经网络模块设计

第一层的8个模块的统计学意义基本一致，第二层32个模块的统计学意义基本一致，故两层神经网络模块可以进行统一设计。

1)第一层多列神经网络节点设计

第一层多列神经网络的统计学意义是将大宗输入值进行归一化处理，且综合放大细部信息，实现对数据的有效整合。故计划将每个模块设计为5层。按照输入值500个周期数据计算，输入层共500个节点，且输出仅为1个Double数据，故隐藏层的5层：第一层设计500个节点，第二层设计220个节点，第三层设计97个节点，第四层设计31个节点，第五层设计7个节点。

隐藏层第一层及第二层的统计学意义是数据的进一步归一化，故为了进一步节约计算中心算力，使用线性回归法对节点函数进行设计：

Y=∑(AXi+B)

(6)

式中：Xi为输入变量集；Y为输出结果；A、B为待回归变量集。

隐藏层第三层及第四层的统计学意义是充分放大细部数据，使细部数据相对关系得到充分放大的同时不影响数据的前后关系。故其应采用对数回归法进行节点函数设计：

Y=∑(AlogeXi+B)

(7)

式中：Xi为输入变量集；Y为输出结果；e为自然常数；A、B为待回归变量集。

隐藏层第五层的统计学意义是进一步对数据规律进行整合，获得χ2值更小的回归关系拟合，故其应采用多项式回归函数进行节点设计。

(8)

式中：Xi为输入变量集；Y为输出结果；Aj为第j阶多项式条件下的待回归变量。

2)第二层多列神经网络节点设计

第二层多列神经元网络的统计学意义是将深度模糊化的第一层多列神经元网络输出数据进行解模糊。即32列多列神经元网络每一列都是在第一层多列神经元网络的8个输出值中精确提取深度叠加三角函数的待回归变量。

因为第二层多列神经元网络的输入值仅为8个Double数据，与第一层数百个输入值有所不同，所以第二层多列神经元网络的每个节点的输入层8个节点，输出层1个节点，其隐藏层去除了深度归一化过程，可以设计得更加简单。故采用3层隐藏层设计，分别为19节点、27节点和5节点。

隐藏层第一层的统计学意义是赋予深度归一化数据更多数据细节，即将数据的间距充分拉大且使靠近0数据向±1移动。因此，采用二值化算法进行节点设计。

(9)

式中：Xi为输入变量集；Y为输出结果；e为自然常数；A、B为待回归变量集。

隐藏层第二层和第三层的统计学意义是进一步放大数据细节，依照式(8)对节点进行设计。

第一层多列神经网络和第二层多列神经网络的输入层和输出层，均按照线性回归函数进行节点设计，函数公式如式(6)所示。

综合两层多列神经网络的设计思路，其设计参数如表2所示。

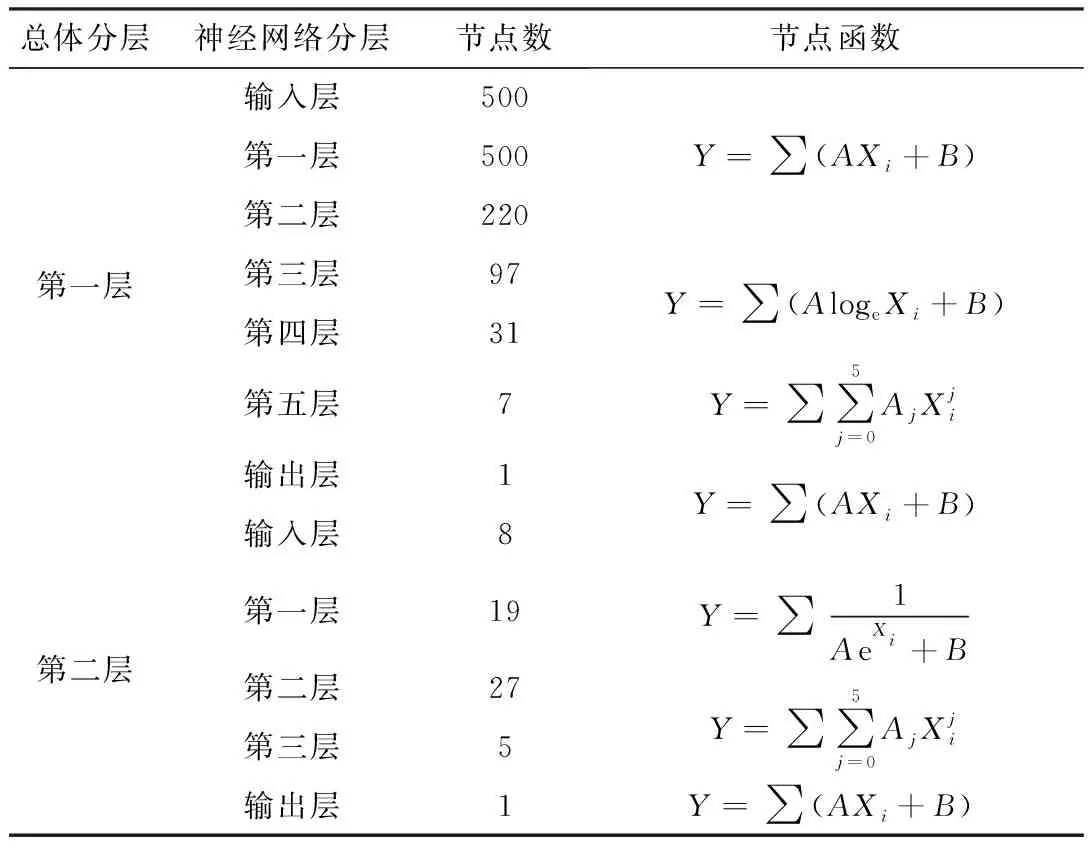
表2 多列神经网络的层次节点设计参数

3 电力负荷预测模型的仿真测试结果

选取2018年6月至2020年6月某市某输电回路电力负荷运行数据，采用移动窗口法选取不同时段数据对本文模型进行仿真测试。共测试数据窗口330个，分别就其1h预测结果，3h预测结果，6h预测结果，12h预测结果进行分析，其误差分布情况如表3所示。

表3 仿真测试数值误差分布结果表 %

表3中，对比前文论述的三种电力负荷预测模型，采用多项式曲线估计法对不同预测周期数值精度的控制。达到3 h预测目标时，其精度仍在±5%以内，但在6 h预测目标下精度已经超过±10%的误差。而深度迭代模糊矩阵法对趋势的预测属于强项，但对数值的预测无法达到工程需求的精度范围。多列神经元网络法的预测值，在达到12 h预测目标时，仍可达到±2%的预测精度，可以满足本文的设计需求。

对负荷趋势的预测准确度方面，仿真测试结果如表4所示。

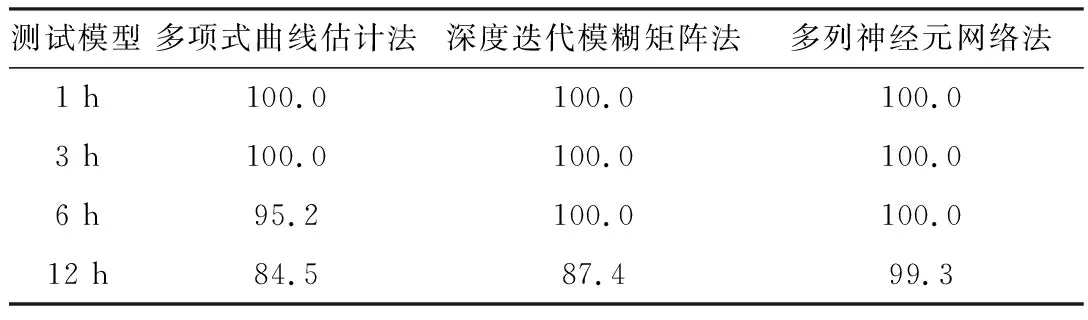
表4 趋势准确度仿真测试结果 %

表4中，对负荷变化趋势的预测结果中，深度迭代模糊矩阵法的预测准确度较多项式曲线估计法有显著优势，但仍略逊色于多列神经元网络法。在使用多列神经元网络法时，对6 h负荷变化趋势的预测精度仍可达到100%准确度，在对12 h预测目标的电力负荷变化趋势预测中，其准确度达到99.3%，高于其他两种预测模型的预测结果。

4 结束语

在离散数据差值治理的前提下，使用小波变换分析和傅里叶变换分析获得数据的4组特征数据，再将电压、电流共8组特征数据进行第一层多列神经元网络分析获得8个特征变量，在此8个特征变量的基础上再进行第二层多列神经元网络分析进行解模糊，进而得到关于电压和电流的等效负荷回归方程。该方程为叠加三角函数方程。在此方程的基础上，可以对电力负荷等变化较为复杂、变化周期较短的数据进行深度回归分析。经过历史数据仿真分析，发现该方法较以往常用的多项式曲线估计法和深度迭代模糊矩阵法，判断准确度和精度均有显著提升。