温度对考虑黏弹性的钢- 橡胶对滚结构动态力学特性的影响

初红艳， 王 瑞， 陈 其， 洪英洁

(1.先进制造技术北京市重点实验室， 北京 100124； 2.北京工业大学先进制造与智能技术研究所， 北京 100124)

橡胶被广泛运用到工业领域当中，例如印刷机胶辊、轮胎、垫圈、密封圈等. 橡胶材料具有超弹性和黏弹性等力学性能. 橡胶材料在使用中，温度的变化会直接影响橡胶制品的结构、性能和使用寿命. 例如印刷机胶辊在挤压旋转中，辊间转动的摩擦生热以及橡胶材料的滞后生热会引起胶辊材料特性的改变，从而影响辊间接触特性，影响印刷质量. 初红艳等[1]通过橡胶的生热实验，分析了温度升高对橡胶力学性能的影响，得出初始硬度大、橡胶层厚度小的橡胶温升大，温升导致橡胶硬度减小；韩传军等[2]采用有限元法分析了常规型和等壁厚橡胶衬套的热力耦合效应,讨论了橡胶温升的物理机理，发现常规型衬套温度场呈椭圆形分布,而等壁厚衬套温度分布较为均匀，温度越高,衬套的热应力和变形就越大，同工况下等壁厚衬套的温升及应力应变均小于常规型衬套；Austrell[3]提供了一种估算滞后生热引起温升的方法，滞后热量由橡胶材料的损耗角、圆周速度以及接触模型中的一些参数计算得到，以此为热源得到橡胶辊的温度分布；孔亚彬等[4]采用含高阶项的Mooney-Rivlin本构模型对丁腈橡胶O形圈/316L不锈钢配副的往复摩擦生热特性进行有限元分析及试验验证，得出不同工况下橡胶O形圈/不锈钢配副的温度分布；黄京城等[5]运用有限元软件Abaqus对12R22.5载重子午线轮胎进行不同行驶速度、负荷、充气压力条件下稳态滚动温度场的数值模拟，得出轮胎高温区域主要分布在胎肩部位和胎圈附近,最高温度出现在胎肩部位,随着行驶速度、负荷的提高,轮胎温度升高,充气压力增大,轮胎温度降低；吕亚男等[6]基于网格应变测试技术，对硅橡胶进行了不同温度下的单向应力应变测试，发现硅橡胶力学性能具有温度相关性，其模量和定伸长下的应力均随着测试温度的升高而降低；赵永玲等[7]对一种橡胶材料进行了不同温度和不同应变幅值下的频率扫描实验,得到了橡胶材料的储能模量、损耗模量和损耗因子随频率的变化情况，对比分析得出高阶分数导数FVMP模型较分数阶Kelvin-Voigt模型能更好描述橡胶材料在不同温度和不同应变幅值下的动态力学行为；Aarts等[8]运用仿真工具确立了柔性胶辊系统轴向压力变化的数学模型，分析了橡胶层厚度、辊长等对压力分布的影响；Jurkiewicz等[9]测量了印刷机胶辊的接触宽度，通过胶辊半径、接触宽度、杨氏模量与泊松比分析了胶辊的压缩变形特性. 上述研究中，在橡胶本构模型建立方面，多应用理论推导的方法；在橡胶温度方面，多分析温度分布，关于温度对橡胶力学特性影响局限于模量改变引起的应力应变，未对其应用产生的影响进行进一步研究；在橡胶辊接触压力、接触宽度等接触区特性分析方面，均未考虑温度的影响.

本文以一对挤压对滚的钢- 橡胶结构为研究对象，通过实验、理论与仿真相结合的方法建立橡胶超弹- 黏弹复合本构模型，分析了橡胶辊在挤压旋转过程中的温度对其黏弹性及动态力学特性的影响.

1 钢- 橡胶结构动态力学特性实验

为得到橡胶辊在挤压旋转过程中的温度以及压深变形量、接触宽度等动态力学特性，进行了钢- 橡胶辊动态力学实验.

所用实验设备为钢- 橡胶辊对滚结构实验平台， 实验平台钢辊与橡胶辊长度均为210 mm，钢辊直径为65 mm，橡胶辊为钢质辊芯外覆盖一层邵氏硬度为50的丁腈橡胶，钢芯直径为45 mm，外覆橡胶层厚度10 mm. 平台具备实时调节两辊间压力与主动辊转速等功能，搭接红外测温仪可连续采集记录辊间实时温度，配备超高速工业微型相机可实现连续拍摄辊间接触状态及变形情况等功能. 实验平台及钢- 橡胶辊截面示意图如图1、2所示.

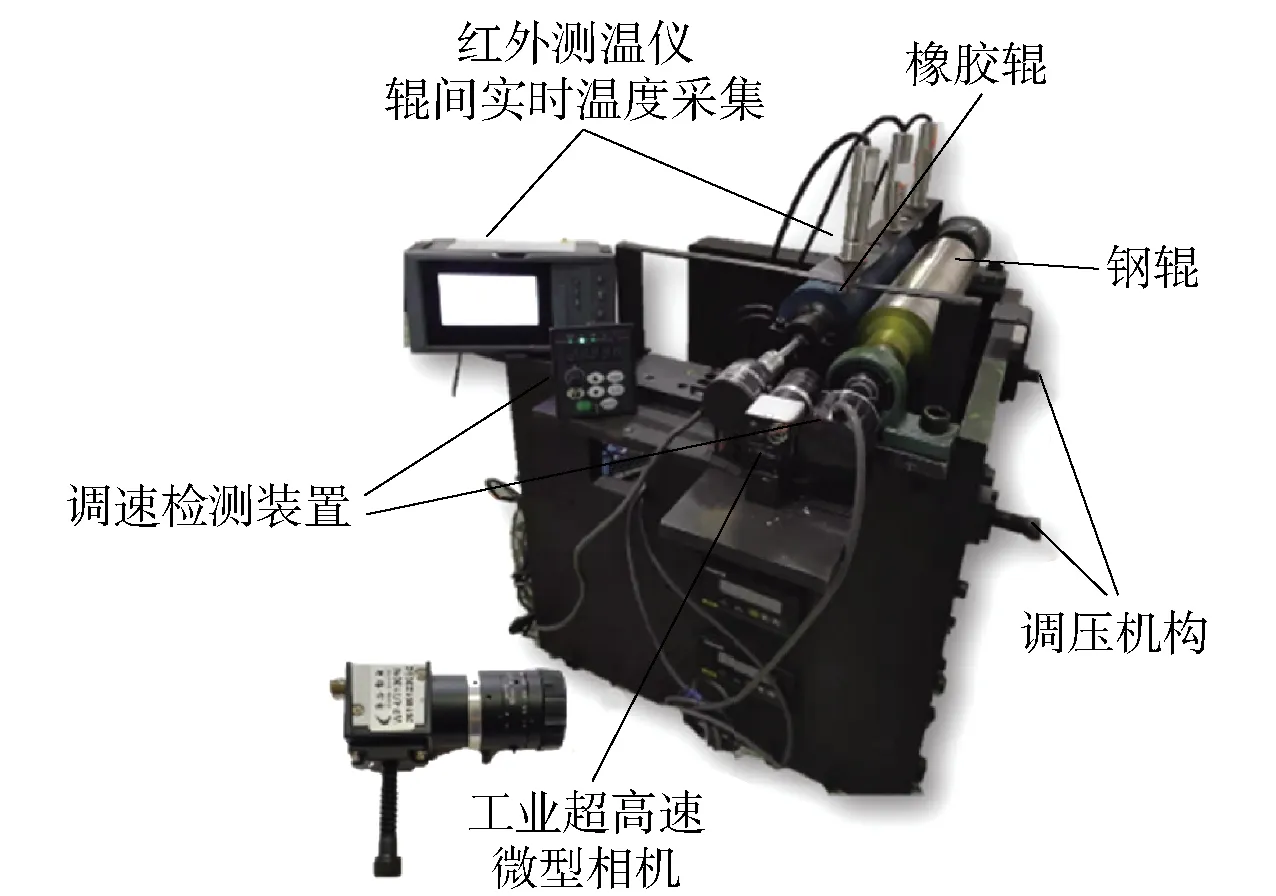
图1 钢- 橡胶对滚结构实验平台Fig.1 Experimental platform for steel-rubber rolling structure

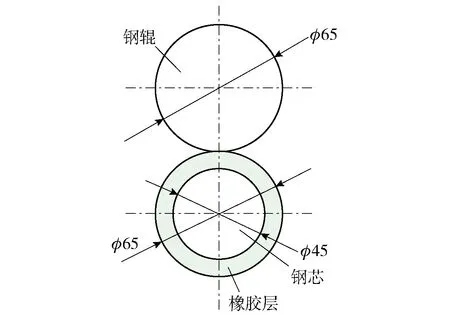
图2 钢- 橡胶对滚结构截面示意图Fig.2 Section diagram of steel-rubber rolling structure

实验工况设置为：辊间结合力为1 100 N；钢辊转速为180 r/min. 实验过程中同时启动实验台、工业高速微型相机与红外测温仪. 拍摄得到两辊接触状态，结合MATLAB图像处理功能，以橡胶层厚度为10 mm为基准，使用像素测距法获得橡胶辊的压深变形量与接触宽度. 图3、4分别为挤压旋转过程中橡胶辊的温度、压深变形量与接触宽度的变化情况. 由图3可以看出，橡胶辊温度随时间的增长而上升，计算每1 min橡胶温升量如表1所示，发现橡胶辊温升速率随时间增长先快后慢；图4中橡胶辊压深变形量与接触宽度随时间增长而变大，由于橡胶辊温升随时间变化是非线性的，故橡胶辊压深变形量及接触宽度随时间变化也是非线性的.

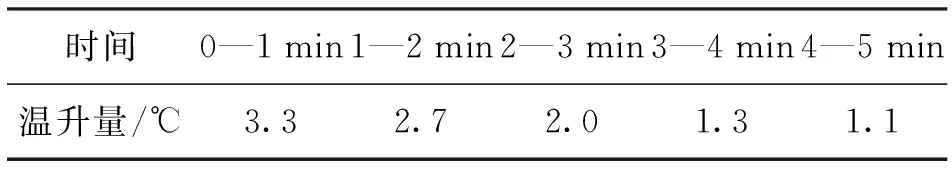
表1 每1 min温升量Table 1 Temperature rise per minute

图3 橡胶辊温度随时间变化情况Fig.3 Changes of rubber roller temperature with time

图4 橡胶辊压深变形量及接触宽度随时间变化情况Fig.4 Deformation and contact width change of rubber roller with time

2 不同温度下钢- 橡胶结构动力学仿真

由于钢- 橡胶辊动态力学特性实验无法测得橡胶的黏弹性程度以及von Mises应力应变、接触压力、接触刚度等动态力学特性，需进行不同温度下钢- 橡胶辊的动力学仿真.

2.1 橡胶材料模型的建立

首先需建立仿真中所用橡胶材料的模型. 本文所用到的钢- 橡胶存在显著的刚性差异，在两辊受辊间挤压力而动态转动过程中，橡胶辊变形主要发生在外覆橡胶层上. 橡胶高延展性、大变形特性与其超弹性有关，其应力- 应变本构关系呈高度非线性，故橡胶超弹性需要首先被考虑. 此外，对于常见的工业应用，如印刷、薄膜制造等领域，橡胶层表面不仅是关键成形区或流体通道，而且随着工况时间的累积或橡胶辊转速的增加，钢- 橡胶辊结构会出现显著的生热效应，这与橡胶黏弹性直接相关，因此橡胶黏弹性也需被考虑[10]. 为得到橡胶辊超弹、黏弹参数，需对橡胶材料进行动态热机械分析(dynamic-thermomechanical analysis,DMA)实验.

实验设备为德国GAOBA EPLECOR 500N动态热分析仪，采用与实验台橡胶辊材料相同的圆盘形试样(半径5 mm，厚度2 mm)，加载方式为剪切，对模型顶面施加周期循环的扭转位移载荷0.006 28sin(ωt) rad，底面施加固定约束，通过控制变量法改变温度或频率进行实验，分别进行以下实验：1) 时间扫描弛豫实验(20 ℃，8.5 Hz，0～100 s). 2) 温频扫描(20～50 ℃，1～60 Hz). 3) 温度扫描(20～50 ℃，8.5 Hz). 输出实验数据剪切松弛模量、剪切储能模量、剪切损耗模量、损耗因子和温移系数等[11]. 得到不同温度下橡胶材料应力松弛曲线如图5所示，图中反映了剪切松弛模量随时间的变化情况，可以看出温度的改变对橡胶材料剪切松弛模量有较大影响，各温度下橡胶材料达到平衡的时间有明显差异；橡胶材料损耗因子曲线如图6所示，损耗因子为应力应变相位差的正切，相同频率下温度的升高引起损耗因子的降低. 运用所得实验数据建立不同温度下的橡胶超弹- 黏弹复合本构模型.

图5 不同温度下的橡胶应力松弛曲线Fig.5 Stress relaxation curves of rubber at different temperatures

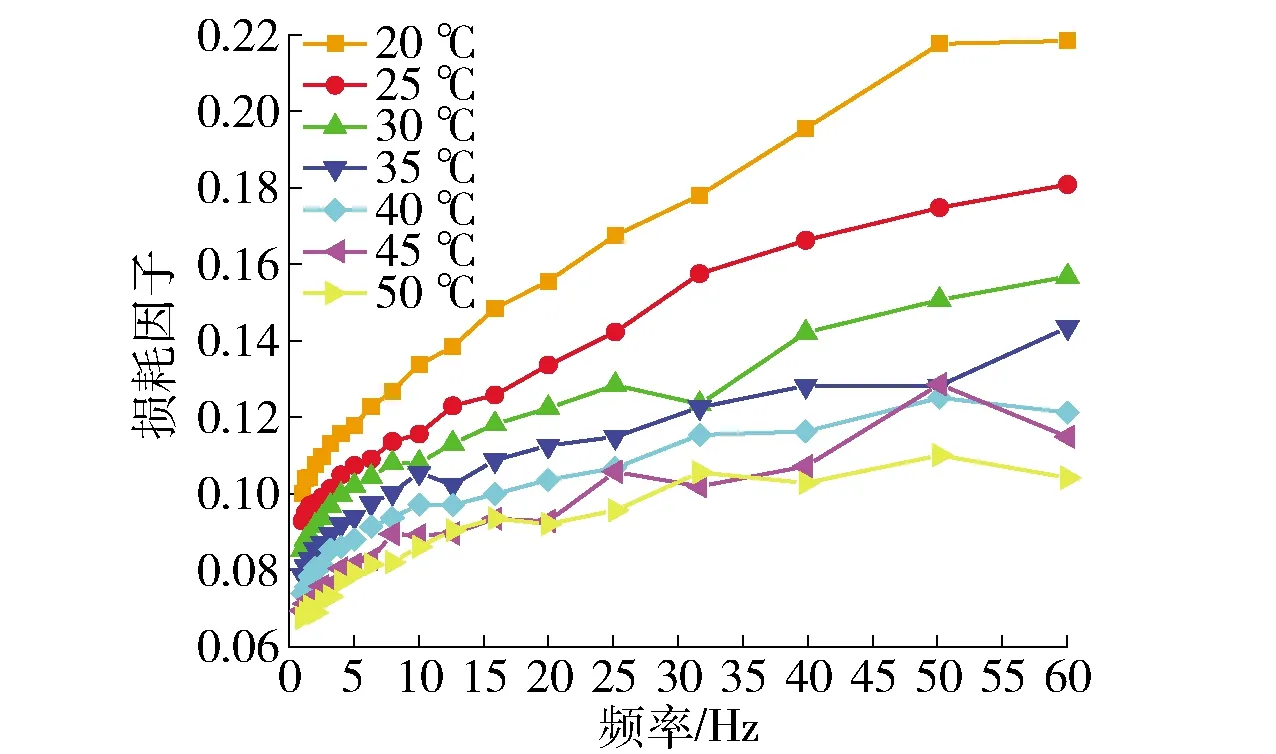
图6 不同温度、频率下的损耗因子Fig.6 Loss factors at different temperatures and frequencies

2.1.1 橡胶超弹性本构模型

多项式应变能函数

(1)

是描述超弹性材料的重要方法.如果取N=1，且只考虑i和j的第一项，则式(1)变为双参数Mooney-Rivlin超弹性本构模型，即本文所用的超弹性本构模型[11]：

(2)

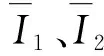
(3)

式(3)给出C10、C01和G、K之间的关系.G、K和μ分别是初始松弛模量、初始体积模量和泊松比.文献[12]讨论了不同的加载条件下C10/C01的比值关系，本文加载条件下关系式为C10=C01×10，结合DMA实验数据的初始剪切模量，所得橡胶材料的C10、C01和d值见表2.

表2 Mooney-Rivlin超弹性本构模型参数Table 2 Hyperelastic constitutive model parameters

2.1.2 橡胶黏弹性本构模型

黏弹性是橡胶最重要的特性之一，导致橡胶辊滚动接触过程中产生应力应变不同步从而引起能量耗散，能量损耗的大小影响了橡胶材料使用过程中的温度，进而影响材料的性能，因此需要考虑黏弹性的影响. 采用广义Maxwell黏弹性本构模型作为橡胶的黏弹性模型[13]，用离散Prony级数描述. 广义Maxwell模型的本构模型为

(4)

(5)

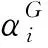
用Prony级数对DMA实验数据进行曲线拟合，获得橡胶的黏弹性参数如表3示.

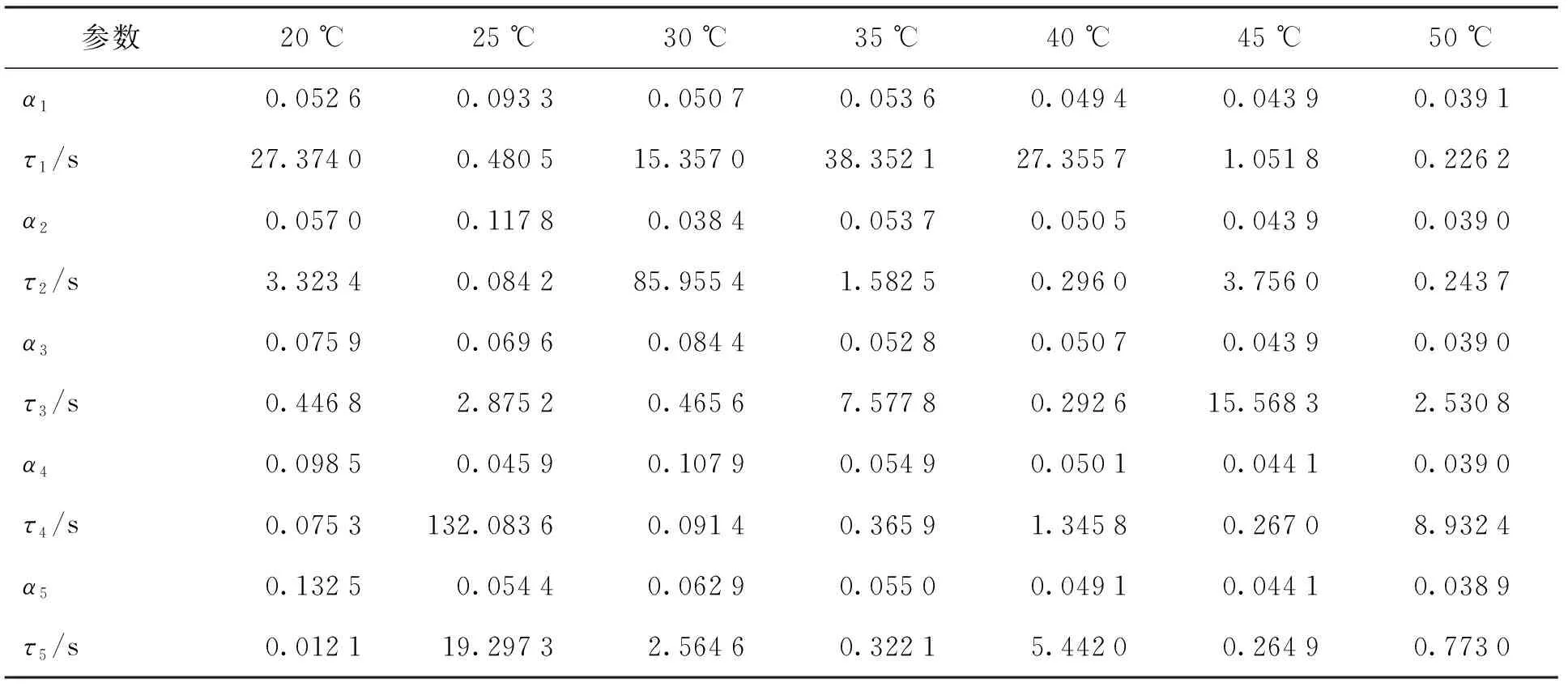
表3 黏弹性本构模型参数Table 3 Viscoelastic constitutive model parameters

最后，将超弹性参数与黏弹性参数叠加，建立了不同温度下的橡胶超弹- 黏弹本构模型. 将材料添加至ANSYS材料库中，通过参数拟合功能便可得到20～50 ℃区间内任一温度的橡胶材料参数.

2.2 仿真模型建立及工况设置

运用ANSYS WORKBENCH中的瞬态动力学模块对图2所示的挤压对滚钢- 橡胶结构进行不同温度下的动态力学仿真分析. 在实际工程构件中，应力应变是三维张量，本文所研究的辊系结构中，橡胶轴向长度远大于截面二维尺寸，轴向长度方向受均布载荷，符合“平面应变”假设，故对钢- 橡胶辊结构进行二维热结构场耦合分析，可有效减少耦合场仿真计算代价[14].

建立有限元模型如图7所示，模型上部为钢辊，下部为橡胶辊. 其中钢辊与橡胶辊钢芯材料弹性模量为2.06×105MPa,泊松比为0.3，密度为7 800 kg/m3. 橡胶材料通过第2.1节中描述的不同温度条件下超弹- 黏弹本构模型表征. 由于钢与橡胶刚性差异较大，将仿真中的钢辊和钢芯设置为刚体. 有限元网格尺寸设置为0.5 mm×0.5 mm以准确捕捉因为橡胶黏弹性引起的微小应变应力相位差.

图7 钢- 橡胶对滚结构二维有限元模型Fig.7 2-D finite element model of steel-rubber rolling structure

仿真工况设置与实验相同：辊间结合力为1 100 N，钢辊转速为180 r/min. 具体加载步骤如下：

1) 静态下压

设置钢辊第0—1 s完成下压；

2) 加速过程

钢辊在第1.0—1.2 s从0 r/min匀加速到180 r/min，并依靠摩擦带动橡胶辊转动；

3) 稳态运行

两辊以180 r/min速度稳定运行至2.2 s.

设置仿真环境温度为变量，温度范围为20～30 ℃(对应实验测得温度)，共进行6组不同温度条件下的动力学仿真，每组温度间隔2 ℃，设置两辊间摩擦因数为0.2.

3 结果与分析

3.1 橡胶辊黏弹性分析

在动态力加载下，橡胶材料的黏弹性特征表现为发生能量耗散，耗散的能量以热的形式散发出去.为分析温度对橡胶辊黏弹性的影响，需计算橡胶辊生热速率Q(单位时间单位体积下的能量耗散量)[15]，Q的表达式为

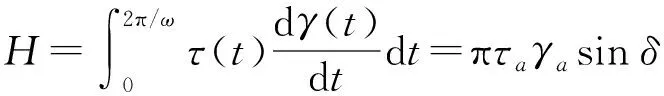
(6)

式中：H为单位体积下的能量耗散量，即滞后能密度；τa、γa分别为应力、应变幅值；ω为角频率；t为时间；δ是动态应力与动态应变之间的相位差；T为周期.

辊系设备挤压旋转过程中受力为单向力而非正弦力，表现为辊子处于周期性的“受力压缩”过程，Chu等[16]讨论了辊系设备运行中单一转动周期的受力问题，故橡胶辊实际生热速率为

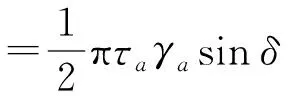
(7)

式中：H实、Q实分别为橡胶辊实际单位体积下的能量耗散量与生热速率；T实为橡胶辊单周期内经过挤压区的时间；b为接触宽度；R2为橡胶辊半径.

提取各温度两辊稳定运行状态下橡胶层表面任一节点(5588)任一周期的应力、应变幅值代入式(7)中计算，所得橡胶辊生热速率如表4所示. 随着温度的升高，橡胶辊的生热速率逐渐下降，黏弹性减弱，这是因为：1) 温度升高，引起橡胶辊应力幅值的减小(见3.3节)；2) 由DMA实验数据可知同频率下tanδ随温度升高而减小(见图6)，可推得应力应变相位差δ减小；3) 接触宽度的增大(见3.2节)引起橡胶辊经过挤压区时间变长；4) 应变幅值虽随温度升高而增大(见3.3节)，但相比于应力，数值要小很多，所以应变对能量耗散的影响相比应力较小.

表4 不同温度下橡胶辊生热速率Table 4 Heat generation rate of rubber roller at different temperatures

文献[17]中证明了橡胶材料黏弹性导致的滞后生热是辊系结构挤压旋转工况下橡胶辊的主要生热来源，在钢- 橡胶辊动态力学特性实验中，橡胶辊温升速率随温度增长逐渐变慢(见图3)，这是因为温度升高导致橡胶材料黏弹性减弱，生热速率下降.

3.2 压深变形量与接触宽度

在实际生产应用中，压深变形量与接触宽度均为橡胶辊在挤压旋转工况中动态力学的重要特性，是影响辊间介质传动稳定性与产品成型质量的关键因素. 将钢- 橡胶辊动态力学实验结果转化为温度与压深变形量、接触宽度的关系. 提取仿真中各温度下橡胶辊压深变形量、接触宽度并与实验结果对照，结果如表5、6所示.

表5 橡胶辊压深变形量Table 5 Deformation of rubber roller

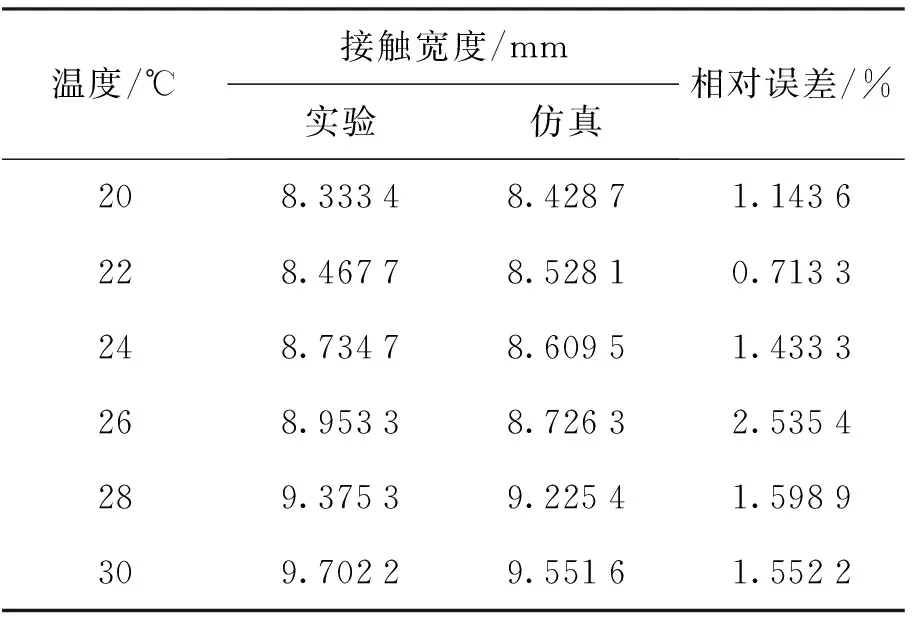
表6 橡胶辊接触宽度Table 6 Contact width of rubber roller

结果表明，随着温度升高，压深变形量与接触宽度均逐渐增大，仿真与实验所得趋势一致，且相对误差较小，证明了不同温度下动力学仿真的有效性与准确度. 当两辊进行挤压旋转工作时，从有限元的角度来讲，当一个节点进入挤压区，受力从而产生松弛现象，其模量会发生改变，该节点在挤压区的停留时间即为其松弛时间. 由于节点经过挤压区的时间远小于其转动一圈的时间，故该节点再次进入挤压区时，形变已经完全恢复，故橡胶辊在挤压旋转过程中均处于松弛的初始阶段. 由DMA实验获得的橡胶松弛曲线可知，温度的上升使橡胶材料初始松弛模量下降(见图8). 结合赫兹接触理论

图8 橡胶材料初始阶段松弛模量Fig.8 Relaxation modulus of rubber material at the initial stage

(8)

可知，辊间结合力相同条件下，接触宽度逐渐增大，仿真和实验结果一致.式中：b为接触宽度；F为两辊间结合力；υ1、υ2分别为钢辊、橡胶辊材料的泊松比；E1、E2分别为钢辊、橡胶辊弹性模量；R1、R2分别为钢辊、橡胶辊半径；L为辊长.由橡胶材料初始阶段松弛模量与温度的非线性关系以及式(8)可知，橡胶辊接触宽度随温度升高呈现非线性增长.

3.3 von Mises应力应变、接触压力与接触刚度

3.2节中证明了仿真的正确性，下面进一步讨论温度对钢- 橡胶辊结构动态力学特性的影响，选取von Mises应力、应变、接触压力与接触刚度4个关键动态力学参数进行研究.

1) von Mises应力、应变. 以20 ℃下瞬态动力学仿真为例，提取橡胶辊稳定运行状态下胶层von Mises应力、应变云图分别如图9、10所示，可以看出，由于钢辊与橡胶辊挤压旋转，橡胶辊胶层在接触区域产生形变，越靠近挤压区域应力越大，挤压区域应力最大，应变规律与应力一致.

图9 von Mises应力云图Fig.9 von Mises stress contour plot

图10 von Mises应变云图Fig.10 von Mises strain contour plot

取各温度橡胶辊稳定运行状态下的von Mises应力应变最大值如图11所示，当橡胶辊温度由20 ℃上升为30 ℃时，橡胶辊最大应力由0.494 7 MPa减小到0.481 9 MPa，最大应变由0.130 2增大到0.135 5. 随着温度的升高，von Mises应力最大值逐渐减小，von Mises应变最大值逐渐增大. 这是因为温度升高，橡胶材料本构模型发生改变，在橡胶辊所受挤压力不变时，导致其von Mises应力应变发生变化.

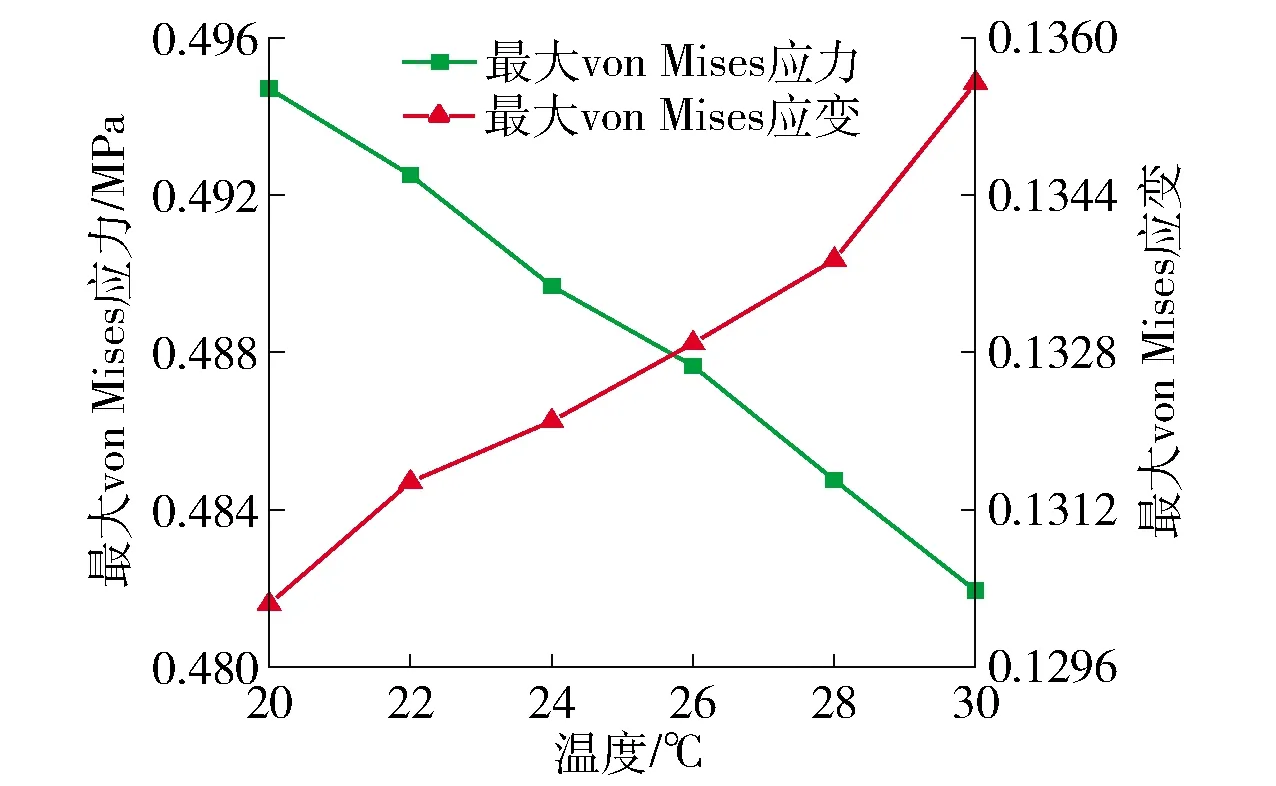
图11 不同温度下橡胶辊von Mises应力、应变最大值Fig.11 The maximum von Mises stress and strain of rubber roller at different temperatures

2) 接触压力与接触刚度. 接触压力是对滚结构最重要的动态力学特性之一. 如果接触压力稳定，两辊转动稳定性将得到加强. 例如在印刷机械中，它直接关系到油墨附着于印刷品的均匀程度. 接触刚度是橡胶辊在外力作用下，抵抗接触变形的能力，在实际生产中亦是不可忽视的重要因素. 不同温度下橡胶辊的接触压力与接触刚度最大值如图12所示.

图12 不同温度下接触压力与接触刚度最大值Fig.12 The maximum contact pressure and contact stiffness at different temperatures

随着温度的升高，橡胶辊接触压力与接触刚度均呈下降趋势，当橡胶辊温度由20 ℃上升为30 ℃时，橡胶辊最大接触压力由0.828 0 MPa减小到0.809 1 MPa，橡胶辊最大接触刚度由13.426 N/mm3减小到13.006 N/mm3，且与温度均呈现非线性关系. 这是因为温度升高导致接触宽度变大(如3.2节所示)，橡胶辊长度不变，辊间受载荷的面积增大，故橡胶辊接触压力下降；温度升高导致橡胶辊压深变形量增大，橡胶辊抵抗接触变形能力降低，接触刚度下降.

4 结论

本文以一对挤压对滚的钢- 橡胶辊结构为研究对象，通过理论、实验与仿真相结合的方法研究了不同温度下橡胶辊的黏弹性以及其动态力学特性，结论如下：

1) 对橡胶辊的黏弹性进行了研究，发现随着温度的升高，橡胶辊应力幅值、应力应变相位差减小，橡胶辊经过挤压区时间变长，导致橡胶辊单位时间的生热能力减弱，橡胶辊温升速率呈现出逐渐变慢的规律，即橡胶辊的黏弹性随温度的升高而减弱.

2) 通过钢- 橡胶结构动态力学特性实验与有限元仿真结合分析，发现2种方法中橡胶辊压深变形量与接触宽度均随温度的升高而增大，且二者相对误差较小，并结合赫兹接触理论，证明了仿真的准确性与可行性.

3) 通过钢- 橡胶对滚结构动力学仿真分析得出，橡胶辊最大von Mises应力值随温度的升高而减小，最大von Mises应变值随温度的升高而增大，且基本呈线性变化.

4) 橡胶辊最大接触压力及最大接触刚度随温度的升高而减小，这是因为温度的升高引起接触宽度的增大，导致橡胶辊在挤压对滚过程中接触面积增大以及抵抗接触变形能力降低，且由于接触宽度、压深变形量与温度之间的非线性关系，导致接触压力、接触刚度均随温度呈现非线性变化.