基于数据扩充的光伏组件故障诊断方法
尹春杰,宋彦螟,肖发达,隋 涛,李鹏飞,王亚男
(1.山东建筑大学 信息与电气工程学院,山东济南 250101;2.青岛供电公司,山东 青岛 266000)
0 引言
近年来,随着太阳能光伏发电技术的逐步成熟,其在全球范围内的应用规模也越来越大。据国际能源署2020年统计,中国太阳能光伏装机容量在2019 年底上升到30.1GW,与此同时,全球光伏发电总量也达到720TWh,并有望在2030 年增加到3 300TWh。光伏发电技术将成为继水力和风力发电技术之后的第三大可再生电力技术。光伏发电组件是整个光伏发电系统的核心部分,但其长年露天放置,运行环境恶劣,发生故障或性能降低的机率较高。因此,实现光伏组件性能参数的在线精确监测及故障诊断对于保证光伏发电系统的安全、高效运行至关重要[1-2]。
目前,光伏组件故障的传统诊断方法可分为在线诊断(红外图像法和多传感器法)与离线诊断(对地电容测量法和时域反射分析法)两种,但这些方法的应用都存在着各种限制条件。随着研究的不断深入,智能化诊断方法中的神经网络逐渐成为该领域的研究热点[3-4]。如文献[5-8]利用组件的各种参数进行故障研究;文献[9-13]将神经网络作为故障诊断的技术手段;文献[14-16]均涉及到白噪声扩充,但其应用白噪声的目的与本文将白噪声仅用于数据扩充的目的不同。本文通过比较组件参数的相关性,最终选定光伏组件的输出参数(输出电压、输出电流)与影响光伏发电组件的外界因素(太阳辐照度、表面温度)作为诊断依据,利用BP(Back Propagation)神经网络,提出基于数据扩充的光伏组件故障诊断方法,并引入原始数据与白噪声扩充后的数据进行诊断准确率与效率的对比分析,进而验证了该方法能够实现光伏组件故障的在线诊断。
1 光伏发电相关理论
1.1 光伏发电基本原理
如图1 所示,光伏发电实际上是电池内部P-N 结发生的反应,即太阳能通过该反应变换为电能。反应产生的空穴—电子对在电场影响及相互作用下将负载连接到电路后,两者可流入各自的极性区域并产生电流。

Fig.1 Schematic of photovoltaic cells图1 光伏电池原理
光电转换是一种复杂的非线性特征过程,图2 基于电池等效电路模型,从内部等效参数与外部电气特性两方面对光伏电池进行了简化描述[5-7]。

Fig.2 Photovoltaic cell equivalent circuit model图2 光伏电池等效电路模型
由以上电路模型,根据KCL 定律可得:

式中,I、U表示输出电流与电压,Iph表示光生电流,I0、A表示二极管的逆向饱和电流及理想因子,Rs、Rsh表示串、并联电阻值,T表示热力学温度,q=1.602×10-19C,K=1.381×10-23J/K。
光生电流Iph计算公式如下[6]:

式中,S表示太阳辐照度,T表示组件表面温度,SSTC、TSTC分别表示标况下的辐照度及温度,I0-STC表示标况下的反向饱和电流,ui表示电流温度系数。
组件短路时,U=0,二极管状态为不导通,I0可忽略不计,根据公式(1),可计算得到短路电流Isc:

组件开路时,I=0,此时二极管导通,忽略Rsh分支电流,可得开路电压Uoc[6]:

一般情况下,光伏组件在最大功率点处的输出电压Um与电流Im如下[7]:

可以看出,光伏组件发电功率除受自身材质等因素影响外,受辐照度及温度影响较大,可通过开路电压、短路电流及峰值功率点电压和电流等外特性参数予以表征[8]。
1.2 光伏发电组件典型故障
在实际运行环境中,光伏发电组件易发生多种类型故障,其中常见故障主要有短路、断路、异常老化、阴影遮挡等[2]。本文选取光伏组件故障中发生率最高的3 种故障类型,分别为光伏组件断路、阴影遮挡和局部阴影遮挡作为典型故障进行研究,以验证本文方法的有效性[9]。其中,断路故障通常是由生产缺陷或人为原因导致的;阴影遮挡故障是由光伏电站周围物体所造成的动态阴影遮挡,此类阴影故障面积较大,且会随着太阳位置的移动而不断变化,进而导致光伏组件出现热斑现象及功率下降等问题;局部阴影遮挡故障是由于小型物体(鸟粪、树叶)掉落在组件表面而引起的固定遮挡,此类故障需要运维人员通过清洁处理加以解决。
从内部或外部参数变化的角度分析,当光伏组件出现不正常情况时,参数会表现出不同的变化趋势。将这些参数更改视为故障诊断中的重要信息,则其故障诊断问题可类比于非线性问题。等效电路模型得出的超越方程无法直接求解,而BP 神经网络能够较好地解决此类问题,因此本文以BP 神经网络作为光伏组件的故障诊断工具。
2 光伏发电组件故障诊断模型设计
BP 算法于1986 年由Rvomelhart 和Mcclelland 首次提出[10]。其网络模型一般由输入层、隐含层以及输出层组成。
2.1 输入层
模型输入层节点数量选定为4 个,分别依据光伏组件本身的参数(电压、电流)和外界影响因素(辐照度、温度)对光伏组件状态进行判断,进而确定模型输入量分别为组件实时电压、实时电流、辐照度和表面温度[11-12]。
2.2 隐含层
1989 年,学者Nielson 通过理论分析,最终证明存在一个只有单个隐含层的BP 神经网络,在某些封闭区间的约束条件下,可无限接近任何连续函数,因此无需考虑隐含层层数问题[13]。以上即为万能逼近定理,故本文BP 神经网络模型确定为3 层。
隐含层节点数的选取就是对神经网络模型的优化过程。当选取节点数较少时,会导致网络无法正常学习;反之,当选取节点数太多时,将直接导致过拟合现象发生。由于在现阶段的理论中,尚未明确定义一种科学的方法来计算隐含层节点数,故节点数的选取原则为:满足模型精度要求,且节点数尽可能少[13]。
依据Kolmogorov 定理,通过公式(7)得出节点个数[4]:

式中,n、m分别表示一个输入和输出层的全部神经元个体数量,α取值范围为1~10。
经对多次实验结果的分析,选用α=8,以此选定隐含层单元数n1=12。隐含层通常选用tansig 或logsig 函数,以满足输入为任意取值,并且二者区别在于logsig 输出值在0~1 之间,为单极性;tansig 输出值在-1~+1 之间,为双极性,也称为双曲正切函数。本文为满足网络输出的要求,选定隐含层为tansig函数,其函数公式如式(8)、图像见图3所示。
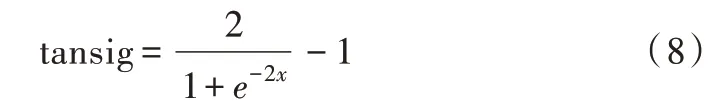

Fig.3 Tansig function graph图3 Tansig 函数图
神经网络隐含层输出为[6]:
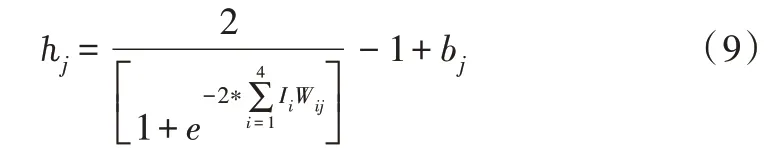
式中,Ii表示网络输入量,Wij表示隐含层之前的网络权值,bj表示网络对应阈值,j取值范围为1~12。
2.3 输出层
神经网络模型输出层节点数量选定为8 个,用于区别组件的8 种运行状态,即运行正常、组件断路、阴影遮挡、局部遮挡、组件断路与局部遮挡、组件断路与阴影遮挡、阴影遮挡与局部遮挡、组件断路与阴影遮挡及局部遮挡。故障状态类型定义如表1 所示。

Table 1 Types of fault status表1 故障状态类型
为满足神经网络的输出为任意值,由隐含层所选函数确定输出层函数。purelin 函数图像如图4 所示。
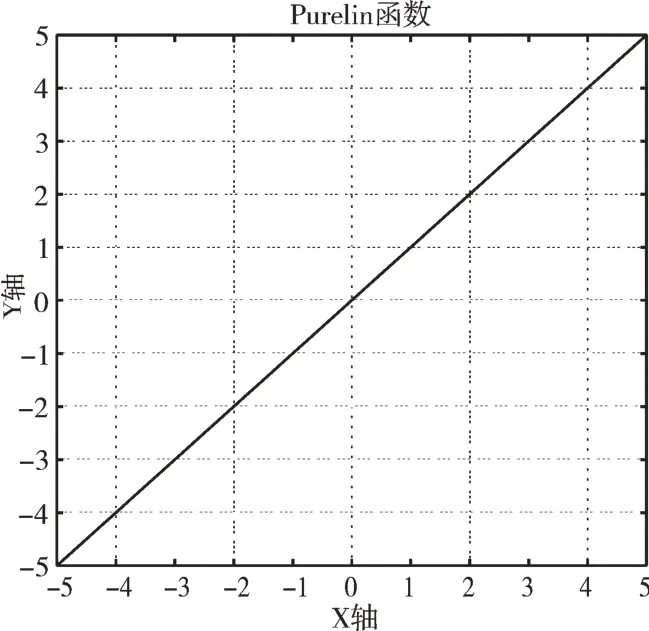
Fig.4 Purelin function graph图4 Purelin 函数图
综上,本文BP 神经网络诊断模型架构如图5 所示。

Fig.5 Model structure图5 模型架构
图中,Wij表示从输入层到隐含层的连接权值;Wjk表示从隐含层到输出层的连接权值,其中,i=4,j=12,k=8;hj表示隐含层输出。
模型建立后,神经网络输出层输出为[6]:

式中,Sk表示网络输出值,hj、Wjk如图5 所示。
从实验仿真结果可以看出,无论是正弦叠加的信号、含有高斯噪声的信号,还是形态有明显差别的信号,此方法都可以很好地进行信号的分解。信号分量的整体趋势不会发生变化,通过希尔伯特变换,可以计算出符合信号原始特征的瞬时频率等参数。
3 故障诊断实验及结果分析
3.1 数据样本获取及处理
样本数据获取是BP 神经网络故障诊断模型能否成功的关键,而故障诊断模型成功与否的评定标准则是模型诊断结果的准确性[14]。理论上,样本数目越多,训练后故障诊断模型的诊断结果越准确。但在现实环境中,往往很难获得样本数据,已知故障类型数据的获取更是神经网络故障诊断的难点[2]。因此,本文在小样本数据的基础上,提出利用白噪声进行原始小样本数据的扩充,以获取大量训练样本[15-16]。
3.1.1 原始数据
本文样本数据选用文献[9]中的实测故障数据(电压、电流、辐照度、温度),经过相应处理后,将其作为模型训练样本与验证样本。组件可能的故障状态为8 种,每种状态有8 组数据,共得到64 组样本数据。
3.1.2 白噪声扩充原始数据
热噪声即为白噪声,因为在可见光谱中,白光谱也是均匀分布的,并且热噪声谱与白光谱相似。除热噪声的统计特性外,在正常情况下,其还遵循高斯分布,因而又得名高斯白噪声。
由于原始训练样本数量太少,依据白噪声扩充数据的一般性规律,可对样本添加1%~10%的白噪声。设原始信号为X={U,I,S,T},要向该信号中加入百分比为β 的高斯白噪声,可借助于MATLAB 中的AWGN 函数向信号X中添加噪声[17]。具体实现步骤如下:
(1)求出噪声的方差D(X)。噪声方差求解方程如下:

式中,β为要添加的噪声百分比,RMS(X)为信号X的相对均方差。

式中,X为原始信号,D(X)为噪声方差,Y为加入白噪声后的信号。
本文在样本中添加β=2%的白噪声进行数据扩充,进而得到384 组数据,将其用于训练神经网络权值与偏差。图6 即为在原始小样本数据中添加2%白噪声后的数据对比分析图。

Fig.6 Comparison of two data sources图6 两种数据源对比
由图6 分析可知,利用白噪声进行数据扩充,其拟合数据源均在原始数据曲线附近波动,偏差不明显,因此扩充后的数据可视为有效扩充。
3.2 实验结果及分析
光伏发电组件故障诊断方法的有效性验证是建立在BP 神经网络训练完成的基础上,利用验证样本对网络期望输出与实际输出结果作比较,以此判断模型性能。
3.2.1 基于原始数据的诊断模型结果分析
已知获取的原始数据为64 组(8 种故障状态各自包含8 组数据),可视为小样本数据。任意抽取其中的48 组数据用于训练,其余数据作为验证样本,用于评价诊断模型的性能指标。其部分验证样本与期望输出以及网络实际输出结果如表2、表3 所示。
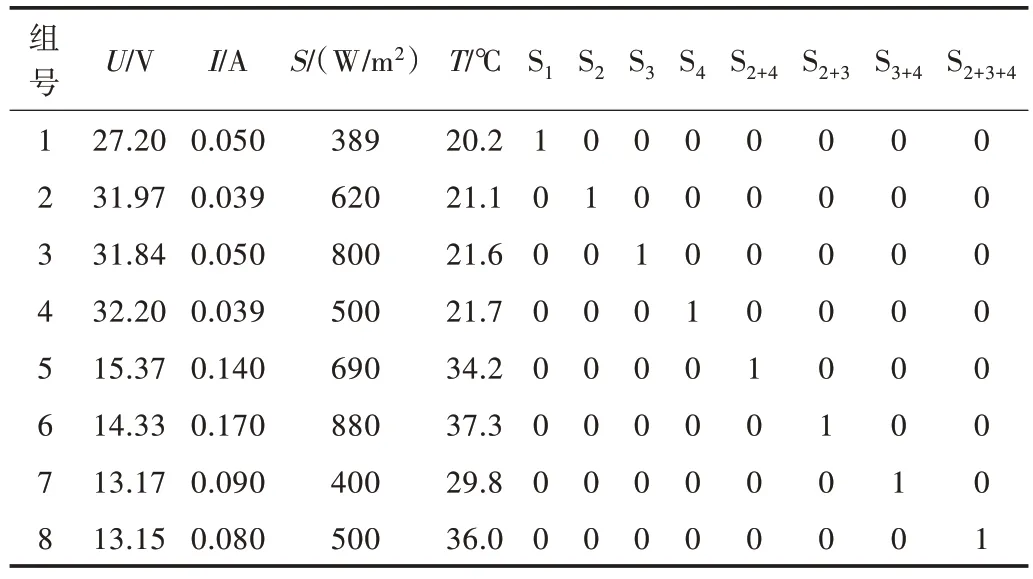
Table 2 Part of the verification sample and expected output表2 部分验证样本及期望输出
在MATLAB 平台上训练BP 神经网络,在已知特定故障状态类型下,输出层的输出值应等于1 或无限接近于1,而不属于其故障状态的输出值应等于0 或无限接近于0[9]。在表3 中,显然第2 组样本的诊断结果不正确,即本次诊断结果的准确率为93.75%,网络实际输出不完全符合期望输出的定义。BP 神经网络模型在小样本数据条件下进行多次实验,准确率分别为87.5%、81.25%、75%等。多次实验的平均准确率在81.25%以上,每次诊断结果的输出均不相同,且准确率无法达到100%,因此将小样本数据应用于该模型存在些许不足。

Table 3 Actual output results of the network表3 网络实际输出结果
经过对故障诊断模型的整体分析及不同实验的验证,确定模型设计完全正确,同时排除可能的影响因素,最终判断上述模型诊断结果存在不足的原因为样本数量太少,网络缺乏有效训练。故下文利用白噪声进行原始数据扩充,获取大量训练样本以验证模型的正确性与有效性。
3.2.2 基于扩充数据的诊断模型结果分析
在利用白噪声进行原始数据扩充后,总计得到384 组样本数据。任意选择其中80%的数据作为训练样本,余下20%的数据作为验证样本。部分验证样本与期望输出以及网络实际输出结果如表4、表5 所示。
由表4、表5 分析可知,表5 中的网络实际输出结果完全符合期望输出的定义,诊断模型稳定性较好,即BP 神经网络模型多次诊断结果均完全正确,准确率为100%。

Table 4 Part of the verification sample and expected output表4 部分验证样本与期望输出
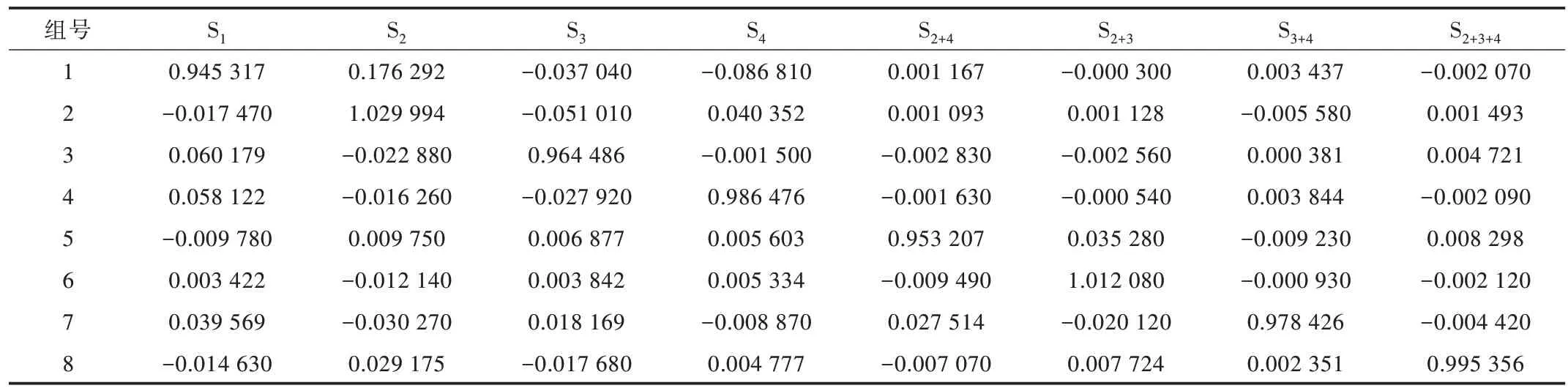
Table 5 Actual output results of the network表5 网络实际输出结果
3.2.3 诊断结果分析
根据上述两种数据源进行故障诊断结果对比,如表6所示。
由表6 的分析可知,两种方法的准确率相差较为明显,但所花费时间差别不大。BP 诊断模型整体所用时间较短,其诊断效率可满足光伏组件的故障诊断要求。其准确率差异则是因数据源不同导致的,即原始数据因样本数量太少,导致网络诊断结果不稳定且准确率不高。经白噪声扩充后的数据量可满足实验要求,网络诊断结果稳定且完全正确。综上所述,本文提出的光伏发电组件在线故障诊断方法是可行且有效的。

Table 6 Comparison of diagnosis results表6 诊断结果对比
4 结语
本文研究光伏发电组件故障诊断问题,利用同一个故障诊断模型,采用两种不同数据源分别对其诊断准确率和效率进行了对比分析。结果表明,采用白噪声扩充后的数据源,模型能够稳定、准确地判断光伏组件故障类型。同时清楚认识到小样本数据在故障诊断中的不足之处,加深了对于白噪声扩充小样本数据手段的理解,为进一步验证本文基于数据扩充的光伏组件故障诊断方法的可行性及有效性提供了理论依据。在某种程度上,也可有效节省光伏组件实际故障排查所需的人力、物力与财力等。

