三自由度拟人并联机构的尺度参数优化研究*
罗怡沁,吕兴荣
(浙江纺织服装职业技术学院 机电与轨道交通学院,浙江 宁波 315211)
0 引 言
机器人技术的快速发展,使得机械臂在工业、医疗、航空航天等领域得到了广泛的应用。
由于串联机构具有控制简单、运动灵活、工作空间大等优点,目前的机械臂多采用串联机构[1]。但串联机构运动惯性大、结构易震动等缺点又导致机械臂的动态精度较低。由于拟人机械臂要完成一系列仿人操作,应具有结构稳定、承载能力强等特点,而并联机构正好能满足这样的要求。除此以外,并联机构[2,3]还具有刚度大、运动惯性小、精度高等众多优势。
对并联机构进行尺寸参数优化时,需要确定优化的目标函数,即机构性能指标。通常,并联机构的性能评价包括运动学与动力学指标,其中动力学分析较为复杂。利用达朗贝尔原理可将动力学能够转换为静力学问题,因此,分析机构的运动学与静力学指标可实现综合性能优化。一般可采用雅克比矩阵法[4,5]和影响系数法[6]分析运动学指标,并定义传递性能[7-9]、各向同性[10,11]、全域性能[12]、局部评价指标[13]等性能。
基于尺寸参数与性能指标之间的映射关系,筛选出影响机构性能指标的结构参数,并对其进行优化,可提高机构综合性能。张虎等人[14]运用BP网络算法与遗传算法,以工作空间和全局条件指标为目标函数,经综合优化得到了3-DOF并联机床较优的尺寸参数。李超等人[15]将目标工作空间内最差性能指标作为优化对象,对球面并联机构结构参数进行了优化,可避免机构在某些姿态下出现病态雅克比矩阵的情况。李树平等人[16]以雅可比矩阵条件数最大值定义最差灵巧度,使用差分进化算法,确定了合理的球面并联机构结构参数。金振林等人[17]针对一种2-DOF并联行程放大机构,基于机构运动灵活性能评价指标,采用容限加权法确定了一组合理的结构参数。
上述方法均以运动学方面的性能指标作为目标来优化尺寸参数,并未考虑受力时机构对机构性能的影响,因此存在因机构受力或力矩过大,从而导致机构杆件变形甚至断裂的问题。
针对肘、腕关节,笔者提出一种新型并联三自由度拟人机械臂;首行分析机构的自由度,建立位置反解方程,并绘制位置工作空间轮廓图;定义速度与力传递、各向同性性能评价指标,给出全域性能图谱;在此基础上,建立多目标优化模型,采用加权求和法定义目标函数的权值系数,结合空间模型技术得到合理的结构尺寸参数。
1 运动学分析
由人体解剖学可知[18,19],人臂的骨相当于机械臂的刚性杆件,若干杆件配合组成机构钢架,关节则相当于铰接点;肘关节可完成一组伸展-超伸-屈曲运动,其自由度为1;腕关节可完成一组背屈-掌屈垂直运动和一组桡屈-尺屈水平运动,其自由度为2。
根据人体关节运动特点,本文提出一种2PUS-PRRRS(P:移动副,U:虎克铰副,S:球副,R:旋转副)三自由度并联机构,其简图如图1所示。

图1 拟人机械臂的机构简图
图1中,笔者建立静坐标系{R}:O1-X1Y1Z1,Y1轴与O1F平行,Z1轴与HO1平行,X1轴由右手定则确定;动坐标系{S}:O2-X2Y2Z2,Y2轴垂直平面ABO2,Z2轴平行平面ABO2并过AB中点,X2轴由右手定则确定;
P1、P2和P3表示肘关节机构的3个直线移动副,移动副之间互相平行,且均固定在机构左端。初始位姿时,机构各个移动副的输入恒等于零,杆FO2分别与面ABO2垂直。
1.1 基于螺旋理论的自由度分析
该并联机构(拟人机械臂)具有2个相同分支PUS与一个单支PRRRS。本文建立PUS分支的运动螺旋,如图2所示。

图2 并联机构PUS分支的运动螺旋图
在初始形位下,PUS分支的运动螺旋系为:
(1)
对分支PUS的运动螺旋进行互易积,可得反螺旋系:
(2)
式(2)表明,在初始形位下,PUS分支对动平台没有约束力和约束力偶。
采用相同构图法,可得PRRRS分支的运动螺旋。由于杆FO1与静平台固连,此处将该分支拆为两个部分,如图3所示。
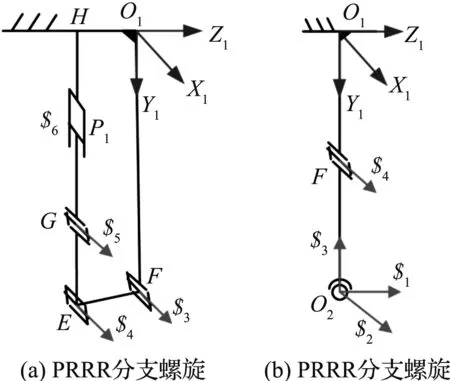
图3 并联机构PRRRS分支的运动螺旋图
在初始形位下,图3(a)中机构的运动螺旋系为:
(3)
对PRRR分支求反螺旋,可得反螺旋系:
(4)
该机构为串联机构,根据Bennett机构自由度计算方法,空间不相交的3条直线必不相关,因此,其运动螺旋系的最大线性无关数为3。
运动螺旋的反螺旋数为3,公共约束为3,阶数为3,机构不存在冗余约束,因此,PRRR机构的自由度为:

(5)
由式(5)知,该串联单环机构只有1个自由度,即绕X轴转动方向的自由度,且作用为辅助图3右侧支链的运动。
在初始形位下,图3(b)中的机构运动螺旋系为:
(6)
对RS分支求反螺旋,可得反螺旋系:
(7)
式(7)表明,在初始形位下,RS分支对动平台施加一个沿X轴和Y轴方向的约束力。
由式(2,7)可知,该机构不存在公共约束,即λ=0,因此,该机构的阶数为:
d=6-λ=6
(8)
除去公共螺旋约束,剩余的约束螺旋数t=2,构成一个k(k=2)系的螺旋,由此,可得肘、腕关节机构的冗余约束为:
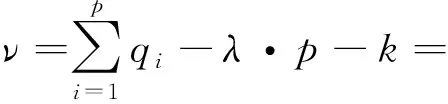
(9)
可见,机构的3个球铰存在1个绕Z轴旋转局部自由度,故ξ=1。
机构的自由度为:

(10)
由机械臂的反螺旋和局部自由度可知:机构的约束为沿X、Y方向的移动和绕Y轴的转动,即机构能沿Z轴方向移动和绕X、Z轴转动。
通过分析机构运动可知:3条分支各个运动副的轴线都与初始位姿时动坐标系的X轴或Z轴平行,轴线仅发生位置变化,未改变方向。因此,该并联机构具有全周自由度,运动性能好,在非奇异位形下,能连续平稳地进行两转一移运动。
1.2 位置反解
参考点O2在{S}坐标系中的位置为(0,0,0)T;设参考点O2在{R}坐标系中的位置坐标为(0,y,z)T,姿态为(α,0,γ)T;杆EF与杆FO2的夹角θ为常量,杆FO1长度为n;M、N点关于{R}坐标系的Z1轴对称分布,杆EF的长度为k,θ1为杆FO2绕F点的转角。由三角函数可得:
(11)
在动坐标系{S}中,A、B点关于{S}坐标系的Z2轴对称分布,A、B点的位置矢量为:
(12)

(13)
式中:ci=cosi;si=sini;i=α,β,γ。
A、B两点在静坐标系{R}中的位置矢量为:
(14)
通过结构几何关系,可得4杆FO2、AD、BC和EG的方程式:
(15)
综合式(14,15),可得肘、腕关节位置反解的表达式:
(16)
其中:
1.3 工作空间分析
设ψ1、ψ2和ψ3分别为杆FO1与O2F、DM与AD、CN与BC之间的夹角;ψ1max、ψ2max、ψ3max与ψ1min、ψ2min、ψ3min分别表示ψ1、ψ2和ψ3的最大值和最小值,肘、腕关节的转动副约束条件为:
(17)
设Limax和Limin(i=1,2,3)分别为3个直线移动副P1、P2和P3的输入位移的最大值和最小值,则肘、腕关节的驱动器约束条件为:
Limin≤Li≤Limax
(18)
为直观地展示机械臂的工作空间,此处假设各参数值为:h=150 mm,m=300 mm,a=150 mm,e=440 mm,d=440 mm,b=300 mm,f=260 mm,c=235 mm,n=440 mm,k=175 mm,L10=200 mm,L20=300 mm,L30=300 mm。
采用坐标搜索法[20]可得到肘、腕关节机构的三维位置工作空间形状图,如图4所示(视图2通过视图1绕θ1轴逆时针旋转90°而得)。

(a)视图1

(b)视图2
2 运动学性能分析
2.1 速度雅克比的求解
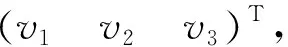
(19)
式中:φ1—杆EG绕G点的转角。
Δl1关于时间的导数为v1,θ1关于时间的导数为ω1;通过化简可得ω1的解析表达式,即杆FO2绕F点转动的角速度为:
(20)
机构参考点O2的线速度矢量为:
VO2=(VYVZ)=s1dω1
(21)
设机构的A和B点相对于静坐标系{R}的线速度矢量分别为VA和VB,可得表达式:
(22)
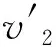
(23)

(24)
经转化,可得矩阵方程:
(25)

可推出关于ω的表达式为:
ω=Jωv
(26)
其中:ω=(ωXωZ)T。
由于VO2仅受角速度ω1的影响,综合上式可得关于角速度ω1与ω的表达式为:
(27)
式中:J∈R3×3—肘、腕关节机构的速度雅克比矩阵。
矩阵J的具体表达式为:
(28)
考虑到线、角速度属于不同量纲,当机构不在奇异位形时,上式可改写为:
(29)
式中:JV—线速度雅克比矩阵;Jω—角速度雅克比矩阵。
同样地,可得静力学雅克比矩阵为:
G=(J-1)T
(30)
2.2 运动学性能评价指标与分布图
2.2.1 角速度传递性能评价指标
当机构不在奇异位形时,Jω可分解出奇异值,存在正交矩阵Cω∈R2×2、Dω∈R3×3,使:
(31)
其中:
在矩阵Λω中,元素δ1ω和δ2ω为Jω的两个奇异值,设两元素的关系为δ1ω≤δ2ω。当机构不在奇异位形时,若输入向量v是单位向量:
vTv=1
(32)
综合式(31,32),可得到奇异值δ1ω、δ2ω的方程表达式:
(33)
通过定义线速度传递性能评价指标KL和角速度传递性能评价指标KA,可得到机构的运动性能在工作空间内的分布情况。定义KL和KA为:
(34)
角速度性能评价指标表征机构驱动到动平台的运动映射关系,其值越大,说明机构的速度传递性能越好。
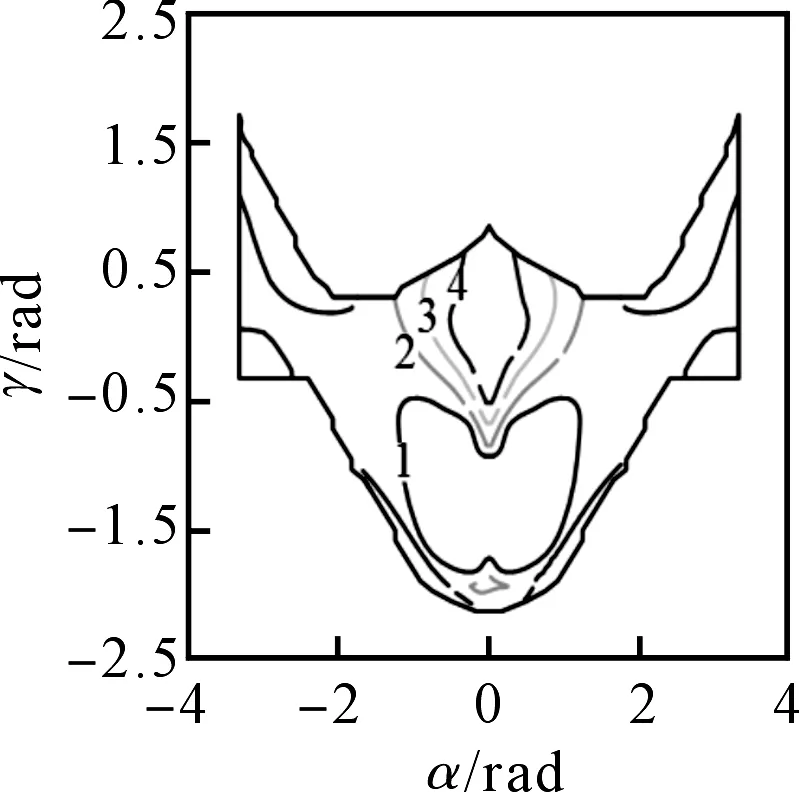
笔者利用MATLAB绘制角速度传递性能评价指标KA在工作空间内的分布图,如图5所示。
(a)θ1=0 rad (b)θ1=π/6 rad

(c)θ1=π/3 rad
由图5可知:(1)角速度传递性能评价指标在工作空间内的波动小,等高线分布较有规律性;(2)等高线均以α轴对称轴分布,且在α轴位置处数值较大,说明机构在对称轴位置的运动学性能较好;(3)在工作空间内,指标数值不存在等于0的情况,表明机械臂的全域传递性能较好;(4)随着自变量θ1的改变,指标数值变化不大,说明机构末端执行器的映射区间较稳定。
同样地,定义力传递性能评价指标KF和力矩传递性能评价指标KM,可得到机构在工作空间内的力学性能分布情况。
2.2.2 角速度各向同性性能评价指标
定义机构在输入速度矢量v为单位向量时,末端输出速度的最大值ηkmax和最小值ηkmin,可得到机构运动性能在工作空间内的分布情况。
此处给出角速度各向同性性能评价指标为:
Kη=ηkmin/ηkmax
(35)
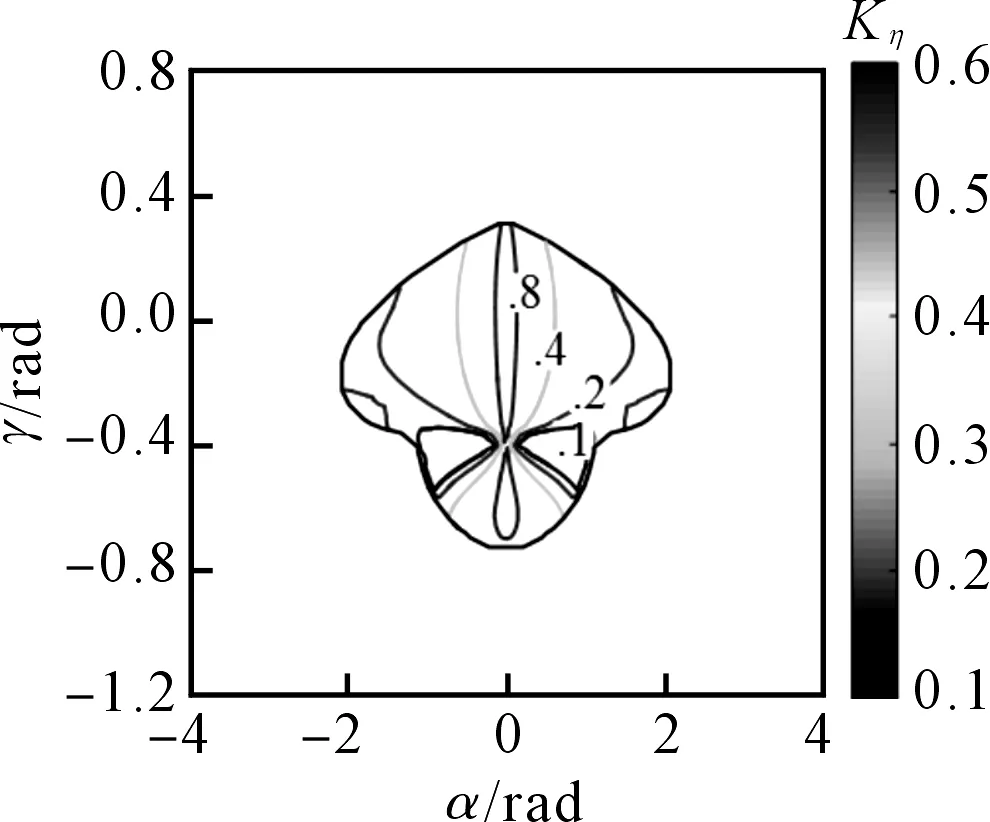
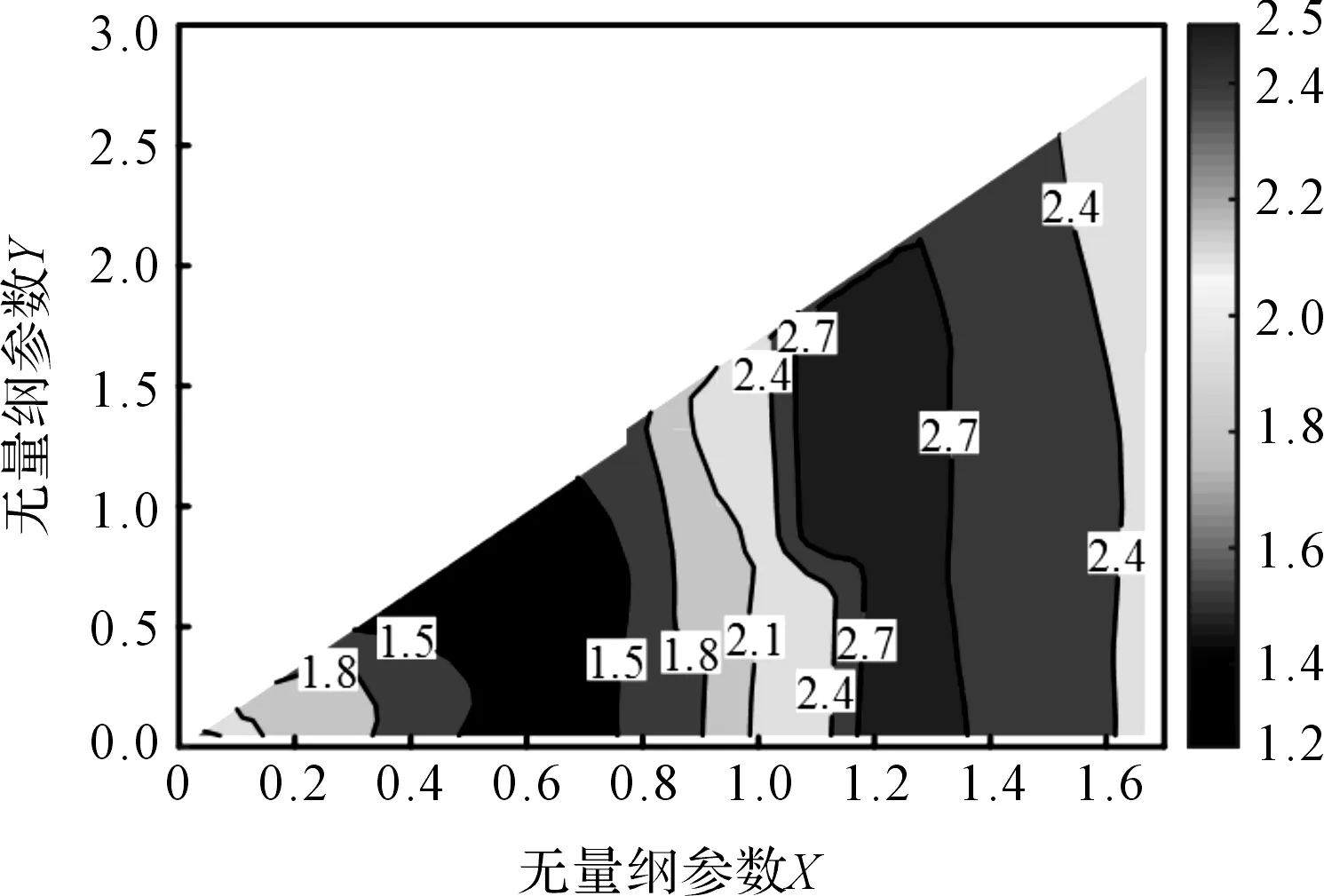
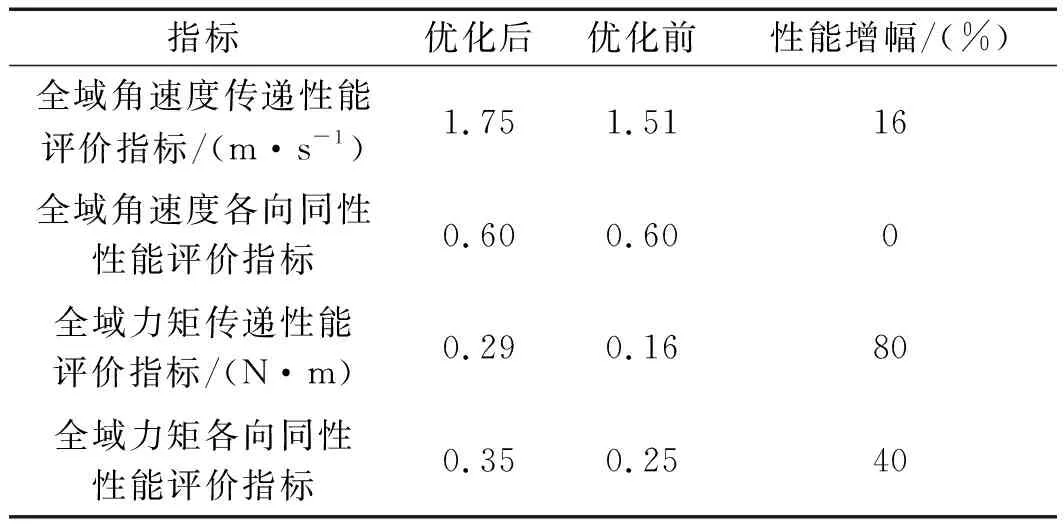
其中:0 笔者利用MATLAB绘制角速度各向同性性能评价指标Kkη在工作空间内的分布图,如图6所示。 (a)θ1=0 rad (b)θ1=π/3 rad (c)θ1=π/6 rad 由图6可知:(1)角速度各向同性性能评价指标在工作空间内的波动小,等高线分布较有规律性;(2)等高线均以α轴为对称轴分布,且在α轴位置数值更接近于1,说明机构在对称轴位置的运动学各向同性性能较好;(3)随θ1的增大,机构的角速度各向同性性能逐渐变差。 基于拟人特征,机构各关节均以人臂作为参照,且遵循一定尺度与比例。当机构的某部分尺数均被定义时,其他部分可通过比例系数确定;另一方面,根据各项指标与机构参数的映射关系,笔者选定m、a和b作为机构的设计参数。 笔者利用空间模型技术将参数无量纲化[21],即: (36) (37) (38) 综合上式,笔者绘制上臂无量纲参数的空间模型图,如图7所示。 图7 上臂无量纲参数的空间模型图 为了便于分析,笔者将上臂无量纲参数空间模型的三维xyz转为二维的xy坐标,即: (39) 根据转换关系,笔者绘制上臂参数的平面映射图,如图8所示。 图8 上臂参数的平面映射图 图8中,平面P′Q′S′为肘、腕关节机构上臂参数构建的几何空间模型形状。 以上述运动学性能评价指标为局部评价空间,无法全面评价机构的运动学性能。因此,本文定义全域线速度传递性能评价指标ζ(L)、全域角速度传递性能评价指标ζ(A)和全域角速度各向同性性能评价指标ζ(Kη),分别表示线和角速度传递性能、角速度各向同性性能在整个机构工作空间内的平均值。 其中,全域线速度传递性能评价指标ζ(L)为: (40) 全域角速度传递性能评价指标ζ(A)为: (41) 全域角速度各向同性性能评价指标ζ(Kη)为: (42) 机构的全域运动学性能图谱如图9所示 (a)ζ(L)/(m·s-1) (b)ζ(A)/(rad·s-1) (c)ζ(Kη) 由图9可得:(1)全域线速度传递性能评价指标随参数增大,数值变化坡度小;(2)全域角速度传递、各向同性性能评价指标随参数增大,数值变化大,等高线垂直落差大;(3)机构上臂的3个参数m、a和b对全域线速度传递性能评价指标影响不大,对全域角速度传递、各向同性性能评价指标影响较大。 同样地,本文定义全域力传递性能评价指标ζ(F)、全域力矩传递性能评价指标ζ(M)和全域力矩各向同性性能评价指标ζ(Sη),分别表示力和力矩传递性能、力矩各向同性性能在整个机构工作空间内的平均值。 其中,全域力传递性能评价指标ζ(F)为: (43) 全域力矩传递性能评价指标ζ(M)为: (44) 全域力矩各向同性性能评价指标ζ(Sη)为: (45) 笔者绘制了全域静力学性能图谱,由该图谱可知:机构上臂的3个参数m、a和b对全域力传递性能评价指标影响不大,对全域力矩传递、各向同性性能评价指标影响较大。 由于全域线速度、力传递性能评价指标受参数影响不大,此处以全域角速度传递性能评价指标ζ(A)、全域角速度各向同性性能评价指标ζ(Kη)、全域力矩传递性能评价指标ζ(M)和全域力矩各向同性性能评价指标ζ(Sη)作为机构的优化目标;并采用归一加权求和法,将各优化目标函数权值定义为相同数值,以避免每个优化指标的权重不同。 由性能图谱可得到的各指标最大值ϑmax和最小值ϑmin,无量纲化参数可表示为: (46) 式中:ϑ(x)—参数变化范围内所有的指标值;Fi—无量纲化的目标函数。 目标函数Fi是在参数变化范围内各个指标所占的比值,可保证各优化指标相对目标函数而言同等重要。笔者建立多目标函数如下: (47) 在无量纲参数的XY坐标范围区间内,笔者在X轴均匀取点,设定步长为0.1,得到相应范围内的Y值。 在工作空间内搜索得到机构的综合性能优化结果,如图10所示。 图10 综合性能优化结果图 由图10可知:上臂无量纲参数在X轴上的数值在1.2~1.3之间,且Y轴上的数值在0.8~1.7之间的区域内,机构的综合性能最优[22]。 笔者取X=1.2,Y=1.2作为最优值,计算参数优化前后的性能指标,如表1所示。 表1 参数优化前后的性能指标对比表 由表1可知:经优化后,全域角的速度传递性能、力矩的传递性能和各向同性性能分别提高了16%、80%、40%。 在其他7个参数不变的情况下,笔者选取一组各项性能指标均佳的结构尺寸参数为:m=270 mm,a=100 mm,b=260 mm。 针对并联机构运动学与静力学综合性能的优化问题,本文提出了一种多尺度参数优化方法;首先在分析机构自由度基础上建立了位置反解方程,绘制了机构三维位置工作空间轮廓图;然后定义了机构的角速度和力的传递、各向同性性能指标,绘制了各指标在工作空间内的分布图,确定了待优化的机构参数,建立了多目标函数方程,得到了合理的结构尺寸参数;最后结合空间模型技术和归一加权求和法,对2-PUS/PRRRS机构的参数进行了优化,并通过数值仿真方法对其进行了验证。 研究结果表明: (1)2-PUS/PRRRS并联机构具有两转一移自由度,符合人体肘腕关节的运动特性,可实现肘关节的伸展-超伸-屈曲运动以及腕关节的背屈-掌屈垂直运动和桡屈-尺屈水平运动; (2)2-PUS/PRRRS机构不同类型的结构参数对其性能影响程度不同,其中驱动器之间的位置为主要因素,不同机构在参数优化时可根据具体机构特性合理选取; (3)优化后全域角的速度传递性能、力矩的传递性能和各向同性性能分别提高了16%、80%、40%,验证了该参数优化方法的有效性。 在后续研究工作中,笔者将进一步研究该机构的精度设计问题,建立机构的误差分析模型,以提高机构的动态精度。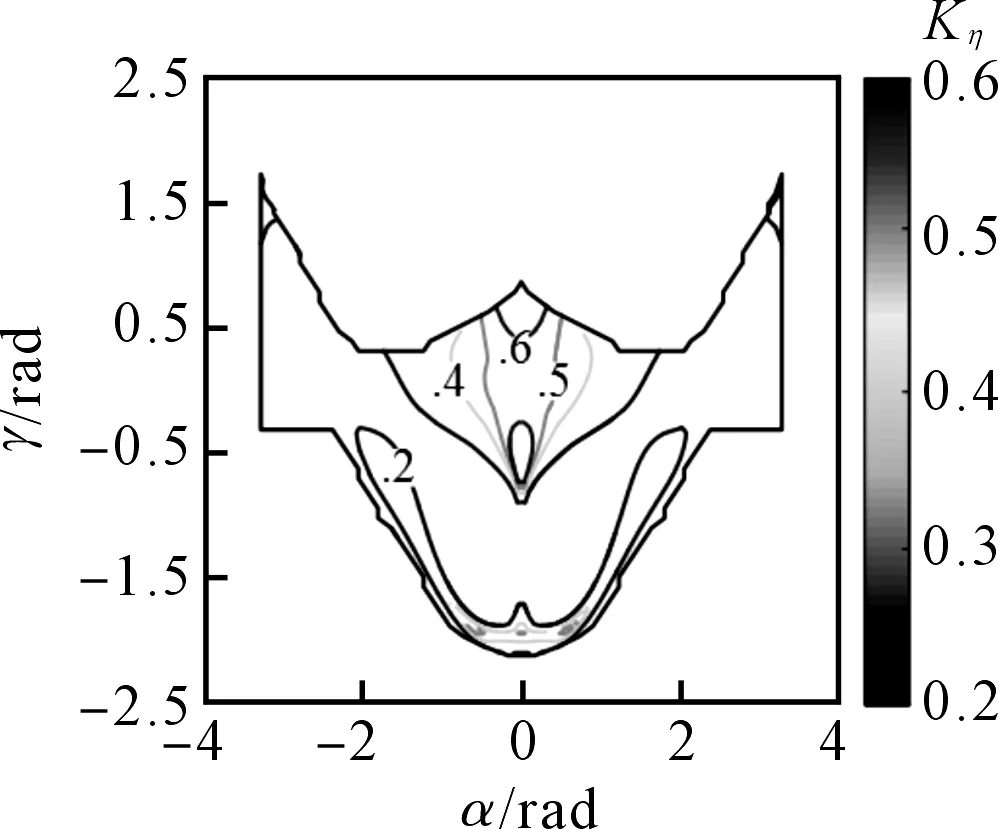
3 结构尺度参数优化
3.1 空间模型技术
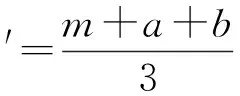

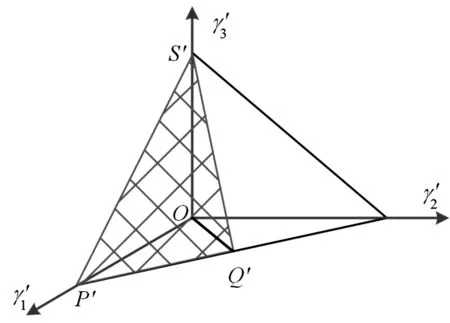
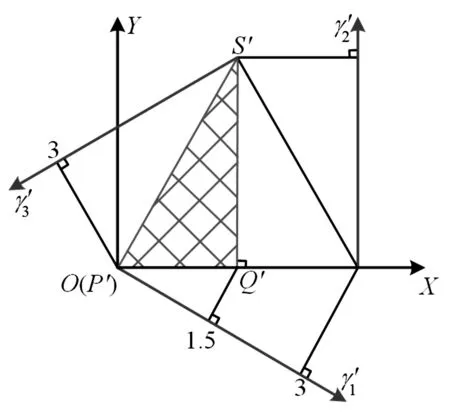
3.2 全域运动学性能评价
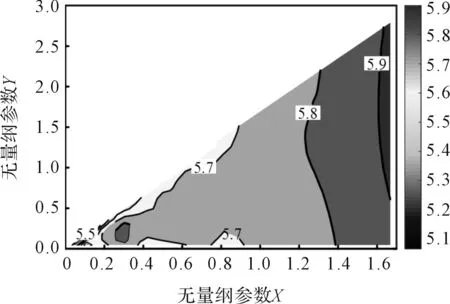

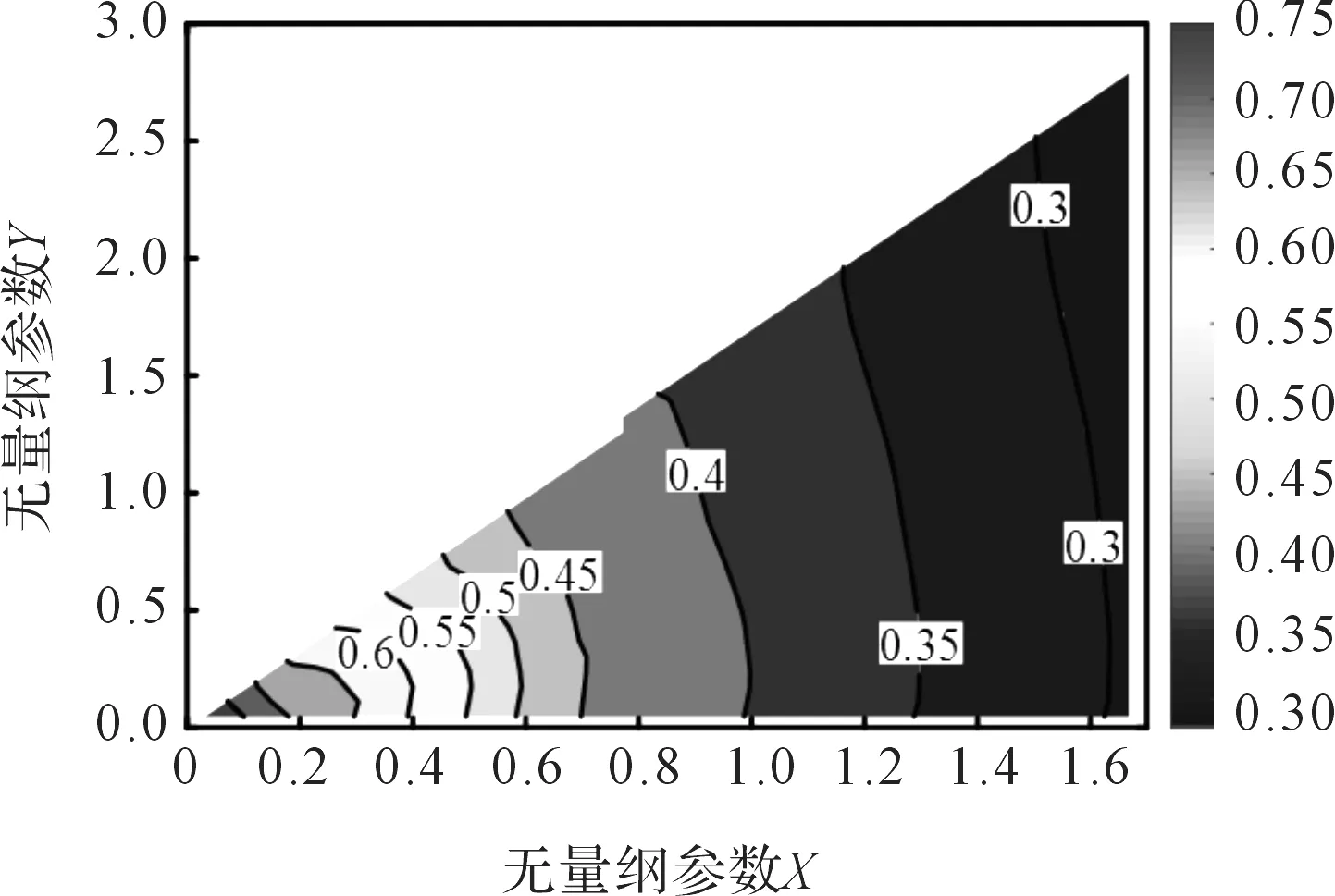
3.3 多目标参数优化
4 结束语

