一种激光雷达和红外摄像头联合标定方法

蒋进军 茅时群 谭兴福

上海振华重工(集团)有限公司

1 引言

随着港口码头智能化升级改造，激光器和视觉融合技术成为当前研究和应用热点。在传统的二维目标检测中，图像识别已经很成熟，通过颜色和纹理很容易分辨出物体的轮廓，特征信息很明显。但二维图像无法准确计算出目标物体的尺寸、距离，而通过激光雷达扫描出点云，可获取物体的纯几何结构、距离、尺寸等相关信息。将图像和点云融合，通过点云获取物体尺寸、位置，然后结合图像分割、识别目标物体，增加物体识别准确度，从而达到很好的互补。

激光器和图像传感器标定是融合技术必不可少的一步，标定的好坏直接关系到后续融合识别、定位的效果。在自动化龙门起重机(以下简称场桥)或岸边集装箱起重机(以下简称岸桥)中，小车架上通常装有摄像头以及激光雷达，用于检测吊具或者集装箱位置[1-2]，如何将摄像头和激光雷达快速、准确进行标定，是传感器使用过程中非常关键的一步[3-4]。结合现场实际使用情况，在吊具上贴两张3M纸，作为标定靶，通过标定靶快速将激光雷达和摄像头进行同步。

2 原理和方法

标定对像是近红外摄像头和激光雷达，均安装在起重机小车架上。

2.1 标定原理

将激光器雷达和摄像头同步，先通过式(1)将激光雷达坐标系变化到摄像头坐标系，然后通过式(2)变换到图像坐标系，最后通过式(3)变换到像素坐标系，从而将点云数据变换到图像中，实现配对。

(1)

(2)

(3)

联合上面3个公式得到公式(4)：

(4)

式中，K只与摄像机内部结构有关,为摄像头内参矩阵，可以通过棋盘格标定方法得到；u、v是特征点在图形中的像素坐标，可以直接通过图片获取；XL、YL、ZL为特征点在激光器雷达中的坐标，可以通过激光器雷达扫描出的点云数据中获取；T为摄像头相对于激光器雷达的变换矩阵,旋转矩阵和平移向量组成，也是最终需要求取的转换矩阵。

其中：

(5)

(6)

为了求取激光雷达到摄像头之间的转换关系，首先通过摄像头和激光雷达分别获取图像信息和点云数据，且保证获取图像和点云数据时外部环境以及自身姿态没有变化，然后分别在图像和点云数据提取出同一特征点。摄像头内参矩阵可以通过棋盘格标定[5-6]出来，结合标定出来的摄像头内参矩阵，n个激光雷达坐标系中的特征点坐标，以及与这n个点对应在摄像头坐标系下的像素坐标，利用EPnP[7]算法，最终求解出T。

2.2 标定方法

为准确获得激光雷达到摄像头坐标系的转换矩阵，结合当前摄像头和激光雷达的特性，需要设计一个标定靶，用于在图像和激光同时精确识别对应数据中特征点，并进行匹配，从而求解出T。

标定靶在设计的时候，需要考虑到图像和激光雷达之间的特征，通过在吊具上安装两个3M反光贴片，标定过程中摄像头拍摄两个3M反光贴片的图像，激光雷达扫描3M反光贴片，然后通过算法分别在图像和点云数据中识别3M贴纸的中心点(见图1)。

图1 标定靶

该标定靶既有矩形标定板的结构简单的优点，同时可以有效消除点云的偏差，保证识别的精度，最终保证激光器雷达和摄像头同步的准确。

3 计算摄像头的外参

3.1 摄像头特征点获取

因为此处标定工作在室外进行，为避免各种光线的干扰，摄像头的补光灯采用的是红外补光灯。近红外摄像头配有红外滤光片，通过滤光片有效滤掉红外波长外的光线。但在实际操作过程中，尤其是夏天阳光直射的时候，阳光的干扰相对严重，因此在实际标定过程中，通过将摄像头光圈尽量调小，进一步降低太阳光的影响。获取图像后，图像进行自适用二值化，然后再对图像进行打标签，根据标签值将图像分割出来，并过滤掉不符合要求的块，再利用分割出来的圆，进行椭圆拟合圆心。

3.2 雷达获取特征点方法

获取点云数据时先提取标定板数据，并得到标定板所在平面方程，将点云数据投影到二维平面，然后将二维平面点转换为图像，在图像中根据能量值进行二值化，提取轮廓，根据轮廓进行椭圆拟合圆心，再根据所获取的椭圆圆心，反求圆心的3D坐标。

3.2.1 标定板数据提取

通过直通滤波，缩小点云数据大小，然后根据激光点能量值，将扫描在3M贴纸上的点提取出来，采用随机抽样一致性进行平面拟合。

随机抽取一批种子点，{pi},i=1,…n，对其求得拟合平面Ax+By+Cz+D=0。向量n(A,B,C)为平面的法向量，即{pi}组成的协方差矩阵的最大特征值对应的特征向量。D为坐标原点到该平面距离，即为{pi}中心点pj和法向量的点乘。

计算所有点pi到平面距离d，d小于阈值dth则为局内点，否则为局外点。

(7)

重复进行迭代，直到找到最优解。最优解对应A，B，C即为平面法向量。

3.2.2 二维坐标投影

由于三维空间点并不完全在一个平面点，因此需要将三维空间的点投影到二维坐标点。p0为平面上任意一点，p为标定板点云，p′为p在平面上的投影点，则投影公式为：

(8)

3.2.3 三维中心点求解

根据激光器扫描点的能量值，将图像进行二值化，在二值化图像提取轮廓图，进行边缘提取，然后利用这些边缘拟合椭圆方式求取圆心，求得中心点(xp,yp)。

(9)

(10)

将中心点x′p和y′p代入平面方程，反向求取z′p，得到三维中心点坐标。

3.3 EPnP求解T

利用n个激光雷达坐标系中的特征点坐标，以及与这n个点对应在摄像头坐标系下的像素坐标，采用EPnP方法来计算出摄像头的外参矩阵T。EPnP算法核心原理是某一坐标系中3D坐标表示为一组虚拟的控制点的加权和。一般控制点选取个数为4个，且4个控制点不共面。激光雷达坐标系中任意一个特征点可由4个控制点来表示，同时摄像头坐标坐标系中任意特征点也可以由4个控制点来表示。求出摄像头坐标中4个控制点坐标后，从而最终计算出摄像头的外参矩阵。在文中的公式中，分别用上标w和c表示在激光雷达中的坐标和摄像头坐标系中的坐标。

3.3.1 控制点基本原理

激光雷达中，每个点可以由4个控制点表示：

(11)

式中，aij为加权系数。一旦控制点确定后，且满足4个控制点不共面前提，aij，j=1,2,3,4是唯一确定的。在摄像头坐标系中，存在同样的加权和关系：

(12)

(13)

进一步可得，

(14)

(15)

已知控制点，则可以求出每个控制点加权系数：

(16)

3.3.2 控制点选择

理论上，控制点选取只要可逆即可。在激光器雷达坐标系中，选择中心作为第一个控制点：

(17)

3D参考点集为：

(18)

记ATA的特征值为λc,i，i=1,2,3，对应的特征向量为vc,i，i=1,2,3，剩余3个控制点按照式(19)来计算：

(19)

3.3.3 求取控制点在摄像头坐标系中的坐标

在摄像头坐标系中，每个特征点同样存在如下加权关系：

(20)

(21)

(22)

(23)

Mx=0

(24)

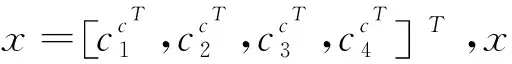
(25)

式中，vi是M的N个零特征值对应的特征向量。对于第i个控制点：

(26)

在激光器雷达坐标系中控制点，通过外参矩阵转换到摄像头坐标中后，两两之间的距离还是保持不变。引入这个约束条件：

(27)

(28)

该方程是关于{βk}k=1,…N的二次方程，主要特点是没有{βk}k=1,…N相关一次项，在求解时，将二次项βiβj替换为βij，将方程变为关于{βij}k=1,…N的线性方程。通过4个控制点，共可以得到6个方程，通过6个方程求解{βij}k=1,…N，然后通过{βij}k=1,…N再求取{βk}k=1,…N。

3.3.4 计算激光雷达到摄像头坐标系的转换矩阵

控制点在摄像头坐标系的坐标为：

(29)

计算每个特征点在摄像头坐标系下的坐标：

(30)

(31)

(32)

计算H：

H=BTA

(33)

计算H的SVD分解：

H=UΣVT

(34)

求取旋转矩阵：

R=UVT

(35)

求取平移t：

(36)

4 标定与测试

4.1 标定

在不同位置，激光雷达和摄像头分别采集标定板数据，共获取20组数据。通过这20组数据，来计算T。具体步骤如下：

(1)利用棋盘格，将摄像头内参进行标定，得到矩阵K。

(2)采集数据，将吊具停止不同高度，然后再分别在对应高度上采集摄像头和激光雷达的数据，共采取20组数据，每组数据中有2个特征点，并将采集的数据按顺序命名，保证图像和点云数据是一一对应的。

(3)获取点云中的40个特征点。

(4)获取图像中的40个特征点。

(5)根据40个特征点，采用EPnP，计算出矩阵T。标定得到的旋转矩阵如下：

(37)

4.2 标定效果测试

在不同高度另外采集10组测试数据，在图像和点云数据中，分别计算3M贴纸的圆心，然后根据获取的T矩阵，以及摄像头的内参矩阵，将激光雷达坐标中的3M贴纸的3D坐标转换到摄像头中的像素坐标系，来验证激光雷达和摄像头的融合标定的精度，见表1。

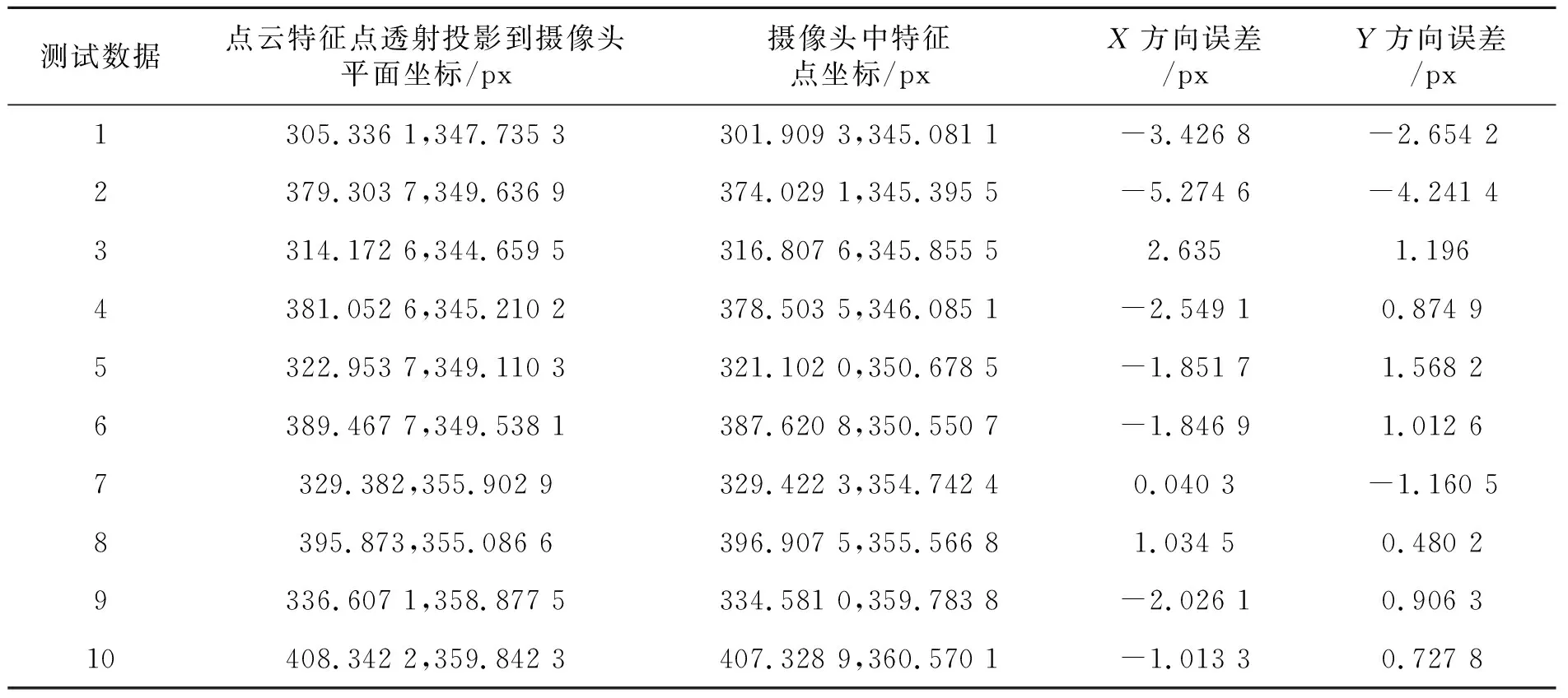
表1 激光雷达和摄像头测试效果

根据表1测试效果，激光器雷达中特征点投影变换到像素坐标系后，最大误差在5个像素左右。标定靶离激光雷达越远，相对误差越大。

5 结语

该方法可以快速精确地将激光雷达和摄像头进行同步标定。在实际使用过程中，如果还需进一步提高标定精度及抗干扰能力，可以继续增加标定特征点数目或者增加点云数据量，提高点云特征点精度，最终降低标定误差。实际测试过程中，该标定方案可靠，精度高，完全满足应用要求。