基于置信度神经网络的机载武器攻击区拟合算法
张超然,吕余海
(海军研究院,上海 200020)
0 引言
机载武器攻击区是飞行员判断导弹发射时机的重要依据,准确的攻击区是有效完成空战任务的重要保证。目前,机载武器攻击区计算主要包括理论计算法、插值算法和拟合算法等[1]。理论计算法利用武器模型,根据发射条件,通过解算微分方程组得到攻击区[2-3],计算的攻击区较为精确,但是计算量大,实时性不高。插值算法需要离线计算全面的攻击区数据,建立攻击区数据表,再根据当前状态进行插值计算,需要庞大的存储资源。拟合算法是利用离线样本数据,拟合导弹发射参数与攻击区间的映射关系,将拟合参数装载到火控系统[4],火控系统根据实时的发射状态计算攻击区。
传统拟合算法包括多项式拟合、三角函数拟合等,此类方法依赖于模型的准确性,而由于攻击区的高度非线性,无法进行精确的拟合。基于神经网络的拟合算法无需对函数进行建模,可以利用输入输出样本,直接对神经网络进行训练,可有效提高攻击区计算精度[5-6]。
神经网络拟合算法的估计效果严重依赖于样本的数量与质量,受到飞行试验成本的限制,可利用的导弹真实飞行数据往往较少且不全面,攻击区拟合算法一般需要大量飞行仿真数据作为训练样本。然而,由于仿真与导弹实际飞行的真实性存在差距,仿真得到的数据置信度往往低于实际飞行试验数据[7],由于传统神经网络算法无法区分不同样本,导致少量实际飞行数据对估计结果的影响很小,算法无法有效的利用这些数据的信息。
文中研究基于置信度神经网络的机载武器攻击区拟合方法,区分不同置信度的训练样本,既能有效利用仿真飞行数据的全面性,又能有效利用少量飞行样本数据的真实性,拟合得到更为精确的机载武器攻击区。
1 神经网络攻击区拟合方法
机载武器攻击区主要由载机高度、发射速度、离轴角、目标高度、速度、以及目标过载等因素决定,攻击区是这些因素的复杂非线性函数,可表示为:
Rmax=f(ha,va,θat,ht,vt,nt)
(1)
式中:Rmax为最大攻击距离;ha为载机高度;va为载机速度;θat为导弹发射离轴角;ht为目标高度;vt为目标速度;nt为目标水平过载。
神经网络拟合方法是将X=[ha,va,θat,ht,vt,nt]等导弹发射参数作为网络输入,将Y=[Rmax]等作为网络输出,利用大量样本对网络进行训练,得到训练后的网络Y=net(X)。在机载火控系统计算时,根据不同的输入参数,利用训练后的网络对攻击区进行估计。神经网络拟合算法流程如图1所示。
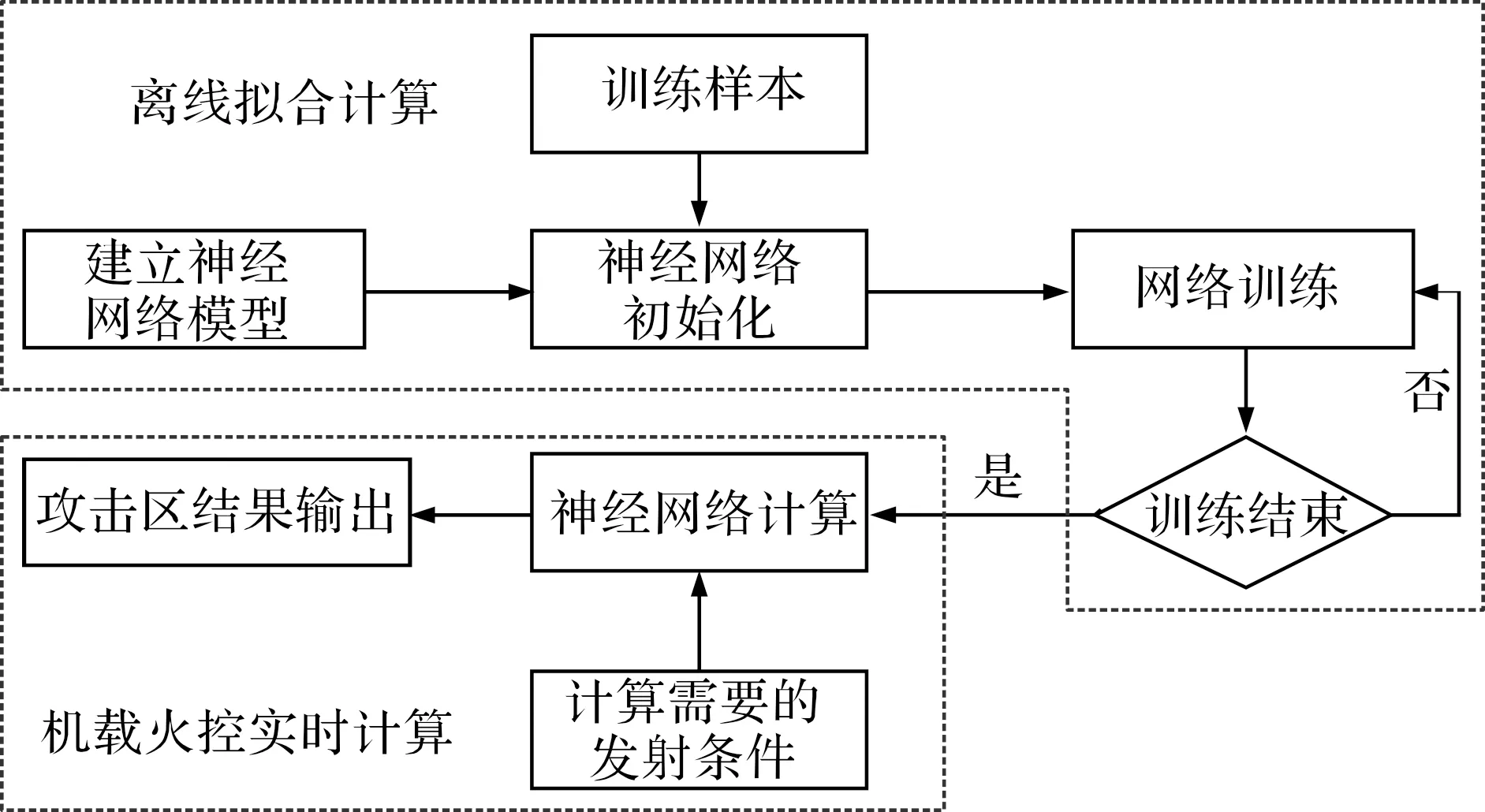
图1 神经网络机载武器攻击区拟合方法流程
步骤1,建立神经网络模型。根据攻击区计算的输入输出个数、非线性映射特点,建立神经网络的结构。根据式(1)的攻击区拟合问题,输入层为6个节点,输出层节点数根据需要得到的攻击距离个数确定,可利用3层或4层神经网络逼近该非线性映射。
步骤2,神经网络初始化。神经网络初始化包括各连接权值、阈值的初始化,以及弹道样本的归一化等处理。对弹道样本归一化的处理,可把高度、速度、角度等数据转化为0~1的数,取消不同物理量之间的数量级差别,避免样本因数量级差别过大造成网络训练失败,归一化可以使用最大最小法、平均数方差法等。
步骤3,利用样本对神经网络进行训练。训练主要包括隐藏层输出计算、输出层输出计算、误差计算、权值更新、阈值更新等。
隐藏层输出的计算,根据样本中的发射参数等输入及连接权值、阈值,并采用激励函数计算隐藏层输出,为保证神经元的非线性,可选用S型传递函数作为激励函数;输出层的计算,根据隐藏层输出、隐藏层-输出层连接权值以及输出层阈值,并采用激励函数计算输出。误差的计算,利用样本减去神经网络输出,获得神经网络的预测误差。根据网络预测误差,利用学习算法更新网络中各连接权值和节点阈值。
步骤4,判断神经网络是否训练结束。根据预设的训练次数或者期望达到的误差门限判断是否完成训练。如果未完成训练,则再进行网络训练,如果训练结束则保存网络参数。
步骤5,机载火控系统攻击区计算。前4个步骤均是在地面离线完成,完成训练后将网络参数加载到机载火控系统中,机载火控系统根据当前时刻导弹发射参数,实时计算机载武器攻击区。
2 置信度神经网络攻击区拟合方法
机载武器的实际飞行数据个数远少于仿真飞行数据个数,而且由于仿真条件与真实环境存在一定的差距,大多数情况下,仿真得到的样本相对于真实情况都存在误差,这导致了仿真飞行数据与实际飞行数据存在不同的置信度。如果将其简单的组合,利用传统神经网络同时处理,实际飞行数据所起的作用很小,甚至在实际飞行数据偏离仿真飞行数据较大时,可能会导致真实数据被视为野点,或者导致网络的过拟合。
因此,需要对具有不同置信度的数据进行区分处理,既能更好地拟合少量高置信度数据样本,又能充分的利用低置信度样本信息。
基于置信度神经网络的机载武器攻击区拟合方法主要分为两步:第一步利用仿真飞行数据对网络进行训练,得到先验网络net1(X);第二步利用实际飞行样本对标准神经网络的输出误差修改,进行二次训练,得到置信度神经网络net2(X)。
如果两次神经网络都是经过良好训练的,先验神经网络输出可视为置信度神经网络的输出加入误差:
net1(X)=net2(X)+ε(X)
(2)
由于仿真飞行样本误差来源的复杂性,噪声既包含一部分确定成分又包含一定自相关性的不确定成分,因此噪声一般包含常值偏置部分以及随机偏差部分。
文献[8]根据贝叶斯公式,建立并推导了net1(X)与net2(X)之间的误差期望E(ε(X))范围,根据εi=Yi-net1(Xi)的正负将E(ε(X))的范围分为以下3种情况:
(3)
式中:‖‖表示取范数;ri为实际飞行样本的影响范围,超出该范围后,误差期望值受实际飞行样本的影响将衰减到10%以下。
利用式(3)可以求出每一个仿真飞行样本的误差容量区间[edj,euj],容量区间的上、下限对应式(3)的最大、最小值。利用误差容量区间对net2(X)的网络预测误差进行修正,再利用修正后的误差对网络的权值、阈值进行训练,训练学习算法会在net1(X)+ed和net1(X)+eu之间寻找到一个相对合适的综合神经网络模型,实现提高对实际飞行数据样本拟合程度,以及充分利用仿真飞行数据信息的目的。具体实现流程如图2所示。

图2 置信度神经网络攻击区拟合方法流程
步骤1,建立标准神经网络,利用仿真飞行数据样本(Xj,Yj)对神经网络进行训练,获得神经网络Y=net1(X)。
步骤2,计算每一个实际飞行数据样本(Xi,Yi)与该神经网络输出之间的误差εi=Yi-nets(Xi),根据实际飞行数据的影响范围ri求出每个仿真飞行数据样本的容量区间[edj,euj],容量区间的上下限对应式(3)的最大最小值。
步骤3,利用实际飞行数据样本、仿真飞行数据样本进行第二次神经网络训练,将仿真飞行数据样本的神经网络预测误差修改为:
(4)
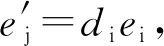
步骤4,根据发射参数输入,利用net2(X)网络进行机载武器攻击区计算。
3 仿真分析
选取某型空空导弹的理论攻击区进行仿真分析,在理论攻击区上叠加随机噪声、常值偏差作为仿真飞行数据样本,选取部分理论攻击区数据作为实际飞行数据样本,分别对传统神经网络以及置信度神经网络进行训练,对比传统神经网络和置信度神经网络的攻击区拟合效果。神经网络的结构为6-7-1,即输入层6个节点,隐藏层7个节点,输出层1个节点,隐藏层激励函数为sigmoid函数,输出层的激励函数为purelin函数,并采用Levenberg-Maquardt方法进行训练。
图3为攻击区拟合结果,图3(a)为在随机噪声情况下的估计结果;图3(b)为随机噪声加负常值偏差情况下的估计结果;图3(c)为随机噪声加正常值偏差情况下的结果。仿真飞行数据样本远多于实际飞行数据样本,实际飞机数据样本只有4个,从结果中可以看出,置信度神经网络能够得到更好的拟合实际飞行数据样本,估计的攻击区与理论攻击区之间的误差更小。在存在负常值偏差的情况下,传统神经网络算法拟合的攻击区明显偏小,导致失机发射概率过大。在存在正常值偏差的情况下,传统神经网络拟合的攻击区明显偏大,导致界外发射概率过大,这两种情况会导致飞行员对武器攻击边界误判,而置信度神经网络可以有效的利用实际飞行数据样本将拟合的攻击区进行修正。
对两种算法的失机发射概率Pml、界外发射概率Pab和成功发射概率Pst进行统计,结果如表1所示。从表1中可以看出在各种噪声情况下,置信度神经网络算法能够有效抑制仿真飞行数据样本的常值偏差和随机噪声影响,能够有效减小攻击区估计误差,提高武器发射成功概率。

表1 两种拟合方法的结算精度比较
4 结论
提出了一种基于置信度神经网络的机载武器攻击区拟合算法,算法可将实际飞行数据有效的应用于攻击区的校核,有效提高机载攻击区计算的准确性,是将少量的实际飞行数据应用于攻击区估计的有效手段。在作战实验、演习中应注重实际飞行数据的采集,并可利用该算法对现有攻击区进行修正,进一步提高估计的准确性。

