基于动静混合传感器网络的路域降雨量分布估计方法研究

任 欣，张建国

（长安大学 电子与控制工程学院，陕西 西安 710064）

0 引 言

近年来，随着交通运输业的蓬勃发展，道路交通安全事故频发，而路面雨水是引发事故的主要原因之一。路面雨水导致路面摩擦系数明显下降，车辆制动性变差，易出现车辆打滑、侧滑或车轮空转等失控现象，极易诱发严重的交通事故[1-2]。因此，实时掌握目标路域内的降雨量信息，能有效地对目标区域内车辆进行管控[3]，避免交通事故发生，确保行车安全。

目前，利用传感器网络估计目标区域信息分布状态的算法研究颇多，尤其是针对时变且未知的信息分布状态。例如，文献[3]根据移动传感器网络的采样信息，实现了对目标海域的有效监测。文献[4]设计了一种基于高斯估计的自适应估计算法，有效地预测出了目标区域内的有效信息分布。文献[5]提出了一种基于卡尔曼滤波与RBF神经网络的信息分布估计算法，有效地估计出了含有噪声的未知目标区域的信息分布。文献[6]给出了一种分布式的环境模型，并提出一种控制律能够最大化传感器感知的信息。文献[7]利用贝叶斯估计算法，实现了多智能体在时变环境下的最优覆盖目标。文献[8]提出了一种分散式的自适应空间估计算法来近似逼近目标区域内的信息分布。

在理论方面，对于目标区域内的降雨量分布估计方法研究成果较少。例如，文献[9]利用RBF神经网络估计地面的降雨量分布。文献[10]提出了一种基于密度参数K-means算法的RBF神经网络预测模型，能够有效预测短期降雨量。文献[11]针对研究区域的降雨量分布情况，建立了一种基于BP神经网络的空间插值估算模型，实验结果表明该模型在小区域范围或雨量密度分布均衡的情况下，估计精度较高。文献[12]针对极端天气下异常降雨量分布，建立了一种基于极值理论的极端降雨量估计模型，并通过实验检验了其所得分布。然而，上述文献主要侧重于某一范围的降雨量分布，无法获取连续路域内的整体降雨量分布，本文针对此类问题展开了研究。

由上述研究分析可知，估计目标区域内降雨量分布的研究大多数局限于小区域，且在计算精度与计算速度方面均有待提高。针对此类需求，本文进一步研究动静混合传感器网络对公路路域内降雨量分布估计，主要贡献包括：

（1）设计公路路域内降雨量分布估计模型，针对公路路域的窄长型空间分布特性，合理选择径向基函数中心点位置，有效地提高了估计算法的准确度。

（2）由于目标区域内降雨量的时变性，提出一种基于采样误差的动态采样机制，其目的在于尽可能地避免传感器采集数据冗余，造成计算资源浪费。

（3）根据动静混合传感器网络的动态采样机制，设计一种基于卡尔曼滤波方法的降雨量估计算法，预测目标区域内的降雨量分布状态，并以降雨量的估计误差为目标函数，根据梯度下降法，通过调整移动传感器采样位置的手段，进一步优化对公路路域内降雨量分布的估计结果。

1 降雨量分布估计模型

考虑n个传感器监测公路路域Q∈R2内的降雨量分布，其中q∈Q表示区域Q内任意一点的位置。

定义mi为第i个移动传感器，M表示移动传感器的集合，即mi∈M, i=1, 2, ..., nm。此外，在路域Q内分布ns个固定传感器，S表示固定传感器的集合，即sk∈S, k=1, 2, ..., ns。因此，传感器的数量n=nm+ns。

公路路域Q的降雨量分布状态表示为φ(q, k)，假设φ(q, k)由径向基函数组成，其降雨量分布估计模型表示为：

式中：ψT(q)=[ψ1(q), ψ2(q),..., ψl(q)]表示基函数组成的向量；x(k)=[x1(k), x2(k),..., xl(k)]T表示时变的状态向量。

由式（1）知，降雨量分布状态φ(q, k)的估计取决于两方面：径向基函数与状态向量。针对公路路域降雨量估计，定义径向基函数，以公路路面为中心，确定公路两侧和公路路面上的径向基中心点。本文选取高斯函数作为径向基函数，具体形式如下：

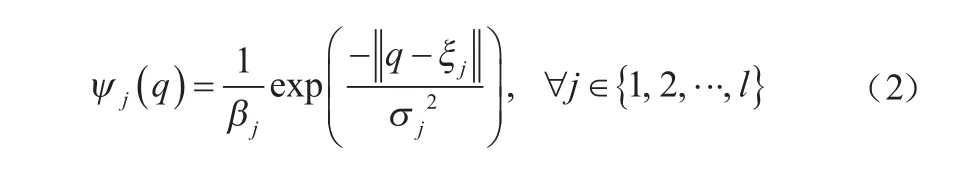
式中：σj是高斯基函数的宽度；βj是归一化常数；ξj是基函数的中心点。

在此基础上，公路两侧中心点的选取如下：

式中：i=1, 2, ..., ns表示固定传感器的个数；a表示中心点的选取个数；d1表示目标区域内公路的长度；d2表示公路两侧的宽度；b表示公路两侧中心点所在的总行数；j表示第j行。

公路路面上中心点的选取公式如下：

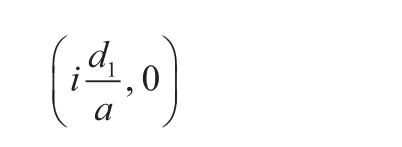
式中i=1, 2, ..., nm表示移动传感器的个数。

在此基础上，本文利用多移动传感器网络更新状态x(t)，从而估计公路路域降雨量分布(q, k)。本文假设每个传感器均能采集其所在位置上的信息。

2 降雨量分布估计算法

2.1 动态采样机制

在实际情况下监测区域往往是动态变化的，即随着时间的变化，路域内降雨量分布也会发生变化。在此基础上，提出一种动态采样策略，即存在固定的传感器执行周期T，在一个执行周期内当前的采样值与前一个执行周期采样均值的差值大于设定的数值时改变下一次的采样间隔。如图1所示，每个执行周期内存在多个采样周期。通过动态调整执行周期内的采样周期，进而提升估计算法的运算效率。

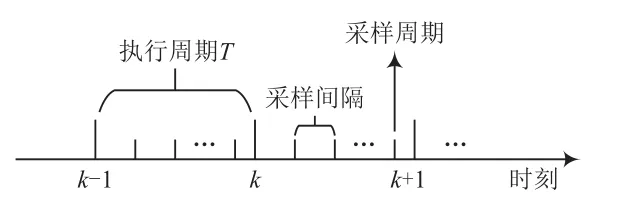
图1 采样时刻

2.2 基于变采样的分布估计算法

假设模型（1）中的状态x(k)=[x1(k), x2(k), ..., xl(k)]T可由线性动态系统（4）得到。

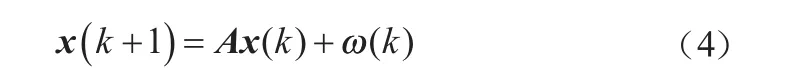
式中A∈Rl×l表示系统矩阵。假设状态x的下一时刻与当前时刻是稳定变化的，总是存在一个合适的A，能够准确地描述状态x的当前状态与下一状态之间的关系。噪声ω∈Rl为零均值高斯白噪声，方差记为W。

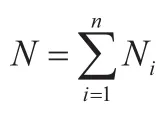
2.3 最优采样位置

值得注意的是，提出的控制器fi过小将导致传感器不能快速的响应，其可能出现的原因有：

（1）协方差矩阵P很小甚至下一步传感器没有移动；

（2）Φ(pi)和K(pi)的梯度很小；

（3）控制增益Kf太小。

此外，控制器fi仅仅是关于径向基函数的集合｛ψi(v)｝，控制增益Kf，矩阵P，噪声以及相关矩阵S的函数，并不是直接与估计状态有关。同时，传感器的位置和环境监测的模型影响着梯度下降控制律。

此外，针对增益Kf的选择，当增益充分小的时候，能够保证传感器移动位置的准确性，但会造成移动缓慢的现象；当增益太大时，会导致传感器的移动位置不稳定，出现振荡，同时代价函数J的值也会增大。

3 仿真实验

考虑采用40个传感器对公路路域降雨量分布进行监测，监测区域取10 km×10 km的正方形区域，固定传感器随机分布在路域两侧，ns=30。移动传感器分布在路域上，nm=10。径向基函数中心点选取d1=10 km，a=5，d2=4 km，m=2。移动传感器的控制律由式（30）描述，每个传感器的采样噪声为高斯白噪声，估计误差协方差矩阵P0=Il×l，状态x的初始值取[-10, 10]之间的随机数。

监测区域的真实信息分布表示如下：

分析上式可知，目标区域的峰值在0≤t<15的时间段内，由(10, 6)匀速移动到(8.5, 5.85)；随后当15≤t<100时，峰值从(8.5, 5.85)匀速移动到(5.5, 5.5)；当t≥100时，不再发生变化。在此基础上，本文所提估计算法的仿真结果如图2所示。

图2 动静混合传感器降雨量分布估计仿真

图2展示了各个传感器位置及其目标监测区域。其中，图2（a）为各个传感器的初始位置。图中窄长型区域表示公路路域，区域内的彩色背景表示路域内降雨量，其中每种颜色所对应的降雨量值由其旁边的色彩幅值对应表显示，如黄色区域即表示该区域内的降雨量较高，图中的红色星号表示固定传感器的采样位置，黄色圆圈表示移动传感器初始时刻的采样位置，移动传感器的移动轨迹由蓝色线条表示，蓝色圆圈是移动传感器最终的位置。从图中可以看出，在初始阶段，目标区域内降雨量较高的区域集中在公路右侧。图2（b）为各个移动传感器在t=50 s时的位置及传感器的移动轨迹，在控制律（30）的作用下各个传感器能够实时移动自身的位置来采集区域的信息。在图2（c）中，信息分布峰值到达预先设定的位置，同时图中展示了各个传感器在目标区域内移动的完整轨迹。仿真结果表明，基于动静混合传感器的公路路域降雨量估计方法能够实时地估计时变情况下的降雨量分布。进一步详细的仿真结果如图3、图4所示。

图3 状态x的变化曲线

图3为提出的估计算法中的状态x的变化曲线，从图中可以看出，状态x的变化趋于稳定，即从前一时刻的状态到当前时刻的状态基本处于稳定变化，因此通过状态的变化曲线进一步说明了目标区域降雨量分布估计的准确性。

图4为降雨量估计方法平均估计误差。由该仿真结果可知，随着时间的增加，该平均估计误差保持收敛。因此，本文所设计的估计算法能够准确地估计出目标区域内随时间变化的降雨量分布。这一仿真结果验证了本文设计的估计算法的有效性与可行性，也进一步证明了动态采样机制的优越性。

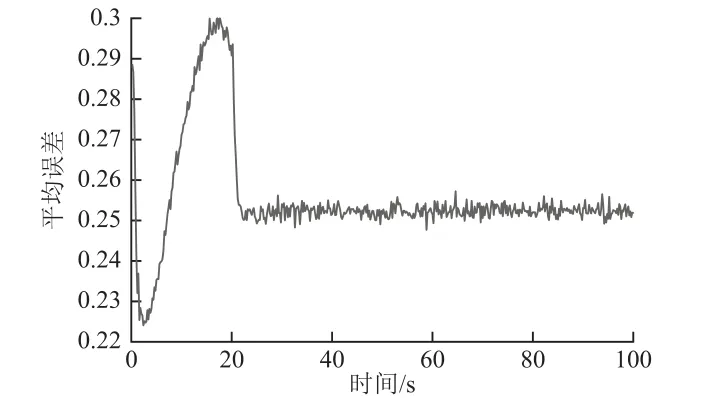
图4 平均误差的变化曲线

4 结 语

本文针对路域内降雨量分布的估计问题，提出一种基于动态采样机制与卡尔曼滤波方法的估计算法。首先，设计降雨量分布估计模型，针对公路的窄长型区域，给出一种径向基函数中心点选取方法；接着提出一种基于采样误差的动态采样机制，在此基础上，设计基于卡尔曼滤波方法的信息分布估计算法，给出当前采样信息的信息分布结果；其次，以信息分布的估计误差为目标函数，利用梯度下降算法调整移动传感器采样位置，进一步优化信息分布结果；最后，通过仿真实验的手段验证了本文提出的估计算法的可行性与有效性。