某大型低温火箭高空风载荷分析

王建明，林 娜，张博戎

（1. 北京宇航系统工程研究所，北京，100076；2. 航天材料及工艺研究所，北京，100076）

0 引 言

大型运载火箭是中国未来中长期航天发展的主力，承担首次火星探测、月球探测和空间站建设等重大发射任务[1]。迄今为止，该火箭开展了6次飞行试验，完整地获取了各项遥外测数据，具备开展飞控品质评定和箭体承载能力余量分析的基础。

运载火箭气动外形相对简单，且不在稠密大气层内长时间平飞，因而一般不对动压头和气动攻角、马赫数等进行高精度测量。工艺散差、材料散差是客观存在的，根据静力试验数据难以精确评估一发火箭的实际承载能力。文昌航天发射中心场区0～30 km高空风变化规律与中国酒泉、西昌和太原等内陆“西风带”发射场存在显著差别[2,3]。为了科学减重，稳妥提高火箭运载系数，本文结合某大型火箭飞行数据和发射日风场数据对火箭飞行Qα值及其偏差包络开展分析。

某大型火箭尚处于早期应用发射阶段[1]，飞行Qα分析对改进设计和飞控品质评定，载荷及力学环境优化、发射概率评估等工作具有重要意义。

1 风载荷分析计算模型

工程上，一般通过平台或捷联惯组确定运载火箭实际的飞行速度、位置和姿态信息。火箭相对制导导航基准坐标系的速度、位置和姿态角信息一般也会通过测量系统发回地面，供结果分析和改进设计使用。

为开展火箭飞行Qα值分析工作，需要使用箭上下传的发惯系姿态、速度和位置数据。

1.1 坐标系

为研究高空风对火箭绕心运动的影响，本文需定义以下坐标系[4,5]：

a）北天东坐标系；

b）地心地固坐标系；

c）发射坐标系；

d）发射惯性坐标系；

e）箭体坐标系；

本文使用的基本坐标系及其欧拉角含义、方向余弦矩阵等参见航天器常用坐标系规范。

1.2 风速矢量

大气相对地球运动速度称为风速，用Vw表示。火箭飞行中，风速矢量在北天东坐标系的分量计算公式为

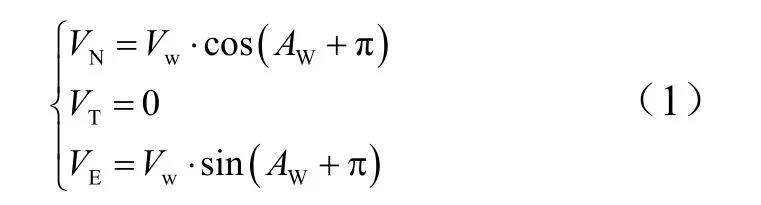
式中VN为高空风北向分量；TV为高空风天向分量；EV为高空风东向分量；wV为风速；WA为风向。

风速矢量在地心地固坐标系、发射坐标系和发射惯性坐标系分量计算方法如下：

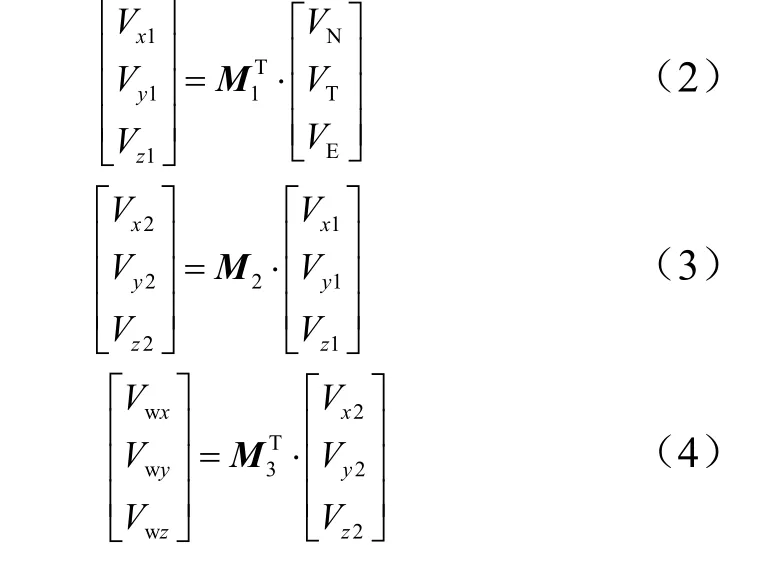
其中，

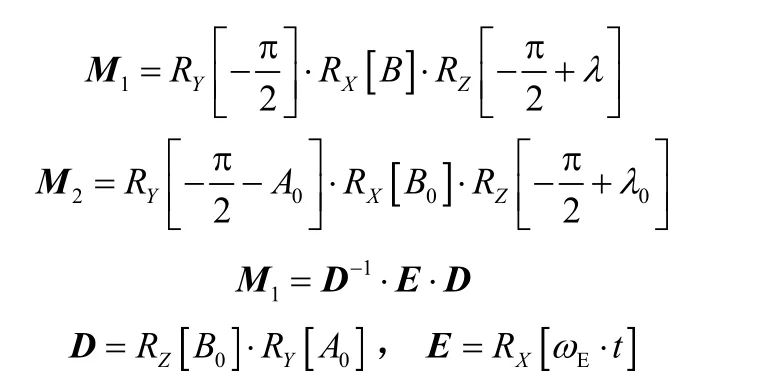
式中Vx1，Vy1，Vz1为高空风在地球坐标系风速分量；Vx2，Vy2，Vz2为高空风在发射坐标系的风速分量；Vwx，Vwy，Vwz为在发射惯性系的风速分量；RX，RY，RZ为绕X、Y和Z轴的变换矩阵。

通过箭下点经度λ、大地纬度B，发射点经度0λ、发射点大地纬度0B和射向0A、地球自转角速度Eω、累计飞行时间t等参数即可给出风速矢量在发射惯性系分量。

1.3 地速矢量

火箭相对地球的运动速度称为地速，用表示。火箭飞行过程中，地速矢量可用通过惯组导航数据给出：

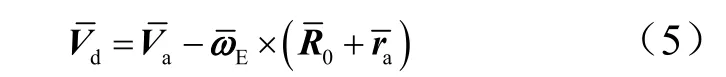
相对发射惯性系，地速矢量形成的弹道倾角θd、航迹偏航角σd：

式中Vdx，Vdy，Vdz为火箭地速分量。

符合小角度线性化的假设条件下，地速形成的攻角dα、侧滑角dβ计算模型如下，

式中κ为俯仰姿态角；ψ为偏航姿态角。

按式（5）～（9）可通过发射惯性系位置、速度和姿态数据给出地速攻角、侧滑角信息。

1.4 空速矢量

火箭相对“来流”的运动速度称为空速，用表示。空速矢量地速、风速矢量做差计算，见式（11）。

相对发射惯性系，空速矢量形成的弹道倾角θq、航迹偏航角σq：

符合小角度线性化的假设条件下，地速形成的攻角αq、侧滑角βq计算模型如下：

根据矢量投影关系：

式中dα，dβ分别为地速矢量产生地速攻角和地速侧滑角；wα，wβ分别为风速引起的附加风攻角、侧滑角。

2 发射日高空风测量

文昌航天发射中心气象站具备多种高空风探测能力，包括风廓线雷达、L波段探空仪器、GPS探空仪和北斗探空仪。

风廓线雷达具有操作简单、实时性强等优点，但硬件设备难以长时间连续运转，且天气条件对风廓线雷达测风数据的质量有显著影响。受探空气球吊载能力和升空速度限制，L波段、GPS、北斗测风仪的高空风探测0～30 km高度的风场一般需要1～1.5 h。

统筹考虑各种探测方案优缺点，中国航天发射任务保障采取以GPS/北斗探空仪为主，风廓线雷达为辅的方案。为进行飞行Qα值分析，通常在射后0.5 h补充进行一次高空风探测，并认为该风场是最接近火箭实际感受的高空风。

任务期间，发射场系统提供的射后+0.5 h北向、东向风速剖面分别见图1和图2。迄今为止，某大型火箭共进行了6次飞行试验任务，对应图中编号01～06，发射窗口涵盖冬季、夏季、春季。

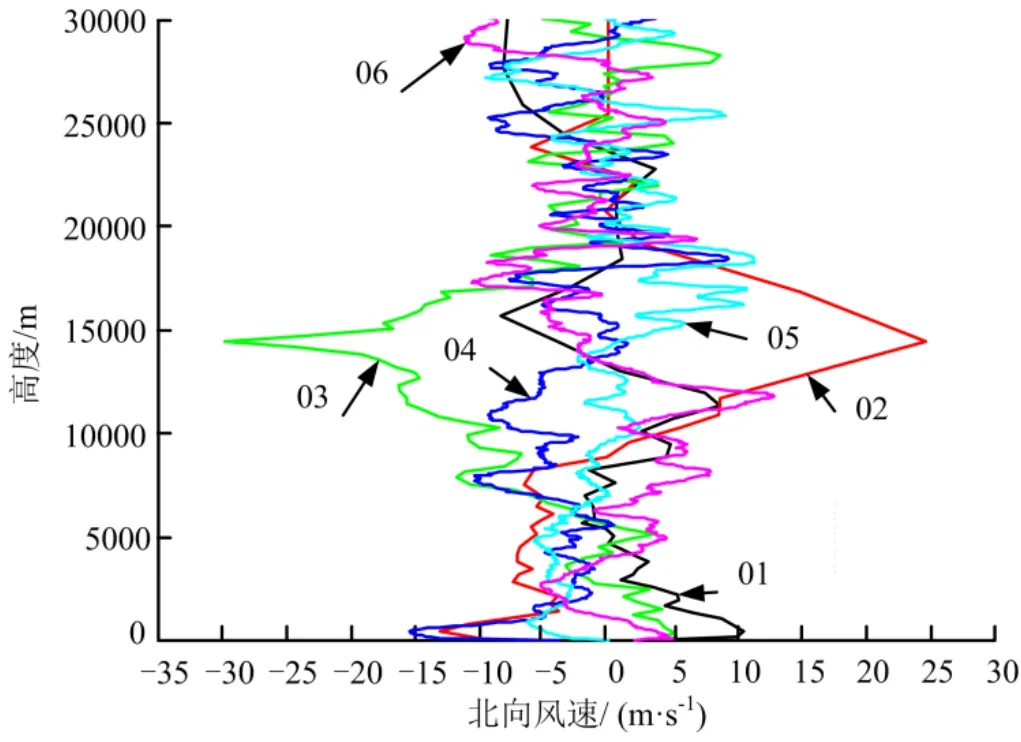
图1 发射窗口北向风速剖面Fig.1 North Wind Velocity Profile of Launch Windows

图2 发射窗口东向风速剖面Fig.2 East Wind Velocity Profile of Launch Windows

上述风场数据表明，文昌航天发射中心场区高空风规律与中国内陆发射场存在显著差别。其风场特点集中体现在：风速不大，8～12 km火箭最大动压区高空风速仅25～30 m/s；风向多变，不具有明显“西风”特征。部分季节时间内，南风可能成为优势风。

3 火箭飞行Qα值分析

高空风载荷Qα值与火箭的载荷及力学环境、特别是弯矩载荷密切相关，也是火箭研制阶段确定结构设计要求的重要依据。本章结合大型火箭飞行试验数据，对其中的关键参数进行分析。

3.1 动压头

动压头对气动力、力矩和发动机配平力矩具有重要影响。首先，求解实际飞行中火箭的飞行速度、高度、航程和箭下点经度、纬度等参数；其次，采用标准大气模型插值计算火箭各飞行高度上的大气密度、当地音速等参数；最后，根据火箭空速、大气密度计算各层高上的动压头。

某大型火箭飞行中，0～30 km高度范围空速引起的动压头见图3。CZ-5系列火箭最大动压区集中在约11 km高度，最大动压量级约26～29 kPa。

图3 作用在火箭上的动压头Fig.3 Aerodynamic Head on Launch Vehicle

图3表明，高空风通过影响火箭与“来流”相对速度的方式最终影响动压头。风速量级相对较小，作用在火箭上的动压头主要受火箭自身运动的影响。

3.2 地速攻角和侧滑角

不同于航空器，运载火箭气动外形相对简单，飞行控制一般不直接测量攻角和侧滑角。通过惯组测量数据可对实际飞行中的地速攻角、侧滑角变化历程进行反演，地速攻角、侧滑角直接反映了火箭飞控品质，是评定火箭总体性能的重要依据。

某大型火箭飞行中，0～30 km高度范围火箭地速攻角、侧滑角见图4和图5。

图4 地速攻角Fig.4 Attack Angle of Launch Vehicle Velocity

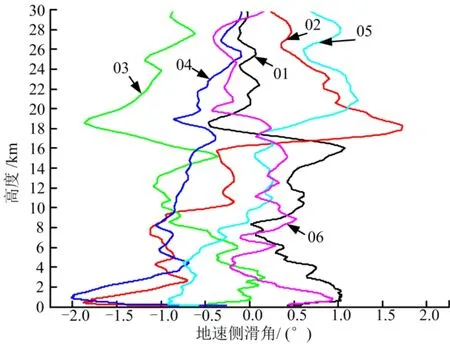
图5 地速侧滑角Fig.5 Sideslip Angle of Launch Vehicle Velocity

数据分析表明，11 km高度范围火箭穿越最大动压区前后地速攻角约1°，侧滑角约1°；稠密大气层内飞行段，全程最大地速攻角约-2.5°、最大侧滑角-2.0°。某大型火箭飞控品质良好，箭体姿态变化能快速跟踪程序角变化。

3.3 风速攻角和侧滑角

为分析高空风对火箭运动的影响，需要根据火箭相对“气流”的速度：首先，计算空速在发射惯性系的分量；其次，求出空速形成的弹道倾角、航迹偏航角；最后，从总弹道倾角、航迹偏航角中分别扣除地速弹道倾角、航迹偏航角得出高空风引起的附加风攻角和侧滑角。

某大型火箭飞行中，0～30 km范围高空风引起的附加风攻角、侧滑角见图6、图7。

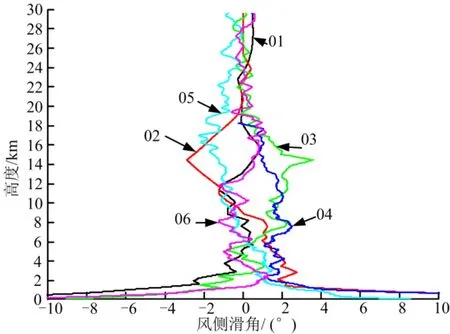
图7 高空风引起的风侧滑角Fig.7 Sideslip Angle of Wind Velocity

程序转弯早期，比如0～5 km范围火箭地速与风速处在同等量级，高空风引起的附加风攻角、侧滑角高达10～20°。垂直起飞及出塔段动压压头相对较小（与最大动压区存在数量级差异），高空风导致的弯矩载荷并非影响火箭安全的主要矛盾。

3.4 高空风载荷

求解出动压头、地速攻角、地速侧滑角、风攻角、风侧滑角的基础上，根据小角度线性化假设计算不同高度层上火箭高空风载荷的飞行值。

某大型火箭飞行Qα值随高度的变化曲线见图8。迄今为止，该型火箭所有发射任务飞行Qα值仅验证至放行门限的65%。

图8 高空风载荷Qα飞行值Fig.8 Flight Wind-load for Large Cryogenic Launch Vehicle

迄今为止，该大型火箭共进行了6次飞行试验，助推飞行段均飞行正常，实现了制导关机，但总体仍处于早期应用飞行阶段。

为充分兼顾火箭总体性能、运载能力、发射概率和飞行安全等研制需求，亟需继续积累飞行试验数据，在满足Qα放行门限要求情况下，逐步对箭体实际承载能力进行验证。以不影响火箭可靠发射使用为前提，适当调整Qα值放行门限，科学稳妥减重，不断提升结构效率和运载系数。

4 结 论

为改进火箭设计，本文提出一种飞行Qα间接反演方法，对某大型低温火箭稠密大气层内飞行段0～30 km范围动压头、地速攻角和侧滑角、附加风攻角和侧滑角、高空风载荷Qα等进行分析，为火箭结构承载余量评估和稳妥减重提供了依据。

分析表明：a）火箭穿越最大动压区前后，地速攻角、侧滑角及风攻角、侧滑角量级较小，火箭姿控能力尚有余量，飞控品质良好，减载方案设计合理；b）火箭飞行Qα值达到放行门限的65%，结构效率和载荷精细化水平尚有一定的提升空间。

为覆盖和包络场区历年统计风场，后续可结合实际飞行的地速攻角、侧滑角进行组合偏差打靶，优化火箭高空风载荷放行门限。