基于改进的Green-Ampt入渗模型的炭质泥岩粗粒土路堤边坡稳定性分析
何忠明,钟魏,刘正夫,李奇,舒青海
(1.长沙理工大学交通运输工程学院,湖南长沙,410004;2.长沙职业技术学院建筑与艺术设计学院,湖南长沙,410217;3.昆明空投建设管理有限公司,云南昆明,650000)
炭质泥岩在我国西南地区广泛分布,饱水之后具有易软化崩解、变形大等特点,一般很少作为路堤填料使用。随着我国西南地区交通建设的不断发展以及环保意识的不断提高,一些研究者对炭质泥岩粗粒土的路用性能进行了研究[1-4],其成果在实际工程中得到应用。在对炭质泥岩粗粒土路堤边坡稳定性进行分析时,应特别注意水体入渗对炭质泥岩粗粒土路堤边坡稳定性的影响。水体入渗除了会引起炭质泥岩粗粒土孔隙水压力上升、重度增大及基质吸力减小外,还会软化炭质泥岩[5-6],弱化其力学参数,显著降低炭质泥岩路堤边坡的稳定性。一些研究人员分析了降雨入渗及水位升降过程中炭质泥岩粗粒土路堤边坡的稳定性变化规律,并对炭质泥岩土分层路堤的入渗规律及稳定性进行了研究[7-10],但对于炭质泥岩粗粒土路堤边坡的入渗深度与时间的动态关系的研究不够深入。
目前,国内外运用最广泛的入渗模型为Green-Ampt模型[11],该模型参数简单,物理意义明确,在多孔介质中的垂直入渗的研究中得到了广泛应用。但该模型在应用于边坡降雨入渗分析时存在以下不足:1)Green-Ampt模型假设表面水平,且存在一定的积水深度,而实际边坡则是表面倾斜,雨水除了渗入边坡内部之外,常在边坡表面形成径流,沿着坡面排走,难以形成积水,因此,边坡降雨入渗初期不一定存在饱和区;2)Green-Ampt模型假定湿润锋以内土体为完全饱和状态,不存在非饱和区,未考虑非饱和渗流,这与实际情况不符。
部分学者对该模型进行了改进,将其用于分析边坡降雨入渗情况。汪丁建等[12]在原模型的基础上考虑了沿坡面发生的渗流以及渗透力,但未分析土体湿润层的体积含水率沿深度的分布;BOUWER[13]对入渗进行了研究,建议湿润锋以内土壤导水率为饱和导水率的0.5倍;MA等[14]发现湿润锋以内土体导水率为饱和导水率与饱和系数之积;吕特等[15]建议对渗透系数进行修正,修正系数取0.7。以上研究虽然对渗透系数进行了修正,但仅适合某种特定土体或者入渗深度在一定范围内的情况,且未考虑渗透系数的动态变化。YAO等[16]考虑了饱和区与非饱和区厚度各占湿润锋深度的50%,并将其用于边坡稳定性分析。张洁等[17]研究了适用于斜坡降雨的Green-Ampt模型,但将渗透系数采用饱和渗透系数的一半,未考虑渗透系数随着湿润锋的推进而不断变化的情况。王文焰等[18-19]通过实验统计并验证了饱和层厚度约为湿润锋厚度的一半,但这种处理过于简单,未考虑随着湿润锋的推进,饱和层占湿润锋的比例会不断变大等情况。
由以上分析可知,当前对Green-Ampt 模型的改进主要集中在对渗透系数进行修正以及考虑湿润锋内饱和区和非饱和区的影响等方面。这些研究大多通过引入一些经验系数来进行改进,因此,计算结果存在较大主观性,无法动态考虑雨水入渗深度、湿润锋内饱和、非饱和区域及渗透系数的变化。为此,本文作者在前人的基础上,考虑降雨入渗过程中非饱和区对入渗量和渗透系数的影响,对Green-Ampt模型中的渗透系数和饱和非饱和区域分布情况进行修正;结合土体抗剪强度公式,分别以湿润锋面、饱和区与非饱和区的交界面为危险滑动面,将改进后的Green-Ampt 模型用于炭质泥岩路堤边坡稳定性分析,最后将改进前后的Green-Ampt模型计算结果与数值模拟结果进行对比,分析本文改进模型的可靠性,为工程实践提供参考。
1 入渗模型分析
1.1 Green-Ampt入渗模型
Green和Ampt研究土体在薄层积水时提出一种入渗模型即Green-Ampt 入渗模型,该模型假定:1)土体沿深度方向上的体积含水率始终不变;2)雨水入渗过程中湿润锋面始终为1个干湿截然分开的界面,即湿润锋内体积含水率为饱和含水率θs,湿润锋下方土体的体积含水率为初始含水率θi,如图1所示[11]。
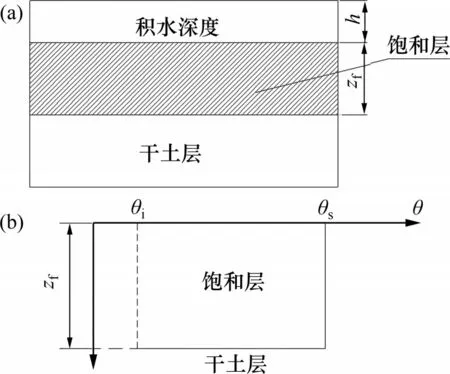
图1 Green-Ampt模型入渗图Fig.1 Infiltration diagram of Green-Ampt model
基于上述假设和达西定律,土体的入渗速率为
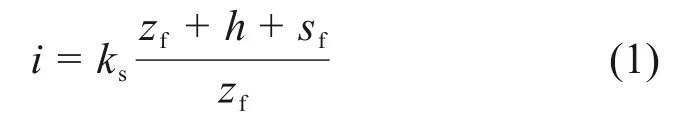
式中:i为入渗速率,m/d;h为地表积水深度,m;zf为湿润锋深度,m;ks为饱和渗透系数,m/d;sf为湿润锋处的平均基质吸力水头,m。
Green-Ampt模型假设湿润锋至入渗初始表面之间的土体达到完全饱和,故累计入渗量I为

式中:θs为饱和体积含水率;θi为初始体积含水率。
由累计入渗量I和入渗速率i的导数关系可得

联合式(1),(2)和(3),可得雨水入渗深度h和时间t的函数关系为
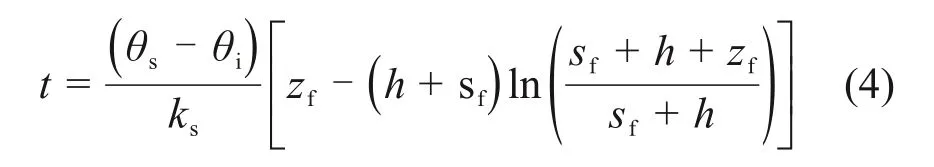
式(4)即为Green-Ampt 入渗模型。该公式形式简单,但未考虑非饱和区和渗透系数的变化,故其应用存在一定局限性。
1.2 改进的Green-Ampt入渗模型
本文在Green-Ampt 模型基础上,将雨水入渗分为2个阶段:降雨强度控制阶段和土体入渗能力控制阶段。
1.2.1 降雨强度控制阶段
在降雨强度控制阶段,假设土体仅表面层饱和,厚度忽略不计,湿润锋至边坡坡面全为非饱和区,此时,降雨全部渗入土体,随着降雨时间增加,非饱和区不断增大。采用椭圆形曲线来描述非饱和区的体积含水率沿深度的分布规律[19],水平半轴为饱和体积含水率和初始体积含水率之差,竖向半轴为非饱和区深度,第一阶段入渗模型示意图如图2所示。对于边坡而言,表面不发生积水,此阶段的极限状态为降雨强度等于土体入渗能力控制阶段时的初始入渗速率,即
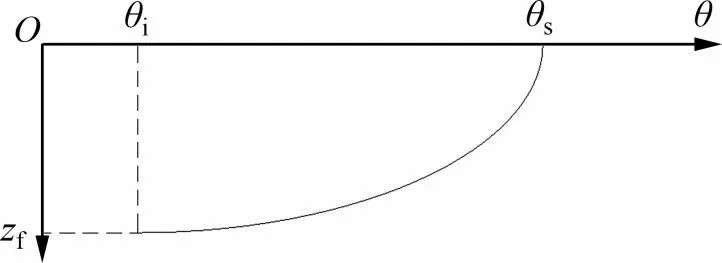
图2 第一阶段改进Green-Ampt 入渗模型示意图Fig.2 Schematic diagram of the first stage of the improved Green-Ampt infiltration model
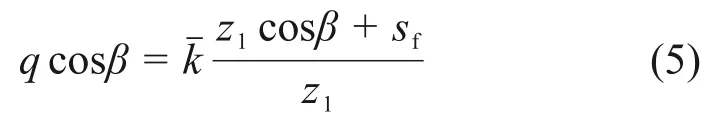
式中:q为降雨强度,m/d;β为边坡倾角,(°);z1为土体开始出现饱和区时的湿润锋深度,m;kˉ为非饱和区的等效导水率,m/d。
根据彭振阳等[20]的研究,非饱和区的入渗系数沿深度线性减小,其渗透系数为
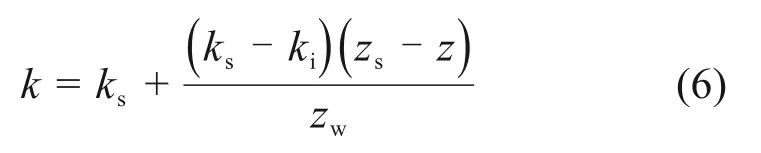
其中:zs为饱和区厚度,m;zw为非饱和区厚度,m;ki为干燥层的导水率,m/d。
非饱和区的等效导水系数k为

结合式(6)和式(7)以及饱和区深度zs可得湿润锋至边坡表面的等效导水系数:
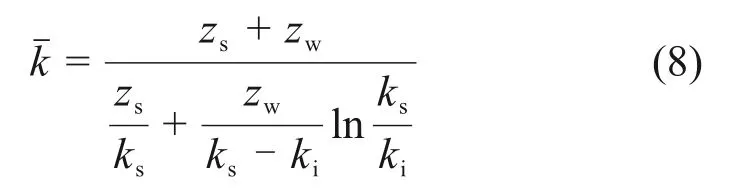
在第一阶段,zs=0,可得
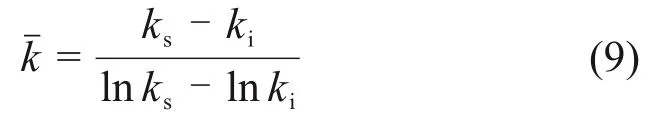
联立式(5)和(9)可得
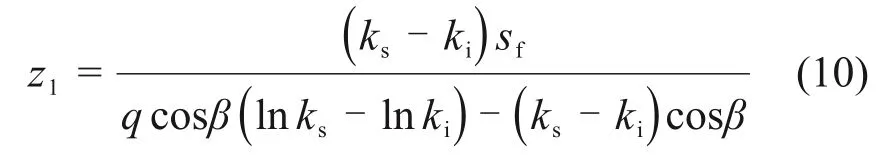
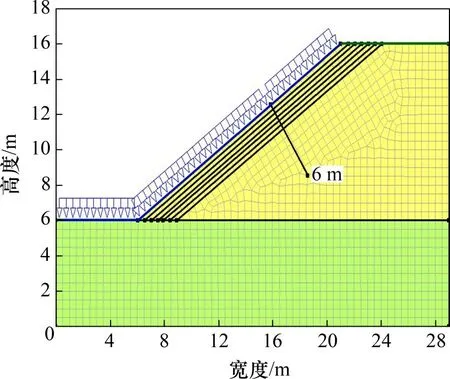
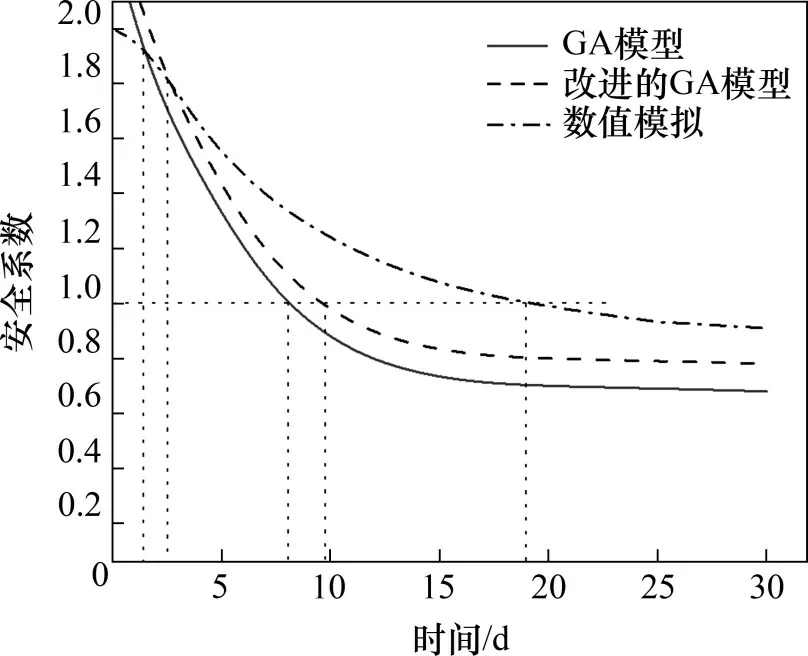
当zf 根据非饱和区体积含水率与深度的椭圆关系可得 由式(11)和式(12)可得降雨入渗后未出现饱和区时的Green-Ampt入渗模型为 将式(10)代入式(13)可得路堤开始出现饱和区时所对应的时间t1为 1.2.2 土体入渗能力控制阶段 当降雨时间t>t1时,雨水入渗进入第二个阶段即土体入渗能力控制阶段。在此阶段,降雨强度大于入渗速率,土体内部饱和区开始不断增大,非饱和区体积占湿润锋至边坡坡面之间的区域体积的比例不断减小。第二阶段入渗模型如图3所示。在第二阶段,随着湿润锋深度不断增大,土体饱和区开始扩大,非饱和区体积占湿润锋至边坡表面区域的体积的比例沿湿润锋深度线性减小[20],可得 图3 改进Green-Ampt入渗模型第二阶段示意图Fig.3 Schematic diagram of the second stage of the improved Green-Ampt infiltration model 其中:a和b为经验参数。 联立式(8)和式(15)可得 此时,入渗速率i为 累计入渗量I为 将式(18)代入式(3)有 将式(17)代入式(19)得 将式(20)积分后得到土体内部出现饱和区时的Green-Ampt入渗模型为 炭质泥岩粗粒土路堤边坡在降雨作用下容易发生浅层滑坡[21-22],破坏面多为湿润锋面。而本文将湿润锋至边坡表面的区域分为饱和区和非饱和区,饱和区与非饱和区的交界面也可能是危险滑动面[23-25]。采用取倾角为β的单位长度的边坡为研究对象,分别以湿润锋面、饱和区和非饱和区的交界面为危险滑动面(如图4所示),利用极限平衡法求出最不利条件下的边坡安全系数,分析边坡安全系数随雨水入渗深度和降雨时间的变化关系。 图4 不同阶段的边坡滑动面示意图Fig.4 Schematic diagrams of slope sliding surface at different stages 当以湿润锋面为危险滑动面进行分析时,抗滑力采用Fredlund非饱和土体的抗剪强度公式[26]求解;当以饱和区和非饱和区的交界面处为危险滑动面进行分析时,抗滑力采用摩尔-库仑饱和土体的抗剪强度公式求解。同时,考虑炭质泥岩粗粒土软化特性,随着饱水时间增加,对土体黏聚力和内摩擦角进行折减[4-5]。假设非饱和区土体重度与体积含水率呈线性相关,则土体重度沿非饱和区深度呈椭圆分布。非饱和区土体重度计算模型如图5所示,此时,不同体积含水率的单位土体重度γ可表述为 图5 非饱和区土条重度示意图Fig.5 Schematic diagram of soil strip weight in unsaturated zone 式中:γi和γs为初始重度和饱和重度,kN/m3。 非饱和区自重应力为 在降雨强度控制阶段中,当土体内仅有非饱和区时,非饱和区厚度zw即为湿润锋深度zf,此时,边坡安全系数Fs为 在土体入渗能力控制阶段中,当土体内同时存在非饱和区及饱和区时,分别计算不同交界面的安全系数。以饱和区和非饱和区的交界面为滑动面时的边坡安全系数Fs1可表示为 其中:σn=γszs;τm=γszstanβ;zs为饱和区深度,m;c″为考虑浸水软化后的有效黏聚力,kPa;φ″为考虑浸水软化后的有效内摩擦角,(°)。 以湿润锋面为滑动面时的边坡安全系数Fs2为 取Fs1与Fs2两者的较小值为土体入渗能力控制阶段的边坡安全系数。 为对比Green-Ampt 模型、改进Green-Ampt 模型对某炭质泥岩粗粒土路堤边坡在降雨条件下的湿润锋和边坡稳定性动态变化规律,采用Geo-studio建立数值模型。模型采用seep/w 模块进行渗流计算,应用Morgenstern-Price法对不同降雨时间下的边坡稳定性进行分析。 该数值计算模型宽为29 m,高为16 m,路堤边坡高为10 m,坡度为1.0:1.5;根据路堤所在地区,选取降雨强度为0.04 m/d。路堤填料力学参数和渗流特性参数如表1和表2所示。为考虑炭质泥岩的软化效应,本文在路堤稳定性分析过程中,基于入渗模拟的结果、边坡土层的饱水时间和饱和区深度,对炭质泥岩强度进行折减[4-5,26],数值计算模型如图6所示,单元数为1 489个,节点数为1 415个。边坡坡面设置为降雨边界,边坡底部和两侧设置为不透水边界。同时,将边坡表面设置为潜在渗流面,边坡表面阴影线部分为强度折减区域,根据入渗深度和饱和时间对该层土体进行强度折减,边坡表面垂直边坡的黑色直线为入渗深度监测曲线。 表1 炭质泥岩粗粒土物理力学参数Table 1 Physical and mechanical parameters of carbonaceous mudstone coarse-grained soil 表2 炭质泥岩粗粒土渗流特性参数Table 2 seepage characteristics parameters of carbonaceous mudstone coarse-grained soil 图6 数值计算模型Fig.6 Numerical calculation model Green-Ampt 模型、改进Green-Ampt 模型以及边坡降雨入渗数值模拟中的入渗深度(湿润锋深度)和时间的关系如图7所示。从图7可以看出:改进的Green-Ampt 模型得到的入渗深度处于Green-Ampt 模型计算结果与数值模拟计算结果之间;当降雨时间较短(t<1 d)时,改进前后的Green-Ampt模型和数值分析模型计算得到的湿润锋深度相差较小,而随着降雨时间逐渐增加,这3种方法计算的湿润锋深度差值开始增加;当降雨时间为15 d时,数值计算得到的湿润锋深度比改进Green-Ampt 模型所得到湿润锋深度大0.57 m 左右;当降雨时间增加到30 d时,两者差值增大到0.76 m,之后差值并基本趋于稳定;而Green-Ampt 模型计算的湿润锋深度与改进后的Green-Ampt 模型和数值模拟计算得到的湿润锋深度的差值不断扩大;改进后的Green-Ampt 模型与数值模拟得到的湿润锋推进速率(即图7中各曲线斜率)随着降雨时间增加而逐渐减小,最后基本相同,这是因为入渗速率与渗透系数和水力梯度有关,改进后的Green-Ampt 模型与数值模拟考虑了倾角对水力梯度、非饱和区对渗透系数的影响,而Green-Ampt 模型得到的入渗速率较大。 图7 湿润锋深度与时间的关系Fig.7 Relationship between depth of wet front and time Green-Ampt 模型、改进Green-Ampt 模型以及数值分析中边坡安全系数随降雨入渗时间t的变化关系如图8所示。从图8可以看出:随着降雨时间t增加,这3 种方法计算的安全系数均不断降低;Green-Ampt 模型、改进的Green-Ampt 模型与数值模拟所计算的安全系数分别在t=1.5 d附近和t=2.5 d附近相交;当降雨时间小于10 d 时,改进前后的Green-Ampt模型所计算的安全系数随降雨时间增加而迅速降低,而数值模拟计算安全系数则在t=2.0 d之前先缓慢降低之后迅速下降;当降雨时间大于10 d 时,这3 种方法计算的边坡安全系数均趋于稳定。 图8 边坡安全系数与时间的关系Fig.8 Relationship between slope safety factor of wet front and time 随着降雨时间增加,Green-Ampt模型所得安全系数最先降至1.0以下,而后是改进的Green-Ampt模型,最后是数值模拟,最终Green-Ampt 模型、改进的Green-Ampt 模型和数值模拟所得安全系数分别稳定在0.68,0.78和0.89附近,前者比后两者分别低0.10和0.21,且改进的Green-Ampt模型计算得到的安全系数始终高于Green-Ampt 模型计算得到的安全系数。 从上述分析可得改进的Green-Ampt 可以应用于边坡稳定分析,相应步骤为:1)确定降雨强度以及边坡初始含水率;2)根据改进的Green-Ampt 模型估算不同入渗时间对应的入渗深度;3)根据边坡稳定性计算方法得到相应深度下的安全系数;4)根据时间、深度的对应关系得到降雨时间下的边坡安全系数。 1)改进的Green-Ampt 模型得到的入渗深度小于Green-Ampt 模型的计算结果而大于数值模拟计算结果,且随着降雨时长增加,由改进的Green-Ampt 模型所得入渗深度与数值模拟计算的入渗深度差值趋于稳定,稳定在0.76 m左右。 2)在湿润锋深度和时间的关系曲线中,三者的湿润锋推进速率不断减小,慢慢趋于稳定;改进的Green-Ampt模型和数值模拟得到的湿润锋推进速率较一致。 3)随着降雨入渗时间不断增大,不同方法计算的边坡安全系数不断减小,最终均趋于稳定。改进的Green-Ampt模型得到的边坡安全系数介于Green-Ampt 模型计算结果和数值模拟计算结果之间。初始模型比改进之后的模型和数值模拟得到的边坡安全系数最终分别低0.10和0.21。




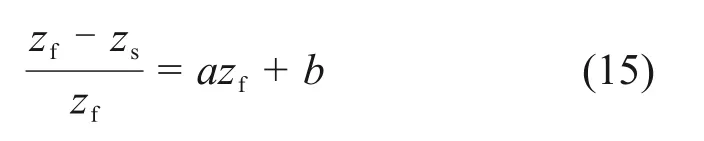


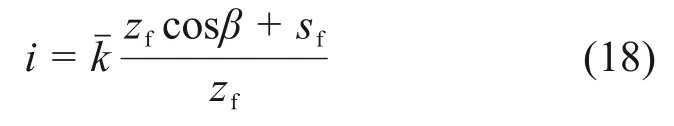
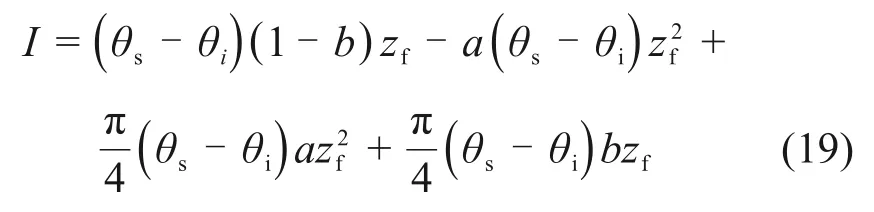
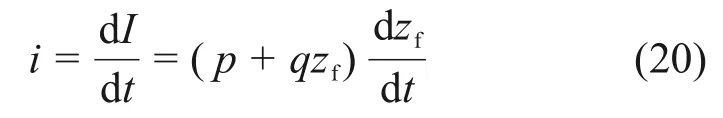
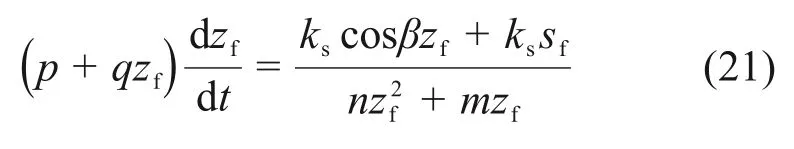

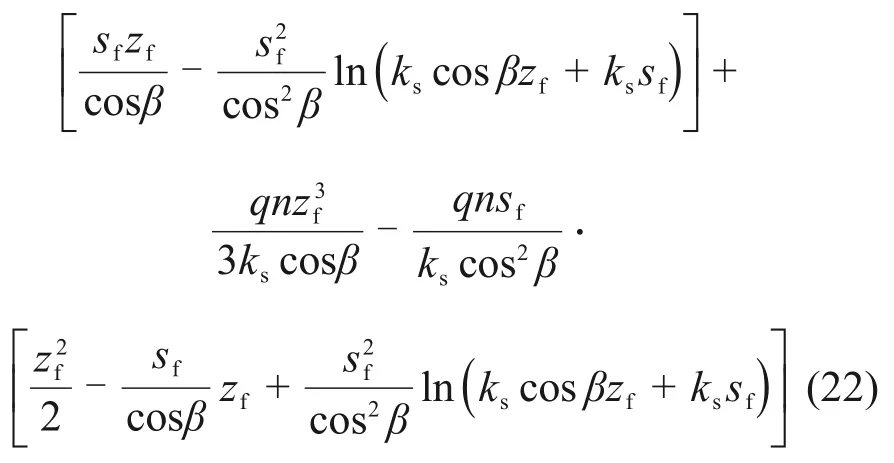
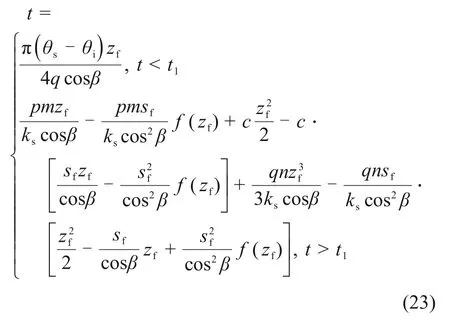
2 边坡稳定性分析
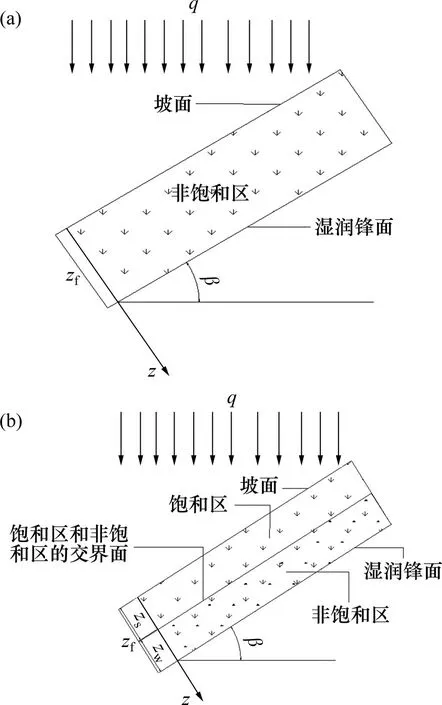

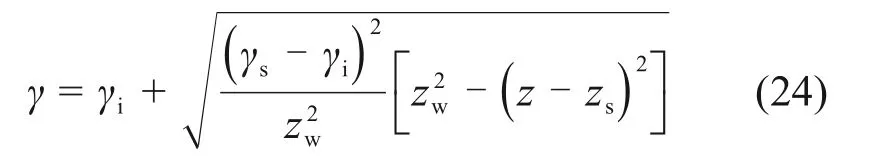
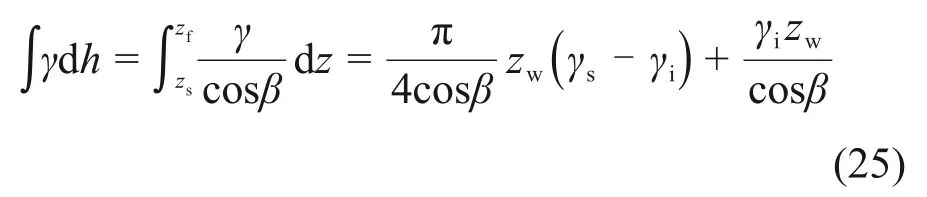
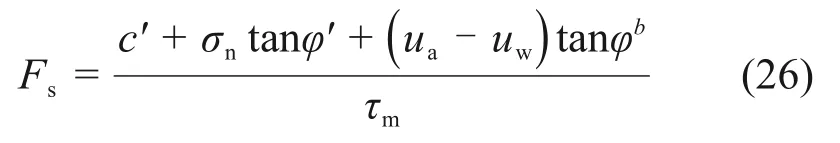
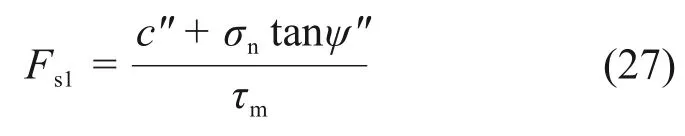
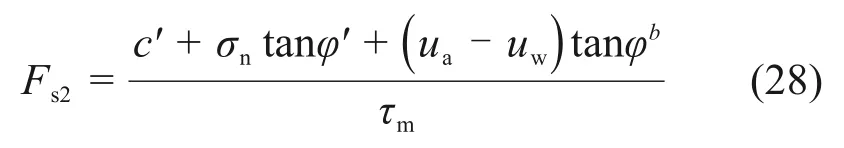
3 数值模拟


4 结果分析

5 结论

