Global Practical Stabilization of Discrete-Time Switched Affine Systems via a General Quadratic Lyapunov Function and a Decentralized Ellipsoid
Mohammad Hejri,
Abstract—This paper addresses the problem of global practical stabilization of discrete-time switched affine systems via statedependent switching rules.Several attempts have been made to solve this problem via different types of a common quadratic Lyapunov function and an ellipsoid.These classical results require either the quadratic Lyapunov function or the employed ellipsoid to be of the centralized type.In some cases,the ellipsoids are defined dependently as the level sets of a decentralized Lyapunov function.In this paper,we extend the existing results by the simultaneous use of a general decentralized Lyapunov function and a decentralized ellipsoid parameterized independently.The proposed conditions provide less conservative results than existing works in the sense of the ultimate invariant set of attraction size.Two different approaches are proposed to extract the ultimate invariant set of attraction with a minimum size,i.e.,a purely numerical method and a numerical-analytical one.In the former,both invariant and attractiveness conditions are imposed to extract the final set of matrix inequalities.The latter is established on a principle that the attractiveness of a set implies its invariance.Thus,the stability conditions are derived based on only the attractiveness property as a set of matrix inequalities with a smaller dimension.Illustrative examples are presented to prove the satisfactory operation of the proposed stabilization methods.
I.INTRODUCTION
SWITCHED systems are an important subclass of hybrid dynamical systems consisting of a family of continuousvariable subsystems and a switching law that determines which subsystem should be activated at each instant of the time [1].One of the most important subclasses of switched systems is theswitched affine systemsthat are very common in practice,especially in switching power converters [2]–[8].In this class of switched systems,there is not any common equilibrium point among all subsystems.Instead,the equilibrium point varies discontinuously during switching among subsystems,and therefore,to achieveasymptotic stabilityin a desired equilibrium point,the switching frequency should approach infinity,which is not realizable in practice [9]–[11].To handle chattering problems,one can use space or time regularization techniques.The former enforces a dwell-time using space-based hysteresis logic,and the latter utilizes an explicit timer preventing switching up to a guaranteed dwell-time [11]–[14].In either case,due to the limitation on the switching frequency and non-existence of a common equilibrium point among subsystems,stability with respect to a set rather than a particular point can be achieved.In this regard,the notion ofpractical stabilityhas been proposed in the literature to analyze switched systems'stability without any common equilibria [15]–[17].
It should be noted that the practical stability and stability in the sense of Lyapunov are distinct concepts,and neither implies the other.The states of a system may oscillate around an equilibrium point with sufficiently small deviations,although the system may be mathematically unstable.Such a situation may be quite tolerable in the sense of practical stability,and its performance is acceptable in practice,while the system is still Lyapunov unstable [18],[19].In this regard,compared to the classical Lyapunov stability analysis of the switched linear and nonlinear systems with a common equilibrium point,there has been little work on the practical stability analysis and stabilization of the discrete-time switched affine systems via state-dependent switching rules.The reader is referred to [20] and [21] for surveys of recent developments on the practical stability and stabilization of switched systems without common equilibria.
Previous works on the global practical stabilization of the switched affine systems via state-dependent switching rules require either the quadratic Lyapunov function or the employed ellipsoid to be of the centralized type.Among them,the stabilization techniques in [11],[16],[17],[20]–[22]utilize a centralized Lyapunov function and a centralized ellipsoid.In [9],a decentralized Lyapunov function and a centralized ellipsoid are used for controller design and practical stability analysis.The works in [10],[23] employ a centralized Lyapunov function and decentralized ellipsoid.In some cases,such as [24],although shifted Lyapunov functions and ellipsoids are used,the invariant set of attraction is considered,as the level sets of the Lyapunov function and is not parameterized independently.
In this regard,the main objectives and contributions of the paper are summarized as follows.First,new sufficient conditions are provided for the global practical stabilization of discrete-time switched affine systems in a fully decentralized setting by the simultaneous use of a common decentralized quadratic Lyapunov function and a decentralized ellipsoid parameterized independently.Second,a numerical-analytical method is proposed to estimate the invariant set of attraction size.The main purpose in this part is to achieve a set of matrix inequalities with smaller dimensions that may be numerically tractable compared to the existing purely numerical methods.Third,a multiobjective optimization problem is proposed by which the invariant set of attraction size and the steady-state errors of the system trajectories are minimized simultaneously.Finally,the controller design procedure is developed such that the Lyapunov function does not require positive definiteness in the whole state-space but outside of a decentralized ellipsoid.The preceding features imply that the present work's proposed conditions are less restrictive than those in existing works.
The remainder of the paper is organized as follows.Section II provides the practical stabilization of discrete-time switched affine systems via state-dependent switching rules.Some basic definitions of the various types of practical stability are presented in this section.Section III provides the stabilization strategy in a pure numerical setting,including state-dependent switching rules and stability conditions,as a set of matrix inequalities.A numerical-analytical stabilization method with a possibility of a unified switching rule in the whole state space is established in Section IV.Section V formulates the optimization problems corresponding to stability conditions to minimize the size of the invariant set of attraction and steadystate errors.Section VI illustrates the theoretical results via two examples:one academic example and a DC-DC stepdown switching converter.Finally,concluding remarks are made in Section VII.
Notations:R,R≥0,Z≥0are used to denote the set of real,nonnegative real,and nonnegative integer numbers,respectively.Rnand Rm×ndenote real-valued n-dimensional column vectors andm×nmatrices,respectively.We useInand 0nto denote then×nidentity matrix and then×1 zero vector,respectively.For matrixM∈Rm×n,MTdenotes its transpose,and for a square matrixM∈Rn×n,M−1,tr(M),and λi(M)are inverse,trace,andith eigenvalue ofM,respectively.Moreover,λmax(M) and λmin(M)are used to denote the largest and smallest eigenvalue ofM,respectively.Forx∈Rn,∥x∥denotes the Euclidean vector norm,i.e.,∥x∥=(xT x)1/2.M≺0 andM0 denote thatMis a negative definite and negative semi-definite matrix,respectively.For the set I,|I| denotes its number of elements (cardinality).In symmetric matrices,∗denotes each of their symmetric blocks.Assume that the set K={1,...,N}is a collection of theNfirst positive integer numbers,where the convex combination of matrices{M1,...,MN} is denoted byMλ=∑i∈KλiMiwith λ∈Λ where Λ:={λ∈RN|λi≥0,∑i∈Kλi=1}is the unitary simplex.
II.PROBLEM STATEMENT AND PRELIMINARIES
We consider the discrete-time switched affine system as

wherek∈Z≥0is the discrete-time instant,x(k)∈Rnis the state and σ(x(k)):Rn→K is a state-dependent switching function that selects one of theNavailable subsystems (Ai,bi),i∈K at any instant of timek∈Z≥0.It is intended to design the statedependent switching function σ(x(k))such that to imposefinite time convergenceof the state trajectoriesx(k),k∈Z≥0,to aneighborhoodof a desired equilibrium point,for all initial conditionsx0∈Rn.In general,such an equilibrium point does not coincide with any other isolated subsystems,namely,xei=(In−Ai)−1bi.In some literature [2],[9],[11],[25]–[27]based on the common Lyapunov function,it is assumed that this point belongs to a specific set of attainable equilibrium points.For instance,in [9] this set is defined asXe={xe∈Rn|xe=(In−Aλ)−1bλ,λ∈S} withS⊆Λ such thatAλis Schur stable.In the present paper,a desired equilibrium pointxe∉Xemay be chosen.This free choice of equilibrium point may extend the application domain of the proposed stabilization technique.More specifically,the situation occurs when the stabilization of the switched affine systems is considered under uncertainty.In this case,the equilibrium pointxewill be a function of the system matrices’ unknown parameters and may not belong to the setXeextracted using the nominal system matrices without uncertainties.Given an equilibrium pointxe,we can always reformulate the stabilization problem around the null equilibrium point with defining the error state vectore(k)=x(k)−xe,∀k∈Z≥0that obeys the error dynamics as
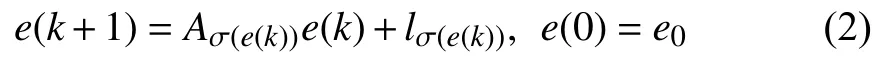
with σ(e(k))=σ(x(k)−xe),li=(Ai−In)xe+bi,∀i∈K.We plan to design the state-dependent switching function σ(e(k))via a general quadratic Lyapunov function candidatev(e)such that the decentralized ellipsoid E(Q,c,ρ)be an invariant set of attraction for the switched affine system (2)based on the following definitions.
We consider the general quadratic Lyapunov function
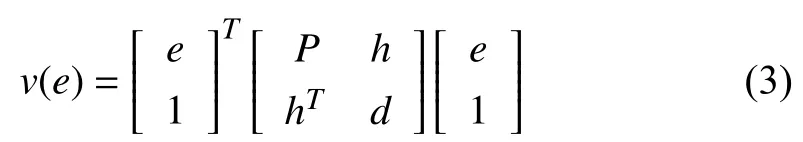
whereh∈Rn,P=PT∈Rn×n,andd∈R.The decentralized ellipsoid E (Q,c,ρ)is given by

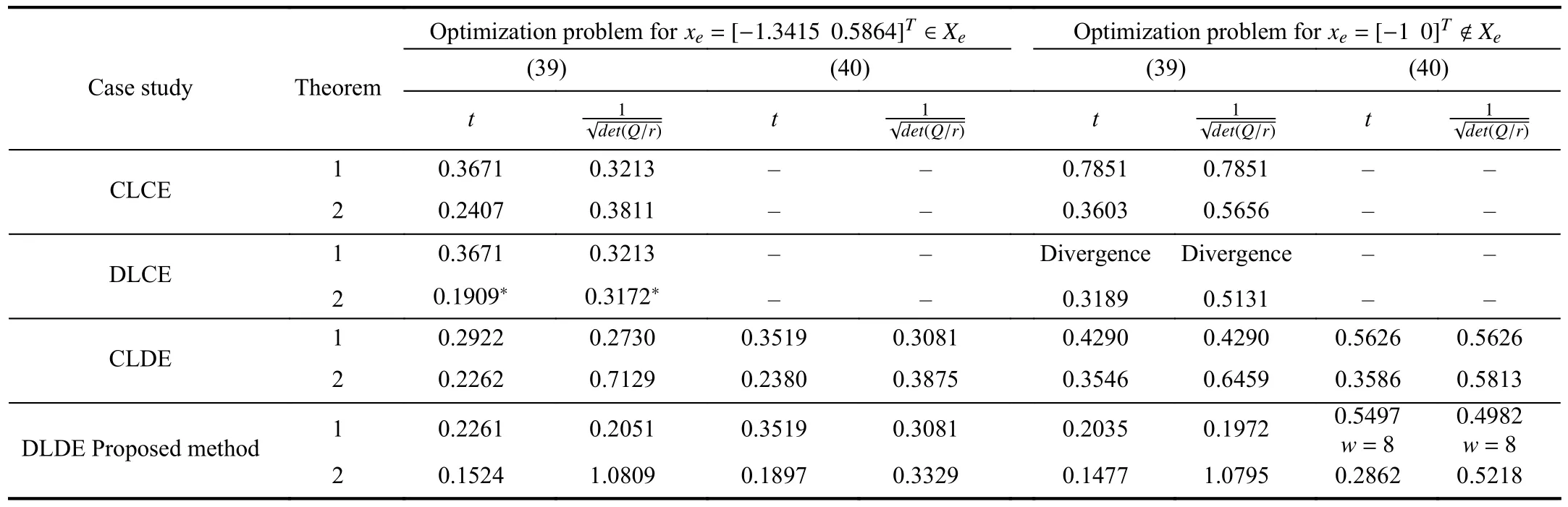
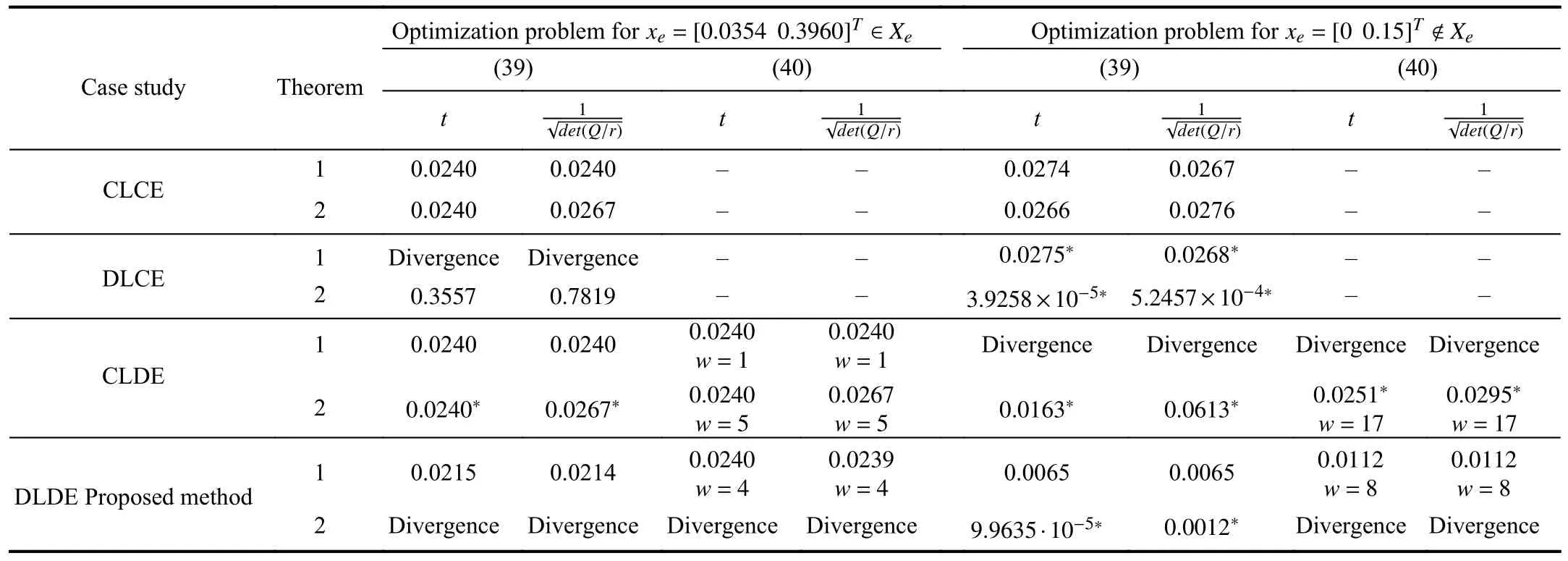
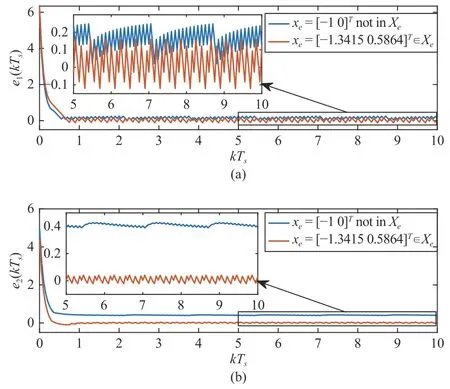
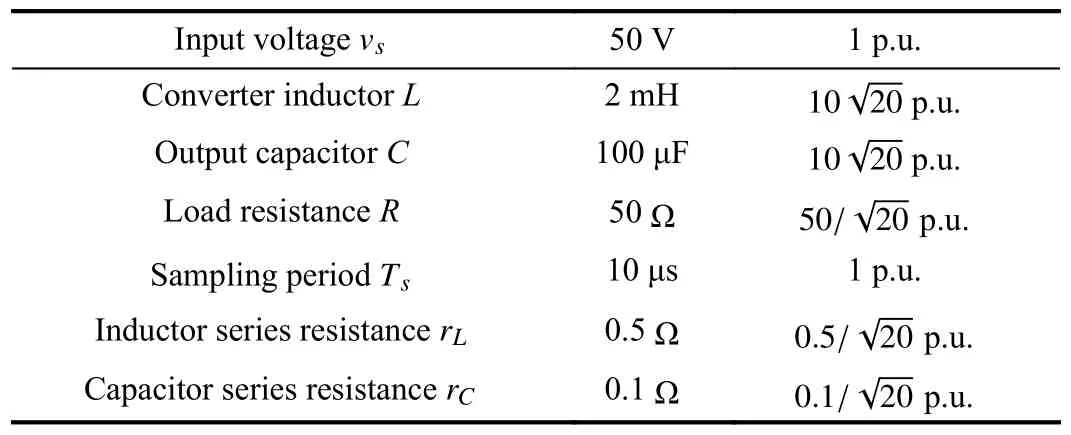
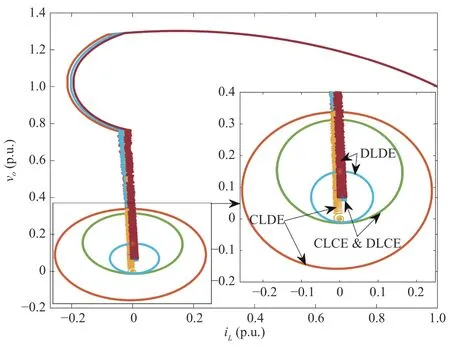
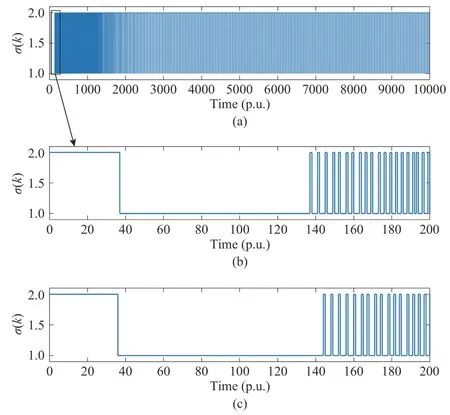
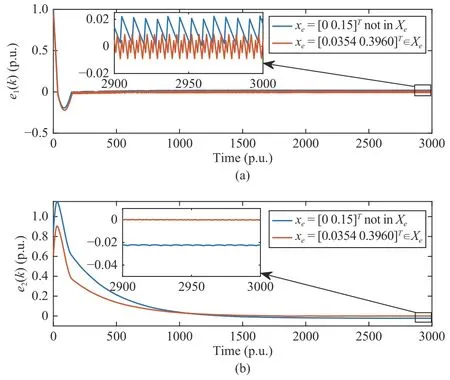
whereQ=QT≻0,c∈Rnand ρ∈R such that ρ wherer=cT Q−1c−ρ andec=−Q−1cis the center of the ellipsoid.In this paper,we taker=1 yielding ρ=cT Q−1c−1.Note that by ρ=cT Q−1c−1,the constraintρ Definition 1 (Invariant Set):An ellipsoid E(Q,c,ρ)in (4)is an invariant set on a given domainD⊂Rnfor the system (2)by the switching function σ(e(k))if the following conditions are simultaneously satisfied: a)0n∈E(Q,c,ρ) b)Ife(k0)∈E(Q,c,ρ),k0∈Z≥0,thene(k)∈E(Q,c,ρ),∀k≥k0,wherek∈Z≥0. According to (4),to satisfy condition (a)in Definition 1,it is necessary to have Definition 1 is a modified version of the available definition of the invariant set in the literature [28]–[30] in the sense that the condition a)and a decentralized ellipsoid are considered in our definition.These modifications result in an analogy between the set invariance and local practical stability definitions in the literature [15]–[18].Indeed,based on condition b),the trajectories starting within E(Q,c,ρ),never escape from it.Therefore,according to a),they will remain around the null set point. Definition 2 (Attractive Set):An ellipsoid E(Q,c,ρ)⊆Din(4)is said to be an attractive set on a given domainD⊂Rnfor the system (2)by the switching function σ(e(k))if the following conditions are simultaneously satisfied. a)0n∈E(Q,c,ρ) b)Ife(0)∈D−E(Q,c,ρ) then there is aT=T(e(0))≥0 such thate(k)∈E(Q,c,ρ),∀k≥T. According to (8),condition a)in Definition 2 is automatically satisfied. Definition 3 (Invariant Set of Attraction):An ellipsoid E(Q,c,ρ)⊆Dis an invariant set of attraction on a given domainD⊂Rnfor the system (2)by the switching function σ(e(k))if it is both invariant and attractive based on Definitions 1 and 2. It should be noted that the notion of the set attractiveness in Definition 2 is a bit different from those available in the literature.In [9],[24],[28]–[30],a setMis said to be an attractive set for the system (2)if any solutione(k) of (2)starting frome(0)∉Mapproaches setMwhenkapproaches infinity,i.e., wheredist(e(k),M)=infρ∈M∥ρ−e(k)∥.According to [15]–[18],the asymptotic practical stability of setMimplies that for the state trajectories starting outsideM,there is a finite timeT>0 such that the trajectorye(k)is ultimately insideM.However,the existing definition of set attractiveness in (9)does not imply such a property.It only guarantees that the distance between the state trajectorye(k)and setMapproaches zero without ensuring thate(k)entersMeventually.On the other hand,Definition 2 falls into the context of practical stability where the trajectories enter the ellipsoid E(Q,c,ρ)in a finite time.Definitions 4–6 clarify these notions. Definition 4:System (2)is locally practically stable with respect to an ellipsoid E(Q,c,ρ)⊆Don the domainD⊂Rnunder switching function σ(e(k)) if the ellipsoid E(Q,c,ρ)is an invariant set based on Definition 1. Definition 5:System (2)is practically asymptotically stable in the large with respect to an ellipsoid E(Q,c,ρ)⊂Don the domainD⊂Rnunder switching function σ(e(k))if the ellipsoid E(Q,c,ρ)is an invariant set of attraction based on Definition 3. Definition 6:System (2)is practically asymptotically stable in the whole or globally practically asymptotically stable if it is practically asymptotically stable in the large andD=Rn. Definition 7:In Definitions 3–6,the setD−E(Q,c,ρ)is called the domain of attraction of the system (2)under switching rule σ(e(k)). The ellipsoid E(Q,c,ρ)in Definitions 4–7 is given by (4)and can be replaced by its equivalent form (5).Lemma 1 states the conditions where the autonomous switched nonlinear system (10)ispractically asymptotically stable in the largein the sense of Definition 5. where σ(e(k))∈K is the switching function.We do not require 0n=fi(0n),∀i∈K.It is also assumed that the vector fieldsfisatisfy suitable conditions guaranteeing the existence and uniqueness of solutions of (10)starting anye(0)∈Dand∀k∈Z≥0.The switched affine system (2)is a special case of the nonlinear switched system in (10).Moreover,it should be noted that the Definitions 1–6 are valid for the system (10). Lemma 1:System (10)is practically asymptotically stable in the large in a given domainD⊂Rncontaining the origin in the sense of Definition 5 if there exists an ellipsoid E(Q,c,ρ)⊂Dwith (8),a scalar functionv(e(k)):Rn→R and a switching rule σ(e(k))such that a)Ife(k)∈E(Q,c,ρ) thene(k+1)=fσ(e(k))(e(k))∈E(Q,c,ρ). b)Ife(k)∈D−E(Q,c,ρ) thenv(e(k+1))−v(e(k))=∆v(e(k))≤−γ<0 where γ >0. c)v(e(k))is positive definite inD−E(Q,c,ρ),i.e.,v(e(k))>0 whene(k)∈D−E(Q,c,ρ). Proof:Condition a)is the same as condition b)of Definition 1.Moreover,from (4)and (8),one can conclude 0n∈E(Q,c,ρ),and therefore,condition a)of Definitions 1 and 2 is satisfied.Thus,the invariant property of ellipsoid E(Q,c,ρ)is concluded.To prove the attractive property of the set E(Q,c,ρ),according to condition b)of Definition 2,it is necessary to show that starting any initial statee(0)∈D−E(Q,c,ρ),∃T=T(e(0))>0 such thate(k)∈E(Q,c,ρ)fork≥T.We show this by contradiction as follows.Assume that the state trajectorye(k) never intersects E(Q,c,ρ).Then at any instantkoutside E(Q,c,ρ)and according to condition b),we havev(e(k+1))−v(e(k))≤−γ<0.Thus,one can write The right side of (11)will eventually be negative whenktakes large values.This leads to a contradiction to the condition c)where it is assumedv(e(k))is positive definite onD−E(Q,c,ρ).As a result,the state trajectorye(k)will eventually enter inside the ellipsoid E(Q,c,ρ)in finite timeT,and due to the condition a),remains within it ∀k≥T.Therefore,E(Q,c,ρ)is an invariant set of attraction according to Definition 3,and as a result,according to Definition 5,system (10)is practically asymptotically stable in the large on the domainDand under the switching function σ(e(k)). ■ Using (11),one can obtain an upper bound of the reaching time asT=T(e(0))≤. Remark 1:In Lemma 1,ifD=Rn,then according to Definition 6,system (2)is globally practically asymptotically stable. In this section,the stabilization procedure based on a pure numerical setting is presented.As discussed in Section II,we are planning to design a switching rule σ(e(k))via a general quadratic Lyapunov function (3)for the system (2)to make it globally practically asymptotically stable.Proposition 1 provides sufficient conditions under which the ellipsoid E(Q,c,ρ)is an invariant set for the system (2)under switching rule (12)in the sense of Definition 1. Proposition 1:If there exist matrixQ=QT≻0,vectorsh,c∈Rn,scalarsd∈R,ρ≤0,nonnegative numbers τ1≥0,λ1i≥0,i∈K,satisfying the system of inequalities where then the switching strategy in (12)assures that the ellipsoid E(Q,c,ρ)in (4)is an invariant set for discrete-time switched affine system in (2)in the sense of Definition 1. Proof:Please see the Appendix. ■ To obtain the attractiveness property,we introduce the mintype state-feedback switching function as Proposition 2 provides sufficient conditions that make ellipsoid E(Q,c,ρ)in (4)anattractive setfor the switched affine system (2)under switching function (18)in the sense of Definition 2. Proposition 2:If there exist matricesQ=QT≻0,P=PT∈Rn×n,vectorsh,c∈Rn,constantsd∈R,ρ≤0,and nonnegative numbers λ2i≥0,i∈K,τ2,τ3≥0 satisfying the system of inequalities where then the switching strategy in (18)assures that the ellipsoid E(Q,c,ρ)in (4)is an attractive set for the system (2)on the domainD=Rnin the sense of Definition 3. Proof:Please see the Appendix. ■ Condition (19)in Proposition 2 implies the existence of a Schur stable convex combination of subsystems matrices.The proof of this statement is similar to the proof of Corollary 1 in [21] and is omitted here.Using Propositions 1 and 2,one can conclude the following result. Theorem 1:If there exist matricesPT=P,QT=Q≻0,vectorsh,c,l∈Rn,scalarsd∈R,ρ≤0,and nonnegative numbers τ1,τ2,τ3≥0,λ1i,λ2i≥0,i∈K satisfying the system of inequalities (19)–(21),(13)–(14)and (6)–(7)then,based on Definition 3,the ellipsoid E(Q,c,ρ)in (4)is an invariant set of attraction for system (2)under switching rule (12)whene(k)∈E(Q,c,ρ)and switching rule (18)whene(k)∉E(Q,c,ρ).As a result,system (2)is globally practically asymptotically stable in the sense of Definition 6. Theorem 1 is theoretically appealing and provides a singlestage design procedure compared with the double-stage design methods in [9],[10].Assuming that there is a global optimization tool,the optimal design of the parameters with the proposed conditions in Theorem 1 is performed by onetime implementation of the optimization software.On the other hand,in the double-stage design method,the optimization tool should be implemented many times between two stages to cover the whole search space of the decision variables and obtain the ultimate global optimal solution.Moreover,according to (21),the positiveness of the Lyapunov function in (3)is required only outside ellipsoids (4)or (5),while in [9],[10],it is assumed that the Lyapunov function is positive in the whole state space.Therefore,the proposed conditions in Theorem 1 may be less restrictive than those proposed in [9],[10],and offer some advantages from the optimization of parameters and implementation point of views.However,from a numerical point of view,similar to the proposed conditions in [9],[10],the conditions of Theorem 1 are of BMI type and,therefore,are computationally intractable. In this regard,in the sequel,we present another method that may be more numerically tractable.In this method,only the attractiveness conditions proposed in Proposition 2 are solved numerically.Next,the ultimate invariant set of attraction is calculated analytically via Proposition 4. During the numerical experiments in Section VI,we observed that in most cases,the ellipsoid E(Q,ec,1)in (5)is not only attractive by the switching rule (18)but also by the switching law in (12).Such a possibility is of particular importance from several aspects.First,instead of using two different switching rules,i.e.,(12)inside of the ellipsoid and(18)outside of it,one can use a unified controller (12)in the whole state space.As a result,the controller logic is simplified,and it can be implemented more easily.Second,in some cases,due to numerical issues,the switching rule (18)does not result in convergence.However,the execution of(12)is successful.Finally,achieving the attractiveness property via switching rule (12)provides a possibility to estimate the invariant set of attraction in a numericalanalytical setting based on only attractiveness conditions in Proposition 2.As a result,without considering the invariant conditions of Proposition 4,the stability conditions of Theorem 2 are developed via matrix inequalities in a smaller dimension,which may be more numerically tractable.This section provides the theoretical basis for the preceding possibilities. The next lemma provides a sufficient condition for the attractiveness of the ellipsoid E(Q,c,ρ)in (4)based on the switching rule (12)rather than (18). Lemma 2:Ellipsoid E(Q,c,ρ) withQ=QT≻0 and (8)is an attractive set for the system (2)according to Definition 2 and using switching function (12)if ∀e(k)∉E(Q,c,ρ),∃i∈K such that Proof:Please see the Appendix. ■ Based on Lemma 2 and using the equivalency relation between the ellipsoid representations in (4)and (5),one can conclude the following results. Lemma 3:Let the conditions (6)–(7)be held.The switching rule in (12)is equivalent to the switching rule in Lemma 4:Let the conditions (6)–(8)be held.Ellipsoid E(Q,ec,1)in (5)withQ=QT≻0 is an attractive set for the system (2)according to Definition 2 and using switching function (12)if ∀e(k)∉E(Q,ec,1),∃i∈K such that Proposition 3 provides sufficient conditions under which the attractiveness conditions of Proposition 2 with the switching rule (18)imply the attractiveness property via switching law(12). Proposition 3:Consider matricesP=PTandQ=QT≻0,vectorsh,c∈Rn,constantsd∈R,ρ≤0 that follow from a feasible solution of Proposition 2.If there exist nonnegative constants≥0 and≥0 satisfying the system of inequalities where then the switching strategy in (12)assures that the ellipsoid E(Q,c,ρ)in (4)is an attractive set for discrete-time switched affine system in (2)in the sense of Definition 2. Proof:We show that the conditions of Proposition 3 imply the condition of Lemma 2.Pre-multiplying (27)by [e(k)T1]and post-multiplying it by [e(k)T1]Tand using S-procedure,one can obtain Now using (28)and (33),we have The expression in (34)is identical to the condition of Lemma 2,and as a result,the attractiveness of the ellipsoid E(Q,c,ρ)is concluded under switching rule (12). ■ It should be noted that given matricesP,Q,vectorsh,c,and constantsd,ρ by Proposition 2,the matrix inequalities in Proposition 3 are of the pure LMI type,and therefore,are numerically tractable. In Theorem 1,the global practical asymptotic stability of the system (2)is achieved via two different switching rules,i.e.,(12)inside of the ellipsoid E(Q,c,ρ)and (18)outside of it.If the LMI conditions of Proposition 3 are feasible,then one can use switching rule (12)instead of (18)in this theorem.With this approach,the global practical asymptotic stability of the system (2)is achieved via the unified switching rule (12)in the whole state space. Proposition 4 states that the existence of an attractive ellipsoid implies the existence of an invariant set of attraction. Proposition 4:Let the conditions (6)–(8)be held,and the ellipsoid E(Q,ec,1)in (5)be an attractive set for the system(2)according to Definition 2.SetRandR∗to be Then the following statements hold. a)IfR≤1,then E(Q,ec,1)is an invariant set of attraction for the system (2)independent of any switching strategy within E(Q,ec,1). b)IfR>1 andR∗≤1,then E(Q,ec,1)is an invariant set of attraction for the system (2)under switching rule (12)within E(Q,ec,1). c)Let the LMI conditions in Proposition 3 be satisfied.IfR∗>1,then the ellipsoid E(Q,ec,R∗)in (5)is an invariant set of attraction for system (2)under switching strategy (12)within E(Q,ec,R∗). Proof:Please see the Appendix. ■ It should be noted that the feasibility requirements of Proposition 3 imposed in item c)of Proposition 4,are not required in items a)and b)whereR≤1 andR∗≤1,respectively.On the other hand,the numerical examples show that the caseR∗>1 occurs more frequently,and fortunately,the feasibility requirements of Proposition 3 are satisfied in most cases. Theorem 2 states that one can infer the global practical asymptotic stability of the system (2)whenever anattractive setis provided through conditions of Propositions 2 and 3. Theorem 2:Assume that there exist matricesPT=P∈Rn×n,QT=Q≻0,i∈K,vectorsh,c,l∈Rn,scalarsd∈R,ρ≤0 nonnegative numbers τ2,τ3≥0,satisfying the system of inequalities (19)–(21)and (6)–(7).LetRandR∗be given by(35)and (36),respectively.Then the following statements hold: a)The ellipsoid E(Q,ec,1)in (5)withR≤1 is an invariant set of attraction for the system (2)under switching rule (18)whene(k)∉E(Q,ec,1).Thus,system (2)is globally practically asymptotically stable in the sense of Definition 6. b)The ellipsoid E(Q,ec,R∗)in (5)withR∗≤1 is an invariant set of attraction for the system (2)under switching rule (12)whene(k)∈E(Q,ec,1)and switching rule (18)whene(k)∉E(Q,ec,1).Thus,system (2)is globally practically asymptotically stable in the sense of Definition 6. c)Let the conditions of Proposition 3 be satisfied.Then,the ellipsoid E(Q,ec,R∗)in (5)withR∗>1 is an invariant set of attraction for the system (2)under switching rule (12).Thus,the system (2)is globally practically asymptotically stable in the sense of Definition 6. Proof:The proof follows from the fact that the conditions of Proposition 2 are embedded within the conditions of this theorem.As a result,the ellipsoid E(Q,ec,1)in (5)is an attractive set under switching rule (18)outside of it.Now items a)–c)are inferred from items a)–c)of Proposition 4. ■ Thanks to the conditions of Proposition 3 in item c)of Theorem 2,the switching rule in this item is considered identically as (12)in the whole state space.Another switching procedure is to use (12)within E(Q,ec,R∗)and (18)outside of it. Theorem 2 offers the same theoretical advantages of Theorem 1 plus the additional merit of matrix inequalities with smaller dimensions that may be more numerically tractable.This is because the matrix inequalities and the associated decision variables in (13)and (14)related to the invariance condition are eliminated in Theorem 2. It should be noted that Theorems 1 and 2 cover the following special design cases available in the literature and provide a unified version of the current results. 1)Centralized Lyapunov Function and CentralizedEllipsoid (CLCE):In this case,in (3),h=0n,d=0.In addition,ec=0nin (5)orc=0n,ρ=−1 in (4).Moreover,one can takeP=QorP≠Qin (3),(4),or (5).The stabilization techniques in [11],[16],[17],[22] fall into this category. 2)Decentralized Lyapunov Function and Centralized Ellipsoid (DLCE):In this case,the vectorhand scalardin (3)are not set to zero necessarily.However,as in the case of the CLCE scenario,ec=0nin (5)orc=0n,ρ=−1 in (4).In [9],the authors used these types of Lyapunov functions and ellipsoids in their study. 3)Centralized Lyapunov Function and Decentralized Ellipsoid (CLDE):This case considers the Lyapunov function in (3)with pre-assigned parametersh=0n,d=0.However,in contrast to CLCE and DLCE cases,the vectorsecandcare not removed in (5)and (4),respectively.Moreover,scalar ρ is not preset to–1 in (4).The work in [23] and [10] falls into this category. In what follows,the proposed method in this paper using a decentralized Lyapunov function and decentralized ellipsoid is abbreviated as DLDE.It is noted that the approach in [24] is a particular case of the DLDE method in which the invariant set is considered dependently as the level sets of a shifted quadratic Lyapunov function.While in the general decentralized setting of the DLDE method,the shifted Lyapunov function and the shifted invariant ellipsoid are parameterized independently. To achieve better performance with minimum deviations from the setpoint,we are interested in selecting the invariant set of attraction with a small size as far as possible.In this regard,one technique is to minimize the ellipsoid volume through the minimization ofdet(Q−1)[7],[9],[31].In [28],it is shown that where ρi(Q−1)is the length of each semiaxis of the ellipsoid E(Q,ec,1)in (5).The product∝Vol(E(Q,ec,1))that is proportional to the ellipsoid volume may admit a substantial value of one semiaxis,while all others may be very small.As a result,the minimum volume criterion through the minimization ofdet(Q−1)may not give good performance in all directions.Another approach is to use the trace of the matrixQ−1that defines the sum of the squares of the ellipsoid E(Q,ec,1)semiaxes [28].Since the tool YALMIP/MATLAB[32] was not able to handle the objective functiontr(Q−1),in what follows,we have modified it such that the software limitation is relaxed while the main property of the size minimization is preserved.Since we have the minimization of λmax(Q−1),guarantees the minimization√of the corresponding maximal semiaxisρmax(Q−1)=.Moreover,it minimizes an upper-bound fortr(Q−1).Therefore,the ellipsoid size minimization problem is formulated as On the other hand,by introducing a slack variablet>0,we have [33] Using (38)and Schur complements,the optimization problem in (37)can be equivalently rewritten as As it will be shown in the next section,the trajectories of the system converge to the center of ellipsoids (4)and (5)atec=−Q−1cwhich in general does not coincide with the desired equilibrium pointxe.To solve this problem,we add a new term of ∥ec∥2=to the optimization problem’s cost function (39)to achieve the following multiobjective nonlinear programming in whichwis a weighting factor determined by the designer. The optimization problems in (37)–(40)are formulated for Theorem 2.They can be easily modified to handle the conditions of Theorem 1 by embedding the additional constraints (13)and (14)and decision variables λ1i,i∈K,τ1≥0.In this paper,the optimization problems in (39)and(40)are solved via solver PENBMI [34] interfaced by YALMIP [32].The PENBMI solver is suitable for optimization problems with a quadratic objective function and BMI constraints.It provides a local solution when convergence is achieved [34]. In this section,various examples are introduced to illustrate the previous results.It should be noted that,in contrast to the pure LMI based optimization problems [35],making a fair comparison among BMI based optimization problems and formulations is a difficult task.The reason is that the BMI based optimization problems are non-convex,and exploring for a global optimum is an NP-hard problem.In most cases,the convergence of the various iterative techniques to find a local optimum is not guaranteed mathematically,and the choice of the initial value is important for convergence to an acceptable solution [36].Nevertheless,one can always compare various BMI formulations or BMI solution methods on various examples to take some statistical information about various methods [37]. Example 1:This example is borrowed from [10].Here,to obtain acceptable solutions from PENBMI software,we chooseTs=0.05.We consider the discrete-time switched affine system consisting of 2 unstable systems defined by the following state-space matrices: The state-space matricesAiandli,i∈{1,2},corresponding to the discrete-time system,can be obtained as Two different types of equilibrium points are taken for the numerical experiments.First,we adopt an equilibrium pointxe=[−1.3415 0.5864]Tcorresponding to λ=[0.4 0.6]Twhich belongs toXe={xe∈Rn|xe=(In−Aλ)−1bλ,λ ∈Λ}.Xeis the set of equilibrium points of the averaged system,which is indeed a convex combination of all subsystems of (1)asx(k+1)=∑i∈Kλi(Aix(k)+bi),λi∈Λ.Next,we consider the desired equilibrium pointxe=[−1 0]T,which is not the equilibrium point of the averaged system and does not belong to the setXe.The numerical results are given in Table I.Inthis table,the symbol– denotes that the optimization problem(40)has not been implemented for the case studies of CLCE and DLCE where a centralized ellipsoid has been used,and,as a result,the center of the ellipsoid is aligned with the chosen equilibrium point.In some cases,the PENBMI software did not provide acceptable solutions with the less conservative positiveness condition in (21).In these cases,this condition is replaced by the conventional and conservative one,namely,P≻0 in the case of the centralized Lyapunov function or[P h;hT d]≻0for the decentralized Lyapunov function.The superscript ∗ in Tables I and II reflects such situations.Moreover,in this example,the weighting factorwin the optimization problem (40)is set tow=9 except in one case for which the optimization problem (40)did not yield a feasible solution,andw=8 was selected.According to Table I,the advantages of the proposed DLDE method are highlighted when the equilibrium point is selected out of those that are attainable in the setXe.In this regard,the state trajectories corresponding to the equilibrium pointxe=[−1 0]T∉Xeand respective ellipsoids are shown in Fig.1.The corresponding switching sequence σ(k)is shown in Fig.2.In this study,Theorem 1 did not provide any feasible solution for the DLCE method and Theorem 3 is used instead.As can be seen from this figure,with approximately identical steady-state error in all case studies,the proposed DLDE method represents the smallest invariant set of attraction compared to other methods.More specifically,the invariant set’s size is 54.03% smaller than that of the best result of other scenarios,i.e.,the CLDE method.Fig.3 shows the state trajectories and corresponding ellipsoids when the multiobjective optimization problem (40)is employed in the CLDE and DLDE methods.As can be seen from this figure,in this case study,the DLDE method's performance is very close to the CLDE and DLCE methods.The time evolutions of the error state vectore(kTs)are illustrated in Fig.4 where the state trajectoryx(kTs)starts fromx0=[1 1]T.It is clear that after the transient the state remains near the equilibrium point whenxe∈Xe.However,there exists a steady state error whenxe∉Xe. TABLE I ELLIpSOID SIzE COMpARISONS FOR NUMERICAL EXAMpLE 1 TABLE II ELLIpSOID SIzE COMpARISONS FOR NUMERICAL EXAMpLE 2 Fig.1.State trajectories of example 1 corresponding to conditions of Theorem 1 for CLCE,CLDE and DLDE and Theorem 2 for DLCE using optimization (39)when xe=[−1 0]T ∉Xe. Fig.2.Switching function profile corresponding to Fig.1,(a)CLCE;(b)DLCE;(c)CLDE;and (d)DLDE. Example 2:Fig.5 shows the circuit diagram of a DC-DC buck converter.The continuous states of the system are defined asx(t)=[iL(t),vo(t)]T,which are the inductor current and converter output voltage,respectively.The state-space equations of this converter are as follows [38]: where Fig.3.State trajectories of Example 1 corresponding to conditions of Theorem 1 for CLCE,CLDE and DLDE and Theorem 2 for DLCE using optimization (40)for CLDE and DLDE methods when xe=[−1 0]T ∉Xe. Fig.4.Time evolutions of trajectories e(kTs)=[e1(kTs)e2(kTs)]T in Example 1 by the DLDE method,Theorem 1 and optimization (40).(a)Time evolution of e1(kTs);(b)Time evolution of e2(kTs). Fig.5.DC-DC buck Converter. The discrete-time system matricesAiandli,i∈{1,2},can be obtained by (41).The parameters used for the numerical experiments are given in Table III.To avoid ill-conditioned matrix inequalities and to make the problem more amenable for numerical purposes,we use per unit parameters in the numerical experiments [22],[26],[38].The per-unit value of a parameter is calculated by dividing its real value into thecorresponding base value.The base parameters are selected asvbase=50 V,ibase=andTbase=10 μs.The sampling time is set toTs=10 μs,and,as a result,the maximum value of switching frequency is limited to 1/2Ts=50 kHz=fs.Similar to Example 1,two different equilibrium points are chosen in this example.One is selected as the equilibrium point of the averaged system asxe=(In−Aλ)−1bλ=[0.0354,0.3960]Tp.u.∈Xecorresponding to λ=[0.4 0.6]T.The other is chosen arbitrary asxe=[0 0.15]T∉Xe.The numerical results are given in Table II.As can be seen from this table,the advantages of the proposed DLDE method are highlighted when the equilibrium pointxeis outside of the setXe.Figs.6 and 7 show the state trajectories and the corresponding switching sequences for the equilibrium pointxe=[0 0.15]T∉Xeusing conditions of Theorem 1 and optimization problem in (39).In this case study,the conditions of Theorem 1 did not provide an acceptable solution for the CLDE method,and therefore,the conditions of Theorem 2 are used.As can be seen from Fig.6,compared to other scenarios,the proposed DLDE method yields the best solution in terms of the smallest invariant set of attraction and closeness of the state trajectories to the selected equilibrium point.The resulting ellipsoid is 75.66% smaller than that of the best result of the other methods in CLCE and DLCE.In the CLDE method,after a certain time,the switching function is fixed on σ(k)=2,and the state trajectories converge to zero eventually,which is not acceptable in practice for switching converters.This issue highlights the significance of multiobjective optimization in(40).In this regard,Fig.8 illustrates the state trajectories and the corresponding ellipsoids when the optimization (40)is employed for the CLDE and DLDE methods.The switching signal profiles corresponding to the CLDE and DLDE methods in Fig.8 are shown in Fig.9.As can be seen from these figures,utilizing multiobjective optimization (40),the problem associated with the CLDE method discussed in Figs.6 and 7(c)is fixed.Moreover,in contrast to the similar case study in Example 1 (Fig.3),the smallest steady-state error and invariant set size are obtained for the proposed DLDE method.The invariant set size is 58.05% smaller than that of the best result of the other scenarios,i.e.,the CLCE method.Fig.10 shows the time evolutions of the error state vectore(k)when the state trajectoryx(k) starts fromx0=[1 1]T.Similar to Fig.4,there exists a steady state error whenxe∉Xe,while it disappears whenxe∈Xe.The preceding examples illustrate the effectiveness and validity of the proposed DLDE stabilization method.It should be noted that the numerical results presented in this paper are extracted via the PENBMI/YALMIP tool that is a local optimizer.As a result,a degree of conservativeness is inherent in the presented results.Although the BMI formulation is by itself reliable,flexible,and less-conservative,however,the optimization problems associated with the BMI problems are non-convex and achieving a global optimal solution is an NP-hard problem.In this respect,developing suitable global optimization tools to achieve better numerical results from the BMI problems will play a key role in this field of research. TABLE III THE SpECIFICATIONS OF THE DC-DC BUCk CONvERTER Fig.6.State trajectories of Example 2 corresponding to conditions of Theorem 1 for CLCE,DLCE and DLDE and Theorem 2 for CLDE using optimization (39)when xe=[0 0.15]T ∉Xe. Fig.7.Switching function profile corresponding to Fig.6,(a)CLCE;(b)DLCE;(c)CLDE;and (d)DLDE. Fig.8.State trajectories of Example 2 corresponding to conditions of Theorem 1 for CLCE,DLCE and DLDE and Theorem 2 for CLDE using optimization (40)in CLDE and DLDE when xe=[0 0.15]T ∉Xe. Fig.9.Switching function profile corresponding to Fig.8 for CLDE and DLDE methods,(a)CLDE;(b)CLDE enlarged view;(c)DLDE. In this paper,the global practical stabilization of the discrete-time switched affine systems via state-dependent switching rules has been investigated.The main contribution relies on extending the existing results by the simultaneous use of a decentralized quadratic Lyapunov function and a decentralized ellipsoid.Two different stability conditions are provided:a purely numerical method and a numericalanalytical one.A multiobjective optimization problem was formulated such that its solution makes it possible to minimize the size of the ultimate invariant set of attraction and the steady-state errors of the system trajectories.The proposed stabilization method was compared with other existing methods in which it is necessary for the Lyapunov function or the employed ellipsoid or both be of the centralized type.The numerical illustrations on an academic example and a DC-DC buck converter show that the proposed stabilization strategy provides less conservative results and yields a smaller invariant set of attraction and less steady-state errors of the system trajectories. Fig.10.Time evolutions of trajectories e(k)=[e1(k)e2(k)]T in the Example 2 by the DLDE method,Theorem 1 and optimization (40).(a)Time evolution of e1(k);(b)Time evolution of e2(k). APPENDIX Proof of Proposition 1:It is shown that (13)and (14)imply condition a)of Lemma 1.Pre-multiplying (13)by [e(k)T1]and post-multiplying it by [e(k)T1]Tone can reach ∀e(k)∈Rn.Inequality (42)can be rewritten as Using S-procedure [31],(43)implies By substitutingM1,M2and,M3from (15)–(17)into (44)and using (4),one can write According to (14),since ∑i∈Kλ1i>0,λ1i≥0,i∈K,from(45),one can conclude Based on the switching rule in (12),one can write According to (2),e(k+1)=Aσ(e(k))e(k)+lσ(e(k)),thus from(46)and (47),one can conclude which states that whenevere(k)∈E(Q,c,ρ) thene(k+1)∈E(Q,c,ρ).Thus,according to condition (a)of Lemma 1,(48)implies that the ellipsoid E(Q,c,ρ)is aninvariantset for the switched affine system (2)under switching rule (12). ■ Proof of Proposition 2:It is shown that conditions (19)and(20)imply item b)of Lemma 1,and condition (21)satisfies item c)of this lemma.From (19),one can conclude ∃γ>0 such that This comes from the fact that for a symmetric matrixM=MT∈R(n+1)×(n+1),we have.Pre-multiplying (49)by [e(k)T1] and post-multiplying it by[e(k)T1]Tone can obtain The second inequality in (50)comes from the fact that−γe(k)Te(k)≤0.(50)can be rewritten as Using the S-procedure,(51)implies According to (20)and (3),from (53)one can conclude Based on the switching rule (18),we have From (54)and (55)one can reach which implies condition (b)in Lemma 1.According to item c)of Lemma 1 we still need to show that the functionv(e)in (3)is positive definite whene(k)∉E(Q,c,ρ).Pre-multiplying (21)by [e(k)T1] and post-multiplying it by [e(k)T1]T,one can obtain Using the S-procedure,and according to (3)and (4),(56)implies e(k)∉E(Q,c,ρ)⇒v(e(k))>0 which verifies the condition c)of Lemma 1.As a result,conditions b)and c)are satisfied,and the attractiveness of the ellipsoid E(Q,c,ρ)under switching rule (18)is concluded. ■ Proof of Lemma 2:We consider the scalar functionv(e(k))as which is positive definite ∀e(k)∉E(Q,c,ρ).Thus,condition c)of Lemma 1 is satisfied.In the sequel,it is shown that the condition b)of Lemma 1 is implied by (25).Using (57),we construct the following switching law and show that it makes the ellipsoid E(Q,c,ρ)in (4)an attractive set for the system(2): Now,according to (58),one can write Using (25)and (59),one can reach Now,we define function ϕi(e(k))as According to (60)and (61),|S|≥1 and ϕi(e(k))>0 whene(k)∉E(Q,c,ρ).Now,we define the function ϕ(s)as Function ϕ(∥e(k∥)is nondecreasing and positive definite whene(k)∉E(Q,c,ρ).Moreover,according to (61)and (62),one can write Sincee(k)∉E(Q,c,ρ),using (4),we have BecauseQ=QT≻0,one can writee(k)T Qe(k)≤λmax(Q)∥e(k)∥2.Moreover,cTe(k)≤∥c∥∥e(k)∥.By substituting these inequalities into (64),one can obtain According to (65),one can conclude that Using (66)and the nondecreasing nature of function ϕ(s)in(62),one can get which together with (63)yields ∆v(e(k))≤−ϕi(e(k))≤−ϕ(∥e(k)∥)≤−γ<0,i∈S. Therefore,conditions b)and c)in Lemma 1 are fulfilled,and the attractive property of the ellipsoid E(Q,c,ρ)is concluded. ■ Proof of Proposition 4:i)Let us assume thate(k)∈E(Q,ec,1).Then,according to (5),(e(k)−ec)T Q(e(k)−ec)≤1 and since λmin(Q)∥e(k)−ec∥2≤(e(k)−ec)T Q(e(k)−ec),then, Since,|∥e(k)∥−∥ec∥|≤∥e(k)−ec∥,from (67),one can conclude Using (2),one can write According to (68)and (69),one can conclude Now,using(e(k+1)−ec)T Q(e(k+1)−ec)≤λmax(Q)×∥e(k+1)−ec∥2and (70),one can write The term at the right-hand side of (71)is identical to the parameterRin (35).IfR≤1,from (71)one can conclude that(e(k+1)−ec)T Q(e(k+1)−ec)≤1.Thus,whenevere(k)∈E(Q,ec,1)thene(k+1)∈E(Q,ec,1)as well.This means that ellipsoid E(Q,ec,1)is an invariant set independent of any switching strategy within E(Q,ec,1).This result together with the attractiveness property of E(Q,ec,1)implies that the ellipsoid E(Q,ec,1)is an invariant set of attraction independent of any switching rule inside of it. ii)Let us assumee(k)∈E(Q,ec,1).Under switching rule(12)that according to Lemma 3 is equivalent to the switching law in (26),one can write The last inequality in (72)comes from our arguments in the proof of the item i)where the constraint (e(k)−ec)T Q(e(k)−ec)≤1implies (67).The term at the right-hand side of the last inequality in (72)is equal to the parameterR∗in (36).IfR∗≤1,one can conclude that,under switching rule (12),e(k)∈E(Q,ec,1)impliese(k+1)∈E(Q,ec,1).This means that E(Q,ec,1)is an invariant set via the switching rule (12)within it.This result,together with the attractiveness property of E(Q,ec,1),implies that the ellipsoid E(Q,ec,1)is an invariant set of attraction when the switching rule (12)is implemented inside of it. iii)IfR∗>1,then E(Q,ec,1)⊂E(Q,ec,R∗).The rest of the proof is provided in two parts: Case 1(e(k)∈E(Q,ec,1)):In this case,following our arguments in the proof of the item ii),the implementation of the switching rule (12)or its equivalent (26),within E(Q,ec,1)implies whenevere(k)∈E(Q,ec,1),then according to (72),(e(k+1)−ec)T Q(e(k+1)−ec)≤R∗or analogouslye(k+1)∈E(Q,ec,R∗). Case 2(e(k)∈E(Q,ec,R∗)−E(Q,ec,1)):In this case,since conditions of Proposition 3 are valid,so are the equivalent conditions of Lemmas 2 and 4 (please see the proof of Proposition 3).According to Lemma 4,one can conclude∃i∈Ksuch that ∀e(k)∉E(Q,ec,1).Using (73),the implementation of the switching rule (12)or its equivalent (26)within E(Q,ec,R∗)yields According to (74),one can conclude(e(k+1)−ec)T Q(e(k+1)−ec)<(e(k)−ec)T Q(e(k)−ec).Sincee(k)∈E(Q,ec,R∗),thus (e(k)−ec)T Q(e(k)−ec)≤R∗that together with(e(k+1)−ec)T Q(e(k+1)−ec)<(e(k)−ec)T Q(e(k)−ec)yields(e(k+1)−ec)T Q(e(k+1)−ec)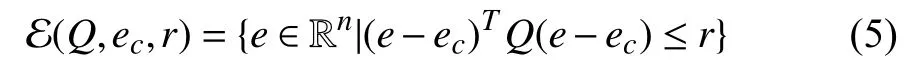




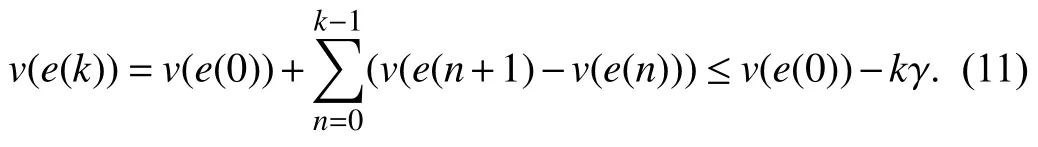
III.STABILITY ANALYSIS AND CONTROLLER SYNTHESIS
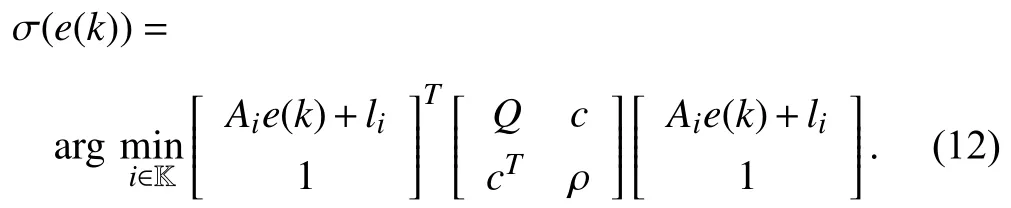
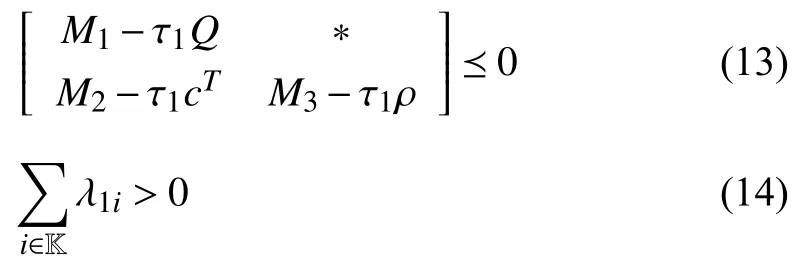
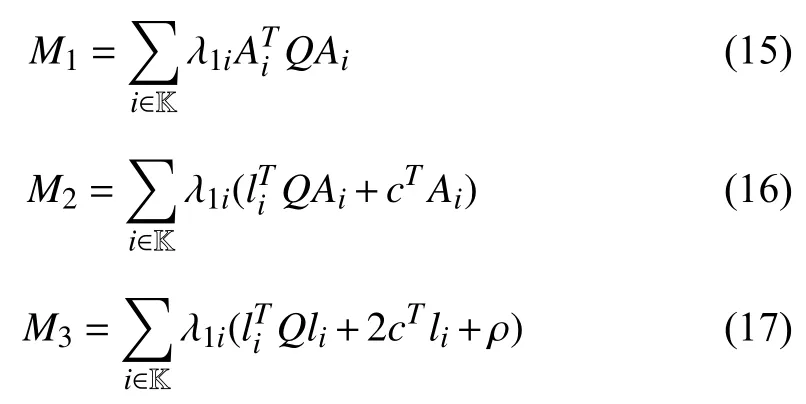
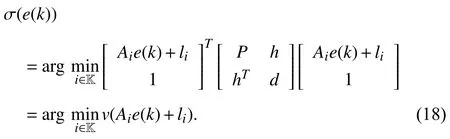


IV.NUMERICAL-ANALYTICAL METHOD AND POSSIBILITY OF THE UNIFIED SwITCHING IN THE WHOLE STATE SpACE
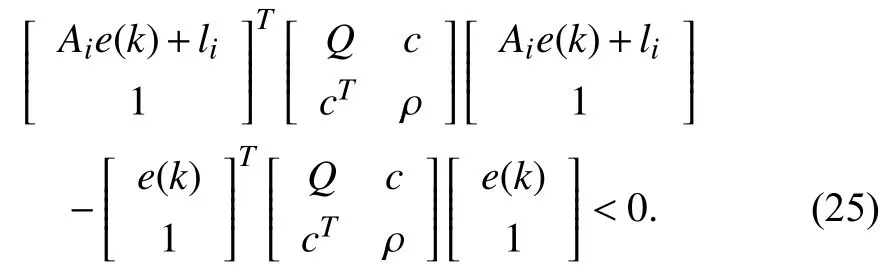
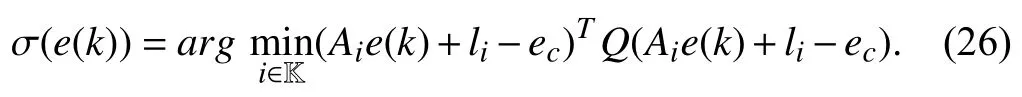

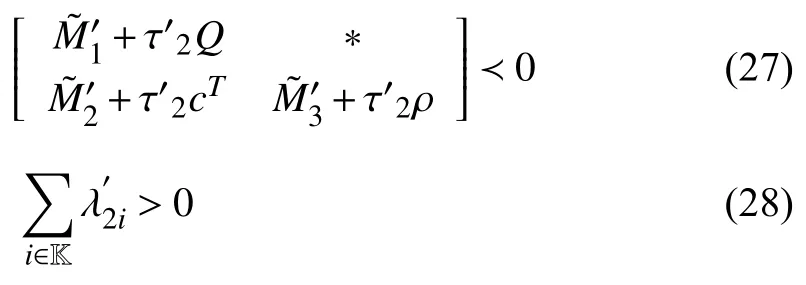



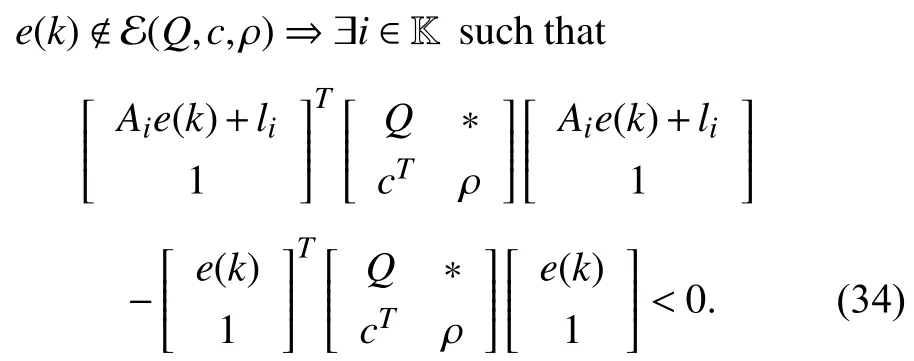
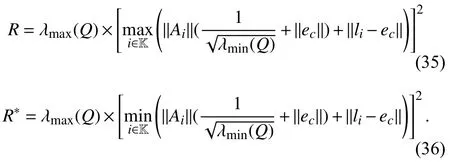
V.MINIMIzATION OF THE INvARIANT SET OF ATTRACTION AND NUMERICAL ASpECTS

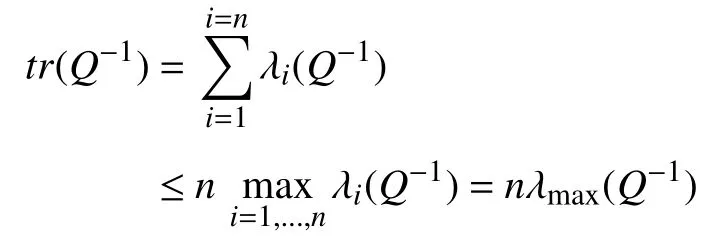
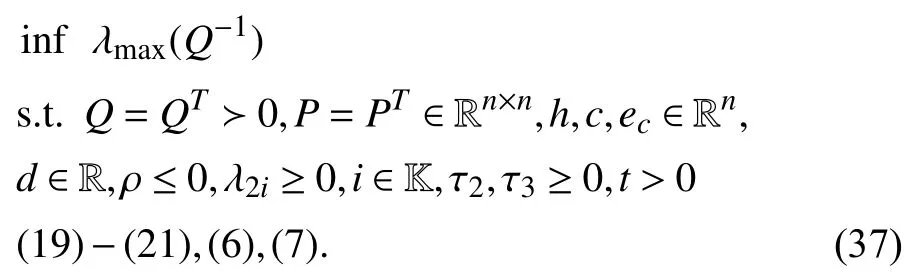

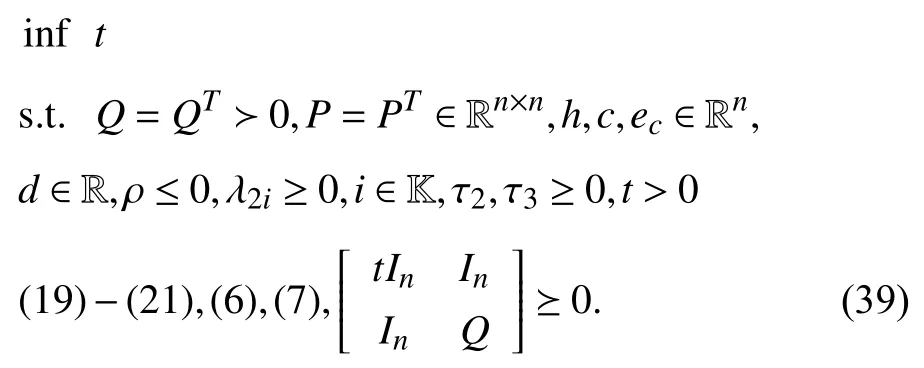
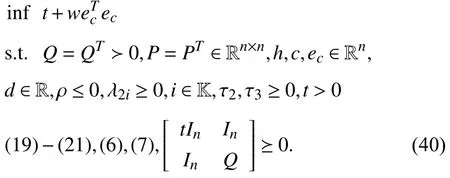
VI.EXAMpLES





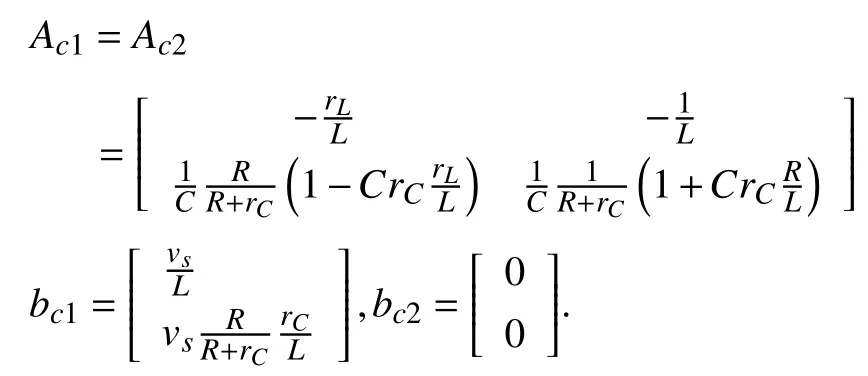




VII.CONCLUSION

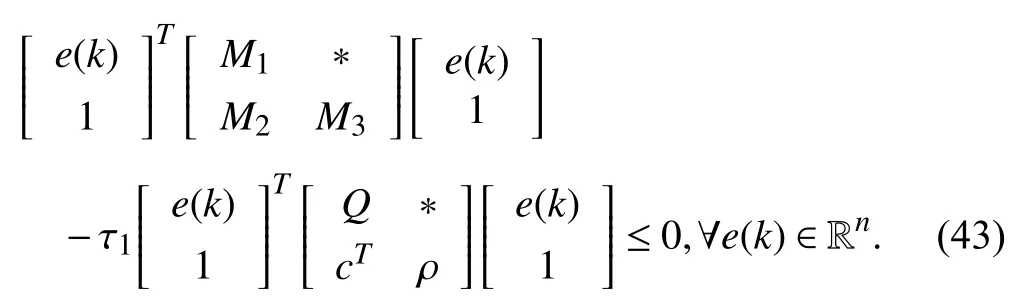
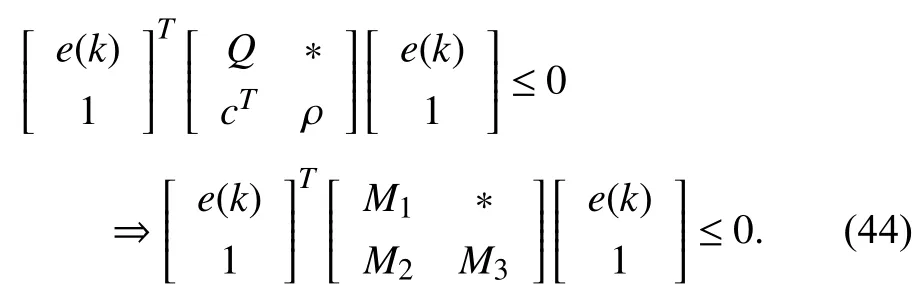

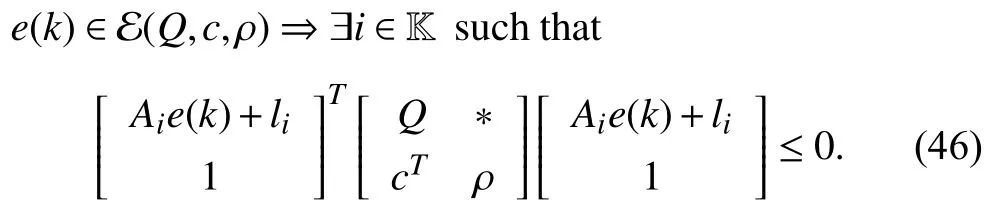

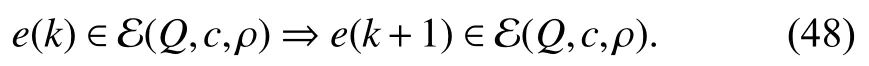
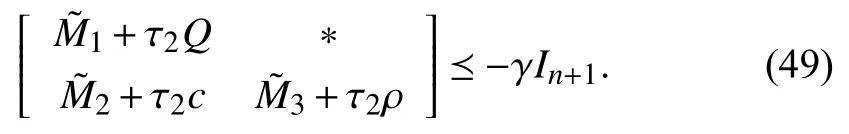
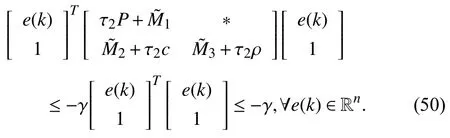

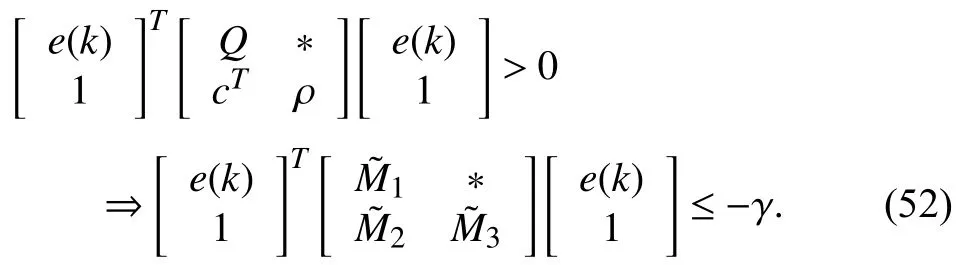
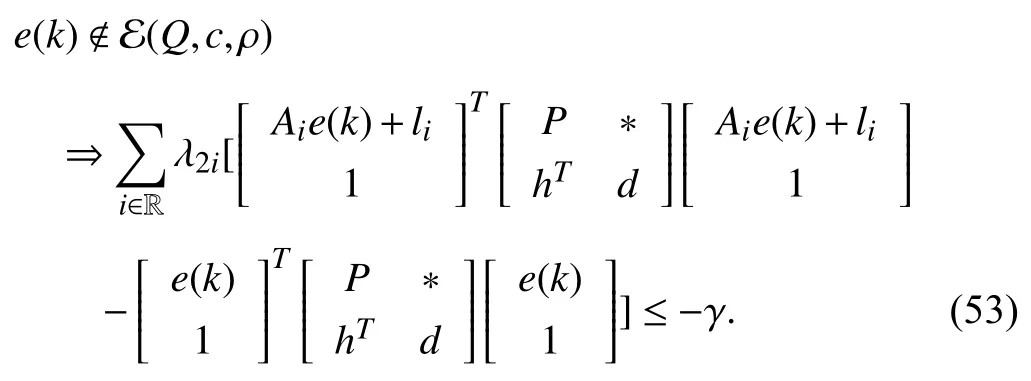


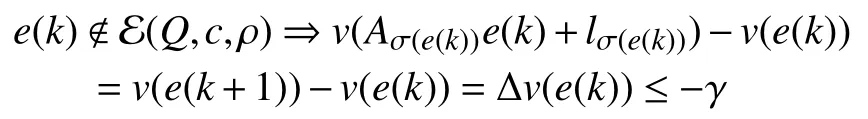

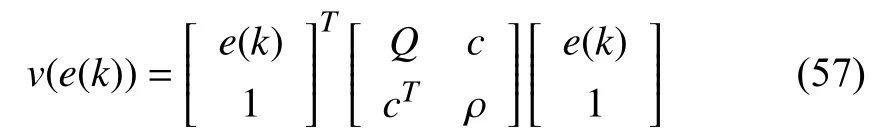
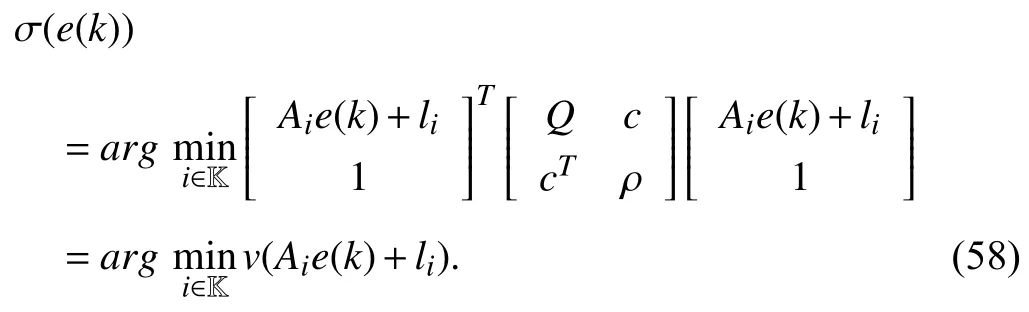
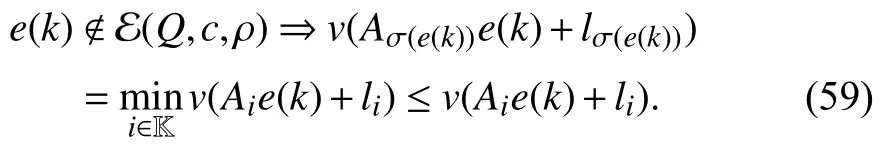
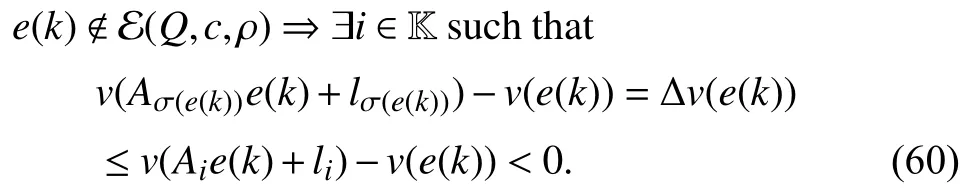
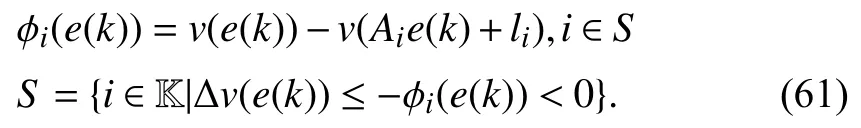
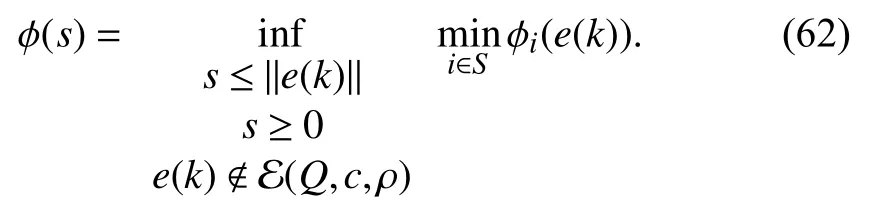
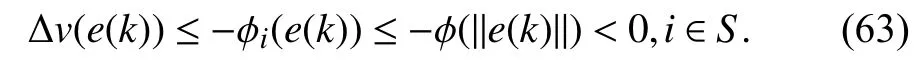

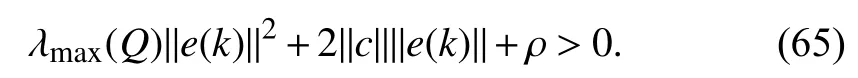
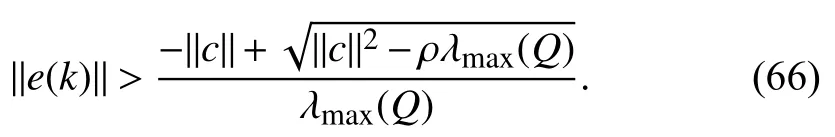

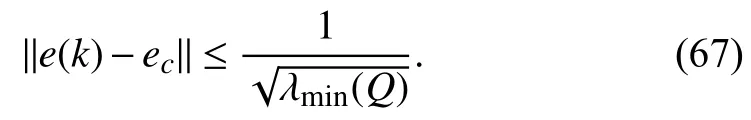




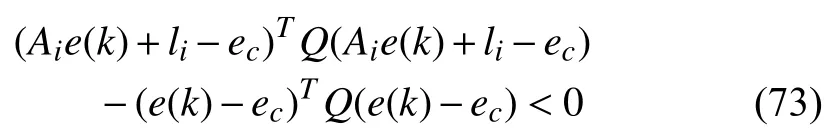

 IEEE/CAA Journal of Automatica Sinica2021年11期
IEEE/CAA Journal of Automatica Sinica2021年11期
