条形基础下砂-黏土双层地基极限承载力预测模型的不确定性分析

关 宇, 张毅博

(中国人民大学 a.审计处；b.国际交流处,北京 100872)

地基承载力是土力学中的一个经典问题。均匀土层上条形浅基础在竖向荷载作用下的极限承载力一般采用太沙基承载力公式来确定。在实际工程中，成层土是常见的现象，由各种自然因素或人为因素造成[1]。在地基处理中，一般采用砂土来替换上层的软粘土层以提高地基承载力。这就形成了上砂下黏的双层地基，这种双层地基的破坏模式比均匀土层更为复杂，其破坏面可能仅在砂土层范围内，也可能延伸到下卧黏土层。目前对于这种砂-黏土双层地基的极限承载力问题已有较多的研究，其研究方法主要有极限平衡法[2-4]、极限分析法[5-8]、实验方法[3，9-14]和数值分析法[1，15-17]等。其中，在极限平衡法的基础上，逐渐演化和发展出了不考虑剪切强度，将土层重度超载化的应力扩散法[4]和假设土层完全剪切且被动失效的冲剪破坏法[2-3]。这2种方法都是基于理想假设条件下的半理论半经验方法，参数简单、易于理解，对于解决地基极限承载力的工程问题发挥了重要的作用。但是基于理想假定条件下产生的系统误差往往会使理论结果与工程实际产生较大的偏差。

岩土工程的可靠性理论是在统计学方法和概率论方法的基础上不断发展和完善的，由于解决岩土工程问题的数学模型、数值分析程序等都是基于一定理想化条件的，理论基础往往不能够完全反映工程实际，计算结果也不够准确，因此不确定性成为最大的特点。这种基于理想条件下的不确定性被认为是认知不确定性[18]。在对岩土工程实际问题的可靠性设计过程中，如何分析理想模型的认知不确定性成为重中之重[19]。对于条形基础下，砂-黏土双层地基极限承载力的预测问题，Tang等[20]收集了一个包括离心机试验得到的承载力数据库，并结合有限元方法对这2种工程中最常用的半经验方法进行了不确定性分析和经验性修正。研究结果没有提出新的计算方法，仍然是在此2种方法假设的破坏模式基础上得到。

文中针对竖向荷载时条形基础下的砂-黏土双层地基极限承载力问题，提出一种不依赖于破坏模式假设的计算方法，并对该设计方法进行不确定性分析。采用极限分析上限法对承载力进行数值计算，得到不同工况下的设计图表，并对参数进行敏感性分析。基于计算结果提出了预测极限承载力的简化公式。收集了基于不同方法研究中得到的砂-黏土双层地基极限承载力预测值，建立数据库，基于此数据库对文中的数值结果和得到的简化公式进行统计学不确定性分析。

1 数值模型及验证

1.1 数值模型

图1是数值模型示意图。在砂-黏土双层地基上放置了一个刚性条形基础。B是基础宽度。砂土没有黏聚力，φ是摩擦角，D是厚度，γ是重度。黏土没有摩擦力，c是黏聚力。砂土层假设排水、黏土层假设不排水。基础与砂土层的交界面认为完全粗糙，这一摩擦角与砂土摩擦角相等。

图1 数值模型

文中使用计算软件LimitState:GEO[3]基于不连续布局优化(discontinuity layout optimization,DLO)算法来计算地基承载力。DLO是一种计算程序，基础是塑性理论，原理是极限分析上限法，在已有研究中被广泛应用于各种承载力计算[21-25]。根据不同的工况在建模时协调均匀地布置了网格密度，节点数量为3 000～5 000，在塑性区集中的局部区域进行了网格加密，这样做可以提高计算精度并保证计算结果协调一致。

1.2 数据库建立及模型验证

为了分析DLO方法计算得到的极限承载力准确性，作为进行不确定性分析的基础，收集了现有文献中砂-黏土双层地基的极限承载力数据，形成一个共包含81个数据[1，2，7，12，17，26-29]的数据库。为了便于分析验证，对数据库中的参数作无量纲处理，包括tanφ、c/γB、D/B以及qu,m/γB。基于此数据库，对每一个工况分别使用DLO方法对承载力进行计算，同样对其进行无量纲化，为qu,DLO/γB，与现有文献中的承载力进行比较，如图2所示。由图可见，这些对比数据的平均趋势非常接近1∶1线，几乎所有数据的误差都在20%之内。对比数据的决定系数R2(0.92)同样可以说明其准确性。上述特征表明，采用DLO计算的承载力与现有文献中的承载力近似度很高，证明了DLO方法在预测砂-黏土双层地基的极限承载力时比较精确。

图2 DLO计算结果(qu,DLO/γB)与文献结果(qu,m/γB)比较

在岩土工程领域，计算模型不确定性的评估通常以模型因子[19-20，30]为媒介，模型因子往往是通过实际测量值与该模型预测值的比来表征的。因此，为了表征DLO计算结果的不确定性，定义其模型因子λ为

λ=qu,m/qu,DLO

(1)

通过2个环节[20]对模型因子λ进行不确定性分析：1)对模型因子关于输入参数的依赖性进行分析；2)建立一个有意义的统计模型用来表征模型因子。基于Spearman相关系数[31]对模型因子λ分别关于输入变量(tanφ、c/γB和D/B)的依赖性进行分析。其中，Spearman相关系数是一种在统计学中常用的非参数指标，作用是对变量之间的依赖性进行量度，表示为τ，其值为+1时表示2个变量完全单调正相关，其值为-1时表示负相关。分别对不同模型因子的Spearman相关系数进行计算分析，如表1所示。其中，λ的关于所有输入变量的p值均大于0.05，从统计学考虑λ可以被看作一个随机变量。

表1 文中得到的Spearman相关系数

建立统计学模型用以表征λ。通过计算，λ的均值为1.01、标准差为0.15和变异系数为0.14。均值约等于1说明DLO方法的预测合理性，标准差、变异系数比较小，说明DLO方法的预测精确性。图3是λ的概率密度函数(PDF)和累计分布函数(CDF)，说明λ的分布在统计学上可以被看作符合对数正态。K-S检验[31]的p值远大于0.05同样可以说明这一点。

图3 λ的CDF和PDF

λ与各个参数分别独立，在统计学上被认为是一个随机变量，并且符合对数正态分布。结果表明，在统计学意义上DLO计算地基极限承载力时只有随机误差而不具有系统误差，其计算结果可以作为可靠度设计的依据。

2 承载力设计图表

采用DLO方法计算条形基础下砂-黏土双层地基极限承载力，参数取值如表2所示，在承载力变化的临界值附近加大计算工况的分布密度。在经典承载力理论的基础上，提出了承载力折减系数R：

表2 承载力参数取值

(2)

式中，qu,s为条形基础下纯砂土的地基极限承载力。根据太沙基承载力理论，qu,s计算公式为

(3)

图4为条形基础下，砂-黏土双层地基承载力折减系数R使用DLO的计算结果。与预想结果一致，R值与D/B呈正相关趋势，这是因为更厚的上层砂土对承载力起到更大的作用。当φ<42°时，不论c/γB取何值，当D/B增加到一定程度，R值最终都会逐渐趋于1，此时的砂-黏土双层地基承载力完全是由纯砂土进行承载的，下部黏土层对承载力的贡献为0，总体的破坏模式为Prandtl形式，并且破坏范围只在砂土层中。当φ≥46°时，R值在当前厚度范围内始终小于1，即砂-黏土双层地基承载力始终小于纯砂土承载力，此时的破坏面始终很大，黏土层仍然对承载力有所贡献。对于φ<42°的工况，存在一种由黏土层贡献承载力向黏土层不参与承载力的临界状态，此时的厚度称之为临界厚度(D/B)cri。可见，(D/B)cri与φ呈正相关关系，与c/γB呈现负相关。

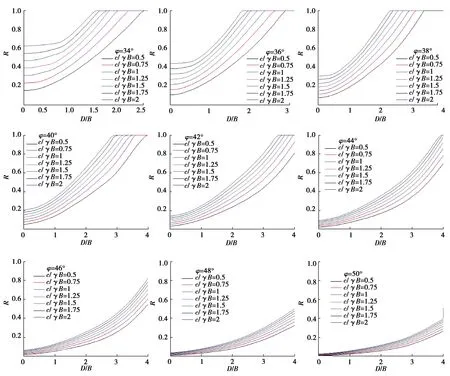
图4 地基承载力折减系数R设计图表

3 简化公式及不确定性分析

3.1 简化公式

预测模型采用多元回归(PR)的方法进行构建[20，32]。由图4可知，R值关于D/B的函数形如一个凹函数，其开口向上，这种形式与幂函数一致。定义这一函数的纵轴截距为R0，此时砂土层厚度为0，代表该工况下纯黏土承载力和纯砂土承载力的比值。基于以上计算数据，可以得到R值的多元回归模型为

R=(α1X0.2Y+α2X0.3+α3X+α4Y+α5)Z(-Xα6Yα7+α8)+R0，

(4)

表3 简化公式参数

3.2 不确定性分析

3.2.1η的不确定性分析

简化公式(4)得到承载力进行无量纲化为qu,c/γB，将其与DLO计算的承载力qu,DLO/γB进行对比，如图5所示。可以看到，对比数据的趋势与1∶1线非常接近，几乎所有点的误差都小于20%，决定系数R2为0.99。图5表明简化公式(4)可以较为精确地对DLO承载力的计算进行拟合。

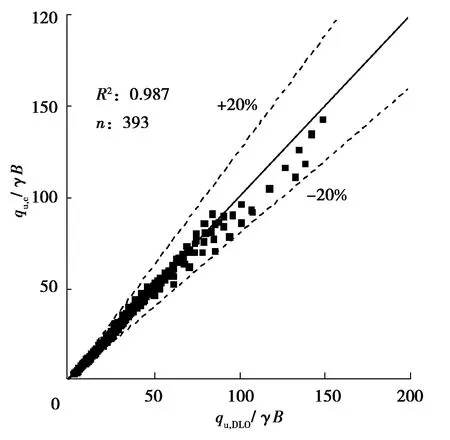
图5 简化公式计算结果(qu,c/γB)与DLO计算结果(qu,DLO/γB)比较

式(4)对于DLO计算结果的拟合存在不确定性，定义模型因子η为

η=qu, DLO/qu,c。

(5)

得出η的统计模型的先决条件是评估其对输入变量的依赖性。基于上述数据，分析所有的Spearman相关系数如表2所示。可见，3个输入变量均具有大于0.05的p值，η可以被看作一个随机变量。η的均值、标准差和变异系数分别为1.00、0.05和0.05。图6是η的累计分布函数(CDF)和概率密度函数(PDF)，通过K-S检验(p值为0.05)认为η符合对数正态分布。

图6 η的CDF和η的PDF

3.2.2 M的不确定性分析

将qu,c/γB与文献中的承载力qu,m/γB进行对比，如图7所示。可以看到，简化公式(4)预测结果接近现有文献的结果，平均趋势类似于1∶1线，决定系数R2为0.96。

图7 简化公式计算结果(qu,c/γB)与文献中计算结果(qu,m/γB)比较

定义模型因子M为

M=qu,m/qu,c。

(6)

通过文献中的81个数据，计算M与3个输入变量的Spearman相关系数如表2所示。3个输入变量的相关系数p值均比0.05大，说明M不具有系统误差，可以被看作随机变量。M的均值、标准差和变异系数既可以直接计算得到，也可以表示为2个随机变量(λ和η)的积：

M=λη。

(7)

因为λ和η均符合对数正态分布并且相互独立，所以M同样符合对数正态分布[33]，其均值和变异系数分别计算如下：

μM=μλμη，

(8)

(9)

式中，μM、μλ和μλ分别是M、λ和η的均值；δM、δλ和δη分别是M、λ和η的变异系数。

根据式(8)和式(9)可得，M的均值、标准差和变异系数分别为1.01、0.15和0.15。作为比较，由81个数据计算得到的M均值、标准差和变异系数分别为1.00、0.14和0.14，区别很小。

M、λ和η3个模型因子的均值都非常接近1；M和λ的变异系数较大且非常接近，但是η的变异系数要明显更小。根据式(9)，这一现象揭示了λ是M随机误差的主要来源，即简化公式关于DLO结果的预测模型具有很高的精度，而DLO方法关于文献承载力的预测较为粗略。图8是M的累计分布函数(CDF)和概率密度函数(PDF)，K-S检验p值为0.47，可知M可以被看作符合对数正态分布，这一结论与式(9)一致。

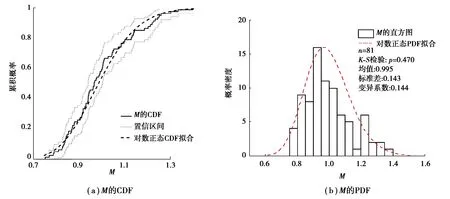
图8 M的CDF和PDF

4 结 论

使用极限分析上限法对条形基础下，砂-黏土双层地基极限承载力进行计算，绘制了设计图表用以表示承载力折减系数R。提出了简化公式用以预测极限承载力。收集了文献中的承载力计算结果，对DLO的计算和简化公式的计算不确定性进行分析，得到如下结论：

1)条形基础下，砂-黏土双层地基极限承载力的影响因素大体包括土体强度和几何尺度。承载力折减系数R与D/B呈正相关关系，这种情况下的破坏面超出了上层砂土的范围；当R等于1时，破坏面则不会延伸到软土层。根据这一转换定义了临界厚度(D/B)cri，这一临界厚度关于φ呈正相关，关于c/γB则相反。

2)条形基础下，砂-黏土双层地基极限承载力的DLO预测结果具备统计学意义上的可靠性。DLO关于文献承载力结果的预测模型因子λ可以被看作随机变量并且符合对数正态分布，其均值为1.01、标准差为0.14、变异系数为0.14。

3)提出的简化公式对承载力的预测具有计算精确、没有系统误差的特点。简化公式关于DLO计算结果和现有文献承载力结果的模型因子η、M可以看作随机变量并且符合对数正态分布，其中η的均值为1.00、标准差为0.05、和变异系数为0.05，M的均值为1.00、标准差为0.14、变异系数为0.14。M的随机误差主要来源于DLO对现有文献计算结果的预测。这一简化公式可以作为条形基础下，砂-黏土双层地基极限承载力可靠度设计的参考。