“四学课堂”理念下数学微专题研究课的教学设计——以初一“三角形中线与面积问题”为例

王盼盼 (江苏省张家港市第六中学 215638)

说起微专题研究，很多教师认为这应该是初三复习备考的事(如文[1])．其实不然，微专题研究是指围绕知识的重点、难点设计的，利用具有紧密相关的知识或方法形成的某些专题研究，或者是针对学生的知识盲点、疑点、易错点整合的，能够在短时间内解决的问题集，或者是围绕重点内容、关键能力适度进行的知识拓展、解题方法研究的数学活动．通过微专题的研究和教学，希望能帮助学生加深对所学知识的理解，强化前后知识的联系，形成清晰的数学知识网络，同时获得系统的数学研究方法，提高自身的数学素养，促进学生的深度学习．初一年级的数学教学，是初中三年基础知识学习、基本技能训练的阶段，教学内容相对而言较为简单．但是，初一学生的知识储备比较少，认知能力有限，对初中阶段的抽象性知识不容易理解与掌握,对解题方法也了解甚少，更难以熟练应用．因此，在初一年级的数学教学中，我们有必要设置一些教学时间短、针对性强、主题突出、具有一定的趣味性的微专题，来辅助我们的数学教学，帮助学生全面理解知识、掌握知识，适度拓宽知识面．本文以“三角形中线与面积问题”为例，谈谈初一数学微专题研究课的实践与思考，期望能对教学一线的教师有所帮助和启迪．

1 教学过程

1.1 引导先学，知识再现

在微专题研究课的学习中，预习是学习过程中的第一步，学生通过对以小题带知识、引方法的问题的研究，实现以下两个目标：一是夯实基础知识，熟悉基本方法，为后续学习作好铺垫；二是提升自主学习的能力，提高课堂教学的效率．这是“四学课堂”最基础的环节．

问题1 在△ABC中，AB=5，BC=8，BC边上的高AD=4．

(1)△ABC的面积为；

(2)在图1中作出△ABC的高CE，则CE的长为；

图1 图2

(3)如图2，若点F是BC边的中点，则△ABF的面积为；

(4)如图3，若点F是BC边的中点，G是BC边上一点，且BG∶GC=2∶1，则△AFG的面积为．

图3

设计意图通过问题驱动让学生回顾旧知，再现三角形的面积公式、三角形中线与面积的关系、等高三角形面积比等于对应底边长之比等相关知识，渗透利用等积法求三角形一边上的高的思想方法．通过学生的交流、展示，教师的点评，将学生零散的、碎片化的知识加以提炼，形成较为系统的、条理化的知识结构．

1.2 组织互学，知识巩固

在微专题研究课的学习中，教师既要着力培养学生的合作意识，根据学生的兴趣特点，设计一些小组互学的学习活动，让学生的思维在协同学习中走向深入，不断完善；更要通过设置高质量的、有探究性的数学问题，激发学生合作探究的积极性，让学生在不同的智慧融合中启迪心智，在不同的思维碰撞中迸发潜能，长足进步．这是“四学课堂”十分重要的环节．

问题2 已知△ABC的面积为16，BD是△ABC的中线．

(1)如图4，若点E是AB边的中点，连结DE，则S△ADE∶S△ABC=；

图4 图5

(2)如图5，若点F是BD的中点，连结AF，G是AF上一点，且AG∶GF=1∶2，连结CF，CG，则△CFG的面积为．

设计意图问题2围绕三角形中线分割图形展开．教学过程中，要先给学生充足的独立思考时间，再进行小组交流、全班展示．通过问题的解决，让学生弄清问题的本质，积累数学探究活动的经验．第(1)小题的设置，目的是希望学生认清线段DE是△ABD的中线，为以后学习三角形的中位线作好准备；设置第(2)小题，一是要求学生认清△AFC的特征，二是要求学生明白△AFC的面积与△ABC的面积之间的关系，通过求解△CFG的面积，进一步巩固等高三角形面积关系的相关知识．在教师点评环节可以作如下变式：如图6，在△ABC中，BD是△ABC的中线，点E是BD上一点，BE∶ED=1∶2，连结AE，点F是AE上一点，AF∶FE=1∶2，连结DF．若△DEF的面积为m，则△ABC的面积为．借此提高学生的识图能力，熟练应用相关知识解决综合性问题．

图6

1.3 提升研学，知识综合

在微专题研究课的学习中，除了要引导学生理解基础知识，掌握基本技能，感悟数学思想，积累数学基本活动经验外，更重要的任务是促进学生数学学科素养和关键能力的不断提升．因此，在前面简单研究的基础上，要及时对所学知识进行适度的拓宽、引申，提升思维的层级，引发学生的数学思考，不断激发学生的学习兴趣，提高学生分析问题和解决问题的能力．这是“四学课堂”最关键的环节．

问题3 如图7，AD，BE分别是△ABC的两条中线，AD，BE交于点O．

图7

(1)S△AOES△BOD；(填>，=或<)

(2)求△BOD与四边形ODCE的面积之比；

(3)利用上述结论，你还有什么发现？

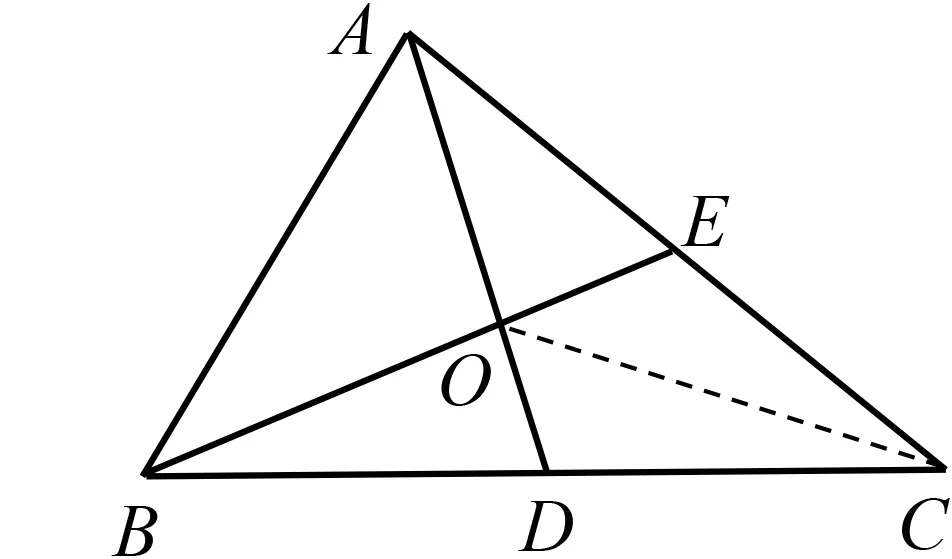
图8

1.4 迁移再学，知识深化

在微专题研究课的学习中，适时地将所学知识、解题方法进行有效的拓展、迁移，进而引领学生实施数学思维方式的有效迁移，才能让学生对数学问题的思考逐步走向深入，继而形成问题解决的思维方法，并将它内化为解决数学问题的技能与技巧，不断增强学生的数学悟性，生成智慧．这是“四学课堂”必须强化的环节．

图9

问题5 如图10，在锐角△ABC中，M是BC边上的一个动点，作射线AM，过点B，C分别作AM的垂线，垂足分别为点D，E．已知△ABC的面积为16，BC=8．

图10

(1)当AM=6时，求BD+CE的值；

(2)求BD+CE的最大值．

2 教学反思

2.1 简约而不简单的铺垫强化

初一学生刚开始接触微专题研究课，在设计微专题研究课教学内容、教学流程时，既要根据教学实际需要，合理规划、科学设置，更要兼顾初一学生的认知水平、知识储备、能力发展．在“引导先学，知识再现”环节，要通过简单的数学问题，帮助学生全面回顾已有知识、基本方法；在“组织互学，知识巩固”环节，要有针对性地设置一些与问题环节相匹配的问题，通过学生的小组合作学习、相互交流、全班展示，进一步巩固后续学习所需的知识、方法，切实提高学生的解题能力．这样简约而不简单的铺垫强化，教师要予以重视．

2.2 适度而不超越的拓展延伸

教材是重要知识点的精华与浓缩，往往言简意赅，或者限于篇幅，有些过程未能加以说明，特别是所选择的例题常常是围绕当堂内容展开的．教师作为教材与学生之间的协调者，有必要对教学内容进行适度的拓展延伸，这样的补充内容可以通过微专题研究课来实现．在“提升研学，知识综合”环节，要及时对前面所研究内容进行拓宽加深，完善学生认知体系，使得教学内容变得丰盈、有层次、有内涵，增强学生学习数学的信心．在“迁移再学，知识深化”环节，一要加强前后知识的联系，通过设置高质量的、有思维含量的问题，提高学生的高阶思维能力，完善学生的思维品质；二要兼顾数学思想方法的落实，通过一题多解、一题多变等思维活动，引导学生进行方法的比较、优化，寻求解决这类问题的规律与策略，提升学生的学科素养和关键能力．

2.3 问题研究促进思维生长

杜威曾说：“学习就是要学会思维，教育的目的不是学会知识， 而是习得一种思维方式．”数学教学不应局限于一个狭窄的课本知识领域里，应该让学生对知识和技能初步理解与掌握后，进一步深化和熟练，使其在学习中学会运用课本知识举一反三解决各类问题．为此，我们应当加强微专题研究课的教学，帮助学生把所学的知识点融会贯通，让学生在无穷的变化中领略数学的魅力，体会学习数学的乐趣．通过“四学课堂”的实践，希望学生能学会研究数学问题的方法与策略，促进思维生长．