雨洪水回灌中多分散颗粒运移-沉积特征及数值模拟

邹志科，李亚龙，余 蕾，李 伟，罗文兵，孙建东

(1.长江科学院 农业水利研究所，武汉 430010； 2.中国水电基础局有限公司，天津 301700)

1 研究背景

在水资源短缺和水环境污染的双重压力下，雨洪水人工回灌作为一种积极有效的应对方式，不仅能将雨洪水储存在含水层中以备不时之需[1-4]，而且可以缓解城市内涝和减少水污染的风险[5]。但是，雨洪水回灌过程中多分散颗粒造成的堵塞问题一直是限制回灌技术大规模应用的主要原因之一[6-9]。当含有不同粒径颗粒的雨洪水流经多孔介质(过滤介质)时， 一部分颗粒会被截留在介质表面上，一部分会在多孔介质内部运移，并通过与介质表面相互作用而沉积，从而使得过滤介质逐渐堵塞，雨洪水得到澄清和净化[10]。堵塞严重地降低了回灌系统的过滤效率和使用寿命[11]，即使通过预处理的雨洪水，仍会造成介质堵塞引发渗透系统的故障[12-13]。

堵塞作为一种宏观现象，实质是微观尺度上多孔介质中颗粒的运移和沉积。控制多分散颗粒的运移和沉积的机制复杂多样，取决于颗粒的大小[14-15]。对于较大的颗粒(> 10 μm)，重力、惯性和水动力作用是颗粒的主要沉积机制；布朗扩散是胶体(<1 μm)沉积的主要因素；对于中等大小的悬浮颗粒(1～10 μm)，以上所有机制都可能导致颗粒沉积[16]。

胶体过滤理论(Colloid Filtration Theory，CFT)和经典过滤模型被广泛应用于描述饱和多孔介质中颗粒运移和沉积过程[4]。经典过滤模型假设单分散、非絮凝的颗粒以恒定流速通过均质各向同性的多孔介质，其中暗含的颗粒一阶沉积项使得沉积颗粒的空间分布呈指数形式[17]。

粒径分布作为影响颗粒运移和沉积的重要因素之一，其对颗粒沉积影响的研究尚显薄弱。胶体过滤理论通常聚焦于粒径<1 μm 的胶体颗粒，控制胶体颗粒沉积的机制比较单一，主要是布朗随机运动，所以以平均粒径代表颗粒粒径范围[18-19]。然而，雨洪水中颗粒具有极强的多分散性，横跨了传统的胶体颗粒和悬浮颗粒粒径范围，控制颗粒运动的作用力和机制更加复杂多样，雨洪水人工回灌中多分散颗粒运移-沉积规律的揭示仍是一个具有挑战性的课题。因此，本文拟开展5种不同浓度条件下多分散雨洪颗粒人工回灌一维砂柱定流量试验，通过砂柱出口的穿透曲线和砂柱中沉积颗粒的剖面曲线刻画多分散颗粒的运移和沉积特征，应用考虑颗粒多分散性的过滤系数进行相应的数值模拟，并与常规过滤模型进行对比，物理试验数据验证了改进模型的合理性与适用性。

2 物理试验

2.1 砂柱设计

砂柱试验装置由回灌动力系统、观测系统和数据采集系统组成(图1)。动力系统由悬浮液储槽、蠕动泵和砂柱组成，观测系统主要包括压力传感器和流量计，数据采集系统包括无纸记录仪和电脑。有机玻璃柱长度为60 cm，内径为5 cm，厚度为1.5 cm。其中50 cm 的主体部分填充选定的石英砂介质，砂柱顶部安装了分散器，用以保护上部介质不受注入雨水冲刷能量的影响，砂柱底部装有0.1 mm的滤网防止石英砂颗粒的流失。

图1 试验装置示意图Fig.1 Schematic representation of the experimentalapparatus

2.2 多分散颗粒和多孔介质的特征

本试验回灌所用的多分散颗粒是刮出长江岸坡表层沉积物而收集的，然后经过不断地干燥、碾磨和机械筛分，最终高温灭菌后称重并溶于纯水中，将其配制为不同浓度的雨洪水作为回灌水源。颗粒的堆积密度和固体密度经测量分别为1.05 g/cm3和2.51 g/cm3。粒径分析结果显示，多分散颗粒的粒径范围为0.375～55.82 μm，平均粒径为8.15 μm，与实际回灌工程中发生堵塞的粒径特征保持一致[20]。

选用最常用的石英砂作为多孔介质，其结构在回灌过程中保持稳定，孔隙度0.378(±0.003)，固体密度为2.56 g/cm3。选用石英砂的d10为0.302 mm，d50为0.451 mm，d60为0.473 mm，其不均匀系数(d60/d10)为1.57<2，表明石英砂介质是均质的[4]。选择孔径为0.1 mm的滤网可以防止介质颗粒(0.3～0.5 mm)从砂柱中流出，但允许多分散颗粒(0.375～55.820 μm)的流出。

2.3 试验方案

配置5种颗粒浓度10、20、30、40、50 mg/L进行回灌试验，每个试验中注入了253个孔隙体积(number of pore volume, NPV)的雨洪水，直至介质完全堵塞。孔隙体积是指流过砂柱的累计水量和含水介质中孔隙度之积，可以消除不同回灌场景对出流穿透曲线的影响[15]。将出流通过校准好的浊度计测量浊度值。雨洪水浓度和浊度之间的相关性见图2。

图2 浊度和浓度之间的关系Fig.2 Correlation between turbidity and concentration

雨洪水回灌之前，首先进行清水回灌直至保持出流流量稳定至少1 d。进行清水回灌不仅可以实现介质的水力压实，以便进行渗透系数计算，而且能洗去介质表面的微粒，尽可能减少背景值对浊度测量的影响。回灌试验结束后，取出填充在砂柱的石英砂介质,并将其切成10等份，每等份5 cm。通过以下步骤称量颗粒的沉积量：将沉积有颗粒的介质干燥并称重，然后彻底洗涤后通过开孔为0.1 mm的滤网得到清洁的介质，将清洁的石英砂干燥并称重，洗涤前后介质之间的质量差是沉积颗粒的总质量。使用激光粒度仪对收集样品进行颗粒粒径分析。

3 数值模拟

3.1 常规模型

常规过滤模型包括颗粒质量平衡方程和颗粒沉积动力学方程。颗粒的质量守恒方程中考虑了颗粒的浓度和沉积量随时间的变化，如式(1)—式(4)所示[17]。

(1)

(2)

(3)

(4)

式中：C(L3* L-3)是悬浮液中颗粒的体积分数；z(L)是从砂柱顶部开始的轴向距离；σ(L3* L-3)是比积泥量，表示沉积颗粒的体积与多孔介质的体积之比；σm的最大值；u(L * T-1)是回灌速度，可以通过达西试验获得；t(T)是回灌时间；ε和dc分别是介质的孔隙度和平均粒径；η是颗粒的通过单个介质被捕获的概率，根据胶体过滤理论，可以通过颗粒轨迹分析计算得到[18]。

3.2 改进模型

λ0(L-1)是过滤系数，其物理意义是在1/u的时间间隔内颗粒被多孔介质捕获的概率[16]。基于单分散颗粒假设的胶体过滤理论认为λ0只是一个常数，但是当多分散颗粒在介质孔隙中运动时，具有较高捕获概率的颗粒更可能被多孔介质捕获，而具有较低捕获概率的颗粒可以运移更长的距离，或通过砂柱并在出流中被检测到。因此，多分散颗粒的过滤系数实际上沿着多孔介质变化，λ0是流径多孔介质距离的函数。改进过滤模型的过滤系数λ0(z)[21]的表达式为

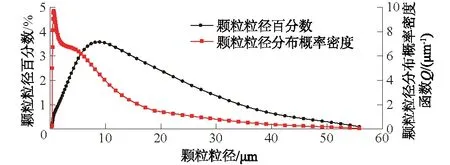
图3 回灌水源的颗粒级配曲线及其概率密度函数Q(x)Fig.3 Sand grading curve and probability densityfunction of the particle for recharge water

采用有限差分方法计算有关变量(C、σ)的数值解，设置Δt为2 min，Δz为0.5 cm。回灌上边界保持定浓度，边界条件为C(z=0,t)=C，∂C/∂z|z=L=0；回灌开始时，整个砂柱不含悬浮颗粒和沉积颗粒，初始条件为C(z,t)=0,σ(z,t=0)=0。

颗粒在介质孔隙中的沉积会导致多孔介质渗透性降低，渗透性系数通过达西公式计算(式(6))，对于长时间的回灌试验，相对渗透系数K/K0与累积沉积量呈负相关关系[22]。回灌试验的整体渗透系数的变化可以通过Kozeny-Carman模型模拟[21]，即：

(6)

(7)

式中：K为饱和介质的渗透系数(L/T)；Kt为t时刻介质的渗透系数(L/T)；ε0为介质的初始孔隙度；Qf为出流流量(L3/T)；L为砂柱填充长度(L)；A为砂柱填充横截面积(L2)；Hi、Hj测压管编号i和j的水头(L)；y和z均是沉积颗粒影响渗透系数降低的综合系数，通过曲线拟合可得y=1.05，z=1，很好地表征了多分散颗粒沉积造成渗透性降低的变化趋势。

为了对常规模型λ0和改进模型λ0(z)的5组模拟结果与试验结果进行对比，本文采用标准平均相对误差作为模型计算数据与实测结果之间误差的计算方法，其计算公式如式(8)所示。

(8)

式中：Rs是标准平均相对误差；yi、y′i分别是实测值与模拟值；ymax、ymin分别是实测值的最大值与最小值；n为数据个数。

4 结果和讨论

4.1 颗粒在多孔介质中的运移和沉积

图4显示了在不同回灌浓度下，改进模型与常规模型模拟的穿透曲线(Breakthrough Curve, BTC)的比较，常规模型利用恒定的过滤系数λ0，认为回灌初始阶段整个介质表面对颗粒具有相同的捕获能力，而改进模型考虑不同粒径颗粒具有不同的捕获概率。对于试验的整个浓度范围(10～50 mg/L)，可以观察到颗粒相似的运移特征：出流浓度随着颗粒回灌量的增加而增加。这是因为多孔介质内沉积颗粒的累积减少了进一步沉积的空间，导致颗粒沉积效率的降低，观测结果与前人结果[23]保持一致。回灌253Vp(Vp为孔隙体积)颗粒后，对于50、40、30、20、10 mg/L的颗粒浓度，相对浓度(Cout/C0，出流浓度与初始浓度的比值)分别达到82.3%、80.0%、72.4%、61.4%、48.6%。

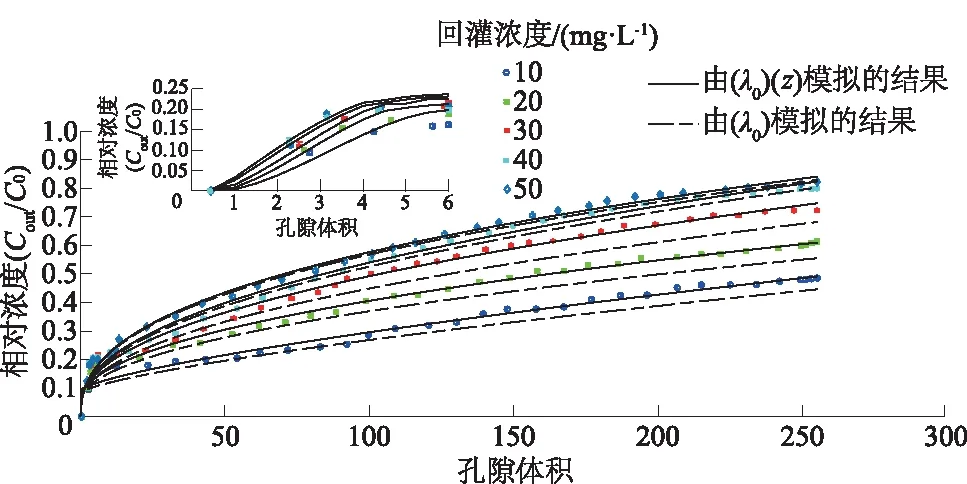
图4 常规模型(λ0)和改进模型(λ0(z))模拟的穿透曲线结果对比Fig.4 Comparison of breakthrough curves (BTCs) ofthe particles (symbols) from conventional model (λ0)and modified model (λ0(z))

回灌过程开始时，由于介质间沉积点位足够多，已沉积的颗粒并不妨碍后续颗粒在介质孔隙中的沉积;此外，在低速时，水动力不足以阻止沉积和剥离已沉积在多孔介质表面的颗粒[24]。在恒定流速回灌的条件下，孔隙间颗粒的累积会降低介质的孔隙度并导致孔隙流速的增加，因此增强了沉积颗粒的水动力作用，使得颗粒的沉降效应和重力效应减弱。水动力起着双重作用，即提高颗粒的运移速率并可能引起之前沉积颗粒的重新释放[25]。因此，出流中的颗粒浓度随时间增加。试验过程中还观察到，BTC受入流浓度的影响，在一定的孔隙体积下，较高的入流颗粒浓度导致较高的出流浓度，原因是多孔介质孔隙内的沉积速率取决于颗粒的浓度，较高浓度颗粒的沉积速率要快于低浓度颗粒的沉积速度[14]。

出流相对浓度计算结果的标准平均相对误差的比较如表1所示。由表1可知，改进模型模拟的5组结果的标准平均相对误差Rs最大值为0.021，最小值仅为0.003，平均值为0.013；常规模型的5组试验的标准平均相对误差Rs最大值为0.083，最小值为0.024，平均值为0.046。如果以5%的误差范围作为标准，两个模型都可以较好地模拟出流浓度的过程曲线。

表1 出流相对浓度计算结果的标准平均相对误差比较Table 1 Comparison of standard mean relative errors ofBTCs between conventional model and modified model

4.2 沉积颗粒的空间分布

仅BTC不足以准确表征颗粒在饱和多孔介质中的运移和沉积行为，沉积剖面曲线的形状是表征颗粒沉积机制的关键指标[26]。图5显示了不同回灌浓度下改进模型与常规模型模拟的最终沉积剖面。所有不同回灌浓度的最终沉积剖面曲线的形状都相似，沉积剖面曲线具有2个不同特征的区域：沉积剖面曲线上部分斜率较陡，曲线下部分斜率趋于平缓，呈现超指数分布。试验观察到的超指数分布特征在所试验的整个颗粒浓度范围内都很明显。试验结果表明，在整个多孔介质中，颗粒的沉积剖面曲线形状呈现高度非均匀分布，尤其是在多孔介质的顶部(z≤10 cm)，但随着深度的增加而降低。

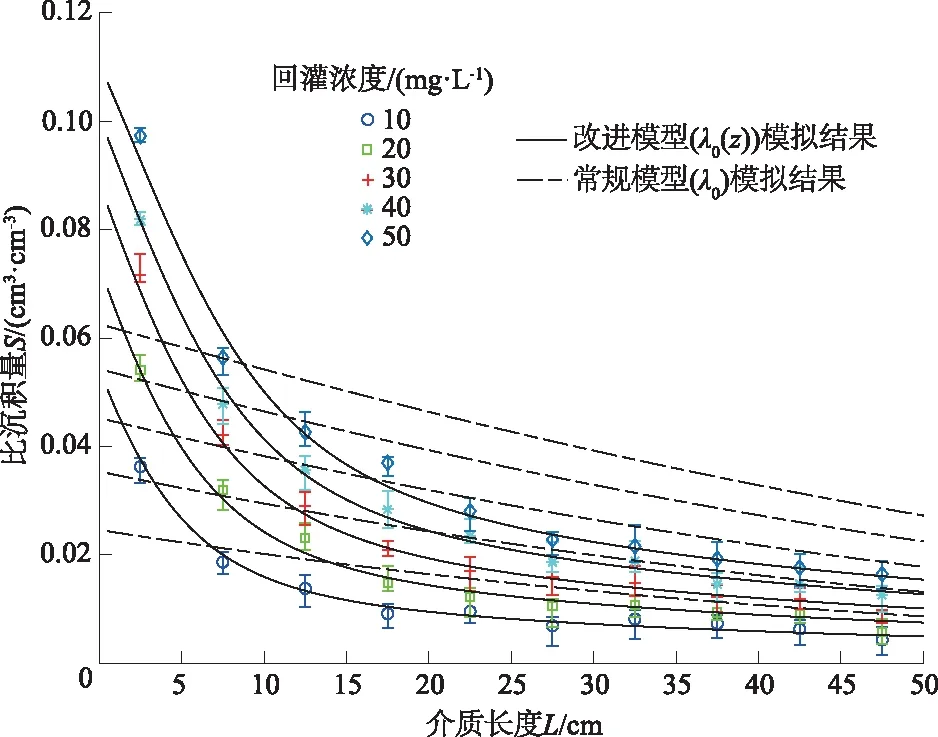
图5 常规模型(λ0)和改进模型(λ0(z))模拟的沉积剖面对比Fig.5 Comparison of retention profiles of the particlesbetween conventional model (λ0) and modified model(λ0(z) )

对于回灌浓度C0=50 mg/L，多孔介质的顶部沉积量占总沉积量的近40%，而较深的部分对颗粒沉积的贡献较小。在给定深度，沉积量随回灌颗粒浓度的增加而增加。但是，常规模型无法准确地刻画多分散颗粒沉积的超指数分布，因为常规模型预测与试验观察到的结果(尤其是在多孔介质的上部)之间有很大的差异。

最终沉积剖面计算结果的标准平均相对误差的比较如表2所示。由表2可知，改进模型模拟的5组结果的标准平均相对误差Rs最大值为0.031，最小值仅为0.009，平均值为0.019；常规模型的5组试验的标准平均相对误差Rs最大值为0.35，最小值为0.14，平均值为0.23，而且标准平均相对误差随回灌浓度的增加而增大。同样以5%的误差范围作为标准，改进模型可以很好地模拟测试浓度范围内的沉积剖面曲线，而常规模型造成很大的预测误差。结果表明常规模型不能刻画多分散颗粒沉积的超指数分布特征。

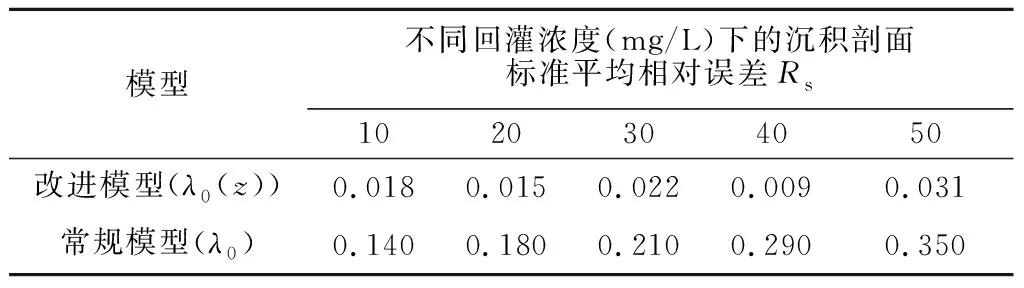
表2 最终沉积剖面计算结果的标准平均相对误差比较Table 2 Comparison of standard mean relative errorsof retention profiles between conventional model andmodified model

表3显示了回灌颗粒的质量平衡：在出口处回收的颗粒的质量百分比(Meff)，每个部分的沉积质量百分比，总沉积质量百分比(Mp)，(Mtot=Mp+Meff)。表3表明，约占回灌总质量20%～30%的颗粒被截留在介质上部0～10 cm(标号1和2)的部分，而砂柱下段20 cm的介质长度(标号7—10)只截留了约占总量8%～14%的颗粒，该结果从颗粒的质量平衡角度证明了多分散颗粒堵塞的特征：多分散颗粒呈现高度非均匀沉积特征，并大部分颗粒沉积在多孔介质的表层。

表3 回灌颗粒的质量平衡Table 3 Mass balances of injected particles

4.3 沉积颗粒的粒度分布分析

试验过程中分别测量了进水口和沉积颗粒的级配曲线，以进一步阐明控制多分散颗粒沉积的机制。图6描述了30 mg/L颗粒回灌试验结束时各部分沉积颗粒的级配曲线。由图6可知沉积颗粒的级配曲线沿着介质深度而变化。

图6 回灌浓度30 mg/L的沉积颗粒粒径分布Fig.6 Characterization of the particle-size distribution(PSD) of the retained particles in different sections in thepresence of a recharge concentration of 30 mg/L

由于颗粒不均匀地沉积在多孔介质中，中值粒径d50的观察值从顶部(z≤10 cm)的22.59 μm减小到底部(40≤z≤50 cm)的8.12 μm。此外，顶部捕获的颗粒粒径范围几乎与回灌水源中颗粒粒径范围(0.375～55.82 μm)相同，而底部介质捕获的粒径范围(0.375～22.59 μm)远小于回灌水源中颗粒粒径范围。颗粒的级配曲线表明，较大的颗粒主要在砂柱入口附近被介质表面捕获，导致底部介质只能捕获较小的颗粒。颗粒粒径与介质的平均粒径(451 μm)之比(dp/dg)为0.000 83～0.124。对于粒径>2.26 μm的颗粒，该比值等于0.005(筛滤作用的阈值)[27]，回灌雨洪水中79.4%的颗粒粒径>2.26 μm，这证实了筛滤是试验中介质堵塞的主要机制，其余4组回灌浓度呈现相同的变化规律。

4.4 渗透系数的时空变化

颗粒的不均匀沉积不可避免地导致多孔介质渗透性的降低，因为渗透性与介质孔隙度直接相关[21]。多分散颗粒的不断沉积也会造成均匀孔隙通道变窄甚至堵塞孔隙，颗粒堵塞最直观的现象是测压管水头损失变大，介质渗透能力降低[28]。

结果表明在回灌试验结束后，最初是均一渗透系数的含水介质沿着砂柱变得高度不均匀。这种不均匀分布随着浓度的增加而增加。所有浓度下的渗透系数曲线显示出相同的趋势，在给定位置，当颗粒浓度较低时，渗透系数的下降幅度较小。渗透系数在入口附近下降的幅度最大，然后随着深度增加而接近初始渗透系数K0，在相同的颗粒浓度(C0=50 mg/L)的情况下，顶部(z≤5 cm)的渗透系数降幅达到52%，而底部的渗透率降幅仅为13%。图7(b)显示了不同浓度下砂柱整体渗透系数的变化。随着回灌颗粒浓度的增加，曲线变得更“陡峭”，即相对渗透率下降越快。对于50 mg/L的回灌浓度，仅回灌50个孔隙体积左右，渗透系数便下降了30%。相对渗透系数随时间下降，但下降速度通常随时间变得缓慢，在试验结束时趋于恒定值[29]。砂柱整体渗透系数的变化主要受介质表层渗透系数的变化影响，随着回灌量的增加，更多的颗粒堵塞在多孔介质的孔隙内，渗透系数的降低往往是堵塞直接的表现形式[9]。

图 7 相对渗透系数K/K0的变化Fig.7 Evolution of normalized permeability K/ K0

渗透性能的不均匀下降与颗粒沉积的空间分布(图5)是一致的。在整个试验过程中，Kozeny-Carman模型模拟结果与试验观察到的数据之间具有良好的一致性，表明该模型对整体渗透系数变化趋势具有较好的预测性。模拟结果也证实了渗透系数的降低主要受颗粒累积量的影响。回灌的雨洪水颗粒浓度对渗透系数降低具有间接影响，因为它们会影响沉积颗粒的量和空间分布。

5 结 论

在雨洪水的人工回灌研究中，堵塞问题是不可避免的，然而雨洪水中颗粒粒径的多分散性导致其不同于传统胶体颗粒的运移-沉积特征。通过物理试验和数值模拟，探讨了雨洪水回灌中多分散颗粒运移-沉积特征，并得到了以下结论：

(1)多分散颗粒的沉积剖面是呈现“上陡峭，下平缓”的超指数分布，并且浓度越高，超指数分布曲线的斜率越大，大颗粒的筛滤作用是产生超指数分布的主要原因，常规模型虽然可以较好地模拟出口的穿透曲线，但是无法准确刻画多分散颗粒的超指数分布沉积剖面。

(2)多分散颗粒的过滤系数λ0(z)是关于距离递减的函数，由捕获概率η(x)和颗粒分布的概率密度函数Q(x)共同决定，在流向上的变化实质上是由颗粒的概率密度函数在流向上的变化引起的；改进模型可以更好地刻画多分散颗粒在介质中的堵塞特征，多分散颗粒的非均等沉积造成了超指数沉积剖面的形成。

(3)多分散颗粒的沉积直接降低了多孔介质的渗透性，Kozeny-Carman模型可以估计整体渗透性能降低的变化。局部渗透系数和总渗透系数的降低均表明沉积物分布不均匀。