钢混组合梁桥的滑移、曲率及挠度分析

朱万勇

（河北省交通规划设计院，河北 石家庄 050011）

钢混组合梁将混凝土板和钢梁组合成整体，充分发挥了混凝土的抗压性能和钢梁的抗拉性能，实现了受力合理和节约材料的目标，在工程中的应用日趋广泛。根据剪力连接程度的不同，将钢混组合梁分为完全剪力连接和部分剪力连接。由于混凝土的干缩、徐变等种种原因，在结合面上往往会出现影响整体受力的混凝土开裂、错位现象。在满足承载能力和变形要求条件下采用部分剪力连接设计，可以简化建造工艺方便施工，节省造价，是经济合理的一种构造形式。但是用部分剪力连接设计的组合梁桥不可避免地会造成钢梁与混凝土交界面处变形的不一致，产生相对滑移，加大了梁内各点的曲率，增加了桥梁的挠度。

一、计算图式及基本假定

本文以受均布荷载的部分剪力连接组合简支梁为研究对象，计算图式如图1所示。为了简化计算，特作如下假设：钢及混凝土均为理想线弹性材料，计算中弹性模量为常量；钢梁与混凝土板具有相同的曲率；钢梁与混凝土板之间剪力的传递仅通过剪力连接件来实现，忽略两者之间的摩擦作用；混凝土板与钢梁之间不发生掀起现象，混凝土板下缘与钢梁上缘的竖向距离无穷小。

图中S为钢与混凝土结合面处的相对滑移量，ds/dz为钢与混凝土结合面处的滑移应变，θ为截面转角，φ为截面曲率。

二、弹性控制微分方程的建立及求解

（一）弹性控制微分方程的建立

钢梁的应变能为：

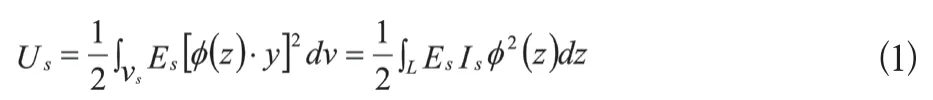
式中：Es为钢的弹性模量；为组合梁的曲率函数；其中，As为钢梁横截面。

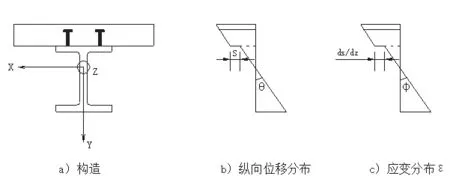
图1 计算图式

混凝土板的应变能为：

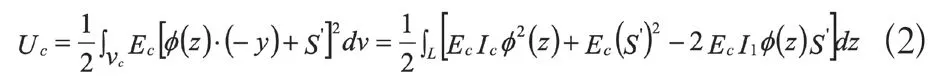
式中：Ec为混凝土板的弹性模量；S(z)为钢与混凝土结合面的相对滑移量，以下简记为S；即ds/dz为钢与混凝土结合面的滑移应变。其中为混凝土板横截面。

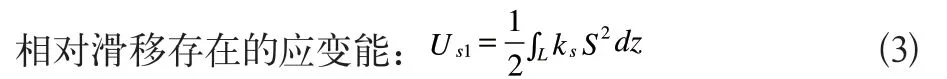
式中：ks为剪力连接件沿梁轴线单位长度相对滑移一个单位的剪切刚度，是影响混凝土板和钢梁之间剪力连接强度的重要因素。

对于均布荷载作用下的简支梁，外荷载势能为：

式中：q为作用于简支梁的均布荷载；ω 为简支梁的竖向挠度。于是，全梁的总势能为：

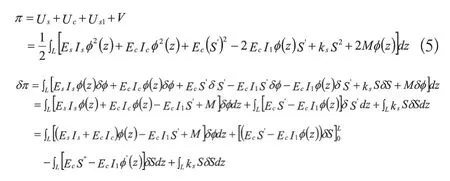
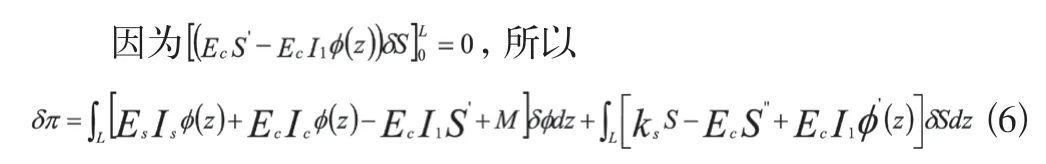
取δπ=0得：

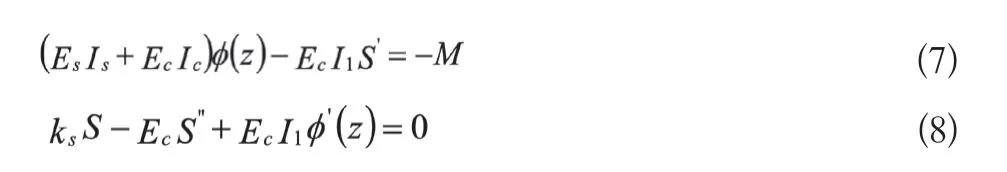
（二）控制微分方程的求解

1.部分剪力连接组合梁的求解

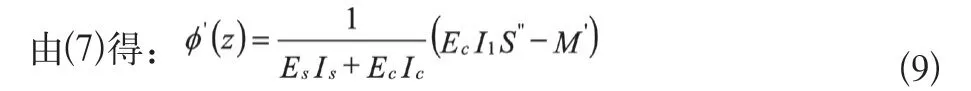
将(9)代入公式(8)得：

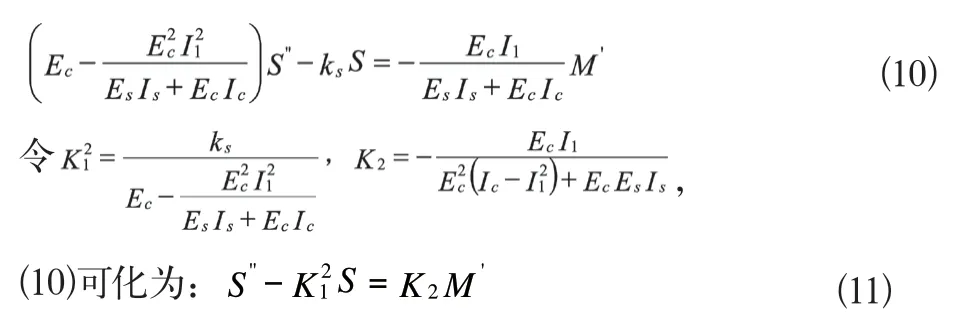
由于为均布荷载作用下的简支梁，所以

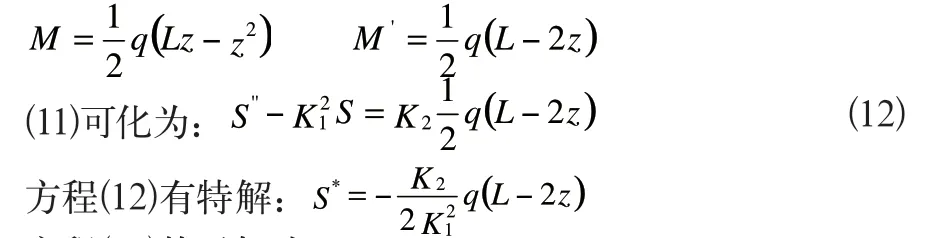
方程(12)的通解为：

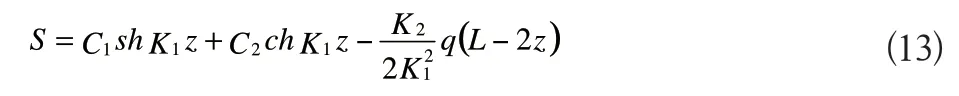
对式(13)求导得

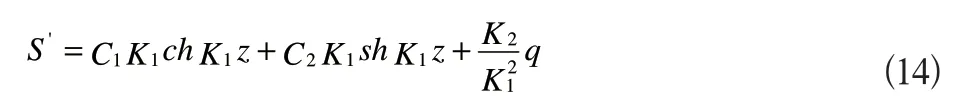
将式(14)代入式(7)得：

由以上推导即可得钢与混凝土结合面的相对滑移量S和组合梁的曲率：

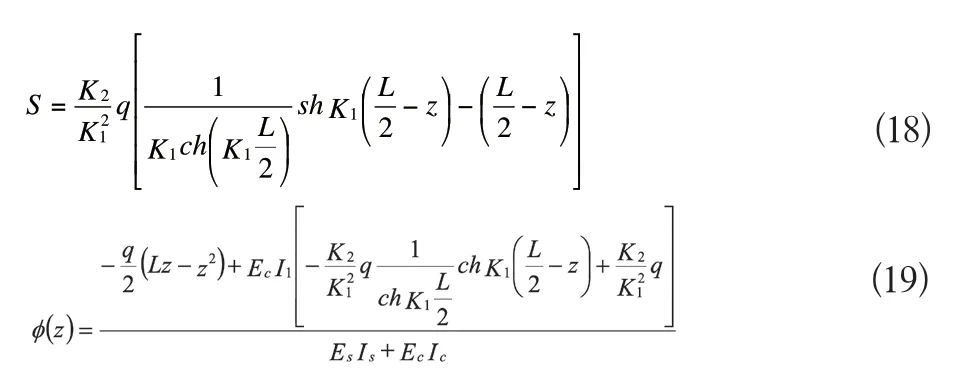
对式(18)求导，可得出部分剪切连接组合梁滑移应变ds/dz，即S'的表达式：

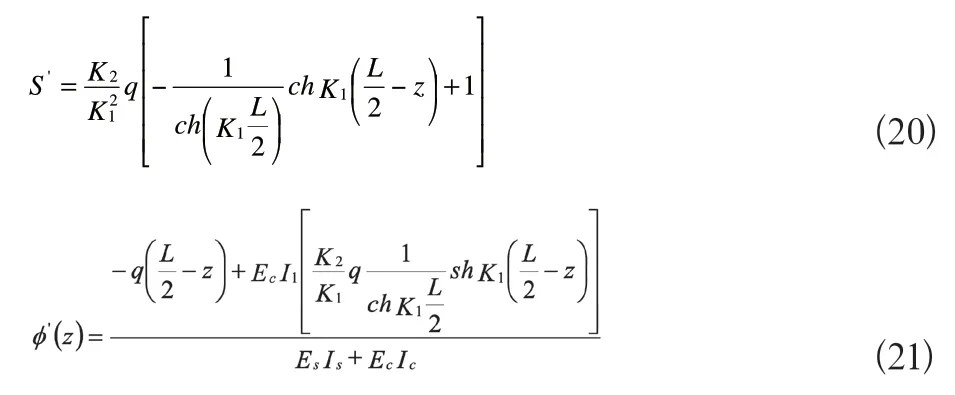
2.叠合梁的求解

当Ks=0时，即为叠合梁的情况，此时K1=0，由式（7）和式（8）并结合边界条件可得叠合梁的结合面相对滑移量S和叠合梁的曲率

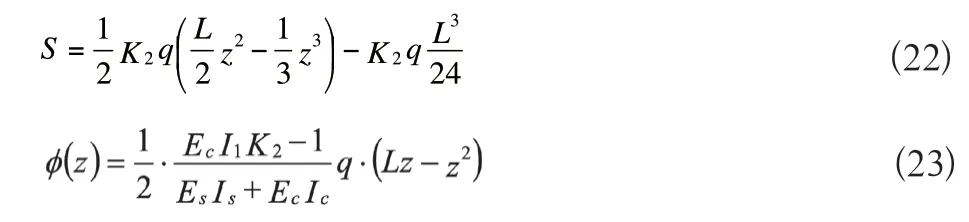
对式(22)求导，可得出叠合梁滑移应变ds/dz，即S'的表达式：

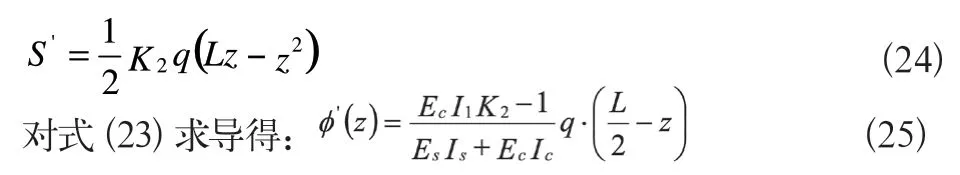
三、相对滑移、滑移应变以及曲率的分析

当Ks→∞时，即为理想的完全剪切连接组合梁的情况，此时K1→∞，由式（18）可知此时S→0 。

由式（20）和式（24）可知，无论是部分剪力连接组合梁还是叠合梁在区间上S'均为关于z的一个增函数，所以，无论组合梁的剪切连接程度如何，在z=0处，S'达到最小，在处，S'达到最大。

本文运用剪力连接件沿梁轴线单位长度相对滑移一个单位的剪切刚度ks综合反映了影响组合梁交界面处剪力传递的所有因素。

四、组合梁的挠度精确解

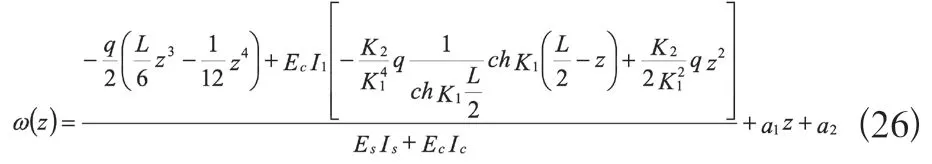
由边界条件z=0，ω(0)=0；z=L，ω(L)=0，可得：

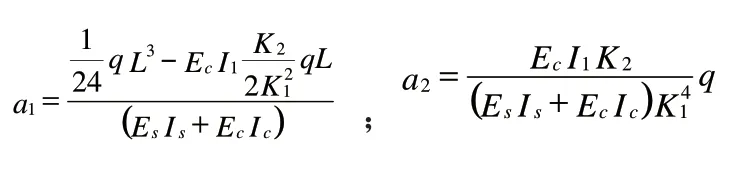
由以上各式可得组合梁的精确挠度解为：

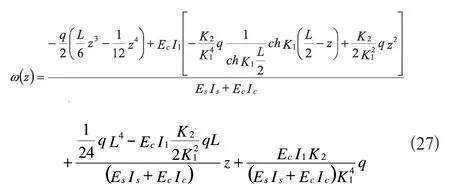
五、组合梁的挠度分析

将式（23）积分两次，并由边界条件 ω(0)=0，ω(L)=0可得叠合梁的挠度值：

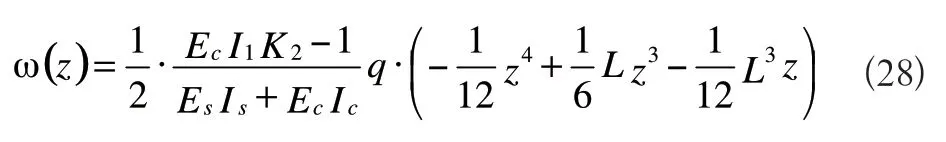
六、结语

根据以上分析，可得到如下结论：一是滑移应变ds/dz随着剪切刚度Ks的增大而减小；二是无论组合梁的剪切连接程度如何，在支点处，滑移应变ds/dz达到最小，在跨中处，滑移应变ds/dz达到最大；三是组合梁交界面处的相对滑移量在支点处取最大值，所以在组合梁的设计中应加强支座处的剪力连接程度；四是无论组合梁的剪切连接程度如何，在跨中处，组合梁截面曲率达到最大；五是公式(27)在计算组合梁的挠度时，同时考虑了滑移效应和剪切连接强度的影响，较为合理。