黄金分割法在矿井通风系统设计中的应用

郭孟嘉，张 金，秦 龙

（铁法能源公司大隆矿，辽宁 调兵山 112700）

引言

地下采矿与矿井通风网络结构的建设和维护有关，矿井通风网络的分支可能包括连接主风机子网络的分支。根据矿井通风理论，可将其划分为多种分支，这些分支中的气流是与用风有关的[1]。除其他外，煤矿业的重组过程还可能导致采矿厂的合并及其通风网络结构的变化。考虑到采矿厂工作人员的安全，重要的是要确保足够的空气量和气流速度[2]。

1 矿井通风网络中的强制送风

强制空气分配问题包括向矿工工作场所提供规定数量空气的要求，同时需考虑到法律规定和自然灾害[3]。已知的是矿井通风网络的结构、某些通风支路的已知风量和所有支路的空气阻力；未知的是与主通风机相关的参数，如压力和风量、气流调节器的设置及剩余分支的气流[4]。

在通风网络只有一个主风机的情况下，引入气流调节器设定值为零的关键路径。这样的操作可以确定有效功率最低的主风机的最佳参数。在通风网络中，由平衡定律导出方程的个数等于未知值的个数。有必要提出一种新的方法使配风机的有效功率最小化，从而找到最佳的配风方式[5]。

其允许将气流“引导”到每个风扇，从支线经直采区和功能室流出的全部空气可按不同比例分布在支线的风机之间。每个分布不仅在分支中的气流方面不同，而且在风机压差和调节器的设置（如调节塞的空气动力阻力）方面也不同。因此，找到这样的空气分布方法能使主风机的总有效功率尽可能减小。

2 黄金比率分割法

在具有两个主风机且子网相互连接的通风网络中，假设在整个截面内具有起飞点（如直接开采区和功能室）的每个分支中存在给定气流，允许实现满足平衡定律的无限数量的空气分布。综上，在这种情况下，未知值的数量超过由平衡定律得出的方程的数量。如果选择了反树状型的分支，则可以为这些分支强制独立的气流条件。但是，由于排气轴中的气流方向已知，用风扇强制进入支管的气流必须满足公式（1）规定的条件。

式中：VW为主风机的气流；Vpc为所有截面分支中的气流总和。

对于VW风机的不同强制气流值，实现了不同的气流分布，其特点是主风机的不同参数，包括有效功率。为了确定主风机的有效功率，假设为最小值的空气分配，可以应用数学上已知的黄金比率法。在所涉及的问题中，目标函数采用公式（2）中所示的形式。

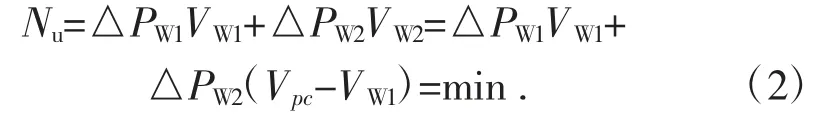
式中：Nu为主风机的总有效功率；VW1，VW2为风机1和风机2 处的气流流量；△PW1，△PW2为风机1 和风机2 所需的压差。

极限条件由第一和第二基尔霍夫定律的方程组成。所研究的目标函数和极限条件都是凸函数。因此，可以应用黄金比率法寻找公式（2）中所示函数的最小值。应注意的是，在风机1 处强制气流后，可使用强制气流的风机压差（△PW1，△PW2）特性值来确定强制气流分布。因此，公式（2）中给出的目标函数是一个自变量（风机1 处的气流）的函数。此函数的形状如下页图1 所示。

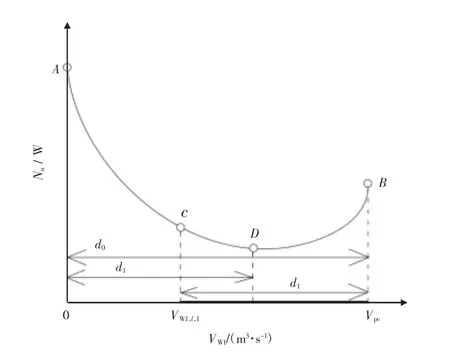
图1 黄金比率法在通风网络中的应用

有效功率最小的一次间隔的长度（d0）等于具有起飞点的分支中气流流量的总和（Vpc）。该间隔的极值点对应于空气分布，其中通过风机1 的气流为0（点A）或整个空气（Vpc）通过风机流向地面（点B）。由于目标函数的性质，在其中一个点得到了以风机总有效功率最大为特征的气流组织。黄金分割法包括在随后的迭代中缩小主要间隔。最初，在每个迭代中，使用公式（3）计算间隔的长度（di），k 为迭代系数。间隔将在该迭代完成后获得。

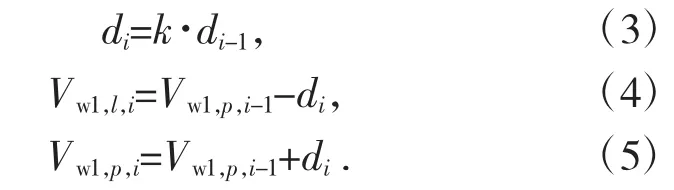
对于以这种方式强制的主风机气流，计算新风区和用风区的空气分布[6]。接下来，应计算调节器的设置和主风机的参数，包括其总有效功率。该方法的另一个步骤是比较在先前确定的空气分布（与C 点和D 点相对应的空气分布）下获得的风机有效功率的总值。比较中可能出现以下两种情况：

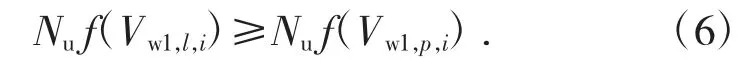
在这种情况下，间隔在左侧收紧。风机的最小有效功率将出现在C 点和B 点投影之间新形成的间隔。第二种可能的情况由公式7 给出：

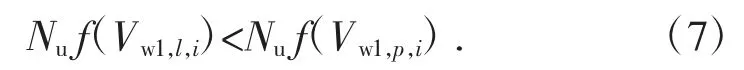
在这种情况下，间隔在右侧收紧。在这种情况下，新的间隔将位于点A 和D 的投影之间。收紧间隔后，从使用公式（3）计算间隔长度开始进行另一次迭代。进一步的过程类似于第一次迭代。当不确定度间隔的长度小于允许值时，计算完成[7]。

3 计算示例

图2 给出了A 煤矿通风网络的典型图，其中使用黄金分割法对强制空气分配进行了优化计算。通风网络由5 个送风点组成，包括4 个直接开采区和一个功能室。在分配点之前的支管中，气流调节器以调节塞的形式安装。主通风机位于分支12—14 和13—14 中。该网络包含连接W1和W2子网的气流分支9—10 和9—11。

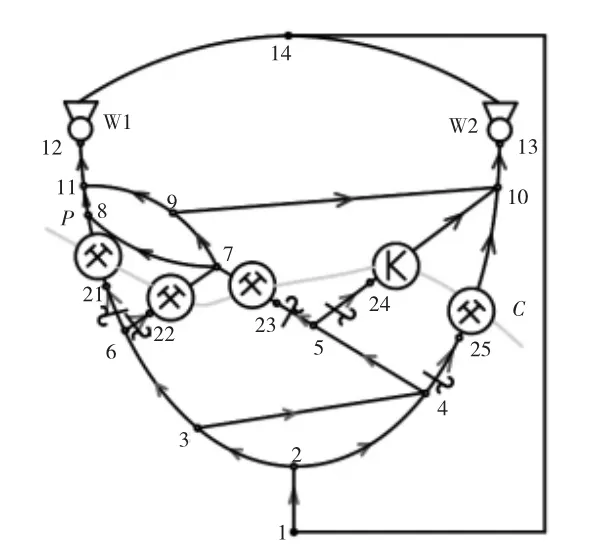
图2 矿井通风网络的标准图

A 矿通风网络包括19 个节点和26 个支路。因此，这个网络的圈数是8。因此，26 个独立的方程式是可能的，包括18 个由第一平衡定律得出的方程式和8 个由第二平衡定律得出的方程式。未知值为27，包括21 个分支的气流、4 个调节塞的气动阻力、2 个主风机所需的压力。因此，得到的方程组是超定的[8]。

表1 给出了部分有空气切断器支流的相关信息。

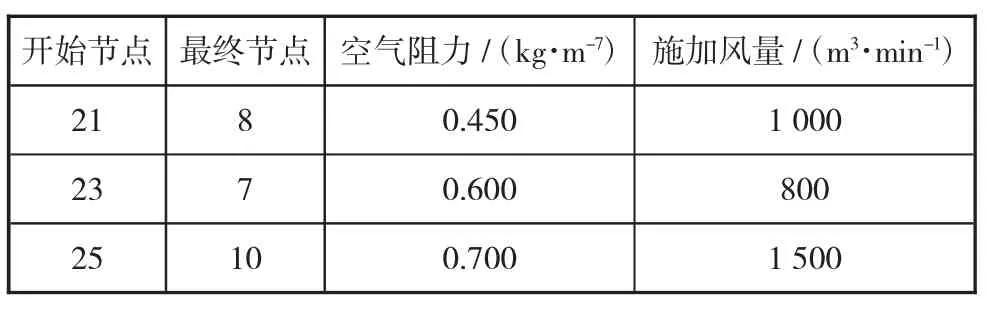
表1 有空气出口的支流特性

表2 给出了部分W1风机在3 090.17 m3/min 强制气流条件下的强制气流分布计算结果示例。

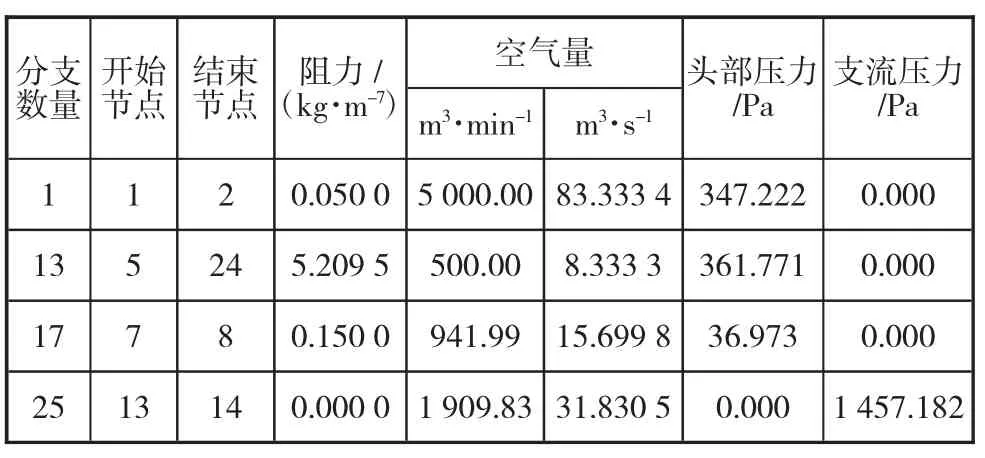
表2 矿井通风网络中的强制送风

经过迭代，图3 显示了W1和W2风机的总有效功率与W1风机的强制气流之间的依赖关系。

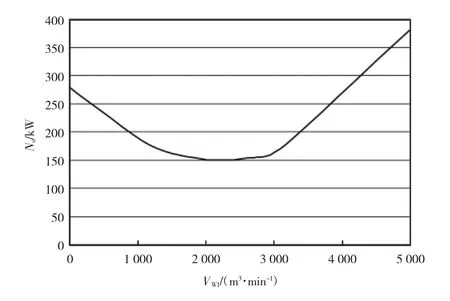
图3 风机总有效功率与W1 风机强制气流之间的关系

4 结论

在具有两个主通风机的通风网络中，子网络由一个分支互连，满足强制送风要求的解的数量是无限的。在这些解决方案中每一个的情况下，在通风网络分支中的特征空气分布在包括其有效功率在内的主风机参数值方面是不同的。为了确定以主风机总有效功率的最低值为特征的空气分配变量，可以应用本文提到的基于黄金分割法的算法。