基于小波分析的阿克苏河下游气候特征研究

蒋军新，刘新华，宋 亮

(1. 塔里木河流域阿克苏管理局，新疆 阿克苏 843000；2.华中科技大学土木与水利工程学院，湖北 武汉 430074)

干旱区由于气候环境相对恶劣，水资源缺乏，生态环境脆弱，更加需要平衡人类生产生活的要求与环境保护的关系。因此在全球气候变化的大背景下，对干旱区环境因素的变化趋势研究十分重要[1-3]。塔里木盆地是我国典型的干旱区域，年降水量少，潜在蒸发量大，以位于该区域的阿克苏河下游为对象，进行降水和气温的周期性变化研究有助于分析区域水汽状况，对于干旱区绿洲环境气候演变趋势的研究有着重要意义。

1 研究方法

1.1 数据来源

数据来源于阿克苏河下游的阿拉尔气象站1980—2005年逐月降水和气温数据。为了便于对数据趋势变化进行观察和分析，分别对两组数据进行标准化处理和3 a滑动平均的计算。并分别使用Morlet小波分析及小波相干法进行降水与气温数据的周期性和一致性研究。

1.2 方法计算

(1)数据标准化。标准化的计算如下式(1)～式(3)：

(1)

(2)

(3)

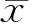
(2) Morlet小波分析。小波分析是应用广泛的时频分析工具，其基本原理是通过小波基的伸缩变换，研究信号各尺度层次上的信息，从数据信号中提取时间(空间)和频率两种信号，时间和频率形成的窗口面积是不变的，但形状可以根据不同的数据发生改变，由概貌序列研究信号的基本概貌，由细节序列研究信号的波动细节，能够准确发现数据的突变点，将数据中的奇异信息展现出来，可以对数据进行阶段性分析[4]。其数学表达式见式(4)：

(4)

式中：Wf(a,b)为小波系数；a为伸缩因子；b为平移因子；t是时间；f(t)为任意平方可积函数,即研究对象的时间序列；φ(t)为一个基本小波函数；φ*(t)为共轭函数。

本文采用Morlet小波为母小波。基于Morlet小波的基本形式，由小波变化方程计算得到小波系数和小波方差。小波系数实部等值线图可用来反映研究对象不同时间尺度的周期变化及其在时间上的分布，以此来判断不同时间尺度上的未来变化趋势；小波方差可用来反映信号能量随时间尺度的分布情况，以此来确定信号中不同种尺度变化的强弱以及信号变化的主周期。通过小波分析法对阿克苏河下游的月降水和月气温进行各时间尺度的周期性检测。

(3) Morlet小波相干。本文使用MATLAB中具有的wcoherence函数对气温和降水数据进行小波相干分析，探究两者间的变化关系。

2 阿克苏河下游降水量和气温变化分析

2.1 趋势分析

图1为经过标准化处理后阿克苏河下游1980—2005年间的年降水量变化趋势图。经计算分析，阿克苏河下游地区年平均降水量为1.49 mm。可以看出3 a的滑动平均值大体上呈现“由多到少再到多”的变化趋势。降水量最高的年份是1998年，降水量最低的年份是2001年。降水量整体呈微弱的减少趋势，减少率为0.01 mm/10 a。

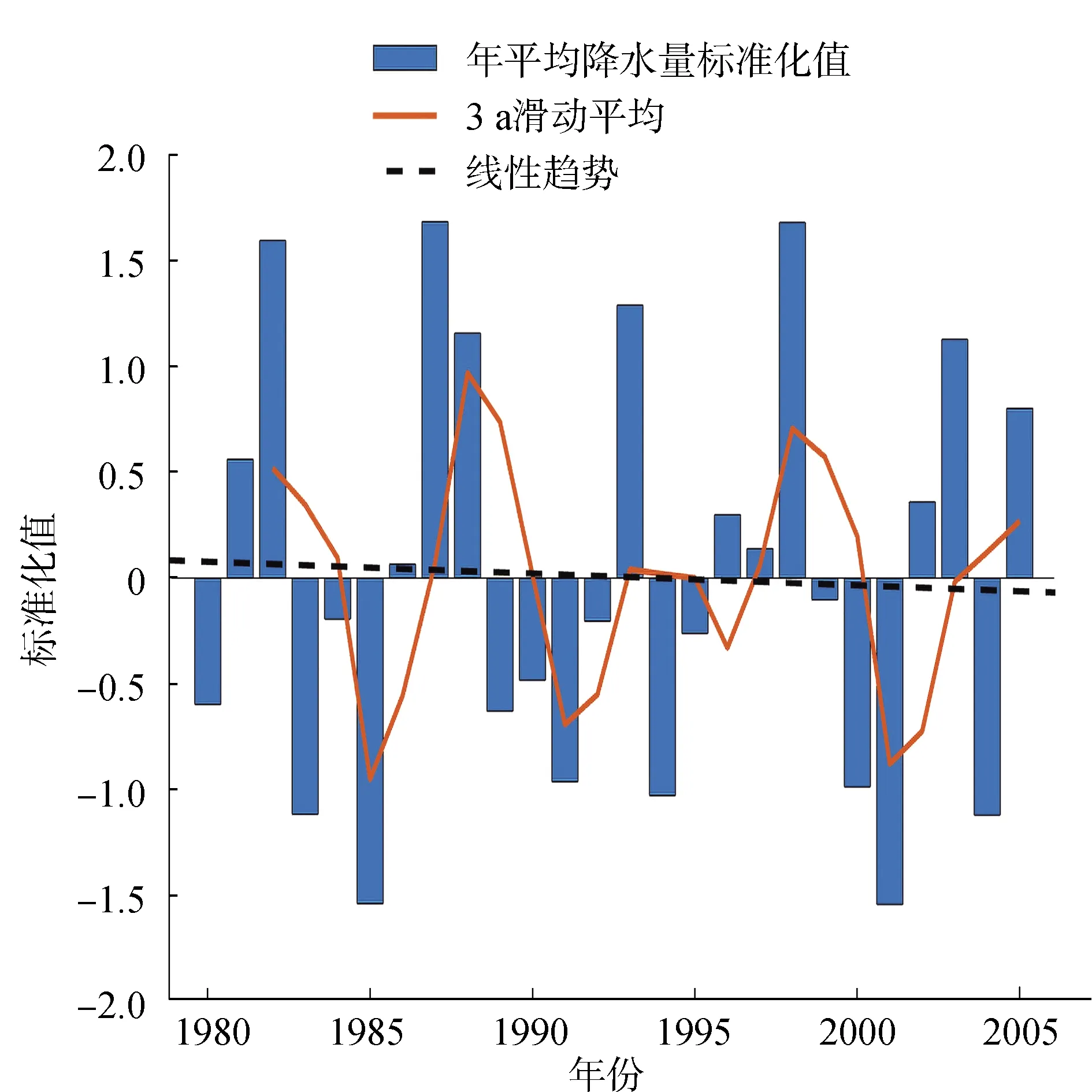
图1 阿克苏河下游1980—2005年降水量变化趋势

图2为经过标准化处理后阿克苏河下游1980—2005年间的年气温变化趋势图。阿克苏河下游地区年平均气温为10.82 ℃。气温最高年是2004年，最低年是1996年。气温整体呈现微弱的上升趋势，增加率为0.1 ℃/10 a。

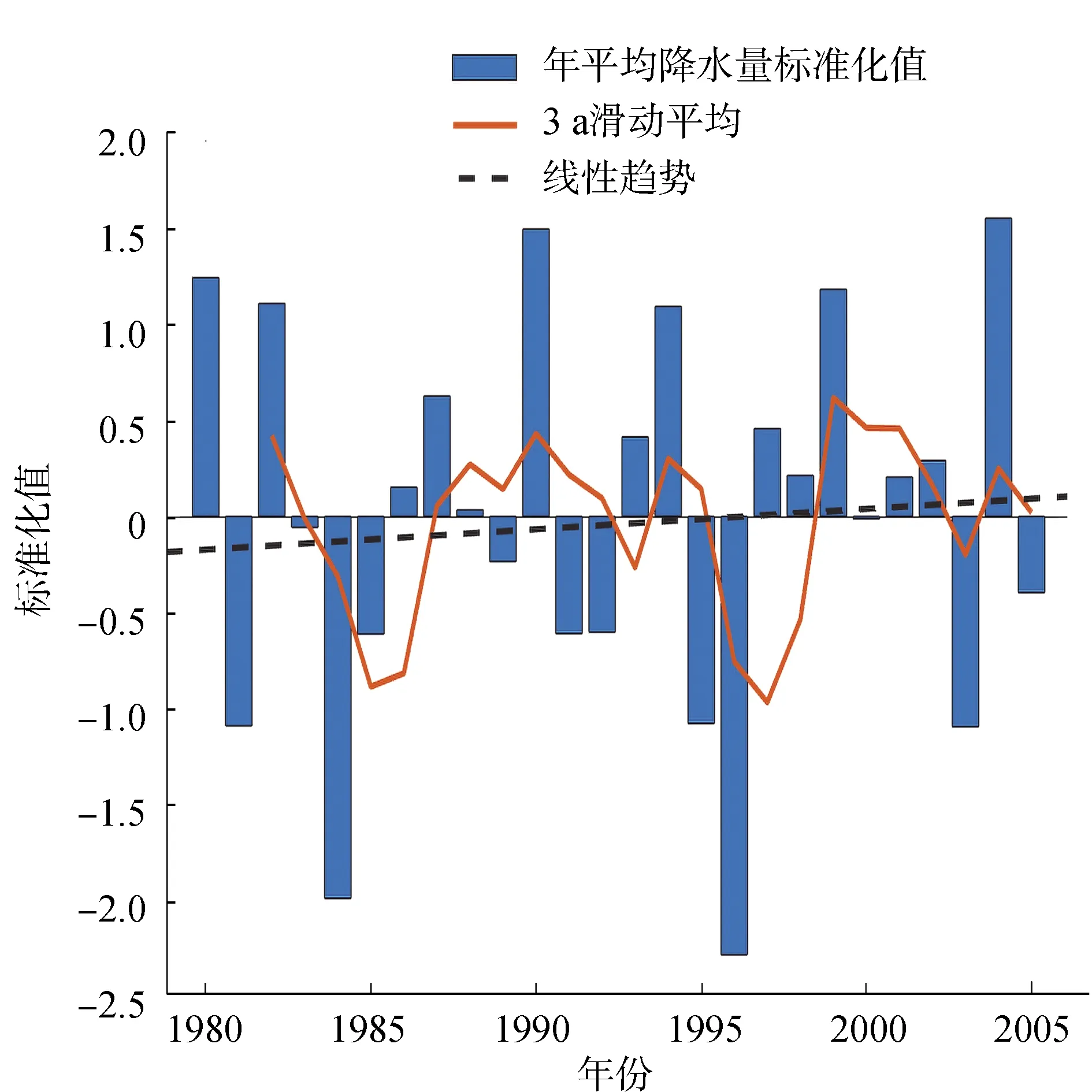
图2 阿克苏河下游1980—2005年气温变化趋势

2.2 周期分析

2.2.1 降水量小波分析

图3(a)绘制了阿克苏河下游阿拉尔气象站1980—2005年降水量Morlet小波模平方值的时频变化，从图中可以看到降水量的周期性在不同年份与时间尺度的强弱分布。图3(b)是降水量小波实部值图，图中负值代表降水量偏低，即较干旱的时期；正值代表降水量偏高，即较湿润的时期，0值表示干湿期的交替处，反映了在不同时间尺度下，研究区所处的干湿态势。图3(c)是降水量小波方差曲线，能直观展示降水量在整个研究期内不同周期大小的强弱关系。

图3 降水量小波分析

阿克苏河下游降水量的变化周期主要是0.5～1.0 a、4.0～8.0 a和16.0 a。其中0.5～1.0 a的周期性主要发生在1990—1992年、1994—1996年、2002—2005年；4.0～8.0 a的周期性在整个研究期内最为强势，发生在1981—2005年；16.0 a的周期性横贯了1980—2005年，从这个时间尺度上看，研究期被分为两个“冷-暖”周期，每个周期的持续时间约为10.0 a。

2.2.2 气温小波分析

图4(a)绘制了阿克苏河下游阿拉尔气象站1980—2005年气温Morlet小波模平方值的时频变化，从图中可以看到气温的周期性在不同年份与时间尺度的强弱分布。图4(b)是气温小波实部值图，图中负值代表气温偏低，即较寒冷的时期；正值代表气温偏高，即较温暖的时期，0值表示冷暖期的交替处，反映了在不同时间尺度下，研究区所处的冷暖态势。图4(c)是气温小波方差曲线，能直观展示阿克苏河下游气温在整个研究期内不同周期大小的强弱关系。

图4 气温小波分析

阿克苏河下游气温的变化周期主要是1 a、2～4 a和8～16 a。其中1 a的周期性主要发生在1982—1986年和2000—2005年；2～4 a的周期性几乎遍布整个研究期；8～16 a的周期性主要发生在1980—2001年，从这个时间尺度上看，1983—1997年的气温依次出现“少-多-少”的变化形式。

2.3 一致性分析

将小波相干应用于降水量和气温的时间序列数据，绘制阿克苏河下游26 a来降水与气温之间的小波相干性图像。小波相干一般反映序列间周期性“变化趋势”的一致性，但不直接反映变化周期的强度关系[5]。构造小波相干，发现显著的相干关系，并在时频空间中显示相对相位。向右箭头表示它们具有相同的相位，向左则呈负相关关系，箭头如果偏上或者偏下则说明其中一组数据的变化相对于另一组数据具有超前或者滞后效应。由于数据为月尺度，指定采样间隔为一年的1/12来显示以年为单位的时间尺度(纵轴)。同时使用默认的相位显示阈值0.5，因此它只在相干性系数大于或等于0.5的地方显示相位箭头。

图5绘制了阿克苏河下游气温和降水量的小波相干图，其中浅色区域为相干性系数相对较高的区域，深色为较低区域，白线内的部分为通过95%显著性检验的部分，白线以外的部分可信度较低。可以看出，降水和气温的小波相干性显著周期为1 a左右，分布在整个研究时段。0.25～0.50 a时间尺度的小波相干分布较为零散，没有过多的参考价值。由于1 a周期的箭头指向右方，说明阿克苏河下游降水和气温具有正相关关系，是雨热同期的。

图5 降水与气温小波相干图

为验证上述结论，本文对阿克苏河下游降水与气温进行了分位数回归并绘于图6，右侧的分位数表示回归线以下数据点的个数占总点数的比值。当分位数的值增加时，回归直线的斜率也在增大，降水的分布随气温的增加变得越来越宽。这说明在降水分布的不同位置，气温对降水的影响是不同的。所以在阿克苏河下游，多降水量的出现绝大多数情况是伴随着高温的；而在低气温时，多降水量的情况通常难以发生。这也是雨热同期的又一佐证。

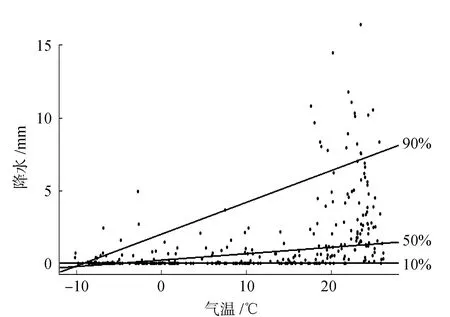
图6 降水与气温分位数回归图

3 结 论

本文选用阿克苏河下游阿拉尔站1980—2005年的逐月降水与气温资料，利用数据标准化、小波分析和小波相干法对两个气象数据序列进行了趋势、周期和一致性分析。

(1)26年间，阿克苏河下游降水呈减少趋势，减少率为0.01 mm/10 a；气温呈增加趋势，增加率为0.1 ℃/10 a。

(2)阿克苏河下游降水量的变化周期主要是0.5～1.0 a、4.0～8.0 a和16.0 a；阿克苏河下游气温的变化周期主要是1.0 a、2.0～4.0 a和8.0～16.0 a。

(3)阿克苏河下游在1 a的时间尺度上雨热同期。